Площадь дна сосуда s1
Асламазов Л. Гидростатика // Квант. – 1995. – № 1. – С. 51-55.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Давление и силы давления
Жидкость оказывает давление на стенки сосуда, в котором она находится, или на любую другую поверхность, соприкасающуюся с ней. Давление – величина скалярная. Оно измеряется абсолютной величиной нормальной (перпендикулярной поверхности) силы, действующей со стороны жидкости на единицу площади поверхности:
Давление в различных точках поверхности может быть разным. Поэтому площадь S мы должны брать достаточно маленькой.
По закону Паскаля давление жидкости не зависит от ориентации поверхности. Как бы ни была расположена поверхность в данном месте жидкости, давление на нее будет одним и тем же.
Сила давления всегда перпендикулярна поверхности. В обычных условиях она направлена так, как если бы жидкость стремилась расшириться.
Задача 1. В сосуд, имеющий форму куба с ребром a, налита доверху жидкость плотностью ρ. Определите силы давления жидкости на дно и стенки сосуда.
Давление жидкости на дно сосуда равно весу столба жидкости высотой a с площадью основания, равной единице: , где g – ускореннее свободного падения. (Для простоты здесь и в других задачах, где это специально не оговорено, предполагается, что атмосферное давление отсутствует). Сила давления на дно сосуда (рис. 1, а)
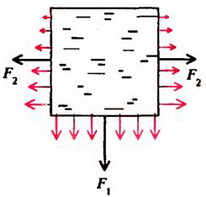
а
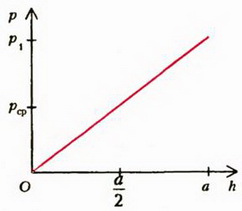
б
Рис. 1
Давление на боковую грань куба будет зависеть от расстояния до поверхности жидкости. На глубине h давление . Так как давление изменяется с глубиной по линейному закону (рис. 1. б), для определения силы давления мы должны среднее давление
умножить на площадь боковой грани
Задача 2. В цилиндрический сосуд диаметром D = 0,7 м вставлен поршень с длинной вертикальной трубкой диаметром d = 0,05 м (рис. 2). Максимальная сила трения между поршнем и стенками сосуда Fтp = 100 Н. Через трубку в сосуд наливают воду. При каком уровне воды в трубке H поршень начнет двигаться? Чему будет равна при этом сила давления воды на дно сосуда? Поршень расположен на высоте h = 0,2 м от дна сосуда. Плотность воды ρ = 103 кг/м3. Массой поршня с трубкой пренебречь.
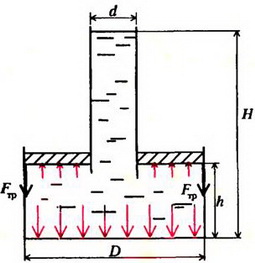
Рис. 2
Давление в жидкости на уровне поверхности поршня определяется расстоянием от этого уровня до свободной поверхности жидкости:
Поршень начнет двигаться, когда сила давления на него со стороны жидкости станет равной максимальной силе трения:
где – плошали поперечных сечений сосуда и трубки соответственно. Подставляя сюда выражение для p1, находим
Давление на дно сосуда .
Сила давления
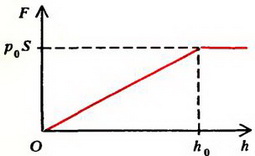
Задача 3. Длинная вертикальная труба с поршнем опущена одним концом в сосуд с водой. Вначале поршень находится у поверхности воды, затем его медленно поднимают. Как зависит сила, прикладываемая к поршню, от высоты h ее поднятия? Площадь поперечного сечения трубы S, атмосферное давление p0. Изменением уровня воды в сосуде, массой поршня и ею трением о стенки трубы пренебречь.
При поднятии поршня вода под действием атмосферного давления будет вначале заполнять трубу (рис 3, а). Давление в трубе на уровне жидкости в сосуде равно атмосферному давлению p0. Давление воды на поршень меньше атмосферного на величину веса столба жидкости высотой h и площадью основания, равной единице:
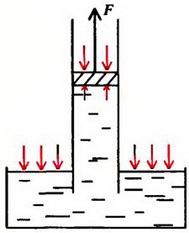
а
б
Рис. 3
Сверху на поршень по-прежнему действует атмосферное давление. Поэтому для удержания поршня на высоте h к нему надо приложить силу, равную
и направленную вверх.
С увеличением h давление воды на поршень будет уменьшаться. На высоте
давление обратится в ноль. При дальнейшем поднятии поршня уровень воды в трубе изменяться не будет, тан как сила атмосферного давления, действующая на столб жидкости в трубе снизу, уравновесится силой тяжести. Для удержания поршня на высоте h > h0 к нему надо приложить силу .
Зависимость прикладываемой к поршню силы F от высоты его поднятия h изображена графически на рисунке 3, б.
Высота столба воды в трубе , очевидно, может служить для измерения атмосферного давлении p0. Однако обычно в барометрах используют ртуть, и нормальному атмосферному давлению тогда соответствует значительно меньшая высота столба ртути = 0,76 м (плотность ртути ρрт = 1,36×104 кг/м3).
Примером другого гидростатического устройства, широко используемого в практике, являются сообщающиеся сосуды. Известен закон сообщающихся сосудов: если давление над жидкостью в сосудах одинаково, то уровни жидкости в них равны. Нетрудно доказать этот закон для случая цилиндрических сосудов (рис. 4). Так как жидкость в соединительной трубке находится в равновесии, то давления на нее с обеих сторон должны быть одинаковы. Поэтому равны и уровни жидкости в сосудах.
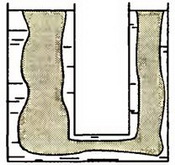
Рис. 4
В общем случае для доказательства закона сообщающихся сосудов можно воспользоваться принципом отвердевания, который часто используют в гидростатике. Суть этого принципа заключается в следующем: всегда можно представить себе, что часть жидкости отвердела – равновесие оставшейся части жидкости от этого не нарушится. Так, в цилиндрических сообщающихся сосудах мы можем мысленно выделить часть жидкости, которая заполняла бы сообщающиеся сосуды любой извилистой формы (см. рис. 4), и представить себе, что остальная часть жидкости отвердевает. Тогда равновесие выделенной нами части жидкости не нарушится, и, следовательно, уровни жидкости в извилистых сообщающихся сосудах будут такими же, какими были в цилиндрических сосудах, т.е. одинаковыми.
Закон сообщающихся сосудов справедлив только для однородной жидкости. Если в сосуды налиты жидкости разных плотностей, то уровни в сосудах могут быть разными.
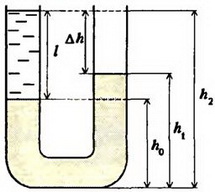
Задача 4. В U – образную трубку налита ртуть. Поверх ртути в одно из колен трубки налили воду (рис. 5, a). Высота столбика воды l = 0,1 м. Определите разность уровней жидкостей в коленах трубки. Нарисуйте график зависимости давления в обоих коленах трубки от высоты. Плотность ртути ρрт = 1,36×104 кг/м3, плотность воды ρрт = 103 кг/м3. Атмосферное давление не учитывайте.
а
б
Рис. 5
Давления на ртуть на уровне ho соприкосновения воды и ртути в обоих коленах должны быть одинаковы (закон сообщающихся сосудов для однородной жидкости). Поэтому
где разность уровней h2 – h1 обозначена через Δh. Отсюда
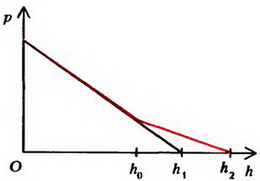
Давление в колене, содержащем только ртуть, меняется с высотой h по закону
Эта формула справедлива и в изогнутой части трубки. (Представите себе, что изогнутое колено сообщается с прямым цилиндрическим сосудом, в котором тоже находится ртуть. Тогда давления на одинаковой высоте в обоих сосудах должны быть равны). В другом колене в области , где находится только вода, давление
Ниже уровня h0 зависимость давления от высоты дается той же формулой, что и в первом колене:
Зависимость давления в коленах трубки от высоты изображена графически на рисунке 5, б. Как видно, выше уровня h0 давления на одинаковой высоте разные.
Выталкивающая сила
На тело, погруженное в жидкость, как известно, действует выталкивающая сила. Эта сила является равнодействующей сил давления жидкости на тело. Найдем, например, выталкивающую силу, действующую на кубик с ребром a целиком погруженный в жидкость плотностью ρ. Сила давления со стороны жидкости на верхнюю грань кубика равна
где h – расстояние от этой грани до поверхности жидкости (для простоты мы считаем, что плоскость верхней грани кубика параллельна поверхности жидкости). На нижнюю грань кубика действует сила
Силы давления на боковые грани кубика уравновешивают друг друга. Равнодействующая сил давлении, т.е. выталкивающая сила, равна
и направлена вертикально вверх. Мы получили закон Архимеда: выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость.
В общем случае закон Архимеда можно доказать с помощью принципа отвердевания. Мысленно заменим погруженное тело жидкостью. Очевидно, что эта жидкость будет находиться в равновесии. Следовательно, сила тяжести, действующая на нее, уравновешена силами давления со стороны окружающей жидкости. Если теперь представить себе, что выделенная нами часть отвердела, то равновесие оставшейся части не нарушится, и поэтому не изменятся силы давления на отвердевшую жидкость. Равнодействующая этих сил будет по-прежнему равна силе тяжести.
При доказательстве мы считали, что тело целиком погружено в жидкость. Однако аналогичные рассуждения легко провести и в случае, когда только часть тела находится в жидкости (проделайте это сами). И мы опять получим, что выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость:
где ρ – плотность жидкости, V – объем погруженной в жидкость части тела, g –ускорение свободного падения.
Задача 5. На дне водоема установлена П – образная конструкция из трех одинаковых балок, соединенных между собой (рис. 6). Как зависит сила давления этой конструкции на дно от уровня воды в водоеме? Рассмотрите два случая: 1) вода подтекает под опоры; 2) опоры плотно соприкасаются с дном. Балки имеют квадратное сечение со стороной a, длина балки l = 2a. Плотность материала балок ρ0. плотность воды ρ.
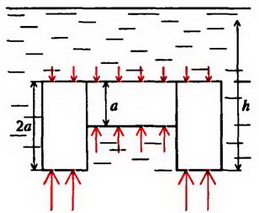
а
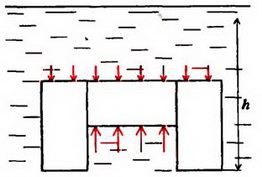
б
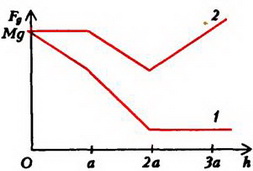
в
Рис. 6
Сила давления Fд на дно определяется разностью силы тяжести конструкции и выталкивающей силы F. В первом случае, когда вода подтекает под опоры (например, если дно водоема покрыто галькой – рисунок 6, а), справедлив закон Архимеда. Зависимость выталкивающей силы от высоты уровня воды h дается формулами:
Соответствующий график для силы Fд изображен на рисунке 6, в – он обозначен цифрой 1.
Во втором случае отсутствует давление воды на опоры снизу (рис.6, б), и пользоваться законом Архимеда уже нельзя. Для определения силы F необходимо найти равнодействующую сил давления:
F = 0 при h ≤ a,
Последнее выражение обращается в нуль при и при больших h становится отрицательным. Это означает, что при силы давления не выталкивают конструкцию из воды, а наоборот, прижимают ее ко дну. Зависимость силы давления на дно от высоты уровня воды показана на втором графике рисунка 6, в.
Задача 6. Пробковый кубик с ребром a = 0,1 м погрузили в воду на глубину h = 0,2 м с помощью тонкостенной трубки диаметром d = 0,05 м (рис. 7). Определите, какой груз надо положить в трубку, чтобы кубик от нее оторвался. Плотность пробки ρ0 = 200 кг/м3, плотность воды ρ = 103 кг/м3.
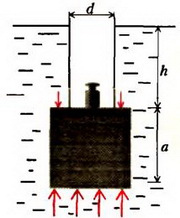
Рис. 7
Вес груза равен разности выталкивающей силы F действующей на кубик, и силы тяжести кубика . Если бы кубик был окружен со всех сторон водой, то на него по закону Архимеда действовала бы выталкивающая сила . В нашем случае выталкивающая сила будет большей, так как на часть поверхности верхней грани кубика, «заключенную» в трубку, не действует давление воды:
где – площадь сечения трубки. Таким образом, сила тяжести грузика
Масса грузика т = 1,2 кг.
Выталкивающую силу, действующую на кубик, можно найти и другим способом. Рассмотрим кубик с трубкой как единое тело, вытесняющее объем воды
Тогда по закону Архимеда на кубик с трубкой действует выталкивающая сила
которая равна выталкивающей силе, действующей на кубик, так как равнодействующая сил давления воды на трубку равна нулю.
Жидкость в движущемся сосуде
Изучим теперь равновесие жидкости в сосуде, движущемся с ускорением. По второму закону Ньютона в этом случае векторная сумма всех сил, действующих на любой выделенный элемент жидкости, должна равняться , где m – масса выделенной жидкости,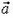 
– ускорение сосуда. Но на выделенный элемент жидкости действуют сила тяжести и силы давления со стороны окружающей жидкости. Их равнодействующая и должна быть равна .
Задача 7. Сосуд с жидкостью плотностью ρ падает с ускорением a. Определите давление жидкости на глубине h и силу давления на дно сосуда. Высота уровня воды в сосуде H, площадь дна сосуда s.
Выделим столбик жидкости высотой h с площадью основания s. На него действуют сила тяжести и сила давления , направленная вверх. Равнодействующая этик сил создает ускорение столбика:
где – масса столбика. Для давления p на глубине h отсюда находим
Сила давления на дно сосуда
будет тем меньше, чем больше ускорение сосуда a. При (свободное падение) сила давления жидкости обращается в ноль – наступает состояние невесомости. При жидкость будет свободно падать с ускорением g, а сосуд – с большим ускорением, и вода вытечет из сосуда.
Задача 8. На дне сосуда с жидкостью лежит тело. Может ли тело всплыть, если сосуд начнет двигаться вверх с ускорением? Определите силу давления тела на дно сосуда, если ускорение сосуда a, плотность жидкости ρ0, плотность тела ρ, его объем V.
На тело, лежащее на дне сосуда, действуют сила тяжести mg сила реакции дна N и выталкивающая сила F (рис. 8). Если сосуд покоится, то сумма этих сил равняется нулю. При движении сосуда с ускорением a вверх по второму закону Ньютона имеем
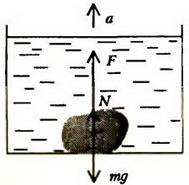
Рис. 8
Определим выталкивающую силу F. Аналогично решению предыдущей задачи, легко получить, что при ускоренном движении сосуда, вверх давление на глубине h дается формулой
т.е. давление в раз больше, чем в неподвижном сосуде. Соответственно будет большей и выталкивающая сила:
где – масса вытесненной телом воды.
Подставляя это выражение в формулу второго закона Ньютона, для силы реакции дна получаем
Легко видеть, что в сосуде, движущемся с ускорением вверх, сила реакции дна всегда больше, чем в неподвижном. Поэтому тело не только не всплывает, а наоборот, сильнее прижимается ко дну.
Задача 9. Сосуд с жидкостью движется горизонтально с ускорением a. Определите форму поверхности жидкости в сосуде.
Выделим горизонтальный столбик жидкости длиной l и площадью поперечного сечения S (рис. 9). По второму закону Ньютона
где – масса столбика, p1 и p2 – давления на него слева и справа.
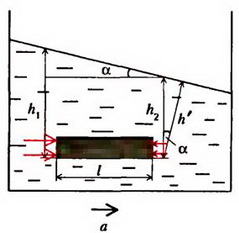
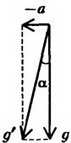
Рис. 9
Давление на глубине h определяется по обычной формуле (по вертикали ускорения нет). Подставляя выражения для m и p в уравнение второго закона Ньютона, получаем
или
Но – это разность высот точек поверхности жидкости. Мы получаем, что поверхность жидкости – плоскость, наклоненная к горизонту под углом α, причем .
Заметим, что давление жидкости на данной высоте здесь не одно и то же. Линии равного давления параллельны поверхности жидкости. Если ввести расстояние h´ от точки до поверхности жидкости, то давление в этой точке
Поэтому можно сказать, что ускоренное движение сосуда эквивалентно замене ускорения свободного падения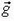 
на величину . Это утверждение в равной степени относится и к предыдущим двум задачам.
Упражнения
1. Три сосуда, имеющие формы цилиндра, усеченного конуса и перевернутого усеченного конус с одинаковыми площадями оснований и рапными объемами, доверху наполнены водой. Как соотносятся между собой силы давлении воды на дно сосудов?
2. Трубка ртутного барометра подвешена нити. Определите натяжение нити, если высота уровня ртути и трубке Н = 0,76 м, внешний диаметр трубки D = 0,02 м, внутренний d = 0,017 м. нижний конец трубки погружен в ртуть на глубину h = 0,1 м, масса трубки m = 0,3 кг, плотность ртути ρ = 1,36×104 кг/м4. Считайте, что торцы трубки плоские.
3. Длинная вертикальная трубка погружена одним концом в сосуд с ртутью. В трубку наливают m = 0,71 кг воды, которая не вытекает из трубки. Определите изменение уровня ртути и сосуде. Диаметр сосуда D = 0,06 м, плотность ртути ρ = 1,36×104 кг/м4. Толщиной стоим трубки пренебречь.
4. В сосуде с водой плавает кусок льда. Изменится ли уровень воды в сосуде, если лед растает? Что будет, если в лед вморожен а) кусочек свинца: б) кусочек пробки?
5. В цилиндрические сообщающиеся сосуды диаметрами D = 0,06 м и d = 0,02 м налита вода. Как изменятся уровни воды в сосудах, если в один из сосудов поместить тело массой т = 0,02 кг, которое будет плавать в воде? Плотность воды ρ = 103 кг/м3.
6. Сосуд с водой скользит без трения по наклонной плоскости с углом наклона α. Определите, как расположится поверхность воды и сосуде.
Ответы
1. Сила давления на дно наибольшая у сосуда, имеющего форму усеченного конуса, наименьшая – у перевернутого конуса.
2.
3.
4. Если лед чистый или в него вморожен кусочек пробки, то уровень воды не изменится. Если же в лед вморожен кусочек свинца, уровень воды понизится.
5.
6. Поверхность параллельна наклонной плоскости.
Источник
Тема. Решение задач по теме “Гидростатика и гидродинамика”.
Цели:
- – рассмотреть основные приемы решения расчетных задач на тему “Гидростатика и гидродинамика”.
Ход занятия
В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач.
Прежде чем приступить к выполнению задания, следует повторить основные законы гидромеханики.
Основной закон гидростатики – закон Паскаля, согласно которому в состоянии равновесия давление жидкости в данной точке не зависит от ориентации площадки, на которую она действует.
Поскольку в школьном курсе рассматривается стационарное течение несжимаемой жидкости, то будет справедливо уравнение неразрывности струи.
Для идеальной жидкости выполняется уравнение Бернулли. Покажите, что уравнение Бернулли является следствием закона сохранения энергии.
Качественные задачи
- К концам равноплечного рычага подвесили две одинаковые гири. Что произойдет, если одну гирю поместить в воду, а другую в керосин?
Ответ: равновесие нарушится.
- Почему, если близко стоишь около быстро идущего поезда, возникает эффект “притягивания” к колесам?
Ответ: проходящий поезд увлекает за собой примыкающие к нему слои воздуха. Воздух, движущийся между человеком и поездом, оказывает на него меньшее давление, чем неподвижный. Эта разность давлений и обусловливает силу, увлекающую человека к поезду.
- При испытании реактивного снаряда, установленного в хвосте самолета для защиты его от нападения сзади, был обнаружен удивительный факт: при пуске снаряд разворачивался и догонял свой самолет. Как можно объяснить это явление?
- Проделайте эксперимент. Вложите в воронку бумажный фильтр (рис. 1) и попробуйте выдуть его через узкий конец воронки. У вас не получилось? Почему?
Ответ: чем сильнее вы вдуваете воздух, тем плотнее фильтр входит в воронку. Объясняется это с помощью закона Бернулли, согласно которому давление понижается в местах сужения. В узком просвете между воронкой и бумажным фильтром давление понижается, и внешнее атмосферное давление удерживает фильтр в воронке.
Примеры решения расчетных задач
Задача 1. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S1, сечение струи S2 (рис. 2). Найдите ускорение, с которым перемещается уровень воды в сосуде.
Решение:
Будем считать жидкость несжимаемой. Тогда для каждого момента времени, согласно уравнению неразрывности струи, можно записать
S1v1 = S2v2, (1)
где v1 – скорость воды в сосуде, v2 – скорость воды в струе вблизи отверстия.
Возьмем производную по времени от (1)
,
где – ускорение воды в сосуде, – ускорение свободного падения, так на выходе из сосуда вода начинает свободно падать. Таким образом,
.
Ответ: .
Задача 2. В сосуде с жидкостью сделано отверстие площадью S. Размеры отверстия малы по сравнению с высотой столба жидкости. В одном случае отверстие закрыто пластинкой и измеряется сила давления жидкости на пластинку F1 при высоте столба жидкости h (рис. 3). В другом случае тот же сосуд стоит на тележке, отверстие открыто, и измеряется сила отдачи F2 при установившемся токе жидкости в момент, когда высота столба жидкости будет та же, что и в первом случае. Будут ли силы F1 и F2 равны?
Решение:
Согласно закону Паскаля давление на жидкость передается во всех направлениях одинаково, поэтому в первом случае давление, производимое на пластинку жидкостью, равно гидростатическому давлению столба жидкости высотой h, а значит, F1 = ρghS , где ρ – плотность жидкости.
Во втором случае сила F2 согласно второму закону Ньютона равна изменению импульса жидкости в единицу времени
.
Изменение импульса Δp = Δmv , где Δm – масса жидкости, вытекающей в единицу времени, v – скорость истечения жидкости из отверстия.
Масса вытекающей жидкости Δm = ρgS, скорость истечения согласно формуле Торричелли . Следовательно,
F2 = ρv2S = 2ρghS.
Таким образом, F2 = 2F1 . Объяснить это можно так. Когда жидкость вытекает из малого отверстия, линии тока вблизи него сгущаются, а значит, как следует из уравнения Бернулли, давление на стенку вблизи отверстия уменьшается. Поэтому сила реакции вытекающей струи оказывается больше силы статического давления на площадь отверстия.
Ответ: силы F1 и F2 не равны.
Задача 3. Из крана выливается вода. Начиная с некоторого места, диаметр струи уменьшается на протяжении h от а до b (рис. 3). Сколько воды вытечет из крана за время t?
Решение:
Воспользуемся условием стационарности течения несжимаемой жидкости
. (1)
Для идеальной жидкости справедливо уравнение Бернулли:
.
Поскольку жидкость свободно падает, то давления в обоих сечениях одинаковы, и уравнение Бернулли принимает вид:
. (2)
За время t через любое сечение протекает один и тот же объем воды, поэтому можно записать
. (3)
Выразим скорость v1 из (1) и (2):
.
Подставим полученное значение v1 в (3) и получим окончательный ответ:
.
Ответ: .
Задача 4. Площадь поршня в шприце S1 = 2 см2, а площадь отверстия S2 = 1 мм2 (рис. 4). Сколько времени будет вытекать вода из шприца, если действовать на поршень с силой F = 5 H и если ход поршня l = 5 см?
Решение:
Так как из шприца вытечет вся находившаяся в нем жидкость, то
S1l = S2v2t, (5)
где v2 – скорость истечения струи. Будем считать жидкость идеальной, тогда можно использовать уравнение Бернулли:
.
Шприц расположен горизонтально, следовательно, h = const. Уравнение Бернулли тогда запишется следующим образом:
, (6)
где Ра – атмосферное давление, а v1 – скорость движения поршня. Из уравнения неразрывности следует
S1v1 = S2v2. (7)
Решая совместно уравнения (6) и (7), получим
,
отсюда
.
Подставляя найденное значение v2 в (5), получим
.
Так как S2S1 , то можно записать
.
Ответ:
Задачи для самостоятельной работы
- “Вечерело. Уставший за нелегкий трудовой день Абдулла Ибн Сауд присел на берегу реки и стал обдумывать свой социальный статус. В колхоз не берут, кооперативы эмир разогнал, к нему самому на службу устраиваться – так стражники без золотых во дворец не пускают. Эх, жизнь… Но тут взгляд Абдуллы остановился: по реке плыл какой-то предмет, и лишь маленький кусочек сургуча был виден над водой. Абдулла бросился в воду и вытащил оттуда старинный глиняный кувшин, герметично закупоренный сургучом. Распечатав кувшин и перевернув его, Абдулла обомлел: сверкнуло золото. Из кувшина высыпалось 147 одинаковых золотых монет. Монеты Абдулла спрятал, а сосуд запечатал и бросил обратно в воду. Поплыл сосуд дальше, примерно треть его объема торчало над водой”.
Так говорится в одной из восточных сказок. Предполагая, что кувшин был двухлитровый, оцените массу одной золотой монеты.Ответ: m = 4,45 г.
- На некоторых железных дорогах пополнение паровозного котла водой производится без остановки паровоза. Для этой цели применяется изогнутая под прямым углом труба, которая опускается на ходу паровоза в канаву с водой, проложенную вдоль рельсов. При какой скорости паровоза вода может подняться на высоту 3 м?
Ответ: v = 28 км/ч.
- Из поднятого на высоту h резервуара выходит труба постоянного сечения S, переходящая в короткую трубу сечением S1, перекрытую краном. Найдите давление в магистральной трубе при открытом кране.
Ответ: Р = Ратм + ρgh.
- Определите расход воды Q, протекающей через слив плотины, имеющей ширину l, глубину потока d и понижение уровня потока по сравнению с уровнем воды в водохранилище, равное h.
Ответ: Q = ρdl·√(2gh).
- Какова примерно скорость катера, если при его движении вода поднимается вдоль его носовой части
на высоту h = 1 м?Ответ: v ≈ √(2gh) ≈ 4,4 м/с.
- На гладкой горизонтальной поверхности стоит цилиндрический сосуд с водой. В боковой стене сосуда у дна имеется отверстие площадью S0. Какую силу нужно приложить к сосуду в горизонтальном направлении, чтобы удержать его в равновесии? Площадь поперечного сечения сосуда равна S, высота столба жидкости h.
Ответ: .
- На поршень шприца площади S действует сила F. С какой скоростью v должна вытекать в горизонтальном направлении струя из отверстия иглы площади s? Плотность жидкости ρ. Трением пренебречь.
Ответ: . Если s S, то .
Рекомендуемая литература
- Бутиков Е.И., Кондратьев А.С. Физика. Т. 1. Механика. – М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. – С. 332-352.
- Физика. Механика / Под ред. Г.Я. Мякишева. – М.: Просвещение, 1995. – С. 420-436.
- Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. – М.: Физматлит, 2005. – С. 63-67.
- Готовцев В.В. Лучшие задачи по механике и термодинамике. – М.; Ростов н/Д: Издательский центр “Март”, 2004. – С. 184-212.
Источник