Почему при расширении газа в открытом сосуде произойдет

Процесс адиабатного расширения сжатого газа сопровождается снижением температуры. Связь между давлением и температурой для идеального газа в адиабатном процессе выражается соотношением
где k — показатель адиабаты.
В адиабатном процессе расширения теплообмен с окружающей средой отсутствует, поэтому вся внутренняя энергия полностью преобразуется в механическую работу. При расширении реального газа затрачивается дополнительная работа на преодоление внутренних сил притяжения его молекул и выполнение внешней работы.
Если воздух, сжатый до 9,5 МПа при t{ = 20°С, адиабатно расширяется до 0,1 МПа, то при k = 1,4 его конечная температура t2 = -193,4°С.
Принудительное расширение газов, сопровождающееся понижением их температуры, осуществляется в расширительных машинах — поршневых детандерах и турбодетандерах (рис. 18.1).
Рис. 18.1. Схемы детандирования в поршневом детандере (а) и турбодетандере (б)
Изменение энтальпии (без учета потерь и подвода теплоты) при детан- дировании
где tjv — адиабатный КПД детандера; для поршневых детандеров ц5 = = 0,7-^0,9, для турбодетандеров r|s= 0,65-^0,87.
Процессы детандирования широко применяются в криогенной технике и относительно редко — в холодильной.
Охлаждение с помощью дросселирования. Дросселированием называется снижение давления жидкости или газа при проходе через любое суженное отверстие (диафрагму, клапан). При быстром снижении давления внешняя работа не совершается и теплообмена с внешней средой практически не происходит. Энтальпия в этом процессе не изменяется, а энтропия возрастает из-за расхода внутренней энергии потока на преодоление трения, что указывает на необратимость процесса.
За суженным отверстием в зависимости от свойств и состояния реального газа внутренняя энергия может быть больше или меньше внутренней энергии до суженного отверстия либо равна ей. В зависимости от характера изменения внутренней энергии конечная температура реального газа может быть выше или ниже начальной температуры либо равна ей.
Изменение температуры вещества при дросселировании называется эффектом Джоуля — Томпсона, его применяют в технике глубокого охлаждения реальных газов. Дросселирование жидкости сопровождается значительным снижением температуры. Это вызвано тем, что при дросселировании жидкости (особенно насыщенной) происходит парообразование в результате превращения работы сил трения в теплоту и передачи ее жидкости. При этом увеличивается объем и совершается большая работа по преодолению сил взаимного притяжения молекул. Если теплообмен с окружающей средой отсутствует, работа по преодолению сил притяжения будет сопровождаться уменьшением внутренней энергии, а следовательно, и температуры парожидкостной смеси. Процесс дросселирования жидкости широко используется для получения умеренно низких температур.
Вихревой эффект охлаждения. Охлаждение воздуха этим способом основано на эффекте Ранка — Хилъша1 и осуществляется с помощью вихревой грубы.
Конструкция вихревой трубы, в которой происходит температурное разделение потока воздуха, достаточно проста (рис. 18.2). Воздух при давлении 0,3—0,5 МПа и температуре окружающей среды поступает в цилиндрическую трубу III через сопло I но касательной к внутренней поверхности трубы. Воздух, поступая в трубу, совершает вращательное движение, одновременно перемещаясь от сопла I к дросселю II. При этом воздушный поток, выходя из сопла по касательной к внутренней поверхности трубы, образует свободный вихрь. Его угловая скорость велика около оси и уменьшается но мере удаления от нес.
Рис. 18.2. Схемы вихревых труб:
а — прямоточная; б — противоточная; I — сопло; II — дроссель; III — цилиндрическая труба;
IV — диафрагма
В процессе движения воздуха к дроссельному клапану II угловая скорость между слоями потока выравнивается вследствие трения между ними (скорость внутренних слоев снижается, внешних – возрастает), при этом кинетическая энергия внутренних слоев передается периферийным слоям. В результате наружные слои воздуха оказываются более нагретыми, внутренние — холодными, т.е. через диафрагму IV (или трубу меньшего диаметра) выходит холодный воздух, а через дроссель II по периферии трубы III — горячий. Температура холодного воздуха на 30—70°С ниже начальной температуры воздуха, выходящего из сопла.
В вихревой камере температурное расслоение воздуха происходит значительно быстрее, чем установление термического равновесия. При давлении воздуха 0,3—0,5 МПа образуется холодный поток температурой 10—50°С и горячий — температурой 100— 130°С.
Хотя большие необратимые потери при расширении воздуха в вихревой трубе предопределяют сравнительно большие энергетические затраты, которые значительно превышают затраты при изоэнтропном расширении с совершением внешней работы, не всегда результат энергетического сопоставления может быть решающим при оценке холодильных систем.
1 Эффект Ранка — Хильша — эффект разделения газа или жидкости при закручивании в цилиндрической или конической камере на две фракции.
При периодической потребности в охлаждении на различных предприятиях при необходимости малой холодопроизводительности выгоднее применять простую и надежную вихревую трубу, поскольку исключительная простота и надежность вихревой трубы делают ее в некоторых случаях более предпочтительной.
Источник
Стасенко А.Л. Расширение газа в пустоту //Квант. — 1987. — № 11. — С. 38-39.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Спросите кого угодно, что произойдет с температурой идеального газа, который расширяется в замкнутом сосуде без теплообмена с окружающей средой, и почти все вам ответят, что газ охладится. Не «верьте! Это не всегда так.
Вообразим такой мысленный эксперимент. Пусть одна половина теплоизолированного сосуда занята идеальным газом с давлением p1 и температурой T1, а другая — пуста (рис. 1). В некоторый момент уберем перегородку между половинами сосуда. Газ, естественно, будет расширяться, причем в пустоту, и после многочисленных столкновений его молекул со стенками и между собой установится новое равновесное состояние. Ясно, что теперь объем газа вдвое больше: V2 = 2V1. А каковы его давление p2 и температура T2?

Рис. 1
С одной стороны, так как процесс адиабатический, точки, соответствующие начальному и конечному состояниям газа, должны лежать на адиабате 1—2’ (рис. 2). Адиабата, как известно, падает круче изотермы, поэтому температура газа должна уменьшаться: T’2 < T1.
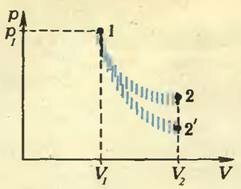
Рис. 2
С другой стороны, посмотрим, что говорит первый закон термодинамики. Количество теплоты Q, подведенное к газу, идет на увеличение его внутренней энергии ΔU и на работу по расширению А:
(~Q = Delta U + A) .
В нашем случае Q = 0 (по условию адиабатичности). А какая работа совершается газом? Да никакой, потому, что он расширяется в вакуум, со стороны которого не встречает противодействия. Значит, и сила, и работа равны нулю: А = 0. Следовательно, и изменение внутренней энергии тоже равно нулю: ΔU = 0. Но поскольку в случае идеального газа внутренняя энергия зависит только от температуры, температура не изменится: T2 = T1, и давление станет равным (~p_2 = frac{p_1}{2}). Это означает, что точки, соответствующие начальному и конечному состояниям, будут лежать на изотерме 1–2.
А что происходит между этими состояниями? К сожалению, школьная термодинамика ничего об этом сказать не может. Почему? Да потому, что вся она верна только для очень медленных (так называемых квазистатических) процессов, которые происходят со скоростями, много меньшими тепловой скорости движения молекул. В нашем же случае как только мы уберем перегородку, газ буквально бросится в вакуум со скоростью порядка тепловой скорости молекул и даже еще быстрее, потому что в газе есть отдельные молекулы, скорость которых намного больше тепловой. А тут термодинамика просто неверна. Вот почему на рисунке 2 мы изобразили неизвестный нам процесс штрихами, а не сплошной линией.
Все наши рассуждения справедливы для случая идеального газа. А если газ не идеальный? Тогда его молекулы взаимодействуют друг с другом, и внутренняя энергия газа складывается из кинетической энергии движения молекул и потенциальной энергии их взаимодействия.
На рисунке 3 изображена зависимость потенциальной энергии П взаимодействия двух молекул от расстояния r между ними. Там, где потенциальная энергия минимальна (точка r0), вещество конденсируется, т. е. переходит в жидкое состояние.
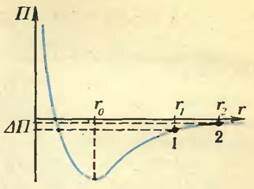
Рис. 3
Так как, по условию, мы имеем в начальный момент газ, то среднее расстояние между молекулами соответствует точке r1 >> r0. После удвоения объема среднее расстояние между молекулами станет равным (~r_2 = r_1 sqrt[3]{2} > r_1). Получилось, как будто в результате расширения газ слегка «вытащили» наверх, по склону потенциальной ямы. Но кто поработал над тем, чтобы увеличить потенциальную энергию на ΔП? Никто. И сам газ тоже ни над кем не работал. Поэтому остается признать, что увеличение потенциальной энергии произошло за счет уменьшения кинетической энергии движущихся молекул. Значит, и температура — мера средней кинетической энергии молекул газа — в результате расширения слегка упадет. Но это верно только в случае реального газа.
Источник
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние (рис. 1).

Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма . С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу . Тогда работа газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу , которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой , равной силе по модулю и противоположной по направлению: (рис. 4).

Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем: , или .
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Источник
Изопроцессы
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:
• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;
• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).
Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.
Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.
Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .
Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.
Изотермический процесс
Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.
Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:
Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.
Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:
Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:
Данное утверждение называется законом Бойля — Мариотта.
Записав закон Бойля — Мариотта в виде
можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.
Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.
Графики изотермического процесса
Вообще, графики термодинамических процессов принято изображать в следующих системах координат:
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат .
График изотермического процесса называется изотермой.
Изотерма на -диаграмме — это график обратно пропорциональной зависимости .
Такой график является гиперболой (вспомните алгебру — график функции ). Изотерма-гипербола изображена на рис. 1 .
Рис. 1. Изотерма на -диаграмме
Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на —диаграмме.
В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2 ). Первый процесс идёт при температуре , второй — при температуре .
Рис. 2. Чем выше температура, тем выше изотерма
Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление , на второй — p_1′ alt=’p_2 > p_1′/> . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, T_1′ alt=’T_2 > T_1′/> .
В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3 ):
Рис. 3. Изотермы на и -диаграммах
Изобарный процесс
Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.
Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно
где — атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .
Выпишем уравнения состояния:
Поделив их друг на друга, получим:
В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:
Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.
Графики изобарного процесса
График изобарного процесса называется изобарой. На -диаграмме изобара является прямой линией (рис. 4 ):
Рис. 4. Изобара на -диаграмме
Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.
Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на —диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и (рис. 5 ):
Рис. 5. Чем ниже изобара, тем больше давление
Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).
Стало быть, p_1′ alt=’p_2 > p_1′/> .
В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6 ):
Рис. 6. Изобары на и -диаграммах
Изохорный процесс
Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и . Имеем:
Делим эти уравнения друг на друга:
Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
Ввиду произвольности выбора состояний мы приходим к закону Шарля:
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:
Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.
Графики изохорного процесса
График изохорного процесса называется изохорой. На -диаграмме изохора является прямой линией (рис. 7 ):
Рис. 7. Изохора на -диаграмме
Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.
Далее, чем больше объём, тем ниже идёт изохора на —диаграмме (рис. 8 ):
Рис. 8. Чем ниже изохора, тем больше объём
Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, V_1′ alt=’V_2 > V_1′/> .
В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9 ):
Рис. 9. Изохоры на и -диаграммах
Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.
Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
Источник
Как изменяется давление газа при изотермическом расширении
Одним из основных термодинамических процессов, совершающихся в большинстве тепловых машин, является процесс расширения газа с совершением работы. Легко определить работу, совершаемую при изобарном расширении газа.
Если при изобарном расширении газа от объема V1 до объема V2 происходит перемещение поршня в цилиндре на расстояние l (рис. 7.3), то работа A’, совершенная газом, равна
, (7.27)
где p — давление газа,
— изменение его объема.
3
Как видно из рисунка 7.4, при изображении изобарного процесса расширения газа в координатных осях p , V площадь фигуры, ограниченной графиком процесса, координатами V1 и V2, осью абсцисс, пропорциональна работе газа A’.
Работа при произвольном процессе расширения газа. Произвольный процесс расширения газа от объема V1 до объема V2 можно представить как совокупность чередующихся изобарных и изохорных процессов.
При изохорных процессах работа равна нулю, так как поршень в цилиндре не перемещается. Работа при изобарных процессах пропорциональна площади фигуры на диаграмме p, V под соответствующим участком изобары (рис. 7.5).
Следовательно, работа при произвольном процессе расширения газа прямо пропорциональна площади фигуры под соответствующим участком графика процесса на диаграмме p, V.
Работа при изотермическом расширении газа. Сравнивая площади фигур под участками изотермы и изобары (рис. 7.6), можно сделать вывод, что расширение газа от объема V1 до объема V2 при одинаковом начальном значении давления газа сопровождается в случае изобарного расширения совершением большей работы.
Сейчас для нас важно свойство натуральных логарифмов, выраженное соотношением (14). Мы можем заменить очень маленькое число х натуральным логарифмом от (1+х) и наоборот. Такая подстановка оказывается очень полезной в выражении (7), которое мы для удобства выпишем здесь еще раз:
Вспомним, что
есть очень малое приращение V. Поэтому члены — очень малые числа, и мы можем заменить их логарифмами, согласно (14). Таким образом,
Последний шаг требует некоторого пояснения. Мы получили, что отношение dV/V, которое представляет собой просто очень малое относительное изменение V, равно d(ln V), т. е. очень малому изменению или дифференциалу натурального логарифма V. Подумав, можно понять, что это следует из последнего равенства в (15), которое дает разность натурального логарифма от (V + dV) и натурального логарифма от V% т. е. изменение величины натурального логарифма V при переходе от V к V+dV. Мы обозначили это малое изменение как дифференциал
. Подставив вместо каждого из членов dV/V в (7), получим
Таким образом, работу, выполненную идеальным газом, расширяющимся при постоянной температуре, легко подсчитать, взяв натуральный логарифм отношения конечного объема к начальному и умножив его на nRT, где n — число молей газа, R — газовая постоянная и Т — абсолютная температура.
Основной результат этого длинного и несколько запутанного упражнения можно записать в виде
Рис. 4.5. Один из способов осуществления работы с помощью процесса изотермического расширения.
Тот же результат должен быть справедлив для любой другой переменной, например p или Т:
Интегралы такого типа будут встречаться нам в дальнейшем. Полезно запомнить следующее соотношение, где х означает любую переменную:
Закончим это обсуждение вычислением величины работы при изотермическом расширении. Пусть имеется цилиндр с поршнем, погруженный в сосуд с кипящей водой, так что поддерживается температура 373 К. В цилиндре находится 1 моль газа. В начальный момент сила давления газа, приложенная к поршню и направленная вверх, достаточна, чтобы поддерживать на данном уровне поршень и стоящий на нем открытый сосуд с водой (рис. 4.5). По мере испарения воды из сосуда направленная вниз сила тяжести, действующая на поршень и сосуд, будет уменьшаться, и поршень начнет подниматься. Примем, что он поднимается до тех пор, пока объем газа в цилиндре не станет вдвое больше первоначального. Согласно (16), имеем
Заметим, что ответ не зависит от того, каковы фактические значения начального и конечного объемов, а зависит только от их отношения. Та же самая работа будет произведена, если увеличить массу поршня и сосуда настолько, чтобы начальный и конечный объемы уменьшились вдвое при прежнем количестве газа. Давление тогда возросло бы вдвое. Если удвоить начальный объем газа при неизменном его количестве, то при данной температуре он совершит одну и ту же работу независимо от давления. Заметим, что эти утверждения справедливы только для идеального газа, подчиняющегося уравнению состояния pV = nRT. Для других уравнений состояния вычисление
основано на тех же принципах, но немного более сложно.
Интересно сравнить величину работы при изотермическом расширении с величиной работы расширения газа при постоянном давлении. Процесс расширения при постоянном давлении можно осуществить, например, если вынуть цилиндр из сосуда с кипящей водой и поставить его на плитку. По мере нагревания газа он будет расширяться. Если сосуд с водой, стоящий на поршне, накрыть крышкой, то масса будет оставаться постоянной, а поршень будет медленно подниматься, по мере того как объем газа будет увеличиваться при постоянном давлении. Из выражения (4) получаем выражение для работы, совершаемой при удвоении объема:
В процессе расширения при постоянном давлении газ совершает почти в 1,5 раза больше работы, чем в процессе при постоянной температуре. Дополнительная работа идет на поднятие воды, которая при изотермическом расширении испарялась.
В сосуде под поршнем находится 3 моля гелия. Что произойдет с давлением газа на стенки сосуда, температурой и объемом газа при его изотермическом расширении?
К каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.
Б) Температура газа
Изотермическим называется процесс при постоянной температуре. Следовательно, температура газа останется неизменной (Б — 3). Поскольку газ расширяется в сосуде, его объем увеличивается (В — 1). Гелий является инертным газом, поэтому его можно считать идеальным. При изотермическом процессе, согласно закону Бойля-Мариотта, величина
остается постоянной. Таким образом, заключаем, что при изотермическом расширении гелия в сосуде его давление уменьшается (А — 2).
Источник
Источник
