| |
|
, , (1643) , ( (1)) : [v = sqrt {2gh} ,] (h) − , (g) − . 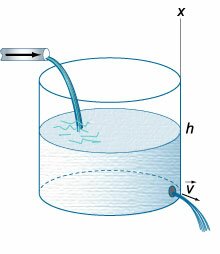
| | .1 | .2 |
, (h) . , . , . , (varphi:) [v = varphisqrt {2gh} ,] (varphi) (1.) (varphi) . ( (2)) . , . , [v = kh,] (k) − , , . ( ). , . , , , (R.) , (a) ( (3)). 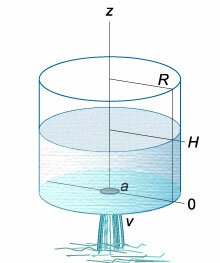
| 
| .3 | .4 |
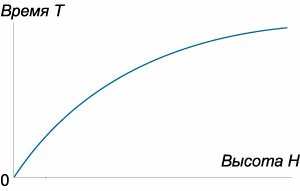
: [v = sqrt {2gz} ,] (z) − . : [q = – pi {a^2}sqrt {2gz} .] (pi {a^2}) , , “” , . : [frac{{dV}}{{dt}} = q.] (dV) [dV = Sleft( z right)dz,] [frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).] (qleft( z right)) : [frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .] ({Sleft( z right)}) (z) [Sleft( z right) = pi {R^2},] (R) − . [require{cancel} cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} . ] : [frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.] , , (H,) (T) (0:) [ {intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};; {Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};; {Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};; {Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.} ] (T:) [T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .] , (a = R) ( ), (T = sqrt {largefrac{{2H}}{g}normalsize}, ) (H.) (T) (H) (4.) . | 1 | |
(T.) (R,) (a.) (H) ( (5)). 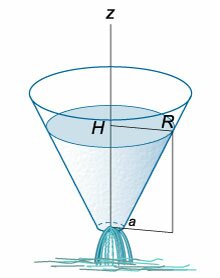
| | .5 | .6 |
(z) [Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),] (Sleft( z right)) − (z,) (qleft( z right)) − , (z.) , , . , : [qleft( z right) = – pi {a^2}sqrt {2gz} ,] (a) − . , , ( (6) ). , [frac{R}{H} = frac{r}{z}.] , (z) [ {Sleft( z right) = pi {r^2} } = {pi {left( {frac{{Rz}}{H}} right)^2} } = {frac{{pi {R^2}{z^2}}}{{{H^2}}}.} ] (Sleft( z right)) (qleft( z right)) , : [frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .] : [{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.] , , (H) (T:) [ {intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};; {Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};; {Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};; {Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};; {Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .} ] (H) . , : [T = sqrt {frac{{2H}}{g}}. ] , , (H, R) (a) (5) , ( (3) !). , ? | 2 | |
(R) (H,) . 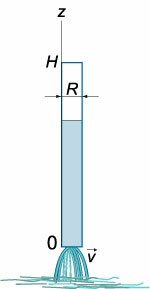
| 
| .7 | .8 |
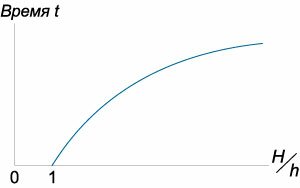
, (z) : [Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).] (Sleft( z right)) : [Sleft( z right) = S = pi {R^2},] , , : [qleft( z right) = – kz,] (k) , . : [pi {R^2}frac{{dz}}{{dt}} = – kz,] : [frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.] , , (H) (h) (0) (t:) [ {intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};; {Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};; {Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.} ] (t) (largefrac{H}{h}normalsize) (8.) (T) (H) , . , (t) (h to 0.) | |
|

