Почему вода не вытекает из сосуда

Закон Торричелли
Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
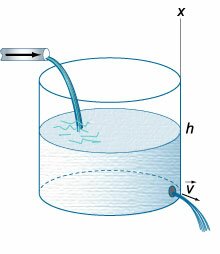
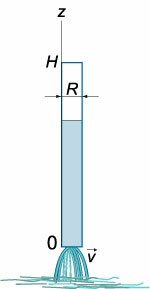
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:
[v = sqrt {2gh} ,]
где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
| |
Рис.1 | Рис.2 |
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.
В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)
[v = varphisqrt {2gh} ,]
где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.
Вытекание жидкости из тонкой трубки
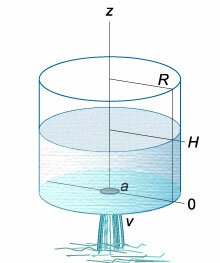
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.
Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть
[v = kh,]
где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.
Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).
Дифференциальное уравнение вытекания жидкости
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
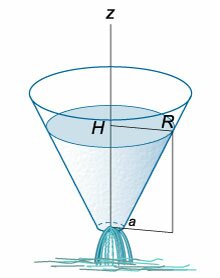
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
|
|
Рис.3 | Рис.4 |
Скорость жидкости описывается формулой Торричелли:
[v = sqrt {2gz} ,]
где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:
[q = – pi {a^2}sqrt {2gz} .]
Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.
Уравнение баланса жидкости в резервуаре описывается следующим образом:
[frac{{dV}}{{dt}} = q.]
Поскольку изменение объема (dV) можно выразить как
[dV = Sleft( z right)dz,]
то мы получаем дифференциальное уравнение
[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]
Подставим функцию (qleft( z right)) в это уравнение:
[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно
[Sleft( z right) = pi {R^2},]
где (R) − радиус основания цилиндра. Тогда
[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]
В результате получаем уравнение с разделяющимися переменными:
[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]
Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)
[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]
Отсюда следует выражение для полного времени вытекания жидкости (T:)
[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]
Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
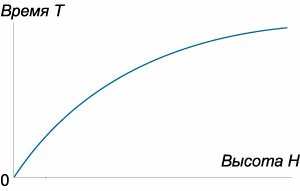
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)
Аналогично можно описать вытекание жидкости и из сосуда другой формы.
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
| |
Рис.5 | Рис.6 |
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]
где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)
Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:
[qleft( z right) = – pi {a^2}sqrt {2gz} ,]
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что
[frac{R}{H} = frac{r}{z}.]
Следовательно, площадь поверхности жидкости на высоте (z) будет равна
[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]
Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:
[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
После простых преобразований получаем следующее дифференциальное уравнение:
[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]
Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)
[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]
Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:
[T = sqrt {frac{{2H}}{g}}. ]
Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?
Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]
В данном случае площадь поперечного сечения (Sleft( z right)) является константой:
[Sleft( z right) = S = pi {R^2},]
и поток жидкости, вытекающей из сосуда, определяется формулой:
[qleft( z right) = – kz,]
где (k) зависит от размера отверстия, смачиваемости и других параметров.
В результате получаем простое дифференциальное уравнение:
[pi {R^2}frac{{dz}}{{dt}} = – kz,]
или после разделения переменных:
[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]
Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)
[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]
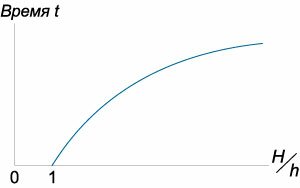
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)
Источник
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
- Участник: Котякина Анна Владиславовна
- Руководитель: Федорова Светлана Ивановна
Опыты на тему “Удивительное давление”
Опыт 1. Учебник А.В. Перышкин, Физика -7, (Задание после § 40 на стр.118 )
Цель опыта: выяснить, почему вода вытекает из отверстий и проверить гипотезу, что давление жидкости увеличивается с глубиной.
Оборудование: пластиковая бутылка, скотч, вода.
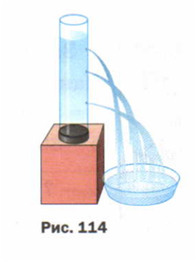
Ход эксперимента: Возьмем пластиковую бутылку. Проколем шилом или толстой нагретой иголкой три отверстия на разной высоте. Заклеим их скотчем. Нальем в бутылку воды и уберем скотч. Вода начнет вытекать из отверстий. Но что мы заметим? Чем ниже расположено отверстие, тем сильнее бьет из нее вода. По мере понижения воды в бутылке дальность вытекания воды уменьшается.
Объяснение эксперимента: Почему же так происходит? На жидкости, как и на все тела, находящиеся на Земле, действует сила тяжести. Поэтому каждый слой жидкости, налитый в сосуд, имеет свой вес. Верхние слои воды давят своим весом на расположенные ниже слои. А ниже лежащие передают давление во все стороны, в том числе и на стенки бутылки. Под действием этого давления вода выливается из бутылки с разным напором струи: чем ниже слой, тем давление жидкости будет больше.
Вывод: Опыт показывает, что внутри жидкости существует давление и на одном уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.
Применение рассматриваемого явления на практике: На глубинах более 1,5 м разность между давлением воды, сжимающим грудную клетку, и давлением воздуха внутри нее возрастает настолько, что у человека уже не хватает сил увеличивать объем грудной клетки при вдохе и наполнять свежим воздухом легкие. Поэтому при погружении более чем на 1,5 м можно дышать только таким воздухом, который сжат до давления, равного давлению воды на этой глубине. Человек при специальной тренировке может без особых предохранительных средств погружаться на глубины до 80 м, давление воды на таких глубинах около 800 кПа. На больших глубинах, если не принять специальных мер защиты, грудная клетка человека может не выдержать давления воды. На глубину до 90 м водолазы могут опускаться под воду, беря с собой запас сжатого воздуха, накачанного в прочные стальные баллоны. Такое снаряжение называют аквалангом. Аквалангом пользуются и спортсмены-пловцы.
На какую глубину может погрузиться человек?
- искатели жемчуга – 30 м.
- рекордное погружение человека без специального оснащения – 124 м. Новозеландский фридайвер Уильям Трабридж установил свой 16 мировой рекорд. Близ Багамских Островов он погрузился на глубину в 124 метра.
- погружение с аквалангом – 143 м. Опытный египетский инструктор по дайвингу и профессиональный технический дайвер Ахмед Габр установил новый мировой рекорд по наибольшей глубине погружения. 18 сентября 2014 г. ему удалось достичь отметки 332,4 метров ниже поверхности воды Красного моря неподалеку от города Дахаб. Чтобы побить предыдущий рекорд, Ахмед должен был опуститься по крайней мере на 330 метров (1083 футов) – именно таким был мировой рекорд француза Паскаля Бернабе, установленный 5 июня 2005 года в Порто-Веккьо. В конце концов, Ахмед Габр благополучно удалось достичь отметки – 332,4 метров (–1 090,5 футов).
- в мягком скафандре – 180 м
- в жестком скафандре – 250 м
- в батискафе – 10 919 м.
Интересные факты
Давление воды в глубинах океана огромно. Если пустую закупоренную бутылку опустить на значительную глубину, затем извлечь вновь, то обнаружится, что давление воды вогнало пробку внутрь бутылки, и она вся будет полна воды.
Опыт 2. Учебник А.В. Перышкин, Физика -7, (Упр. 16, задание №4 на стр. 111).
Цель опыта: экспериментально доказать справедливость закона Паскаля.
Оборудование: целлофановый пакет, вода, игла.
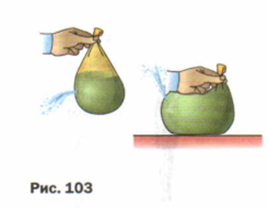
Ход эксперимента: Возьмем целлофановый пакет, проделаем несколько отверстий. Нальем воды и немного надавим. Напор вытекающих струй увеличится. Причем вода будет вытекать из всех отверстий сразу.
Объяснение эксперимента: Почему же так происходит? Все дело в строении вещества. В отличие от твердых тел отдельные молекулы жидкости могут перемещаться относительно друг друга по всем направлениям. Частицы воды, находящиеся в пакете, уплотняясь при надавливании, передают давление другим слоям жидкости, заполняющей пакет. Таким образом, давление передается в каждую точку жидкости согласно закону Паскаля, который гласит, что давление, производимое на жидкость или газ, передается в любую точку без изменения во всех направлениях.
Применение рассматриваемого явления в жизни и быту: закон Паскаля лежит в основе работы таких устройств как гидравлические прессы, гидравлические подъемники, опрыскиватели, в пневматической системе водоснабжения, водометов, а также в гидравлических тормозах автомашин. При выдавливании краски для волос при окрашивании в парикмахерских используют специальные устройства для того, чтобы выжать краску из тюбика. При надавливании рукой на тюбик краска по закону Паскаля будет передавать давление в разных направлениях, и, если не применять это устройство, то краску полностью не получиться выдавить.

1. гидравлический домкрат

2. Использование действия закона Паскаля для полива огорода
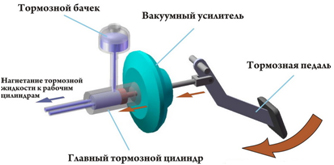
3. гидравлический тормоз

4. Приспособление для выдавливания зубной пасты
Опыт 3. Учебник А.В. Перышкин, Физика -7 (Задание №2 на стр. 125)
Цель опыта: выяснить, почему вода вытекает из отверстий только в том случае, когда крышка в бутылке открыта. В случае, когда бутылка закрыта, вода не вытекает.
Оборудование: пластиковая бутылка, вода
Ход эксперимента: Нальем воду в пластиковую бутылку. Закроем бутылку крышкой. Шилом проткнем отверстие. Что мы видим? Вода не вытекает из бутылки. Когда мы откроем крышку, вода свободно начнет выливаться из бутылки. Можно сделать вывод: вода вытекает из отверстий только в том случае, когда крышка в бутылке открыта. В случае, когда бутылка закрыта, вода не вытекать не будет.
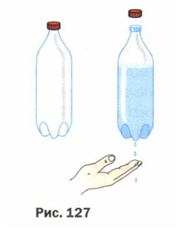
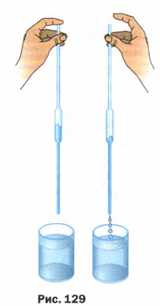
Объяснение опыта: Это происходит потому, что на нее действует только внутреннее давление в бутылке, а оно мало по сравнению с давлением атмосферы снаружи, т.е. мало для того, чтобы вытеснить воду из бутылки. Но как только мы откроем крышку, вода начнет выливаться, так как на воду еще начнет действовать атмосферное давление, а оно уже способно вытолкнуть воду из отверстия. Такое же явление можно наблюдать при работе ливера. Принцип действия, так же как и в предыдущем опыте, основан на действии атмосферного давления. Ливер опускают в воду или любую другую жидкость, Закрывают верхнее отверстие и вынимают из жидкости. Вода не вытекает из ливера. Открываем верхнее отверстие ливера и жидкость выльется. Это происходит потому, что когда мы закрываем пальцем верхнее отверстие, то на столб жидкости, который находится в ливере, действует только внутренне давление, а оно мало, и не способно вытолкнуть жидкость. Открываем верхнее отверстие ливера и жидкость выливает. Это происходит потому, что атмосферное давление сверху на жидкость и давление жидкости, вместе взятые, больше атмосферного давления снизу на жидкость.
Применение рассматриваемого явления на практике и в быту: Данное явление используется в жизни. Зная объяснение данного явления можно изготовить простейшего румойник из пластиковой бутылки. Такой рукомойник можно использовать в походных условиях или на даче. Также это явление лежит в основе работы ливера, который используют для проведения анализов различных жидкостей, в том числе и анализе качества молока.
5. Рукомойник в походных условиях

6. Анализ молока
Ссылка на видео опытов Котякиной Анны https://drive.google.com/drive/u/1/folders/0B21IX7I1ibJmVnZ4MGFKSGxaNWc
Источник
Тема. Решение задач по теме “Гидростатика и гидродинамика”.
Цели:
- – рассмотреть основные приемы решения расчетных задач на тему “Гидростатика и гидродинамика”.
Ход занятия
В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач.
Прежде чем приступить к выполнению задания, следует повторить основные законы гидромеханики.
Основной закон гидростатики – закон Паскаля, согласно которому в состоянии равновесия давление жидкости в данной точке не зависит от ориентации площадки, на которую она действует.
Поскольку в школьном курсе рассматривается стационарное течение несжимаемой жидкости, то будет справедливо уравнение неразрывности струи.
Для идеальной жидкости выполняется уравнение Бернулли. Покажите, что уравнение Бернулли является следствием закона сохранения энергии.
Качественные задачи
- К концам равноплечного рычага подвесили две одинаковые гири. Что произойдет, если одну гирю поместить в воду, а другую в керосин?
Ответ: равновесие нарушится.
- Почему, если близко стоишь около быстро идущего поезда, возникает эффект “притягивания” к колесам?
Ответ: проходящий поезд увлекает за собой примыкающие к нему слои воздуха. Воздух, движущийся между человеком и поездом, оказывает на него меньшее давление, чем неподвижный. Эта разность давлений и обусловливает силу, увлекающую человека к поезду.
- При испытании реактивного снаряда, установленного в хвосте самолета для защиты его от нападения сзади, был обнаружен удивительный факт: при пуске снаряд разворачивался и догонял свой самолет. Как можно объяснить это явление?
- Проделайте эксперимент. Вложите в воронку бумажный фильтр (рис. 1) и попробуйте выдуть его через узкий конец воронки. У вас не получилось? Почему?
Ответ: чем сильнее вы вдуваете воздух, тем плотнее фильтр входит в воронку. Объясняется это с помощью закона Бернулли, согласно которому давление понижается в местах сужения. В узком просвете между воронкой и бумажным фильтром давление понижается, и внешнее атмосферное давление удерживает фильтр в воронке.
Примеры решения расчетных задач
Задача 1. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S1, сечение струи S2 (рис. 2). Найдите ускорение, с которым перемещается уровень воды в сосуде.
Решение:
Будем считать жидкость несжимаемой. Тогда для каждого момента времени, согласно уравнению неразрывности струи, можно записать
S1v1 = S2v2, (1)
где v1 – скорость воды в сосуде, v2 – скорость воды в струе вблизи отверстия.
Возьмем производную по времени от (1)
,
где – ускорение воды в сосуде, – ускорение свободного падения, так на выходе из сосуда вода начинает свободно падать. Таким образом,
.
Ответ: .
Задача 2. В сосуде с жидкостью сделано отверстие площадью S. Размеры отверстия малы по сравнению с высотой столба жидкости. В одном случае отверстие закрыто пластинкой и измеряется сила давления жидкости на пластинку F1 при высоте столба жидкости h (рис. 3). В другом случае тот же сосуд стоит на тележке, отверстие открыто, и измеряется сила отдачи F2 при установившемся токе жидкости в момент, когда высота столба жидкости будет та же, что и в первом случае. Будут ли силы F1 и F2 равны?
Решение:
Согласно закону Паскаля давление на жидкость передается во всех направлениях одинаково, поэтому в первом случае давление, производимое на пластинку жидкостью, равно гидростатическому давлению столба жидкости высотой h, а значит, F1 = ρghS , где ρ – плотность жидкости.
Во втором случае сила F2 согласно второму закону Ньютона равна изменению импульса жидкости в единицу времени
.
Изменение импульса Δp = Δmv , где Δm – масса жидкости, вытекающей в единицу времени, v – скорость истечения жидкости из отверстия.
Масса вытекающей жидкости Δm = ρgS, скорость истечения согласно формуле Торричелли . Следовательно,
F2 = ρv2S = 2ρghS.
Таким образом, F2 = 2F1 . Объяснить это можно так. Когда жидкость вытекает из малого отверстия, линии тока вблизи него сгущаются, а значит, как следует из уравнения Бернулли, давление на стенку вблизи отверстия уменьшается. Поэтому сила реакции вытекающей струи оказывается больше силы статического давления на площадь отверстия.
Ответ: силы F1 и F2 не равны.
Задача 3. Из крана выливается вода. Начиная с некоторого места, диаметр струи уменьшается на протяжении h от а до b (рис. 3). Сколько воды вытечет из крана за время t?
Решение:
Воспользуемся условием стационарности течения несжимаемой жидкости
. (1)
Для идеальной жидкости справедливо уравнение Бернулли:
.
Поскольку жидкость свободно падает, то давления в обоих сечениях одинаковы, и уравнение Бернулли принимает вид:
. (2)
За время t через любое сечение протекает один и тот же объем воды, поэтому можно записать
. (3)
Выразим скорость v1 из (1) и (2):
.
Подставим полученное значение v1 в (3) и получим окончательный ответ:
.
Ответ: .
Задача 4. Площадь поршня в шприце S1 = 2 см2, а площадь отверстия S2 = 1 мм2 (рис. 4). Сколько времени будет вытекать вода из шприца, если действовать на поршень с силой F = 5 H и если ход поршня l = 5 см?
Решение:
Так как из шприца вытечет вся находившаяся в нем жидкость, то
S1l = S2v2t, (5)
где v2 – скорость истечения струи. Будем считать жидкость идеальной, тогда можно использовать уравнение Бернулли:
.
Шприц расположен горизонтально, следовательно, h = const. Уравнение Бернулли тогда запишется следующим образом:
, (6)
где Ра – атмосферное давление, а v1 – скорость движения поршня. Из уравнения неразрывности следует
S1v1 = S2v2. (7)
Решая совместно уравнения (6) и (7), получим
,
отсюда
.
Подставляя найденное значение v2 в (5), получим
.
Так как S2S1 , то можно записать
.
Ответ:
Задачи для самостоятельной работы
- “Вечерело. Уставший за нелегкий трудовой день Абдулла Ибн Сауд присел на берегу реки и стал обдумывать свой социальный статус. В колхоз не берут, кооперативы эмир разогнал, к нему самому на службу устраиваться – так стражники без золотых во дворец не пускают. Эх, жизнь… Но тут взгляд Абдуллы остановился: по реке плыл какой-то предмет, и лишь маленький кусочек сургуча был виден над водой. Абдулла бросился в воду и вытащил оттуда старинный глиняный кувшин, герметично закупоренный сургучом. Распечатав кувшин и перевернув его, Абдулла обомлел: сверкнуло золото. Из кувшина высыпалось 147 одинаковых золотых монет. Монеты Абдулла спрятал, а сосуд запечатал и бросил обратно в воду. Поплыл сосуд дальше, примерно треть его объема торчало над водой”.
Так говорится в одной из восточных сказок. Предполагая, что кувшин был двухлитровый, оцените массу одной золотой монеты.Ответ: m = 4,45 г.
- На некоторых железных дорогах пополнение паровозного котла водой производится без остановки паровоза. Для этой цели применяется изогнутая под прямым углом труба, которая опускается на ходу паровоза в канаву с водой, проложенную вдоль рельсов. При какой скорости паровоза вода может подняться на высоту 3 м?
Ответ: v = 28 км/ч.
- Из поднятого на высоту h резервуара выходит труба постоянного сечения S, переходящая в короткую трубу сечением S1, перекрытую краном. Найдите давление в магистральной трубе при открытом кране.
Ответ: Р = Ратм + ρgh.
- Определите расход воды Q, протекающей через слив плотины, имеющей ширину l, глубину потока d и понижение уровня потока по сравнению с уровнем воды в водохранилище, равное h.
Ответ: Q = ρdl·√(2gh).
- Какова примерно скорость катера, если при его движении вода поднимается вдоль его носовой части
на высоту h = 1 м?Ответ: v ≈ √(2gh) ≈ 4,4 м/с.
- На гладкой горизонтальной поверхности стоит цилиндрический сосуд с водой. В боковой стене сосуда у дна имеется отверстие площадью S0. Какую силу нужно приложить к сосуду в горизонтальном направлении, чтобы удержать его в равновесии? Площадь поперечного сечения сосуда равна S, высота столба жидкости h.
Ответ: .
- На поршень шприца площади S действует сила F. С какой скоростью v должна вытекать в горизонтальном направлении струя из отверстия иглы площади s? Плотность жидкости ρ. Трением пренебречь.
Ответ: . Если s S, то .
Рекомендуемая литература
- Бутиков Е.И., Кондратьев А.С. Физика. Т. 1. Механика. – М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. – С. 332-352.
- Физика. Механика / Под ред. Г.Я. Мякишева. – М.: Просвещение, 1995. – С. 420-436.
- Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. – М.: Физматлит, 2005. – С. 63-67.
- Готовцев В.В. Лучшие задачи по механике и термодинамике. – М.; Ростов н/Д: Издательский центр “Март”, 2004. – С. 184-212.
Источник