Под давлением 50 кпа и при температуре 100 в закрытом сосуде

25. Молекулярная физика (Расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В начальный момент времени газ имел давление (p=15cdot10^4) Па при (t = 100 ^{circ}C). Затем газ изотермически сжали в (k = 4) раз. В результате давление газа увеличилось в 2 раза. Определите относительную влажность в начальный момент времени. Потерями вещества пренебречь. Ответ дайте в процентах.
Давление насыщенного водяного пара при 100 (^{circ}C) равно (10^5) Па.
Так как объем умеьшился в 4 раза, а давление увеличилось только в 2 раза, то это означает, что часть пара сконденсировалось и пар стал насыщенным, то есть [p_{text{вод пар}}=p_{text{нас.пар}}=100text{ кПа}] Где (p_{text{вод.п.}}) – давление водяных паров, (p_{text{нас.п.}}) – давление насыщенных паров. Суммарное конечное давление равно [p_2=2p_1=300 text{ кПа}] Закон Дальтона (давление смеси равно сумме парциальных давлений компонентов): [p_{text{см}}=p_1+p_2+dots+p_n] [p_{text{см}}=p_{text{возд}}+p_{text{вод.пар}}] [p_{text{возд}}=p_{text{см}}-p_{text{вод.пар}}=400text{ кПа}-100text{ кПа}=300 text{кПа}] Давление воздуха подчиняется изотермическому процессу (так как масса воздуха не меняется), значит в начальный момент давление воздуха было в 4 раза меньше: [p_{0text{возд}}=frac{300cdot10^3}{4}=75 text{ кПа}] [p_{text{см}}=p_{text{возд}}+p_{text{вод.пар}}] [p_{0text{вод.пар}}=p_{0text{см}}-p_{0text{возд}}=150text{ кПа}-75text{ кПа}=75 text{ кПа}]
Влажность воздуха: [varphi=frac{p_{text{вод.пар}}}{p_{text{нас.пар}}}] [varphi=frac{75text{ кПа}}{100text{ кПа}}=0,75=75%]
Ответ: 75
В сосуде объёмом 3 л при температуре +70 (^{circ})С находится смесь воздуха с водяными парами. Давление в сосуде равно 99,2 кПа, относительная влажность воздуха 50(%). Давление насыщенного водяного пара при данной температуре равно 31,1 кПа. Какое количество воздуха находится в сосуде? Ответ выразите в миллимолях и округлите до целого числа.
Влажность воздуха: [varphi=dfrac{p_{text{вод.пар}}}{p_{text{нас.пар}}} ; ; ; Rightarrow ; ; ; p_{text{вод.пар}}=varphi cdot p_{text{нас.пар}}] где (p_{text{вод.п.}}) — давление водяных паров, (p_{text{н.п.}}) — давление насыщенных паров. [p_{text{вод.пар}}=0,5cdot31,1text{ кПа}=15,55 text{ кПа}] По закону Дальтона, давление смеси равно сумме парциальных давлений компонентов: [p_{text{см}}=p_1+p_2+dots+p_n] [p_{text{см}}=p_{text{возд}}+p_{text{вод.пар}} ; ; ; Rightarrow ; ; ; p_{text{возд}}=p_{text{см}}-p_{text{вод.пар}}] [p_{text{возд}}=99,2text{ кПа}-15,55text{ кПа}=83,65 text{кПа}] Запишем уравнение Менделеева – Клапейрона для воздуха: [p_{text{возд}}V=nu RT] где (V) — объем газа, (nu) — количество вещества, (R) — универсальная газовая постоянная, (T) — температура газа в Кельвинах.
Вырразим количесвто веещества: [nu=dfrac{p_{text{возд}}V}{RT}] [nu=dfrac{83,65cdot10^3text{ Па}cdot3cdot10^{-3}text{ м}^3}{8,31text{ Дж/(моль$cdot$К)}cdot(70+273)text{ К}} approx 88 text{ ммоль}]
Ответ: 88
В большом сосуде с жёсткими стенками, закрытом подвижным поршнем, находятся воздух и насыщенный водяной пар при температуре 100 (^{circ})С. Давление в сосуде равно 150 кПа. Поршень переместили, поддерживая температуру содержимого сосуда постоянной. При этом половина водяного пара сконденсировалась. Какое давление установилось в сосуде? Ответ выразите в кПа.
В сосуде находятся воздух и насыщенный пар, при этом давление в сосуде состоит из суммы давлений этих двух газов: [p=p_1+p_2] Так как водяной пар насыщенный, то его давление при 100 (^{circ})С равно 100 кПа: (p_1) = 100 кПа.
Тогда давление воздуха равно: [p_2=150text{ кПа}-100text{ кПа}=50text{ кПа}] Половина водяного пара сконденисровалась, это означает, что объем уменьшили в 2 раза.
Давление водяных паров не изменилось, так как пар насыщенный.
Давление воздуха увеличилось в 2 раза, потому что объем уменьшился в 2 раза, температура не меняется.
Таким образом, давление в конечном сосстоянии в сосуде: [p=p_1+p’_2] [p =100text{ кПа}+50text{ кПа}cdot2=200 text{ кПа}]
Ответ: 200
В закрытом сосуде находится 4 г водяного пара под давлением 50 кПа и при температуре 100 (^{circ})С. Не изменяя температуры, объём сосуда уменьшили в 4 раза. Найдите массу образовавшейся при этом воды. Ответ приведите в граммах.
Влажность воздуха: [varphi=dfrac{p_{text{вод.пар}}}{p_{text{нас.пар}}}] где (p_{text{вод.п.}}) — давление водяных паров, (p_{text{нас.п.}}) — давление насыщенных паров.
Давление насыщенного водяного пара при 100 (^{circ})С равно 10(^5) Па.
Так как объем умеьшился в 4 раза, а максимальное давление (10^5) Па (100 кПа), то давление может увеличиться только в 2 раза.
Запишем уравнение Менделеева – Клапейрона для водяного пара: [p_{text{вод.пар}}V=dfrac{m}{mu} RT] где (mu) — молярная масса газа, (V) — объем газа, (m) — масса пара, (R) — универсальная газовая постоянная, (T) — температура пара в Кельвинах.
Из закона видно, что для уменьшения объема в 4 раза (так как давление увеличится в 2 раза) необходимо уменьшение массы водяного пара в 2 раза (то есть половина водяного пара сконденсируется): [m_{text{вод}}=dfrac{m_{text{пар}}}{2}=2text{ г}]
Ответ: 2
В сосуде под поршнем находится 3г водяного пара под давлением 25 кПа при температуре 100 (^circ)С. Объем сосуда изотермически уменьшили в 3 раза, найдите массу образовавшейся воды. Ответ дайте в граммах.
Давление насыщенных паров при 100 (^circ)С равно 100кПа. Найдем влажность пара в сосуде по формуле: [phi=dfrac{p}{p_text{ н.п.}}100%] где (p) — давление газа, (p_text{ н.п.}) — давление насыщенных паров при данной температуре.
Так как объем сосуда изотермически уменьшили, то по закону Бойля – Мариотта: (pV=const), где (V) объем газа.
А значи, при уменьшении объема в 3 раза, давление возрастает в 3 раза.
Тогда влажность равна: [varphi=dfrac{3cdot 25text{ кПа}}{100text{ кПа}}cdot100%=75%] Так как влажность меньше 100% то водяные пары не будут конденсироваться, а значит масса водяного пара не будет увеличиваться.
Ответ: 0
Источник
Задача 28.
При 17°С некоторое количество газа занимает объем 580 мл. Какой объем займет это же количество газа при 100°С, если давление его останется неизменным?
Решение:
По закону Гей – Люссака при постоянном давлении объём газа изменяется прямо пропорционально абсолютной температуре (Т):

V2 – искомый объём газа;
T2 – соответствующая V2 температура;
V1 – начальный объём газа при соответствующей температуре Т1.
По условию задачи V1 = 580мл; Т1 = 290К (273 + 17 = 290) и Т2 = 373К (273 + 100 = 373). Подставляя эти значения в выражение закона Гей – Люссака, получим:

Ответ: V2 = 746мл.
Задача 29.
Давление газа, занимающего объем 2,5л, равно 121,6 кПа (912мм рт. ст.). Чему будет равно давление, если, не изменяя температуры, сжать газ до объема в 1л?
Решение:
Согласно закону Бойля – Мариотта, при постоянной температуре давление, производимое данной массой газа, обратно пропорционально объёму газа:

Обозначив искомое давление газа через Р2, можно записать:

Ответ: Р2 = 304кПа (2280мм.рт.ст.).
Задача 30. На сколько градусов надо нагреть газ, находящийся в закрытом сосуде при 0 °С, чтобы давление его увеличилось вдвое?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально температуре:

По условию задачи Т1 = 0 °С + 273 = 273К; давление возросло в два раза: Р2 = 2Р1.
Подставляя эти значения в уравнение, находим:

Ответ: Газ нужно нагреть на 2730С.
Задача 31.
При 27°С и давлении 720 мм.рт. ст. объем газа равен 5л. Кой объем займет это же количество газа при 39°С и давлении 104кПа?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 5л; Т = 298К (273 + 25 = 298); Р = 720 мм.рт.ст. (5,99 кПа); Р0 = 104 кПа; Т = 312К (273 + 39 = 312); Т = 273К. Подставляя данные задачи в уравнение, получим:

Ответ: V0 = 4,8л
Задача 32.
При 7°С давление газа в закрытом сосуде равно 96,0 кПа. Каким станет давление, если охладить сосуд до —33 °С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 96,0 кПа; Т1 = 280К (273 + 7 = 280); Т2 = 240К (273 – 33 = 240). Подставляя эти значения в уравнение, получим:

Ответ: Р2 = 82,3кПа.
Задача 33.
При нормальных условиях 1г воздуха занимает объем 773 мл. Какой объем займет та же масса воздуха при 0 °С и )и давлении, равном 93,3 кПа (700мм. рт. ст.)?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V0 = 773мл; Т0 = 298К (273 + 25 = 298); Т = 273К; Р = 93,3кПа. Подставляя данные задачи и преобразуя уравнение, получим:

Ответ: V = 769, 07 мл.
Задача 34.
Давление газа в закрытом сосуде при 12°С равно 100 кПа (750мм рт. ст.). Каким станет давление газа, если нагреть сосуд до 30°С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 100 кПа; Т1 = 285К (273 + 12 = 285); Т2 = 303К (273 + 30 = 303). Подставляя эти значения в уравнение, получим:

Ответ: Р2 = 106,3кПа.
Задача 35.
В стальном баллоне вместимостью 12л находится при 0°С кислород под давлением 15,2 МПа. Какой объем кислорода, находящегося при нормальных условиях можно получить из такого баллона?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 12л; Т = 273К (273 + 0 = 2273); Р =15,2МПа); Р0 = 101,325кПа; Т0 = 298К (273 + 25 = 298). Подставляя данные задачи в уравнение, получим:

Ответ: V0 = 1,97м3.
Задача 36.
Температура азота, находящегося в стальном баллоне под давлением 12,5 МПа, равна 17°С. Предельное давление для баллона 20,3МПа. При какой температуре давление азота достигнет предельного значения?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:

Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 12,5МПа; Т1 = 290К (273 + 17 = 290); Р2 = 20,3МПа. Подставляя эти значения в уравнение, получим:

Ответ: Т2 = 1980С.
Задача 37.
При давлении 98,7кПа и температуре 91°С некоторое количество газа занимает объем 680 мл. Найти объем газа при нормальных условиях.
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:

где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V = 680мл; Т0 = 298К (273 + 25 = 298); Т = 364К (273 + 91 = 364); Р = 98,7кПа. Подставляя данные задачи и преобразуя уравнение, получим:
<

Ответ: V0 = 542,3мл.
Задача 38.
При взаимодействии 1,28г металла с водой выделилось 380 мл водорода, измеренного при 21°С и давлении 104,5кПа (784мм рт. ст.). Найти эквивалентную массу металла.
Решение:
Находим объём выделившегося водорода при нормальных условиях, используя уравнение:

где Р и V – давление и объём газа при температуре Т = 294К (273 +21 = 294); Р0 = 101,325кПа; Т0 = 273К; Р = 104,5кПа. Подставляя данные задачи в уравнение,
получим:

Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):

Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 22,4 : 2 = 11,2л или 11200 мл. Тогда, используя формулу закона эквивалентов, рассчитаем эквивалентную массу металла:

Ответ: mЭ(Ме) = 39,4г/моль.
Задача 39.
Как следует изменить условия, чтобы увеличение массы данного газа не привело к возрастанию его объема: а) понизить температуру; б) увеличить давление; в) нельзя подобрать условий?
Решение:
Для характеристики газа количеством вещества (n, моль) применяется уравнение РV = nRT, или – это уравнение Клапейрона-Менделеева. Оно связывает массу (m, кг); температуру (Т, К); давление (Р, Па) и объём (V, м3) газа с молярной массой (М, кг/моль).
Тогда из уравнения Клапейрона-Менделеева объём газа можно рассчитать по выражению:

Отсюда следует, что V = const, если при увеличении массы (m) газа на некоторую величину будет соответственно уменьшена температура (T) системы на некоторое необходимое значение. Объём системы также не изменится при постоянной температуре, если при увеличении массы (m) газа на некоторую величину будет соответственно увеличено давление (P) системы на необходимую величину.
Таким образом, при увеличении массы газа объём системы не изменится, если понизить температуру системы или же увеличить давление в ней на некоторую величину.
Ответ: а); б).
Задача 40.
Какие значения температуры и давления соответствуют нормальным условиям для газов: а) t = 25 °С, Р = 760 мм. рт. ст.; б) t = 0 °С, Р = 1,013 • 105Па; в) t = 0°С, Р = 760 мм. рт. ст.?
Решение:
Состояние газа характеризуется температурой, давлением и объёмом. Если температура газа равна 0 °С (273К), а давление составляет 101325 Па (1,013 • 105) или 760 мм. рт. ст., то условия, при которых находится газ, принято считать нормальными.
Ответ: б); в).
Источник
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 64%
Ответом к заданию 10 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Сколько керосина необходимо сжечь, чтобы 50 л воды нагреть от 20◦C до кипения? КПД нагревателя равен 35%. Удельная теплота сгорания керосина 4,3 · 107 Дж/кг. Ответ выразите в (кг), округлив до десятых.
Решение
Дано:
$V=50·10^{-3}м^3$
$ρ_в=10^3{кг}/{м^3}$
$t_1=20°C; t_2=100°C; η=0.35$
$q=4.3·10^7$Дж/кг
$c=4200$Дж/кг·К
$m-?$
Решение:
$Q_1=q·m$(1) – количество теплоты, которое выделяется при сжимании керосина, $m$ – масса керосина. $Q_2=c·m_в·(t_2-t_1)=c·ρ·V·(t_2-t_1)$(2) – количество теплоты, которое необходимо затратить, чтобы нагреть воду массой $m_в=ρ·V$(3), где $ρ$ – плотность воды, $c$ – удельная теплоемкость воды.
КПД нагревателя определяется выражением: $η={A_{полез}}/{A_{затр}}·100%={c·ρ·V·(t_2-t_1)}/{q_m}·100%$(4), откуда $m={c·ρ·V·(t_2-t_1)·100%}/{q·η}$(5). Подставим в (5): $m={4200·10^3·50·10^{-3}·(100-20)·100%}/{4.3·10^7·35%}={4.2·5·8}/{4.3·35}=1.1$кг.
Ответ: 1.1
Показать решение
Полный курс
Задача 2
В подвальном помещении относительная влажность воздуха 70%, а парциальное давление водяных паров 2100 Па. Чему равно давление насыщенных паров при той же температуре? Ответ выразите в (кПа).
Решение
Дано:
$p=2100$Па
$ϕ=70%$
$p_н-?$
Решение:
Относительная влажность воздуха равна: $ϕ={p}/{p_н}·100%$, откуда давление насыщенных паров $p_н$ равно: $p_н={p·100%}/{ϕ}={2100·100%}/{70%}=3000=3$кПа.
Ответ: 3
Показать решение
Полный курс
Задача 3
Определите КПД нагревателя, расходующего 80 г керосина на нагревание 3 л воды на 90 К. Удельная теплота сгорания керосина 4,3·107 Дж/кг. Ответ выразите в (%).
Решение
Дано:
$m_к=0.08$кг
$V_в=3=3·10^{-3}м^3$
$ρ_в=1000{кг}/{м^3}$
$∆T=90K$
$q=4.3·10^7$Дж/кг
$c=4200$Дж/кг·К
$η-?$
Решение:
КПД нагревателя определяется выражением: $η={A_{полез}}/{A_{затр}}·100%$(1), $m_в=ρ_в·V_в$(2) – масса воды, где $A_{полез}=Q_п=cm_в·∆T=c·ρ_в·V_в·∆T$(3) – полезная работа; $A_{затр}=Q_з=q·m_к$(4) – затраченная (полезная) работа. Подставим (3) и (4) в (1) получим: $η={c·ρ_в·V_в·∆T}/{q·m_к}·100%={4200·10^3·3·10^{-3}·90}/{4.3·10^7·8·10^{-2}}·100%={1134000}/{3440000}·100%=32.965%=33%$.
Ответ: 33
Показать решение
Полный курс
Задача 4
Определите относительную влажность воздуха при комнатной температуре, если парциальное давление пара при этой температуре равно 1167 Па, а давление насыщенного пара равно 2333 Па. Ответ выразите в (%).
Решение
Дано:
$p=1167$Па
$p_0=2333$Па
$ϕ-?$
Решение:
Относительная влажность воздуха равна: $ϕ={p}/{p_0}·100%$, где $p$ – парциальное давление пара, $p_0$ – давление насыщенного пара. Подставим числа: $ϕ={1167}/{2333}·100%=0.5·100%=50%$.
Ответ: 50
Показать решение
Полный курс
Задача 5
Относительная влажность воздуха 65%, давление насыщенного пара в нём при некоторой температуре равно 3,4 кПа. Чему равно парциальное давление пара при этой же температуре? Ответ выразите в (кПа).
Решение
Дано:
$ϕ=65%$
$p_0=3.4·10^3$Па
$p-?$
Решение:
По определению относительная влажность воздуха равна: $ϕ={p}/{p_0}·100%$(1), где $p$ – парциальное давление пара. Из (1) найдем $p$: $p={ϕ·p_0}/{100%}$(2). Подставим числа: $p={65·3.4·10^3}/{100%}=2210=2.21$кПа.
Ответ: 2.21
Показать решение
Полный курс
Задача 6
Относительная влажность воздуха в закрытом сосуде под поршнем составляет 65%. Какой станет относительная влажность воздуха в сосуде, если объём воздуха в нём изотермически уменьшить в 2 раза за счёт движения поршня? Ответ выразить в (%).
Решение
Дано:
$T=const$
$ϕ_{от.в.}=65%$
$V_2={V_1}/{2}$
Решение:
Из теории известно, что при $T=const$ и уменьшении объема, увеличивается давление по закону Менделеева-Клайперона $PV=υRT$. Тогда как $P∼ϕ_{от.в.}$, но более чем 100% быть не может.
Ответ: 100
Показать решение
Полный курс
Задача 7
Относительная влажность воздуха при температуре 100◦С составляет 60%. Чему равно парциальное давление водяных паров, содержащихся в воздухе? Ответ выразить в (кПа).
Решение
Дано:
$T=100°C$
$ϕ_{от}=60%$
$P_{вп}-?$
Решение:
Известно, что для $T=100°C$ давление насыщенного пара $P_*=100$кПа. Тогда $ϕ={P_{вп}}/{P_*}·100⇒P_{вп}=0.6·100=60$кПа.
Ответ: 60
Показать решение
Полный курс
Задача 8
Давление насыщенного водяного пара при 24◦С равно 22,4 мм рт. ст., а при 13◦С — 11,23 мм рт. ст. Определите относительную влажность воздуха при температуре 24◦С, если точка росы равна 13◦С. Ответ выразите в процентах и округлите до целых. Ответ выразите в (%).
Решение
Дано:
$T’=24°C+273=297°C$
$P_{нп}=22.4$мм.рт.ст.
$T_p=13°C+273=286°C$
$P’_{нп}=11.23$мм.рт.ст.
$ϕ_{от}(T=24°C)$
Решение:
$V=const$ (изохорный), тогда: ${P_p^{нп}}/{T_p}={P_{нп}}/{T_1}⇒P_p^{нп}={P’_{нп}·T_p}/{T_1}⇒$ подставим в выражение. Тогда для нахождения $ϕ_{от}:ϕ_{от}={P_p^{нп}}/{P_{нп}}={P’_{нп}·T_p}/{T_1·P_{нп}}={11.23·286}/{297·22.4}=50%$
Ответ: 50
Показать решение
Полный курс
Задача 9
Определите массу воды, взятой при температуре 40◦С, которую нагревают до температуры кипения и полностью испаряют. Необходимая для этих процессов энергия составляет 638 кДж. Ответ выразите в (г).
Решение
Дано:
$m-?$
$T_1=40°$
$Q_{об}=638$кДж
Решение:
$c_вm∆T+r·m=Q_{об}$ – закон теплообмена.
$m={Q_{об}}/{c_в∆T+r}={6.38·10^3}/{4200·60+2.3·10^6}=250$г.
Ответ: 250
Показать решение
Полный курс
Задача 10
Какое количество теплоты необходимо для нагревания железного бруска массой 200 г от 285 К до 305 К? Ответ выразите в (Дж). Удельная теплоемкость железа 460 Дж/(кг*К)
Решение
Дано:
$m_ж=0.2кг$
$∆T=20K$
$c_ж=460$ Дж/(кг*К)/
$Q-?$
Решение:
По закону нагревания тела равно $Q=c_ж·m_x·∆T=0.460·10^3·0.2·20=1840$Дж.
Ответ: 1840
Показать решение
Полный курс
Задача 11
Каково давление насыщенного водяного пара при температуре 100◦С? Ответ выразите в (кПа).
Решение
Дано:
$p_{нв}-?$
$T=100°C$
Решение:
По определению давления насыщенного пара при $T=100°C$. Составляет 100кПа.
Ответ: 100
Показать решение
Полный курс
Задача 12
В сосуде с подвижным поршнем находятся вода и её насыщенный пар. Если одновременно увеличить в 2 раза температуру сосуда и его объём, то как увеличится его давление? В ответ запишите: примерно в _ раз(а).
Решение
1) Температура сосуда не влияет на давление, тогда по Менделееву-Клайперону $pV=υRT$. Очевидно, что давление увеличится в 2 раза.
Ответ: 2
Показать решение
Полный курс
Задача 13
Относительная влажность воздуха в цилиндре под поршнем равна 40%. Воздух изотермически сжали, уменьшив его объём в три раза. Какова стала относительная влажность воздуха? Ответ выразите в (%).
Решение
Дано:
$ϕ_{отн}=40%$
$T=const$
$V_2
$V_2={V_1}/{3}$
$ϕ_{отн}-?$
Решение:
Насыщенный пар подчиняется уравнению Менделеева-Клайперона: $ϕ={n}/{n_{нп}}·100%; n_{нп}$ – не изменяется ($T=const$)
$n=0.4n_{нп}$, следовательно, уменьшение в 3 раза приведет к увеличению $n=1.2=n_{нп}$, но $n=n_{нп}$ это максимум (насыщенный пар).
Ответ: 100
Показать решение
Полный курс
Задача 14
Относительная влажность водяного пара в сосуде при температуре 100◦С равна 62%. Какова плотность этого пара? Ответ округлите до сотых. Ответ выразить в (кг/м3).
Решение
Дано:
$ϕ_{отн}=62%$
$T=100°C$
$ρ_{вп}-?$
Решение:
Относительная влажность это отношение парциального давления паров воды в газе к равновесному давлению паров при данной температуре $ϕ={ρ}/{ρ_{вп}}$. При 100°C давление насыщенных паров равно атмосферному $ρ_{нп}=10^5$Па, тогда $ρ={ρ·M}/{R·T}={ϕ·ρ_{нп}·M}/{R·T}={0.62·10^5·0.018}/{8.31·373}=0.36{кг}/{м^3}$.
Ответ: 0.36
Показать решение
Полный курс
Задача 15
В кубическом метре воздуха в помещении при температуре 20◦С находится 1,12 · 10−2 кг водяных паров. Пользуясь таблицей плотности насыщенных паров воды, определите относительную влажность воздуха. Ответ округлите до целого. Ответ выразите в (%).
| t, ◦ C | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| ρ, г/м3 | 13,6 | 14,5 | 15,4 | 16,3 | 17,3 | 18,3 | 19,4 | 20,6 | 21,8 |
Решение
Дано:
$V=1м^3$
$T=20°C$
$m_{вп}=1.12·10^{-2}$кг
$ϕ_{отн}-?$
Решение:
1) Определим плотность водяных паров в комнате $ρ_{вп}={m_{вп}}/{V}={1.12·10^{-2}}/{1}{кг}/{м^3}$.
2) Используя таблицу, определим, и по при температуре 20°C плотность насыщенных паров равна $ρ_{нп}=1.73·10^{-2}{кг}/{м^3}$.
3) Тогда относительная влажность воздуха в комнате равна $ϕ_{отн}={ρ_{вп}}/{ρ_{нп}}={1.12·10^{-2}}/{1.73·10^{-2}}=100≈65%$.
Ответ: 65
Показать решение
Полный курс
Задача 16
Парциальное давление водяного пара в 1,25 раза меньше, чем давление насыщенного пара при той же температуре. Чему равна относительная влажность воздуха? Ответ выразите в (%).
Решение
Дано:
$p_п=p$
$p_н=1.25p$
$ϕ-?$
Решение:
Относительная влажность воздуха определяется как: $ϕ={p_п}/{p_н}·100%$, где $p_п$ – парциальное давление газа; $p_н$ – давление насыщенного газа при той же температуре, тогда имеем: $ϕ={p_п}/{p_н}·100%={p·100%}/{1.25p}=80%$
Ответ: 80
Показать решение
Полный курс
Задача 17
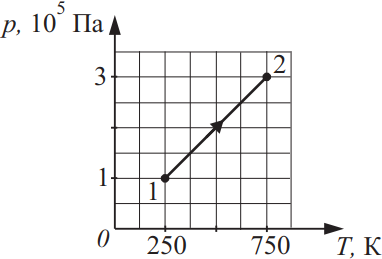
Какое количество теплоты получает 4 моля одноатомного идеального газа в процессе, график которого изображён на рисунке? Ответ выразите в (кДж).
Решение
Дано:
$υ=4$моль
$i=3$
$p_1=10^5$Па
$p_2=3·10^5$Па
$T_1=250K$
$T_2=750K$
$R=8.31{Дж}/{моль·К}$
$Q_{12}-?$
Решение:
Запишем I начало термодинамики: $Q_{12}=A_{12}+∆U_{12}$(1), где $A_{12}=p·∆V$, т.к. $V=const$ (процесс изохорный, то $∆V=0$ и работа газа $A_{12}=0$Дж).
$∆U_{12}={i}/{2}·υ·R∆T={i}/{2}υR(T_2-T_1)$(2) – изменение внутренней энергии газа, где $R$ – универсальная газовая постоянная.
Подставим (2) в (1) и найдем $Q_{12}: Q_{12}={i}/{2}υR(T_2-T_1)$(3)
Подставим числовые значения в (3): $Q_{12}={3}/{2}·4·8.31·(750-250)=24930Дж=24.93кДж$
Ответ: 24.93
Показать решение
Полный курс
Источник
