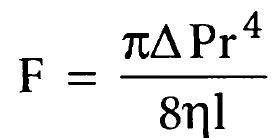Последовательное и параллельное соединение сосудов

16.
АД, его
характеристики.
При
сокращении сердца давление крови в
аорте испытывает колебания. Среднее
артериальное давление
определяется по формуле:
 ,
,
где
 – систолическое давление,
– систолическое давление, – диастолическое давление.
– диастолическое давление.
Пульс.
давл. –
разница между сист. и диаст. (30-50мм.рт.ст).
Факторы,
влияющ. на АД:
1.Объёмный
кровоток Q
= V
/ t.
2.Гидравлическое
сопротив. сосудов(чем выше тем выше АД.
17. Пульсовая
волна–
процесс распространения изменения
объема крови вдоль эластичного сосуда
в результате одновременного изменения
в нем давления и массы жидкости.
Характеристики
пульсовой волны.
Амплитудой
пульсовой волны
 (пульсовое давление)
(пульсовое давление)
называется разность между максимальным
и минимальным значением давлений в
данной точке сосуда. В начале аорты
амплитуда волны ( )
)
– максимальна и равна разности
систолического и диастолического
давлений. Затухание амплитуды пульсовой
волны при ее распространении вдоль
сосуда представлена
формулой:
 ,
,
где
 – коэффициент затухания, увеличивающийся
– коэффициент затухания, увеличивающийся
с уменьшением радиуса.
Скорость
распространения пульсовой волны
зависит от свойств сосуда и крови.
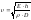 ,
,
где
 – модуль упругости;
– модуль упругости; – толщина стенки сосуда;
– толщина стенки сосуда;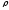 – плотность крови;
– плотность крови; – диаметрсосуда.
– диаметрсосуда.
 ,
,
что в 20-30 раз больше скорости движения
крови
 .
.
18.Рассчитаем работу,
совершаемую при однократном сокращении
сердца.
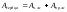 ,
,

Работа
сердца идет на продавливание (продвижение)
объема крови по аорте сечением S
на расстояние
 при среднем давленииP
при среднем давленииP
и на сообщение крови кинетической
энергии:
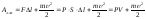 ,
,
где
 –объем крови,
–объем крови,
 – масса крови,
– масса крови,
 –плотность крови,
–плотность крови,
 – скорость течения крови.
– скорость течения крови.
 .
.
Работа
сердца при однократном сокращении равна
1 Дж.
Мощность
сердца за время систолы:
 .
.
19. Определение скорости кровотока.



20. Силовые характер. Электр. Поля
1.Напряженность
(Е):
 ,
,
 ,
,
где – пробный заряд (точечный единичный
– пробный заряд (точечный единичный
позитивный заряд, внесенный в электрическое
поле);F
– сила, действующая на заряд со стороны
электрического поля.
2.Силовые
линии
(или линии напряженности)
— это воображаемые направленные линии
в пространстве, это незамкнутые линии,
которые начинаются на положительных и
оканчиваются на отрицательных зарядах.
3.Напряженность
поля точечного заряда
определяется по формуле:
 ,
,
где q0
– заряд,
который создает электрическое поле;
r
– расстояние от точечного заряда q0
до точки,
в которой исследуется напряженность
поля;
 –коэф.
–коэф.
пропорциональности;
ε
– относительная диэлектрическая
проницаемость среды;
ε0
=
8,85 .
10 –
12
Ф/м –
электрическая постоянная.
22.Проводники– это
вещества, которые имеют свободные
заряды, способные перемещаться под
действием эл. поля.
Примеры:
плазма крови, лимфа, межклеточная
жидкость, спинномозговая жидкость,
цитоплазма.
Диэлектрики
(изоляторы)
– это вещества, которые не имеют свободных
зарядов, поэтому не проводят электрический
ток. Примеры:
сухая кожа, связки, сухожилия, костная
ткань, клеточная мембрана.
Измерение
электропроводимости (кондуктометрия)
использ.:
–
при изучении процессов в клетках и
тканях во время изменений физиологического
состояния;
–
при исследовании патологических
процессов (например, при воспалении
увеличивается электрическое сопротивление);
–
для нахождения активных точек
рефлексотерапии;
21. Энергетич.
характер. эл. поля:
1.Потенциал
( ),
),
разность потенциалов ( ).
).
 , [
, [ ]
]
=
= B.
Потенциал
– это
физическая величина численно равная
работе, которую совершают силы
электрического поля при перемещении
единичного положительного заряда из
данной точки поля в бесконечность (в
точку, где потенциал поля принимается
равным нулю).
 .
.
2.
Разность потенциалов– это
физическая величина численно равная
работе, которую совершают силы
электрического поля при перемещении
единичного положительного заряда из
точки поля 1 в 2.
 ,
,
[Δ ]
]
=B.
Paзность
потенциалов называется напряжением:
 .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
07.06.201546.36 Mб22Частная хирургия. Том1. Шевченко Ю.Л.2000г.pdf
Источник
Закон Пуазейля. Диаметр артериол и их сопротивлениеПричину такого значительного возрастания объемного кровотока при увеличении диаметра сосуда можно объяснить с помощью схемы, представленной на рисунке. На схеме показано поперечное сечение крупного и мелкого кровеносных сосудов. Концентрические слои внутри сосудов указывают на то, что скорость движения каждого слоя отличается от скорости соседних слоев, т.к. происходит ламинарное течение крови (см. ранее в данной главе). Дело в том, что слой крови, прилежащий к стенке сосуда, едва движется благодаря взаимодействию крови и эндотелия сосудистой стенки. Следующий слой крови скользит относительно пристеночного слоя и поэтому движется быстрее. Третий, четвертый, пятый и шестой слои также текут с нарастающей скоростью. Таким образом, пристеночный слой крови движется чрезвычайно медленно, в то время как по продольной оси сосуда кровь движется с наибольшей скоростью. В мелких сосудах практически вся кровь оказывается вблизи сосудистой стенки, поэтому быстротекущего центрального потока крови просто не существует. Сложив скорости всех концентрических слоев текущей крови, умноженные на площади поперечного сечения каждого слоя, можно вывести формулу, известную как закон Пуазейля:
где F — скорость кровотока, АР — разница давления на концах сосуда, r — радиус сосуда, 1 — длина сосуда и n — вязкость крови. Обратите внимание, что в этом уравнении скорость кровотока прямо пропорциональна четвертой степени радиуса сосуда. Это еще раз показывает, что среди всех факторов, определяющих скорость кровотока, диаметр кровеносного сосуда, равный двум радиусам, имеет первостепенное значение. Влияние диаметра артериол на их сопротивление (закон четвертой степени). В большом круге кровообращения почти 2/3 общего периферического сопротивления приходится на мелкие артериолы. Внутренний диаметр артериол имеет величину от 4 до 25 мкм. Однако мощная мышечная стенка артериол позволяет существенно менять внутренний диаметр, часто более чем в 4 раза. Исходя из закона четвертой степени, который определяет зависимость объемного кровотока от диаметра сосудов, четырехкратное увеличение диаметра приводит к возрастанию объемного кровотока, по меньшей мере, в 256 раз. Таким образом, незначительные изменения диаметра артериол в ответ на нервные сигналы или действие местных гуморальных факторов может привести или к почти полному прекращению кровотока в тканях, или — в других экстремальных ситуациях — резко увеличить кровоток. И действительно, в отдельных сосудистых областях регистрируется увеличение местного кровотока в 100 раз при переходе артериол из состояния максимального сужения к состоянию их максимального расширения. Сопротивление сосудов, соединенных между собой последовательно и параллельно. Кровь, которая поступает в большой круг кровообращения из сердца, движется из области с высоким давлением (аорта) в область с низким давлением крови (полые вены). Кровь течет через обширную сосудистую сеть, в которой многочисленные сосуды соединены между собой последовательно и параллельно. Артерии, артериолы, капилляры, венулы и вены в целом являются системой последовательно соединенных сосудов. Общее сопротивление такой системы представляет собой сумму сопротивлений каждого отдельного сосуда:
Следовательно, общее периферическое сопротивление равно сумме сопротивлений артерий, артериол, капилляров, венул и вен. На примере, приведенном на рисунке, общее сосудистое сопротивление равно сумме сопротивлений R1 и R2. Благодаря разветвлению сосудов формируются параллельные сосудистые сети, снабжающие кровью многочисленные органы и ткани организма. Формирование параллельных сосудистых сетей позволяет каждому органу и даже участку органа в большой степени регулировать собственный местный кровоток независимо от других органов и тканей. Очевидно, что при одном и том же градиенте давления гораздо больший объем крови будет протекать через систему параллельных сосудов, чем через любой отдельно взятый сосуд. Таким образом, общее сопротивление системы параллельных сосудов оказывается гораздо меньше, чем сопротивление любого отдельного сосуда. Кровоток через каждый из параллельных сосудов на рисунке зависит от градиента давления и сопротивления данного сосуда, а не сопротивления всей системы. Однако увеличение сопротивления одного из сосудов параллельной системы приведет к увеличению сопротивления всей системы. Кажется парадоксальным, что дополнительное увеличение количества сосудов в параллельной системе приводит к уменьшению общего сосудистого сопротивления. Дело в том, что множество параллельных сосудов облегчает протекание крови через сосудистую сеть, т.к. каждый параллельный сосуд обеспечивает дополнительный путь кровотоку, увеличивая так называемую проводимость системы для крови. Итак, общая проводимость системы параллельных сосудов (Собщая) представляет собой сумму проводимостей каждого отдельного сосуда: Собщее = С1+С2+С3+С4…. Например, сосуды головного мозга, почек, мышц, желудочно-кишечного тракта, кожи, сердца представляют собой отдельные, параллельно соединенные системы, каждая из которых вносит свой вклад в общую проводимость большого круга кровообращения. Объемный кровоток каждого органа является частью общего кровотока (сердечного выброса) и зависит от сопротивления кровотоку (или проводимости) органа так же, как и от градиента давления. Следовательно, ампутация конечности или хирургическое удаление почки приводит к удалению одной из параллельных сосудистых систем большого круга кровообращения и уменьшает общую сосудистую проводимость и объемный кровоток (т.е. сердечный выброс), в то время как общее периферическое сопротивление увеличивается. – Вернуться в оглавление раздела “Физиология человека.” Оглавление темы “Сосудистая система”: |
Источник
Любой участок сосуда (рис. 2.9) можно рассматривать как цилиндрическую трубку длины L радиуса r, по которой течет кровь.
Формулы (5), которые описывают течение Пуазейля, позволяют заключить, что величина кровотока Q, т.е. объема крови (в мл), протекающего через сосуд в единицу времени (1 сек.), пропорциональна разности давлений на входе и выходе трубы P, четвертой степени радиуса и обратно пропорциональна длине трубы

Рисунок 2.9. Течение крови по отрезку сосуда

Q= , (2.9)
где Q = кровоток (мл/мин), P = градиент давления, т.е. разность давлений на входе и выходе (в физиологии давление чаще всего измеряется в миллиметрах ртутного столба – 1 мм рт.ст.= 133 Па, 1 Па = 1 Н/м 2 – единица давления в системе СИ (м·кг·сек) ), L длина трубки (см), r внутренний радиус трубки (см), µ вязкость крови, которая в “физиологической”системе единиц (размеры – в см, давление – в мм.рт. ст., время – в минутах) равна 24 физиол.ед., тогда как в “стандартной”системе СИ µ = 5 · 103 кг/м· сек, а в “физической”системе СГС µ = 0.05 пуаза.
Это уравнение применимо только к ламинарным (без завихрений) течениям жидкости по трубке с жесткими неупругими стенками. В частности, в турбулентном режиме разность давлений пропорциональна не кровотоку, а его квадрату и может значительно превышать значения, рассчитанные по формулам ламинарного течения.
Из уравнения (9) видно, что увеличение кровотока может быть достигнуто как повышением градиента давления, так и увеличением внутреннего радиуса трубки. Оба этих механизма регулирования кровотока имеют большое значение в физиологии.
Вводя так называемое гидравлическое сопротивление, в простом случае течения Пуазейля определяющееся формулой
R: = , (2.10)
мы приходим к соотношениям между градиентом давления и кровотоком в сосуде, полностью аналогичным закону Ома для электрического тока
Q= ,или, другими словами, =·(2.11)
где кровоток Q соответствует силе электрического тока I, проходящего по проводнику, а ?P – падению напряжения U на сопротивлении R.
Формулы для электрического и гидравлического сопротивлений также аналогичны, но электрическое сопротивление обратно пропорционально квадрату, а гидравлическое – четвертой степени радиуса трубки.
Заменяя вязкость в (10) ее значением, запишем соотношения (11) между кровотоком и падением давления в отрезке сосуда в следующем виде:

Q =л, т.е. =л-1 Q; (2.12)
л = ? 60 физиол. ед., л-1 ? 0,0166 физиол. ед.
В конкретном примере, когда длина сосуда L =1 см, внутренний радиус r = 1 мм = 0.1 см, по формуле (11) находим, что для поддержания в сосуде кровотока Q =60 мл/мин разность давлений на входе и выходе сосуда должна составлять 1 мм рт. ст.
Основное уравнение гидравлики (11) применимо не только к одиночному сосуду, но и к стационарным течениям в разветвляющейся сети трубок и даже во всей системе кровообращения в целом. При этом оказывается, что эквивалентное гидравлическое сопротивление R* сосудов большого круга составляет около
R* ? 60 физиол. ед. = 133·106 кг/м2·сек. = 133·105г/см2·сек. (2.13)
Гидравлические сопротивления складываются, подобно соединению резисторов в электрических схемах (рис. 2.10), при последовательном соединении; при параллельном же соединении складываются проводимости, т.е. величина, обратная к общему сопротивлению параллельно соединенных трубок равна сумме обратных величин к сопротивлениям отдельных трубок

Рисунок 2.10. Последовательное и параллельное соединение сосудов (гидравлических проводников)

Rпосл= R1 + R2+ …Rп ; (2.14)
В общем случае, сложная сеть артериальных сосудов может являться графом, ребра которого представляют отдельные сосуды, а вершины – узлы, в которых сосуды расщепляются (или сливаются). Сопротивление каждого ребра рассчитывается по формулам (10) или (12).
Выбирая в качестве искомых неизвестных давления Pk в N ? 109 вершинах, через них по уравнению (11) записываем кровотоки во всех сосудах, удовлетворяющие (в стационарном случае) условию баланса: в каждом узле алгебраическая сумма кровотоков равна нулю.
Добавляя сюда те или иные граничные условия (например, задавая величину давления или кровотока в аорте, и приравнивая нулю давление на концах артериол), приходим к системе линейных алгебраических уравнений (СЛАУ). Практическое решение, даже на самом мощном компьютере, получающейся NхNСЛАУ не представляется возможным без дополнительных предположений, например, агрегирования (укрупнения) групп сосудов одного поколения.
На рис. 2.11 лишь левый сердечный насос и главные артерии большого круга кровообращения и последовательно с ними соединенные системы артериол (более узкие прямоугольники). Короткие черточки (как в электрических схемах) указывают на переход к капиллярной и венозной системам, давление в которых очень мало и его можно считать нулевым. Пунктиром помечены части тела, относящиеся к соответствующим участкам АСС.
Через R1, R2, R9, R10, R11 обозначены отрезки восходящей аорты, R3 – R6- коронарные артерии и артериолы, R7, R8 нисходящие ветви аорты R12 – R16 – артерии и артериолы, питающие мозг, R17- R20 – лучевые сосуды рук, R21- R24 сосуды внутренних органов, R25- R28- артериальные сосуды ног.
В табл. 2.1. приведены данные к рис. 2.11, которые будут использоваться в расчетной задаче № 3.
Таблица 2.1. Ориентировочные значения гидравлических сопротивлений (в физиологических единицах)
R1 | 2 | R8 | 20 | R15 | 200 | R22 | 150 |
R2 | 3 | R9 | 3 | R16 | 600 | R23 | 30 |
R3 | 400 | R10 | 2 | R17 | 300 | R24 | 250 |
R4 | 3600 | R11 | 2 | R18 | 1500 | R25 | 100 |
R5 | 400 | R12 | 100 | R19 | 300 | R26 | 700 |
R6 | 3600 | R13 | 100 | R20 | 1500 | R27 | 100 |
R7 | 20 | R14 | 600 | R21 | 20 | R28 | 700 |

Рис. 2.11. Схема укрупненного графа артериальной сосудистой системы человека
Важно учесть также гравитационные силы (отсутствующие лишь в состоянии невесомости), что осуществляется добавлением к давлению Pk в каждой вершине слагаемого phk, где hk высота данной точки над некоторым уровнем (обычно уровнем расположения сердца).
Несмотря на упрощенный характер гидравлического описания, оно дает возможность строить удовлетворительные модели начального приближения.
Источник
Гемодинамика (от гемо… и динамика), движение крови по сосудам, возникающее вследствие разности гидростатического давления в различных участках сосудистой системы. Разность давлений обеспечивается нагнетательной функцией сердца, выбрасывающего в сосудистую систему при каждом сокращении у человека 60—70 мл крови, что составляет в состоянии покоя 4,5—5 л/мин. Эта величина — минутный объём сердца, или сердечный выброс, — важнейший показатель функции сердечно-сосудистой системы; во время мышечной работы она может достигать 20—25 л/мин.
Кровь выбрасывается в замкнутую сосудистую систему, оказывающую сопротивление движению крови вследствие трения крови о сосудистую стенку и вязкости самой крови. При детальном математическом моделировании движения крови она рассматривается как взвесь форменных элементов, т. е. неньютоновская жидкость, а кровеносные сосуды — как вязко-эластичные трубки, свойства которых (геометрические — размеры, ветвления, и физические — вязкость, упругость, проницаемость) меняются по длине. В первом приближении трение крови о стенку сосуда зависит от размера сосуда, т. е. от его диаметра и длины. Сопротивление сосуда движению крови может быть выражено Пуазёйля законом.
Сосудистая система — серия трубок различной длины и диаметра, соединённых как последовательно, так и параллельно. При последовательном соединении (рис. 1, а) величина суммарного сопротивления равна сумме сопротивлений отдельных сосудов:
SR = R1 + R2.
При параллельном соединении (рис. 1, б)суммарное сопротивление выражается уравнением:
Наибольшим сопротивлением обладают концевые участки артерий — артериолы. Это создаёт препятствие для оттока крови из артериальной системы и приводит к созданию т. н. артериального давления (см. Кровяное давление). Его уровень (Р) пропорционален величине сосудистого сопротивления (R) и количеству крови, выбрасываемому сердцем в сосудистую систему в единицу времени (Q), т. е. P = Q·R, отсюда
Эта формула применима для всей сердечно-сосудистой системы в целом в случае, если давление в начале этой системы (т. е. в артериях) равно Р, а в конце системы (т. е. в устье полых вен) равно нулю. Если последнее не равно нулю, то уравнение приобретает несколько иной вид:
(где P1 и P2 — давление соответственно в начале и в конце сосудистой системы). Это основное уравнение Г., пользуясь которым можно определить сосудистое, или т. н. периферическое, сопротивление, если известны давления P1иP2 и минутный объём сердца (Q).
Величина периферического сопротивления в основном определяется тонусом артериол, т. е. степенью постоянного сокращения гладкой мускулатуры стенок этих сосудов. Изменение тонуса артериол регулирует уровень артериального давления в организме. Оно вызывает изменение просвета артериол и сопротивления сосудов и т. о. регулирует величину кровотока через отдельные сосудистые области, приводя его в соответствие с интенсивностью жизнедеятельности ткани, т. е. с её потребностью в кислороде и питательных веществах (в интенсивно работающих тканях, например в сокращающейся мышце, кровоток может увеличиваться в 100 и более раз, причём величина общего артериального давления и минутный объём сердца могут существенно не изменяться).
Количество крови, протекающее через все участки сосудистой системы в единицу времени, одинаково. Линейная скорость движения крови обратно пропорциональна величине суммарного просвета данного отдела сосудистого русла. Средняя линейная скорость кровотока в аорте человека достигает 50 см/сек, в капиллярах она равна 0,5 мм/сек, а в полых венах — 20 см/сек. Кровоток в аорте и крупных артериях прерывистый (пульсирующий), увеличивается при систоле (сокращении) сердца и падает почти до нуля во время диастолы (расслабления) сердца.
Взаимоотношения между суммарным просветом различных участков сосудистого русла, уровнем кровяного давления в них и скоростью кровотока представлены на рис. 2. Благодаря упругости артериальных стенок артериолы при систоле растягиваются, вмещая дополнительное количество крови, а при диастоле спадаются, способствуя проталкиванию крови в капилляры. Это обеспечивает непрерывный ток крови в капиллярах, что важно для обмена веществ между кровью и тканями.
Лит.: Чижевский A. Л, Структурный анализ движущейся крови, М., 1959; Савицкий Н. Н., Биофизические основы кровообращения и клинические методы изучения гемодинамики, 2 изд., Л., 1963; Физиология человека, М., 1966; Гайтон А., Физиология кровообращения. Минутный объем сердца и его регуляция, [пер. с англ.], М., 1969; Handbook of physiology, v. 1—3, Wash., 1962—65.
Г. И. Косицкий.

Рис. 2. Изменение скорости кровотока (1) просвета сосудов (2) и кровяного давления (3) в разных отделах сосудистого русла.

Рис. 1. Схема последовательного (а) и параллельного (б) соединения кровеносных сосудов.
Оглавление
Источник