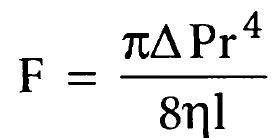Последовательное соединение сосудов это

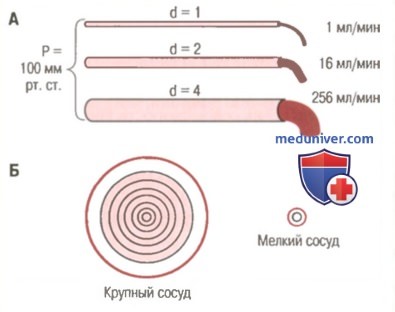
Закон Пуазейля. Диаметр артериол и их сопротивлениеПричину такого значительного возрастания объемного кровотока при увеличении диаметра сосуда можно объяснить с помощью схемы, представленной на рисунке. На схеме показано поперечное сечение крупного и мелкого кровеносных сосудов. Концентрические слои внутри сосудов указывают на то, что скорость движения каждого слоя отличается от скорости соседних слоев, т.к. происходит ламинарное течение крови (см. ранее в статьях на сайте). Дело в том, что слой крови, прилежащий к стенке сосуда, едва движется благодаря взаимодействию крови и эндотелия сосудистой стенки. Следующий слой крови скользит относительно пристеночного слоя и поэтому движется быстрее. Третий, четвертый, пятый и шестой слои также текут с нарастающей скоростью. Таким образом, пристеночный слой крови движется чрезвычайно медленно, в то время как по продольной оси сосуда кровь движется с наибольшей скоростью.
В мелких сосудах практически вся кровь оказывается вблизи сосудистой стенки, поэтому быстротекущего центрального потока крови просто не существует. Сложив скорости всех концентрических слоев текущей крови, умноженные на площади поперечного сечения каждого слоя, можно вывести формулу, известную как закон Пуазейля:
где F — скорость кровотока, ΔР — разница давления на концах сосуда, r — радиус сосуда, 1 — длина сосуда и n — вязкость крови. Обратите внимание, что в этом уравнении скорость кровотока прямо пропорциональна четвертой степени радиуса сосуда. Это еще раз показывает, что среди всех факторов, определяющих скорость кровотока, диаметр кровеносного сосуда, равный двум радиусам, имеет первостепенное значение. Влияние диаметра артериол на их сопротивление (закон четвертой степени). В большом круге кровообращения почти 2/3 общего периферического сопротивления приходится на мелкие артериолы. Внутренний диаметр артериол имеет величину от 4 до 25 мкм. Однако мощная мышечная стенка артериол позволяет существенно менять внутренний диаметр, часто более чем в 4 раза. Исходя из закона четвертой степени, который определяет зависимость объемного кровотока от диаметра сосудов, четырехкратное увеличение диаметра приводит к возрастанию объемного кровотока, по меньшей мере, в 256 раз. Таким образом, незначительные изменения диаметра артериол в ответ на нервные сигналы или действие местных гуморальных факторов может привести или к почти полному прекращению кровотока в тканях, или — в других экстремальных ситуациях — резко увеличить кровоток. И действительно, в отдельных сосудистых областях регистрируется увеличение местного кровотока в 100 раз при переходе артериол из состояния максимального сужения к состоянию их максимального расширения. Сопротивление сосудов, соединенных между собой последовательно и параллельно. Кровь, которая поступает в большой круг кровообращения из сердца, движется из области с высоким давлением (аорта) в область с низким давлением крови (полые вены). Кровь течет через обширную сосудистую сеть, в которой многочисленные сосуды соединены между собой последовательно и параллельно. Артерии, артериолы, капилляры, венулы и вены в целом являются системой последовательно соединенных сосудов. Общее сопротивление такой системы представляет собой сумму сопротивлений каждого отдельного сосуда:
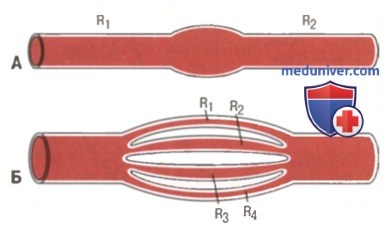
Следовательно, общее периферическое сопротивление равно сумме сопротивлений артерий, артериол, капилляров, венул и вен. На примере, приведенном на рисунке, общее сосудистое сопротивление равно сумме сопротивлений R1 и R2. Благодаря разветвлению сосудов формируются параллельные сосудистые сети, снабжающие кровью многочисленные органы и ткани организма. Формирование параллельных сосудистых сетей позволяет каждому органу и даже участку органа в большой степени регулировать собственный местный кровоток независимо от других органов и тканей. Для параллельно соединенных сосудов общее сопротивление рассчитывается следующим образом: Очевидно, что при одном и том же градиенте давления гораздо больший объем крови будет протекать через систему параллельных сосудов, чем через любой отдельно взятый сосуд. Таким образом, общее сопротивление системы параллельных сосудов оказывается гораздо меньше, чем сопротивление любого отдельного сосуда. Кровоток через каждый из параллельных сосудов на рисунке зависит от градиента давления и сопротивления данного сосуда, а не сопротивления всей системы. Однако увеличение сопротивления одного из сосудов параллельной системы приведет к увеличению сопротивления всей системы. Кажется парадоксальным, что дополнительное увеличение количества сосудов в параллельной системе приводит к уменьшению общего сосудистого сопротивления. Дело в том, что множество параллельных сосудов облегчает протекание крови через сосудистую сеть, т.к. каждый параллельный сосуд обеспечивает дополнительный путь кровотоку, увеличивая так называемую проводимость системы для крови. Итак, общая проводимость системы параллельных сосудов (Собщая) представляет собой сумму проводимостей каждого отдельного сосуда: Собщее = С1+С2+С3+С4…. Например, сосуды головного мозга, почек, мышц, желудочно-кишечного тракта, кожи, сердца представляют собой отдельные, параллельно соединенные системы, каждая из которых вносит свой вклад в общую проводимость большого круга кровообращения. Объемный кровоток каждого органа является частью общего кровотока (сердечного выброса) и зависит от сопротивления кровотоку (или проводимости) органа так же, как и от градиента давления. Следовательно, ампутация конечности или хирургическое удаление почки приводит к удалению одной из параллельных сосудистых систем большого круга кровообращения и уменьшает общую сосудистую проводимость и объемный кровоток (т.е. сердечный выброс), в то время как общее периферическое сопротивление увеличивается. – Также рекомендуем “Гематокрит. Зависимость кровотока от давления” – Вернуться в оглавление раздела “Физиология человека.” Оглавление темы “Сосудистая система”: |
Источник
Любой участок сосуда (рис. 2.9) можно рассматривать как цилиндрическую трубку длины L радиуса r, по которой течет кровь.
Формулы (5), которые описывают течение Пуазейля, позволяют заключить, что величина кровотока Q, т.е. объема крови (в мл), протекающего через сосуд в единицу времени (1 сек.), пропорциональна разности давлений на входе и выходе трубы P, четвертой степени радиуса и обратно пропорциональна длине трубы
Рисунок 2.9. Течение крови по отрезку сосуда
Q= , (2.9)
где Q = кровоток (мл/мин), P = градиент давления, т.е. разность давлений на входе и выходе (в физиологии давление чаще всего измеряется в миллиметрах ртутного столба – 1 мм рт.ст.= 133 Па, 1 Па = 1 Н/м 2 – единица давления в системе СИ (м·кг·сек) ), L длина трубки (см), r внутренний радиус трубки (см), µ вязкость крови, которая в “физиологической”системе единиц (размеры – в см, давление – в мм.рт. ст., время – в минутах) равна 24 физиол.ед., тогда как в “стандартной”системе СИ µ = 5 · 103 кг/м· сек, а в “физической”системе СГС µ = 0.05 пуаза.
Это уравнение применимо только к ламинарным (без завихрений) течениям жидкости по трубке с жесткими неупругими стенками. В частности, в турбулентном режиме разность давлений пропорциональна не кровотоку, а его квадрату и может значительно превышать значения, рассчитанные по формулам ламинарного течения.
Из уравнения (9) видно, что увеличение кровотока может быть достигнуто как повышением градиента давления, так и увеличением внутреннего радиуса трубки. Оба этих механизма регулирования кровотока имеют большое значение в физиологии.
Вводя так называемое гидравлическое сопротивление, в простом случае течения Пуазейля определяющееся формулой
R: = , (2.10)
мы приходим к соотношениям между градиентом давления и кровотоком в сосуде, полностью аналогичным закону Ома для электрического тока
Q= ,или, другими словами, =·(2.11)
где кровоток Q соответствует силе электрического тока I, проходящего по проводнику, а ?P – падению напряжения U на сопротивлении R.
Формулы для электрического и гидравлического сопротивлений также аналогичны, но электрическое сопротивление обратно пропорционально квадрату, а гидравлическое – четвертой степени радиуса трубки.
Заменяя вязкость в (10) ее значением, запишем соотношения (11) между кровотоком и падением давления в отрезке сосуда в следующем виде:
Q =л, т.е. =л-1 Q; (2.12)
л = ? 60 физиол. ед., л-1 ? 0,0166 физиол. ед.
В конкретном примере, когда длина сосуда L =1 см, внутренний радиус r = 1 мм = 0.1 см, по формуле (11) находим, что для поддержания в сосуде кровотока Q =60 мл/мин разность давлений на входе и выходе сосуда должна составлять 1 мм рт. ст.
Основное уравнение гидравлики (11) применимо не только к одиночному сосуду, но и к стационарным течениям в разветвляющейся сети трубок и даже во всей системе кровообращения в целом. При этом оказывается, что эквивалентное гидравлическое сопротивление R* сосудов большого круга составляет около
R* ? 60 физиол. ед. = 133·106 кг/м2·сек. = 133·105г/см2·сек. (2.13)
Гидравлические сопротивления складываются, подобно соединению резисторов в электрических схемах (рис. 2.10), при последовательном соединении; при параллельном же соединении складываются проводимости, т.е. величина, обратная к общему сопротивлению параллельно соединенных трубок равна сумме обратных величин к сопротивлениям отдельных трубок
Рисунок 2.10. Последовательное и параллельное соединение сосудов (гидравлических проводников)
Rпосл= R1 + R2+ …Rп ; (2.14)
В общем случае, сложная сеть артериальных сосудов может являться графом, ребра которого представляют отдельные сосуды, а вершины – узлы, в которых сосуды расщепляются (или сливаются). Сопротивление каждого ребра рассчитывается по формулам (10) или (12).
Выбирая в качестве искомых неизвестных давления Pk в N ? 109 вершинах, через них по уравнению (11) записываем кровотоки во всех сосудах, удовлетворяющие (в стационарном случае) условию баланса: в каждом узле алгебраическая сумма кровотоков равна нулю.
Добавляя сюда те или иные граничные условия (например, задавая величину давления или кровотока в аорте, и приравнивая нулю давление на концах артериол), приходим к системе линейных алгебраических уравнений (СЛАУ). Практическое решение, даже на самом мощном компьютере, получающейся NхNСЛАУ не представляется возможным без дополнительных предположений, например, агрегирования (укрупнения) групп сосудов одного поколения.
На рис. 2.11 лишь левый сердечный насос и главные артерии большого круга кровообращения и последовательно с ними соединенные системы артериол (более узкие прямоугольники). Короткие черточки (как в электрических схемах) указывают на переход к капиллярной и венозной системам, давление в которых очень мало и его можно считать нулевым. Пунктиром помечены части тела, относящиеся к соответствующим участкам АСС.
Через R1, R2, R9, R10, R11 обозначены отрезки восходящей аорты, R3 – R6- коронарные артерии и артериолы, R7, R8 нисходящие ветви аорты R12 – R16 – артерии и артериолы, питающие мозг, R17- R20 – лучевые сосуды рук, R21- R24 сосуды внутренних органов, R25- R28- артериальные сосуды ног.
В табл. 2.1. приведены данные к рис. 2.11, которые будут использоваться в расчетной задаче № 3.
Таблица 2.1. Ориентировочные значения гидравлических сопротивлений (в физиологических единицах)
R1 | 2 | R8 | 20 | R15 | 200 | R22 | 150 |
R2 | 3 | R9 | 3 | R16 | 600 | R23 | 30 |
R3 | 400 | R10 | 2 | R17 | 300 | R24 | 250 |
R4 | 3600 | R11 | 2 | R18 | 1500 | R25 | 100 |
R5 | 400 | R12 | 100 | R19 | 300 | R26 | 700 |
R6 | 3600 | R13 | 100 | R20 | 1500 | R27 | 100 |
R7 | 20 | R14 | 600 | R21 | 20 | R28 | 700 |
Рис. 2.11. Схема укрупненного графа артериальной сосудистой системы человека
Важно учесть также гравитационные силы (отсутствующие лишь в состоянии невесомости), что осуществляется добавлением к давлению Pk в каждой вершине слагаемого phk, где hk высота данной точки над некоторым уровнем (обычно уровнем расположения сердца).
Несмотря на упрощенный характер гидравлического описания, оно дает возможность строить удовлетворительные модели начального приближения.
Источник
Гемодинамика — раздел науки, изучающий механизмы движения крови в сердечно-сосудистой системе. Он является частью гидродинамики раздела физики, изучающего движение жидкостей.
Согласно законам гидродинамики, количество жидкости (Q), протекающее через любую трубу, прямо пропорционально разности давлений в начале (Pi) и в конце (Pi) трубы и обратно пропорционально сопротивлению (R) току жидкости:
Если применить это уравнение к сосудистой системе, то следует иметь в виду, что давление в конце данной системы, т. е. в месте впадения полых вен в сердце, близко к нулю. В этом случае уравнение можно записать так:
где Q — количество крови, изгнанное сердцем в минуту; Р — величина среднего давления в аорте, R — величина сосудистого сопротивления.
Из этого уравнения следует, что Р = Q*R, т. е. давление (Р) в устье аорты прямо пропорционально объему крови, выбрасываемому сердцем в артерии в минуту (Q) и величине периферического сопротивления (R). Давление в аорте (Р) и минутный объем крови (Q) можно измерить непосредственно. Зная эти величины, вычисляют периферическое сопротивление — важнейший показатель состояния сосудистой системы.
Периферическое сопротивление сосудистой системы складывается из множества отдельных сопротивлений каждого сосуда. Любой из таких сосудов можно уподобить трубке, сопротивление которой (R) определяется по формуле Пуазейля:
где / — длина трубки; ч — вязкость протекающей в ней жидкости; л — отношение окружности к диаметру; г — радиус трубки.
Сосудистая система состоит из множества отдельных трубок, соединенных параллельно и последовательно. При последовательном соединении трубок их суммарное сопротивление равно сумме сопротивлений каждой трубки:
При параллельном соединении трубок их суммарное сопротивление вычисляют по формуле:
Точно определить сопротивление сосудов по этим формулам невозможно, так как геометрия сосудов изменяется вследствие сокращения сосудистых мышц. Вязкость крови также не является величиной постоянной. Например, если кровь протекает через сосуды диаметром меньше 1 мм, вязкость крови значительно уменьшается. Чем меньше диаметр сосуда, тем меньше вязкость протекающей в нем крови. Это связано с тем, что в крови наряду с плазмой имеются форменные элементы, которые располагаются в центре потока. Пристеночный слой представляет собой плазму, вязкость которой намного меньше вязкости цельной крови. Чем тоньше сосуд, тем большую часть площади его поперечного сечения занимает слой с минимальной вязкостью, что уменьшает общую величину вязкости крови. Теоретический расчет сопротивления капилляров невозможен, так как в норме открыта только часть капиллярного русла, остальные капилляры являются резервными и открываются по мере усиления обмена веществ в тканях.
Из приведенных уравнений видно, что наибольшей величиной сопротивления должен обладать капилляр, диаметр которого 5— 7 мкм. Однако вследствие того что огромное количество капилляров включено в сосудистую сеть, по которой осуществляется ток крови, параллельно, их суммарное сопротивление меньше, чем суммарное сопротивление артериол.
Основное сопротивление току крови возникает в артериолах. Систему артерий и артериол называют сосудами сопротивления, или резистивными сосудами.
Артериалы представляют собой тонкие сосуды (диаметром 15— 70 мкм). Стенка этих сосудов содержит толстый слой циркулярно расположенных гладких мышечных клеток, при сокращении которого просвет сосуда может значительно уменьшаться. При этом резко повышается сопротивление артериол. Изменение сопротивления артериол меняет уровень давления крови в артериях. В случае увеличения сопротивления артериол отток крови из артерий уменьшается и давление в них повышается. Падение тонуса артериол увеличивает отток крови из артерий, что приводит к уменьшению артериального давления. Наибольшим сопротивлением среди всех участков сосудистой системы обладают именно артериалы, поэтому изменение их просвета является главным регулятором уровня общего артериального давления. Артериалы — «краны сердечно-сосудистой системы» (И. М. Сеченов). Открытие этих «кранов» увеличивает отток крови в капилляры соответствующей области, улучшая местное кровообращение, а закрытие резко ухудшает кровообращение данной сосудистой зоны.
Итак, артериалы играют двоякую роль: участвуют в поддержании
Рис. 7.17. Изменения давления в разных частях сосудистой системы.
-
 — в аорте; 2 — в крупных вртериях; 3 — в мелких артериях; 4 — в вртериолах; 5 — в капиллярах; 6 — в венулах; 7 — в венах; 8 — в полой вене. Штриховкой обозначено колебание давления в систолу и диастолу, пунктиром — среднее давление.
— в аорте; 2 — в крупных вртериях; 3 — в мелких артериях; 4 — в вртериолах; 5 — в капиллярах; 6 — в венулах; 7 — в венах; 8 — в полой вене. Штриховкой обозначено колебание давления в систолу и диастолу, пунктиром — среднее давление.
необходимого организму уровня общего артериального давления и в регуляции величины местного кровотока через тот или иной орган или ткань. Величина органного кровотока соответствует потребности органа в кислороде и питательных веществах, определяемой уровнем рабочей активности органа.
В работающем органе тонус артериол уменьшается, что обеспечивает повышение притока крови. Чтобы общее артериальное давление при этом не снизилось в других (неработающих) органах, тонус арте- рнол повышается. Суммарная величина общего периферического сопротивления н общий уровень артериального давления остаются примерно постоянными, несмотря на непрерывное перераспределение крови между работающими и неработающими органами.
О сопротивлении в различных сосудах можно судить по разности давления крови в начале н в конце сосуда: чем выше сопротивление току крови, тем большая сила затрачивается на ее продвижение по сосуду и, следовательно, тем значительнее падение давления на протяжении данного сосуда. Как показывают прямые измерения давления крови в разных сосудах, давление на протяжении крупных и средних артерий падает всего иа 10%, а в артериолах и капиллярах — на 85%. Это означает, что 10% энергии, затрачиваемой желудочками на изгнание крови, расходуется на продвижение крови в крупных и средних артериях, а 85% — на продвижение крови в артериолах и капиллярах. Распределение давления в разных отделах сосудистого русла показано на рис. 7.17.
Зная объемную скорость кровотока (количество крови, протекающее через поперечное сечение сосуда), измеряемую в миллилитрах в секунду, можно рассчитать линейную скорость кровотока, которая выражается в сантиметрах в секунду. Линейная скорость (V) отражает скорость продвижения частиц крови вдоль сосуда и равна объемной (Q), деленной на площадь сечения кровеносного сосуда:
Линейная скорость, вычисленная по этой формуле, есть средняя скорость. В действительности линейная скорость различна для частиц
Рис. 7.18. Средняя линейная скорость тока крови в разных частях сосудистой системы.
 крови, продвигающихся в центре потока (вдоль продольной оси сосуда) и у сосудистой стенки. В центре сосуда линейная скорость максимальна, около стенки сосуда она минимальна в связи с тем, что здесь особенно велико трение частиц крови о стенку.
крови, продвигающихся в центре потока (вдоль продольной оси сосуда) и у сосудистой стенки. В центре сосуда линейная скорость максимальна, около стенки сосуда она минимальна в связи с тем, что здесь особенно велико трение частиц крови о стенку.
Объем крови, протекающей в 1 мин через аорту или полые вены и через легочную артерию или легочные вены, одинаков. Отток крови от сердца соответствует ее притоку. Из этого следует, что объем крови, протекший в 1 мин через всю артериальную и всю венозную систему большого и малого круга кровообращения, одинаков. При постоянном объеме крови, протекающей через любое общее сечение сосудистой системы, линейная скорость кровотока не может быть постоянной. Она зависит от общей ширины данного отдела сосудистого русла. Это следует из уравнения, выражающего соотношение линейной и объемной скорости: чем больше общая площадь сечения сосудов, тем меньше линейная скорость кровотока. В кровеносной системе самым узким местом является аорта. При разветвлении артерий, несмотря на то, что каждая ветвь сосуда уже той, от которой она произошла, наблюдается увеличение суммарного русла, так как сумма просветов артериальных ветвей больше просвета разветвившейся артерии. Наибольшее расширение русла отмечается в капиллярной сети: сумма просветов всех капилляров примерно в 500—600 раз больше просвета аорты. Соответственно этому кровь в капиллярах движется в 500—600 раз медленнее, чем в аорте.
В венах линейная скорость кровотока снова возрастает, так как при слиянии вен друг с другом суммарный просвет кровяного русла суживается. В полых венах линейная скорость кровотока достигает половины скорости в аорте. Распределение скорости кровотока в кровеносной системе показано на рис. 7.18.
В связи с тем что кровь выбрасывается сердцем отдельными порциями, кровоток в артериях имеет пульсирующий характер, поэтому линейная и объемная скорости непрерывно меняются: они максимальны в аорте и легочной артерии в момент систолы желудочков и уменьшаются во время диастолы. В капиллярах и венах кровоток постоянен, т. е. линейная скорость его постоянна. В превращении пульсирующего кровотока в постоянный имеют значение свойства артериальной стенки.
Непрерывный ток крови по всей сосудистой системе обусловливают выраженные упругие свойства аорты и крупных артерий.
В сердечно-сосудистой системе часть кинетической энергии, развиваемой сердцем во время систолы, затрачивается на растяжение аорты и отходящих от нее крупных артерий. Последние образуют эластическую, или компрессионную, камеру, в которую поступает значительный объем крови, растягивающий ее; при этом кинетическая энергия, развитая сердцем, переходит в энергию эластического напряжения артериальных стенок. Когда систола заканчивается, растянутые стенки артерий стремятся спасаться и проталкивают кровь в капилляры, поддерживая кровоток во время диастолы.
С позиций функциональной значимости для системы кровообращения сосуды подразделяются на следующие группы:
- Упруго-растяжимые — аорта с крупными артериями в большом круге кровообращения, легочная артерия с ее ветвями — в малом круге, т. е. сосуды эластического типа.
- Сосуды сопротивления (резистивные сосуды) — артериады, в том числе и прекапиллярные сфинктеры, т. е. сосуды с хорошо выраженным мышечным слоем.
- Обменные (капилляры) — сосуды, обеспечивающие обмен газами и другими веществами между кровью и тканевой жидкостью.
- Шунтирующие (артериовенозные анастомозы) — сосуды, обеспечивающие «сброс» крови из артериальной в венозную систему сосудов, минуя капилляры.
- Емкостные — вены, обладающие высокой растяжимостью. Благодаря этому в венах содержится 75—80% крови.
Процессы, протекающие в последовательно соединенных сосудах, обеспечивающие циркуляцию (кругооборот) крови, называют системной гемодинамикой. Процессы, протекающие в параллельно подключенных к аорте и полым венам сосудистых руслах, обеспечивая кровоснабжение органов, называют регионарной, или органной, гемодинамикой.
Источник