Поверхность уровня жидкости в сосуде
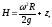
Поверхностью уровня называется поверхность, все точки которой имеют одно и тоже значение рассматриваемой функции. В гидравлике особо важное значение имеет поверхность равного давления. Во всех точках такой поверхности уровня гидростатическое давление одинаково, т.е. р = const и dр = 0, поэтому из уравнения (2.13) следует
,
т.к. плотность жидкости ρ≠0, то
. (2.31)
Формула (2.31) называется уравнением поверхности равного давления.
Поверхность равного давления обладает двумя свойствами.
1. Две поверхности равного давления не пересекаются между собой.
Допустим, что поверхность равного давления р1 пересекается с поверхностью равного давления р2. Тогда в точках линии пересечения этих поверхностей давление было бы одновременно равным и р1 и р2, что невозможно, т.к. р1≠ р2. Следовательно, поверхности равного давления не пересекаются.
2. Внешние объемные силы направлены нормально к поверхности уровня.
Докажем это свойство. По второму закону Ньютона, элементарная работа сил, действующих в жидкости, равна:
.
Согласно формуле (2.31), имеем dA = 0. С другой стороны, из механики твердого тела известно, что
,
где α – угол между вектором силы и направлением движения;
F – сила, действующая на единицу объема жидкости;
dl – элементарный путь.
Так как F≠, dl≠, dA=0, то получаем или . Если жидкость находится только в поле сил земного тяготения, то ускорения X, Y, Z вдоль координатных осей равны: X = , Y = , Z = –g. После подстановки этих значений в уравнение (2.31) имеем
или . (2.32)
Интегрируя выражения (2.32) получаем
или . (2.33)
Уравнения (2.33) представляют собой семейство горизонтальных плоскостей. Следовательно, поверхностью равного давления в поле сил тяжести является горизонтальная плоскость.
ОТНОСИТЕЛЬНОЕ РАВНОВЕСИЕ ЖИДКОСТИ
ВО ВРАЩАЮЩЕМСЯ СОСУДЕ
Относительным равновесием жидкости называется такой случай ее движения, при котором отдельные ее частицы не смещаются одна относительно другой, и вся масса жидкости движется как твердое тело.
Предположим, что цилиндр, наполненный жидкостью до высоты h, приведен во вращательное движение вокруг вертикальной оси OZ с угловой скоростью ω (рис.2.11).
Рис 2.11
Вращающиеся стенки цилиндра приведут во вращение ближайшие к стенкам слои жидкости, а затем, вследствие вязкости жидкости, и всю ее массу. По истечении некоторого времени вся жидкость будет вращаться, примерно стой же угловой скоростью ω, что и сосуд.
Допустим, что такой момент времени наступил. Рассмотрим два интересующих нас вопроса.
1. Какую форму будет иметь поверхность равного давления, и в частности, свободная поверхность?
2. Каков закон распределения гидростатического давления?
Чтобы ответить на поставленные вопросы, рассмотрим уравнение поверхности равного давления (2.31). Для нахождения проекций ускорения выберем в жидкости точку А и покажем ускорения возникающие под действием сил, действующих в жидкости. Силами, действующими в жидкости, являются сила земного тяготения (направленная вертикально вниз по оси OZ) и центробежная сила (направленная вдоль оси ОХ к периферии). В результате действия этих сил полное ускорение точки А будет складываться из ускорения свободного падения g и центробежного ускорения ε.
Составляющие массовых сил, действующих в данном случае на жидкость, X, Y, и Z будут равны:
; ; , (2.34)
где εх, εy – проекции центробежного ускорения по осям х и y.
Подставляя выражения (2.34) в уравнение (2.31) получаем
. (2.35)
После решения уравнения (2.35) относительно dz и его интегрирования получаем
. (2.36)
Постоянную интегрирования С находим из следующих условий: Х = , Y= 0, Z = h*. Следовательно С= h* , т.е. постоянная интегрирования равна глубине залегания самой нижней точки свободной поверхности (вершины параболы).
С учетом постоянной интегрирования С, и при условии, что величина h* определяется из условия неизменности первоначального объема жидкости, т.е.
, (2.37)
уравнение (2.36) принимает вид:
. (2.38)
Полученное уравнение (2.38) является уравнением свободной поверхности жидкости во вращающемся сосуде. Согласно полученному уравнению (2.38), формой свободной поверхности является параболоид вращения.
В уравнении (2.38), x2 + y2= r2, где r – координата рассматриваемой точка А. При условии, что r = R, т.е. рассматриваемая точка А находится на внутренней поверхности вращающегося сосуда, наблюдается максимальный подъем жидкости на высоту zmax. Для определения zmax в уравнение (2.38) подставляем выражение x2 + y2= r2 и получаем
. (2.39)
Согласно полученному уравнению (2.39) можно сделать вывод, что жидкость во вращающемся сосуде поднимается на столько, на сколько и опускается.
Теперь установим закон распределения гидростатического давления.
Подставляя выражения (2.34) в уравнение (2.13) получим
. (2.40)
Выполняя интегрирования уравнения (2.40) получим
. (2.41)
Постоянную интегрирования С находим из следующих условий: Х = 0, Y= 0, Z = h*, р=ратм.
С учетом вышеперечисленного, уравнение (2.41) принимает следующий вид:
(2.42)
или
. (2.43)
Уравнения (2.42) и (2.43) являются уравнениями закона распределения гидростатического давления.
Источник
В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать
различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.
1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции.
Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле
p = p0 + ρ·(g·z ± a·x),
Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:
g·z = ± a·x
или
z/x = tg α = ± a/g,
где α – угол наклона свободной поверхности жидкости к горизонту.
Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l)
высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.
Если сосуд движется равномерно (а = 0), уравнение приводим к виду:
p = p0 + ρ·g·z = p0·γ
В этом случае поверхность равного давления представляет горизонтальную плоскость.
2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.
Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:
p = p0 + γ·((ω2·r2)/(2·g) – z)
Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:
z = (ω2·r2)/(2·g) = u2/(2·g),
где окружная скорость u = ω·r (r — радиус вращения точки).
Высота параболоида вращения:
h = ω2·r20/(2·g),
где r0 – радиус цилиндрического сосуда.
Сила давления жидкости на дно сосуда:
P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),
где h0 – начальная глубина жидкости в сосуде до момента его вращения.
Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).
3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.
В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.
Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).

При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).
Распределение давления по глубине жидкости определяется выражением:
p = p0 + γ·ω2·(r2 – r20)/(2·g)
где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.
Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.
Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в.
Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Источник
6
ЛЕКЦИЯ
2
Уравнение
поверхностей уровня жидкости, вращающейся
вместе с сосудом вокруг вертикальной
оси с угловой скоростью ω. Уравнение
свободной поверхности уровня.
Пусть
имеется сосуд с жидкостью, вращающийся
вокруг вертикальной оси с угловой
скоростью ω. Найдем уравнение поверхностей
уровня для рассматриваемого случая,
воспользовавшись уравнением поверхности
уровня в дифференциальном виде
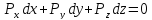 .
.
На
жидкость массой m
в окрестностях произвольно взятой точки
М действуют внешние массовые силы:
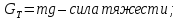
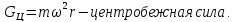 Найдем
Найдем
проекции этих сил и суммы проекций
единичных массовых сил на оси координат.
Ось
x
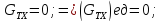
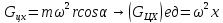 Следовательно,
Следовательно,
сумма проекций единичных массовых сил
на ось x
будет равна
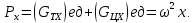

R
– радиус сосуда;
r
– радиус вращения т. М;
h
– глубина погружения т. М от
свободной
поверхности
уровня.
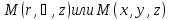
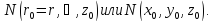
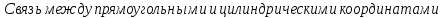
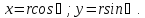
Ось
y
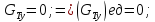
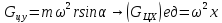
Следовательно,
сумма проекций единичных массовых сил
на ось y
будет равна
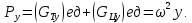 Ось
Ось
z
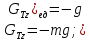
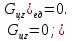 Следовательно,
Следовательно,
сумма проекций единичных массовых сил
на ось z
будет равна
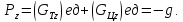
Подставляя
найденные значения сумм проекций
единичных массовых сил, получим
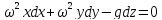 .
.
Берем неопределенный интеграл полученного
выражения
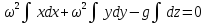
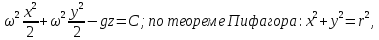
поэтому
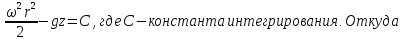
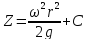
– уравнение
поверхностей уровня
(уравнение семейства параболоидов
вращения)
Уравнение
свободной поверхности уровня
Рассмотрим
вершину параболоида вращения
соответствующего свободной поверхности
уровня; для нее справедливо: r=0;
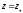 ;
;
подставляя эти значения в последнее
уравнение получим значение константы
интегрирования для уравнения свободной
поверхности уровня
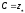 ,
,
отсюда следует что, уравнением свободной
поверхности уровня будет

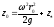
Геометрический
смысл
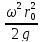
– высота
подъема ветви параболоида вращения
относительно горизонтальной плоскости
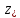
для точки на свободной поверхности
уровня N(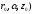 .
.
Максимальная
высота подъема жидкости в сосуде
H
– максимальная высота подъема жидкости
параболоида вращения свободной
поверхности уровня.
Согласно
уравнения свободной поверхности уровня
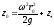
для точки на этой поверхности с
координатами ( )
)
связь между Н и R
будет определяться уравнением
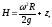 .
.
Далее следует заменить

через первоначальный уровень жидкости
в сосуде
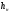 (при
(при
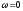 ).
).

– объем
жидкости в сосуде, который находится в
состоянии абсолютного покоя;

–
объем жидкости в сосуде, который находится
в состоянии относительного покоя; в
силу закона сохранения объема жидкости
получают
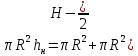
Откуда
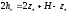
или
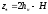 .
.
Подставляя полученное выражение в ранее
найденное для максимальной высоты
подъема жидкости, получим
 ,
,
откуда
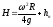
– максимальная
высота подъема жидкости в сосуде
Закон
распределения давления внутри жидкости,
вращающейся вместе с сосудом вокруг
вертикальной оси с угловой скоростью
ω.
Закон
Паскаля ,
,
полученный ранее для случая абсолютного
покоя жидкости, справедлив и для случая
относительного покоя в любых его формах
в том числе и для вращающегося сосуда;
здесь h
есть сумма высоты подъема ветви
параболоида вращения над плоскостью
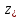
и расстояния между горизонтальными
плоскостями
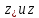 .
.
Т.е.
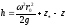 .
.
Определение
силы давления жидкости на плоскую стенку
сосуда и на дно сосуда (без вывода).

РИСУНОК
F
– площадь
смоченной боковой стенки сосуда;
hц
–
глубина
погружения центра масс площади F;
точка
ЦМ
– центр масс площади F;
точка
ЦД
– центр давления, точка приложения
равнодействующей силы давления.
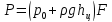
– сила
полного давления на боковую стенку
сосуда (сила атмосферного давления +
сила гидростатического давления
жидкости).
Сила
полного давления на дно сосуда может
быть определена по формуле

Определение
точки приложения силы полного давления
(координаты центра давления
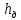 ).
).
Без вывода.
 I
I
– момент инерции площади, относительно
центральной оси (ось, которая проходит
через центр масс площади F)
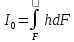
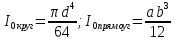 ,
,
где a
– основание прямоугольника, b
– высота.
Элементы
кинематики жидкости
(Основная
теорема кинематики – теорема
Коши-Гельмгольца. Траектория жидкостной
частицы. Линии тока. Элементарная
струйка. Трубка тока. Поток жидкости.
Живое сечение потока. Смоченный периметр.
Гидравлический радиус.
Эквивалентный диаметр).
В
кинематике изучают движение жидкости
с точки зрения геометрии, без учета ее
массы и сил, определяющих это движение
Основная
теорема кинематики – теорема
Коши-Гельмгольца. В этой теореме
доказывают, что скорость перемещения
жидкостной частицы складывается из
трех скоростей:
– поступательная
скорость;
– деформационная
скорость;
Изменение
прямых углов одной из граней за время
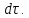
– вращательная
скорость.
Траектория
жидкостной частицы – это путь, пройденный
жидкостной частицей за некоторый
промежуток времени (S).
Линиями
тока называют совокупность жидкостных
частиц, векторы скоростей которых
касательны к ней в данный момент времени.
Элементарная
струйка. Трубка тока.
Если
в движущейся жидкости в поперечном
сечении выделить элементарную площадку
dS
и через все точки провести линии тока
для данного момента времени, то получается
объемный пучок линий тока, который
называется элементарной
струйкой,
а ее боковая поверхность – поверхность
трубки тока.

Поток
жидкости
– это совокупность элементарных струек
жидкости, текущих в данном русле.
Живое
сечение потока
– это поверхность, проведенная через
данную точку в пределах потока,
перпендикулярная линиям тока.
Смоченным
периметром
называют длину линии, по которой жидкость
в данном живом сечении соприкасается
с руслом.
Гидравлический
радиус (для канала с произвольным
сечением)
– это отношение площади живого сечения
к смоченному периметру.
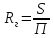
Для
круглой трубы гидравлический радиус
равен:

где
d
– смоченный периметр
Гидравлический
радиус в два раза меньше геометрического.
Эквивалентный
диаметр (для канала произвольного
сечения) принимается равным:
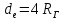

Плавно
изменяющееся движение жидкости
– это такое движение, при котором
кривизна струек мала, угловое расхождение
между отдельными струйками не велико,
живое сечение потока плоское,
перпендикулярно оси потока.
Расход
жидкости – это объем жидкости, протекающей
через поперечное сечение потока в
единицу времени.
Средней
скоростью в данном сечении потока
называется такая фиктивная, но одинаковая
во всех точках данного сечения скорость,
при которой через сечение проходит то
же количество жидкости, какое и при
действительном распределении скоростей.
Источник
Рассмотрим случай равновесия жидкости в состоянии «абсолютного покоя», т.е. когда на жидкость действует только сила тяжести. Поскольку объём жидкости в сосуде мал по сравнению с объёмом Земли, то уровень свободной поверхности жидкости в сосуде можно считать горизонтальной плоскостью. Давление на свободную поверхность жидкости равно атмосферному давле нию р0. Определим давление р в произвольно выбранной точке М, расположенной на глубине h. Выделим
около точки М горизонтальную площадку площадью dS . Построим на данной площадке вертикальное тело, ограниченное снизу самой площадкой, а сверху (в плоскости свободной поверхности жидкости) её проекцией. Рассмотрим равновесие полученного жидкого тела. Давление на основание выделенного объёма будет внешним по отношению к жидкому телу и будет направлено вертикально вверх. Запишем уравнение равновесия в проекции на вертикальную ось тела.
Сократив все члены уравнения на dS, получим:
Давление во всех точках свободной поверхности одинаково и равно р0, следовательно, давление во всех точках жидкости на глубине h также одинаково согласно основному уравнения гидростатики. Поверхность, давление на которой одинаково, называется поверхностью уровня. В данном случае поверхности уровня являются горизонтальными плоскостями.
Выберем некоторую горизонтальную плоскость сравнения, проходящую на расстоянии z0 от свободной поверхности, тогда можно записать уравнение гидростатики в виде:
Все члены уравнения имеют линейную размерность и носят название:
– геометричкская высота,
– пьезометрическая высота
Величина носит название гидростатического напора.
Основное уравнение гидростатики, доказанное на примере жидкости находящейся под действием только сил тяжести, будет справедливо и для жидкости, которое испытывает на себе ускорение переносного движения. Под действием сил инерции переносного движения будет меняться положение свободной поверхности жидкости и поверхностей равного давления относительно стенок сосуда и относительно горизонтальной плоскости. Вид этих поверхностей целиком зависти от комбинации ускорений переносного движения и ускорения сил тяжести. В литературе состояние равновесия жидкости при наличии переносного движения называется относительным покоем жидкости. Любые комбинации ускорений сводятся к двум возможным видам равновесия жидкости
Равновесие жидкости при равномерно ускоренном прямолинейном движении сосуда. Примером может быть равновесие жидкости в цистерне, движущейся с некоторым ускорением а. В этом случае на жидкость будут действовать силы тяжести и сила инерции равномерно укоренного движения цистерны . Тогда равно-
действующая единичная массовая сила определиться как сумма векторов ускорения переносного движения и ускорения свободного падения.
При данных условиях вектор единичной массовой силы переносного движения а будет направлен в сторону противоположную движению цистерны, ускорение свободного падения g, как всегда ориентировано вертикально вниз, т.е. как показано на рисунке. При движении цистерны начальное положение свободной поверхности жидкости изменится. Новое положение свободной поверхности жидкости, согласно основному условию равновесия жидкости будет направлена перпендикулярно вектору , т.к., равнодействующий вектор массовых сил должен быть направлен по внутренней нормали к свободной поверхности жидкости. Наклон свободной поверхности жидкости к горизонтальной плоскости определяется соотношением ускорений
Выберем некоторую точку М расположенную внутри жидкости на глубине под уровнем свободной поверхности (расстояние до свободной поверхности жидкости измеряется по нормали к этой поверхности). В точке М выделим малую площадку параллельную свободной поверхности жидкости. Тогда уравнение равновесия жидкости запишется в следующем виде:
Величину заменим эквивалентной величиной , где h -погружение точки М под уровень свободной поверхности жидкости (измеряется по вертикали). Эти две величины
одинаковы, т.к. . После этих преобразований уравнение равновесия
жидкости в цистерне примет привычный вид, соответствующий записи основного закона гидростатики:
Таким образом, давление в любой точке жидкости будет зависеть только от положения этой точки относительно уровня свободной поверхности жидкости. Поверхности равного давления будут параллельны свободной поверхности жидкости, и иметь такой же уклон
Равновесие жидкости в равномерно вращающемся сосуде. Свободная поверхность жидкости, залитой в цилиндрический сосуд и находящейся под действием сил тяжести примет форму горизонтальной плоскости на некотором уровне относительно дна сосуда. После того как мы приведём сосуд во вращение вокруг его вертикальной оси с некоторой постоянной угловой скоростью со = const, начальный уровень свободной поверхности жидкости изменится: в центре сосуда он понизится, а по краям сосуда повысится. При этом форма свободной поверхности примет явно вид криволинейной поверхности вращения. Это явление объясняется тем, что при вращении сосуда вокруг своей оси жидкость в нём будет испытывать ускорение переносного движения направленное в сторону стенок сосуда. Поскольку равнодействующая двух сил: силы тяжести и центробежной силы должна быть направлена по нормали к свободной поверхности жидкости в каждой точке поверхности, то эта равнодействующая будет иметь, как быль сказано выше, две составляющие соответственно силу тяжести, направленную вертикально вниз и центробежную, направленную в горизонтальной плоскости.
В каждой точке свободной поверхности жидкости АОВ вектор углового ускорения будет направлен под некоторым углом а по отношению к касательной плоскости, проходящей через данную точку свободной поверхности.
Отсюда:
В центре на оси вращения, на расстоянии от дна сосуда будет расположена
самая низкая точка свободной поверхности жидкости, т.е.
Отсюда: свободная поверхность жидкости находящейся в равномерно вращающемся вокруг его вертикальной оси сосуде будет иметь вид параболоида вращения (кривая АОВ-парабола).
Выберем любую точку жидкости на глубине под свободной поверхностью h (в частности точка находится на дне сосуда), тогда давление в ней будет равно:
Этот вывод можно распространить и на более сложные случаи вращения сосуда, наклоняя ось его вращения под углом к горизонту; результат получим тот же, что подтверждает универсальность формулы основного уравнения гидростатики.
2.4. Дифференциальное уравнение равновесия жидкости
После рассмотрения некоторых частных случаев равновесия жидкости рассмотрим общее диф
ференциальное равновесия в самом общем виде. Для этой цели выделим отсек жидкости малых размеров в виде параллелепипеда. Масса жидкости в выделенном объёме:
На боковые грани параллелепипеда действуют силы давления: (на левую и правую грани соответственно): . На переднюю и заднюю грани: , на нижнюю
и верхнюю грани:
Поскольку давление на правую грань больше, то i
По аналогии можно записать силы давления на остальные пары граней.
на переднюю , на заднюю , на нижнюю
, на верхнюю Проекции массовых сил на координатные оси:
на ось ОХ будет на ось ОУ будет
на ось OZ будет Тогда сумма сил действующих вдоль оси ОХ:
сумма сил действующих вдоль оси 07:
сумма сил действующих вдоль оси OZ:
где: , проекции ускорения массовых сил на координатные оси.
После преобразования получим систему дифференциальных уравнений равновесия жидкости:
i i >
2.5. Сообщающиеся сосуды
В своей практической деятельности человек часто сталкивается с вопросами равновесия жидкости в сообщающихся сосудах, когда два сосуда А и В соединены между собой жёстко или гибким шлангом. Сами сосуды (А и В) обычно называются коленами. Такой гидравлический элемент часто используется в различных гидравлических машинах (гидравлические прессы и др.), системах гидропривода и гидроавтоматики, различных измерительных приборах и в ряде других случаев. С
природными сообщаю щимися сосудами человек встречается с давних пор: сообщающимися сосудами больших размеров являются водонасыщенные пласты горных пород с системой колодцев, играющих роль отдельных колен природной гидродинамической системы.
В открытых сообщающихся сосудах, заполненных однородной жидкостью свободный уровень жидкости устанавливается на одном и том же уровне в обоих коленах. Если в коленах сосудов залиты две несмешивающиеся жидкости с различной плотностью, то свободные уровни жидкости в правом и левом коленах устанавливаются на разных высотах в зависимости от соотношения плотностей жидкостей.
Для типичного случая, изображённого на рисунке, запишем уравнение равновесия жидкости относительно уровня раздела жидкостей.
или:
В закрытых сообщающихся сосудах давления на свободную поверхность могут быть шными, тогда уравнение равновесия будет иметь следующий вид:
2.6. Сила давления жидкости па плоскую поверхность, погружённую в жидкость
Согласно основному закону гидростатики величина давления р определяется глубиной погружения точки под уровень свободной поверхности h жидкости и величиной
плотности жидкости р.
Для горизонтальной поверхности величина давления одинакова во всех точках этой поверхности, т.к.:
Отсюда:
Таким образом, Сила давления жидкости на горизонтальную поверхность (дно сосуда) равно произведению площади этой поверхности на величину давления на глубине погружения этой поверхности. На рисунке показан так называемый «гидравлический парадокс», здесь величины силы давления на дно всех сосудов одинаковы, независимо от формы стенок сосудов и их физической высоты, т.к. площади доньев у всех сосудов одинаковы, одинаковы и величины давлений.
Сила давления на наклонную поверхность, погруженную в жидкость. Практическим примером такой поверхности может служить наклонная стенка сосуда. Для вывода урав-
нения и вычисления силы давления на стенку выберем следующую систему координат: ось ОХ направим вдоль пересечения плоскости свободной поверхности жидкости с наклонной стенкой, а ось OZ направим вдоль этой стенки перпендикулярно оси ОХ. Тогда в качестве координатной плоскости XOZ будет выступать сама наклонная стенка. На плоскости стенки выделим малую площадку , которую, в связи с малыми размерами можем считать горизонтальной. Величина давления на глубине площадки будет равна:
где: h – глубина погружения площадки относительно свободной поверхности жидкости (по вертикали).
Сила давления dP на площадку:
Для определения силы давления
на всю смоченную часть наклонной стенки (часть площади стенки сосуда, расположенная ниже уровня свободной поверхности жидкости) необходимо проинтегрировать это уравнение по всей смоченной части площади стенки S .
Интеграл представляет собой статический момент площади S относительно
оси ОХ. Он, как известно, равен произведению этой площади на координату её центра тяжести zc. Тогда окончательно:
Таким образом, сила давления на наклонную плоскую поверхность, погружённую в жидкость равна смоченной площади этой поверхности на величину давления в центре тяжести этой площади. Сила давления на плоскую стенку кроме величины и направления характеризуется также и точкой приложения этой силы, которая называется центром давления.
Центр давления силы атмосферного давления p0S будет находиться в центре тяжести площадки, поскольку атмосферное давление передаётся на все точки жидкости одинаково. Центр давления самой жидкости на площадку можно определить исходя из теоремы о моменте равнодействующей силы. Согласно этой теореме момент равнодействующей
силы относительно оси ОХ будет равен сумме моментов составляющих сил относительно этой же оси.
откуда:
где:- положение центра избыточного давления на вертикальной оси,
– момент инерции площадки S относительно оси ОХ.
Отсюда центр давления (точка приложения равнодействующей силы избыточного давления) расположен всегда ниже центра тяжести площадки. В сучаях, когда внешнней действующей силой на свободную поверхность жидкости является сила атмосферного давления, то на стенку сосуда будут одновременно действовать две одинаковые по величине и противоположные по направлению силы обусловленные атмосферным давлением (на внутреннюю и внешнюю стороны стенки). По этой причине реальной действующей несбалансированной силой остаётся сила избыточного давления.
2.7. Сила давления на криволинейную поверхность, погружённую в жидкость
Выберем внутри покоящейся жидкости криволинейную поверхность ABCD, которая может быть частью поверхности некоторого тела погруженного в жидкость. Построим проекции этой поверхности на координатные плоскости. Тогда в координатной плоскости XOZ проекцией этой поверхности будет плоская поверхность , в координатной
плоскости YOZ — плоская поверхность и в плоскости свободной поверхности
жидкости (координатная плоскость ХОТ) – плоская поверхность . На криволи-
нейной поверхности выделим малую площадку dS, проекции которой на координатные
плоскости будут соответственно . Сила давления на криволинейную поверхность dP будет направлена по внутренней нормали к этой поверхности и может быть представлена в виде:
Горизонтальные составляющие могут быть определены, как силы давления
‘ ‘ – на проекции малой площадки dS на соот-
ветствующие координатные плоскости:
Интегрируя эти уравнения, получим (как в случае с давлением на наклонную поверхность):
Вертикальная составляющая силы давления:
^
Второй интеграл в этом равенстве представляет собой объём образованный рассматриваемой криволинейной поверхностью ABCD и её проекцией на свободную поверхность жидкости . Этот объём принято называть телом давления
Таким образом, горизонтальные составляющие силы давления на криволинейную поверхность равны давлениям на вертикальные проекции этой поверхности, а вертикальная составляющая равна весу тела давления, и силе внешнего давления на горизонтальную проекцию криволинейной поверхности.
Основные уравнения гидростатики широко используются на практике. Примероми могут служить простейшие гидравлические машины – гидравлический пресс, построенный по принципу сообщающихся сосудов и гидравлический аккумулятор.
Гидравлический пресс состоит из двух цилиндров приводного (1) и рабочего (2) со-
единеных между собой трубопроводом и представляет систему сообщающихся сосудов. В приводном цилиндре перемещается плунжер малого диаметра d, в рабочем цилиндре находится поршень с большим диаметром D. Связь между плунжером и рабочим поршнем осуществ ляется через рабочую жидкость, заполняющую гидравлическую систему (сообщающиеся сосуды). Усилие F через рычаг передаются рабочей жидкости.
Сила давления на жидкость под плунжером Р]передаёт жидкости давление р, которое, в свою очередь, передаётся во все точки рабочего поршня.
Тогда сила давления на поверхность рабочего поршеня будет равна’
Таким образом, с помощью гидравлического пресса, приложенная к концу рычага
^ сила, увеличивается в раз.
Источник
