При погружении тела в сосуд с жидкостью
Тема урока: Лабораторная работа №9 «Выяснение условий плавания тела в жидкости».
Цель урока:Проведя необходимые исследования:- выяснить условия, при которых тело плавает в разных жидкостях и при которых тонет в них же;- развивать навыки выполнения необходимых замеров и расчётов, уметь анализировать их и делать выводы;- воспитывать аккуратность при выполнении фронтального эксперимента.
Ход урока:
1. Оргмомент.
2.Проверка домаш задания.Актуализация знаний учащихся: Выявить степень готовности класса к уроку, нацелить учащихся на плодотворную работу, отметить отсутствующих.
– Ребята, так как у нас с вами сегодня необычный урок, то мне хотелось бы и начать его необычно.
Я покажу вам фокус, точнее физический фокус, а вы его разгадаете.
(показываю опыт с картофелем, который утонул в чистой воде, а после того как в воду добавили «волшебные» кристаллики поваренной соли и раствор стал насыщенным, картофель не утонул)
– Ответить на вопрос, почему картофель тонет или плавает поможет наша сегодняшняя работа.
Цель нашего урока – исследования заключается в том, чтобы выяснить при каких условиях тело будет плавать, а при каких тонуть. Что бы исследование было более интересным я предлагаю, сделать его в двух вариантах. Первый с чистой водой, второй с насыщенным раствором соли. В конце работы проверим, действительно ли Архимедова сила зависит от плотности жидкости.
– Для проведения эксперимента нам понадобятся некоторые теоретические знания, которые мы сейчас с вами повторим.
2.Проверка домашнего задания: (работаем по карточкам №1, 2)
1.На всякое тело, погружённое в жидкость, действуют две силы: сила тяжести и Архимедова сила. Отметьте в карточке №1 эти силы и укажите, как ведёт себя тело: плавает или тонет, в зависимости от указанной ситуации.
2.В сосуд с водой опустили два тела равного объёма, но разной плотности (например, сухая сосна и парафин). Используя таблицу плотностей твёрдых тел (страница 50 – 51 учебника), нарисуйте в карточке №2 на сколько будут эти тела погружены в воду.
3.Какую исследовательскую работу вы провели дома и что можете сказать о плавание тел? (Учащиеся делают небольшие сообщения о плавание тел)
3.Проведение инструктажа по технике безопасности при работе с лабораторным оборудованием.
– Ребята при выполнении лабораторной работы вы должны помнить:
– нельзя рабочий стол загружать лишними вещами,
– работайте аккуратно, чтобы не разлить жидкость из сосудов,
– пользуйтесь салфеткой для вытирания поплавка от лишней влаги,
– если насыщенный раствор поваренной соли попал на кожу, обязательно помойте это место с мылом,
– выполняя замеры по определению объёма жидкости, совмещайте уровень глаз с уровнем жидкости, для получения более точных результатов,
– поплавок в сосуд с жидкостью опускайте аккуратно, держа его за ниточку, стараясь не расплескать жидкость и не разбить сосуд,
– в случае непредвиденной ситуации немедленно дайте об этом знать учителю.
– Ребята работа выполняется на предложенных вам листах – исследования. Подпишите свои работы в указанном месте и обязательно отметьте, с какой жидкостью вы работаете.
4.Краткий анализ работы.
– Изучение теоретического материала работы.- Приготовление оборудования согласно указаний учебника.- Выполнение работы по указаниям к работе с дополнением того, что одна группа выполняет работу с чистой водой, а другая группа выполняет работу с насыщенным раствором соли.- Выводы к полученным результатам исследования.
5.Самостоятельная работа учащихся.
– Методические рекомендации и индивидуальная помощь учащимся по мере необходимости.
– Контроль за соблюдением техники безопасности.
– По мере выполнения работы делаем записи на доске в приготовленной таблице.
– Делаем вывод о полученных условиях плавания тел и сравниваем результаты для чистой воды и насыщенного раствора соли.
6.Домашнее задание:
Повторить § 50, карточки с индивидуальными разноуровневыми домашними задачами.
Приложение 1
Лист исследования _______________________
Лабораторная работа № 9Тема: Выяснение условий плавания тела в жидкости
Цель работы — на опыте выяснить условия, при которых тело плавает и при которых тонет, как Архимедова сила зависит от плотность жидкости.
Приборы и материалы: измерительный цилиндр (мензурка), пробирка-поплавок с пробкой, сухой песок, бумажная салфетка, вода или насыщенный раствор соли (нужное подчеркнуть).
Указания к работе
1. Насыпьте в пробирку первую порцию песка, чтобы она, закрытая пробкой, плавала в мензурке с жидкостью в вертикальном положении и часть ее находилась над поверхностью воды.
2. Определите выталкивающую силу, действующую на пробирку. Она равна весу воды, вытесненной пробиркой. Для нахождения этого веса определите сначала объем вытесненной воды. Для этого отметьте уровни воды в мензурке до и после погружения пробирки в жидкость. Зная объем вытесненной жидкости и плотность, вычислите ее вес.
3. Выньте пробирку из жидкости, протрите ее фильтровальной бумагой . Зная массу пробирки с песком с точностью до 1 г, рассчитайте силу тяжести, действующую на нее, она равна весу пробирки с песком в воздухе.
4. Насыпьте в пробирку вторую порцию песка. Вновь определите выталкивающую силу и силу тяжести. Проделайте это несколько раз, пока пробирка, закрытая пробкой, не утонет.
5. Результаты измерений и вычислений занесите в таблицу 1 и 2. Отметьте, когда пробирка плавает и когда тонет .
Таблица 1
№ опыта | Объём жидкости до погружения в неё тела | Объём жидкости вместе с телом | Объём погружённого тела |
1 | |||
2 | |||
3 |
Таблица 2
№ опыта | Выталкивающая сила, действующая на пробирку, F, Н, F=g ρ V | Вес пробирки с песком Р, Н, P=g m | Поведение пробирки в воде (плавает или тонет) |
1 | |||
2 | |||
3 |
6. Вывод:
Приложение 2
Карточка №1
Тело тонет Тело плавает Тело всплывает
внутри жидкости
_____________________________________________________________________________
Карточка №2
Источник
Явление при котором тело в силу действия выталкивающей силы, направленной вверх, не тонет при погружении в жидкости или газы — называют плавучестью. Выталкивающая сила является при этом уравновешивающей силой, которая действует противоположно силе тяжести. Здесь стоит отметить, что в качестве среды погружения может выступать не только жидкость, а также и газ, и даже металл!
Плавающие объекты на воде, под водой, в воздухе: корабли, подводные лодки и воздушные шары совершают свое движение благодаря балансу сил тяжести и выталкивания. Традиционно мы попытаемся простым языком без погружения в дремучие формулы объяснить природу плавучести предметов.
- Закон архимеда и плавание тел
- Погружение тела в воду
- Природа выталкивающей силы
- Почему тело плавает?
- Зависимость плавучести от плотности тела

Закон архимеда и плавание тел
Любое тело на Земле падает вниз под воздействием силы тяготения и возникшей соответствующей силы тяжести, направленной вниз. Но, наверняка, все мы замечали, что при погружении предмета в воду — он становится легче. Значит, при погружении предметов в жидкости начинает действовать некая другая сила выталкивающего характера, направленная противоположно силе тяжести вверх.
Выталкивающая сила, противодействующая силе тяготения, называется архимедовой, в честь известного греческого ученого Архимеда, жившего в III веке до нашей эры. Согласно закона Архимеда, на любое тело, погруженное в жидкость, действует выталкивающая сила, величина которой эквивалентна весу тела.
Погружение тела в воду
Масса груши не изменяется при погружении в жидкость, но ее вес уменьшаеся на значение выталкивающей силы со стороны воды.
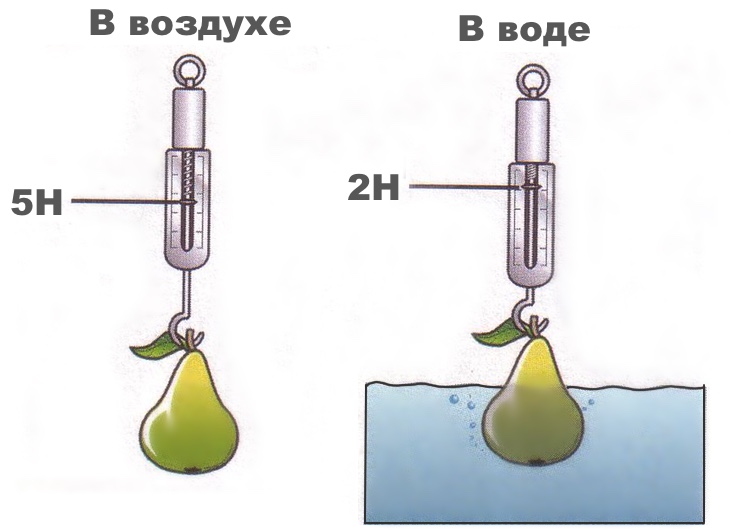
Далее представим себе куб бетона, масса которого составляет 3000 кг или 3 тонны. Из начального курса физики мы получаем вес (масса куба умноженная на ускорение свободного падение h=9,8) бетонного куба. Грубо это величина массы умноженная на 10. Итак вес бетонного куба P = 30000Н (Ньютон). Так вот, при погружении в воду данного объема бетона выталкивается вода массой 1000 кг или 1 тонна.
Противодействующая весу бетонного куба выталкивающая сила равна 10000Н. Именно на эту величину в конечном итоге уменьшается вес куба при полном погружении в воду. 30000Н-10000Н=20000Н. В этом и кроется весь эффект уменьшения веса тема ощущаемой нами под водой. Как видим из нашего эксперимента, при погружении тело потеряло одну третью часть своего веса.
Природа выталкивающей силы
Тела погруженные в любую текучую среду испытывают давление, направленное со всех сторон этой самой среды и величина которого увеличивается по мере погружения. Соответственно давление, которое оказывает среда на тело с неким перепадом высот, будет максимальным в нижней точки (плоскости) тела, а минимальным — в верхней. Направление сил давления на верхнюю плоскость и нижнюю соответственно противоположные.
Результирующая этих двух противоположных по направлению сил и является выталкивающей силой.
Возвращаясь к нашему бетонному кубу, погруженного, к примеру, на глубину 1 м, на него действует силы давления со стороны воды с шести сторон. Посколько боковые стороны куба находятся на одинаковой глубине, то результирующих силы уравновешивает направленные друг к другу силы. Что же относительно сил давления на нижнюю и верхнюю плоскость? Здесь на верхнюю плоскость куба величина силы, направленная вниз, равна 10000Н, а на нижнюю плоскость направлена вверх сила величиной 20000Н. Выталкивающая сила равна разности сил действующих между нижней и верхней — 10000Н.
Почему тело плавает?
Плавающее тело, например судно, выталкивает объем воды из того пространства, ровно которое оно занимает вместо воды. Вес выталкиваемого объема воды равен весу судна. Плавучесть тела объясняется давлением воды.
Многие из нас задаются вопросом почему одни и те же тела с одинаковым объемом плавают, а другие нет, то есть тонут. Вышеупомянутый куб бетона в воде однозначно утонет, а вот куб древесины будет оставаться на плаву. Давайте возьмем деревянный куб массой 500 кг. Его вес составляв 5000Н. Согласно закона Архимеда деревянный куб вытеснит такой же объем воды, как и куб бетона — 1 м3. Масса вытесненной воды останется также неизменной — 1000 кг или 1 тонна. Оказывается плавучесть деревянного куба обусловлена тем, что результирующая выталкивающая сила больше чем вес древесины. Все просто, не так ли?
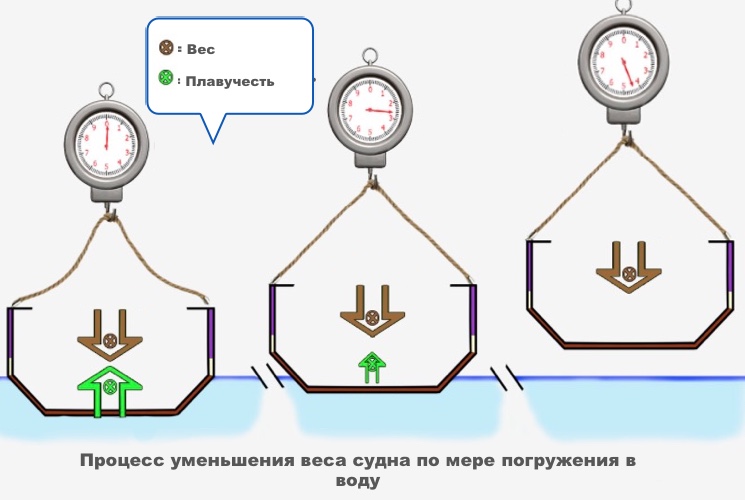
Но как на счет того, что плавающее тело, в частности наш деревянный куб, не полностью, а лишь частично погружен в воду? И воды при этом выталкивается на 1000 кг, а меньше. Этот эффект говорит как раз о уравновешивании выталкивающей силы и веса тела. Под водой находится та часть тела, которая способна создать силу выталкивания равной весу тела, находящегося над водой. Такой баланс сил и отвечает на вопрос почему тело плавает. Если начать сверху добавлять вес к плавающему телу, то объем вытесняемой жидкости растет с его выталкивающей силой растет прямо ровно на величину добавляемого веса. Как результат можно наблюдать все большее погружение тела под воду.
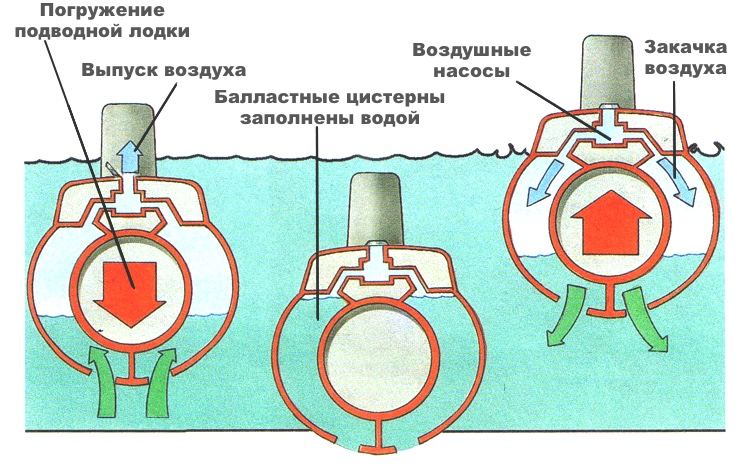
Подводная лодка состоит из водонипроницаемого корпуса, под обшивкой которого расположены цистерны с балластом. При заполненных водой цистернах лодка погружается. Под водой лодка находися во взвешенном состоянии — она не тонет и не всплывает. Когда необходимо всплыть, в балластные цистерны закачивается воздух, который вытесняет воду наружу.
Отметки на борту судна показывают, сколько груза оно способно принять для безопасного плавания. Степень погруженности судна зависит, в частности, от плотности воды, в которой оно находится.
Зависимость плавучести от плотности тела
Итак, мы выяснили, что в зависимости от того будет ли выталкивающая сила больше или меньше веса тела, является свойство его плавучести.
Если выталкивающая сила больше — тело плавает, если меньше — тонет.
Прямой связью того, будет ли тело плавать, является отношением плотности среды к плотности тела, погружаемого в эту самую среду (жидкую или газовую). Вспоминаем курс физики, — плотность тела есть отношение его массы к объему. В наших экспериментах были использовались такие вещества с соответствующими плотностями: бетон — 3000 кг/м3, дерево — 500 кг/м3 и вода 1000 кг/и3. А как же корабли, которые в большей своей массе сделаны из металлов, плотность которых существенно превышает плотность воды?
Здесь стоит помнить, что металлическая часть кораблей это лишь его каркас с элементами усиления, а внутри все остается полым (воздухом).
И в результате в расчетную часть плотности входит этот самый объем воздуха полой части. В итоге результирующая часть выталкивающей силы больше веса тела.
Ареометр — прибор для измерения плотности жидкости. Чем больше плотность жидкости, тем больше выталкивающая сила, и тем выше всплывает корпус прибора.

Все вышеописанное касается не только жидких сред, но и газовых. Возьмем всеми любимые воздушные шары. Они тоже плавают, но только в воздухе. Воздух нагретый горелкой внутри шара имеет меньшую плотность, чем окружающий воздух меньшей температуры. В результате воздушный шар отрывается от земли. Что жа на счет волшебства моментально взлетающих шаров, наполненных газом под названием гелий? Здесь опять же все дело в разности плотности газов гелия и воздуха. Плотность гелия меньше воздуха, поэтому лини с легкостью взлетают на праздничные мероприятия в воздух.
Загрузка…
Источник
Тело впёрнутое в воду, выпирает из воды, силой выпертой воды, телом впёрнутой туды. Такое шутливое стихотворение про Архимедову силу. Силу, которая выталкивает твёрдое тело помещённое в жидкость или газ.
Что заставляет неподвижный предмет с плотностью, меньшей воды, находящийся на дне – всплыть?
Сусанна Казарян, США, Физик
То что предмет всплывает из-за дядюшки Архимеда, догадываюсь знает и автор вопроса. Более интересным является проблема – почему предмет до всплытия был неподвижен на дне? На поверхности видны две версии происходящего.
- Версия 1: Предмет был неподвижен под водой, потому что был приклеен ко дну. Согласно закону Мерфи — “если неприятность может случиться, то она обязательно случается”, и клей со временем растворился в воде, перестав удерживать предмет. Ну а дальше — Архимед.
- Версия 2. Между нижней плоскостью предмета и дном каким-то способом образовался вакуум, т.е предмет как бы “присосался” ко дну. Тогда неподвижность предмета на дне объясняется атмосферным давлением. Согласно того же Мерфи — “если неприятность не может случиться, то она все равно случается”, и вода со временем проникнув под предмет разбудила дядюшку Паскаля, который выровнял атмосферное давление под и над предметом. Ну а дальше — Архимед.
- Версию вмешательства Копперфильда в данный эксперимент не рассматриваю, из-за большой занятости маэстро.
Прочитать ещё 1 ответ
Объясните чайнику: если до Большого взрыва Вселенная была бесконечно мала, то как называлось то пространство, которое ее окружало?
PhD, senior scientist AI, неандерталец
Разум цепляется за привычное. Например, мы привыкли, что все тела падают вниз. Привыкли настолько, что в Англии, на родине Ньютона, еще в девятнадцатом веке огромной общественной популярностью пользовалась книга, в которой «доказывалось», что Земля — плоская, ведь иначе мы бы с нее упали. Раз она плоская, у нее должен быть край. Однако, путешествие Магеллана показало — если плыть все время на запад, то снова приплывешь в Европу, только уже с востока. Итак, Земля — шар, а с тем, что люди на другой стороне ходят «вверх ногами», придется смириться, хоть это и противоречит «здравому смыслу».
Ну, «здравый смысл» с тех пор кое-как примирился с законом всемирного тяготения, но теперь есть новая задача — понять, как Вселенная может быть ограниченной в объеме и при этом не иметь «краев» и чего-то «вне». Что ж, лучшая аналогия — это старые игры, где, выходя за конец экрана, какой-нибудь пэкмен, или диггер, или змейка, или Марио оказывались с противоположного. Для них, таким образом, края экрана не существовало.
Ограниченная по объему трехмерная вселенная — это нечто подобное. Представьте себе: вы находитесь в комнате, у которой как будто две двери в противоположных стенах. Вы открываете дверь и видите такую же комнату и себя со спины, открывающего дверь в следующей стене, за которой видна еще одна комната и еще один вы, и так далее. И за спиной у вас скрипнула дверь — на самом деле та же самая, потому что дверь — одна. И происходит это не потому, что существует бесконечное число вас, а потому что вселенная зациклена сама на себя — просто свет делает несколько кругов по этой вселенной прежде чем достичь ваших глаз. Если в этой нашей вселенной сделать скорость света, к примеру, один метр в секунду, то вы будете видеть себя в другой комнате уже с задержкой в несколько секунд. Теперь добавим еще двери, точнее, одну дверь двум другим стенам комнаты. А теперь — люк в полу и потолке с теми же эффектами.
А теперь — уберем стены, пол и потолок! И увидим многократные копии себя же через равные промежутки пространства. Хотя на самом деле эти копии настолько же реальны, насколько ваше отражение в зеркале — то, что мы видим в зеркале отраженную комнату, отнюдь не значит, что есть еще одна комната.
Поздравляю! Вот вы и очутились во вселенной с ограниченным объемом, но без краев и чего-то «вне». Это лишь один из вариантов, тороидальный. В сферической вселенной вы бы видели размытый образ себя во всем поле зрения — причем, считая, что угол обзора у нас 180°, вы бы видели в упор свой затылок, а в нижнем краю зрения — макушку, в верхнем — подошвы обуви, а по бокам — уши. Но это уже мелочи.
Почему так не происходит в нашей Вселенной? Дело в том, что она расширяется, и достаточно удаленные ее участки улетают от нас быстрее скорости света. В общем, даже если вселенная конечна, свет, испущенный нами или отраженный от нас, просто не имеет возможности к нам возвратиться. Это — большой вариант комнаты.
А теперь рассмотрим противоположный сценарий. Будем сжимать нашу комнату без стен. Вот нам уже в ней неуютно. Вот вы в нее уже не помещаетесь, вас прижимает носом к своему собственному затылку, который вы видите перед собой, и вы чувствуете затылком, как к нему прижало ваш же нос. Вот комната становится размером с атомное ядро… И вот мы приходим в состояние «сразу» после Большого Взрыва. «Сразу» заключено в кавычки, потому что время — это тоже лишь измерение пространства. Так что нет не только «вне» вселенной, но и «до» Большого Взрыва. Ну, то есть, в одной из моделей.
Вот, как-то так.
Прочитать ещё 67 ответов
Источник
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Закон Архимеда
На погружённое в жидкость или газ тело действует выталкивающая сила, и равная весу среды, объём которой равен объёму тела.
Выталкивающая сила (сила Архимеда) равна
[F_A=rho_text{ж} g V_text{пчт}] где (displaystyle V_text{пчт}) — объём погружённой части тела, (displaystyle rho_text{ж}) — плотность жидкости.
Плавание тел
Рассмотрим тело плотности (rho) и жидкость плотности (rho_0). Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести (mg) и архимедова сила (F_A). Если объём тела равен V, то
[mg=rho g V,] [F_A=rho_0 g V]
Имеются три возможности дальнейшего движения тела.
Сила тяжести больше архимедовой силы: (displaystyle mg > F_A), или (displaystyle rho>rho_0). В этом случае тело тонет.
Сила тяжести равна архимедовой силе: (displaystyle mg = F_A), или (displaystyle rho=rho_0). В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
Сила тяжести меньше архимедовой силы: (displaystyle mg < F_A), или (displaystyle rho<rho_0). В этом случае тело всплывает, достигая поверхности жидкости.
Таким образом, условие плавания тела можно записать в виде неравенства (displaystyle rholeq rho_0).
Два жестко связанные друг с другом одинаковых бруска, имеющие толщину (h=5) см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.) 
Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
(displaystylerho_1) – плотность материала, из которого изготовлены бруски, а (displaystyle V) – объем двух брусков. Тогда масса этих брусков будет равна [displaystyle m=rho_1V] Сила, с которой льдинки действуют на воду, равна силе тяжести [displaystyle F=mg=rho_1Vg] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда [F_text{Арх}=rho gfrac{V}2,] где (displaystyle rho) – плотность воды, (displaystyle frac{V}2) – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: [rho_1Vg=rho gfrac{V}2,] откуда (displaystyle rho_1=dfrac{rho}2,) то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину [frac72h=3,5cdot5text{ см}=17,5 text{ см}.] Глубина увеличится на (displaystyle 17,5 -5=12,5) см.
Ответ: 12,5
Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна (displaystyle rho_text{ ал}=2700 text{ кг}/text{м}^3. ) Какова длина ребра куба, если выталкивающая сила равна (displaystyle F_text{Арх}=33,75text{ Н}?) (Ответ дайте в сантиметрах.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV,] где (displaystyle rho_text{в}) – плотность жидкости, в которую погружен кубик, (displaystyle V) – объем погруженной части тела. Так как куб погружен целиком, то (displaystyle V=a^3), получим: [F_text{Арх}=rho_text{в} ga^3] Выразив из этой формулы сторону (displaystyle a), получаем [a=sqrt[3]{frac{F_text{Арх}}{rho_text{в}g }}] Подставив значения в формулу, получим: [a=sqrt[3]{frac{33,75text{ Н}}{10text{ м}/{c^2}cdot1000text{ кг}/text{м}^3}}=0,15text{ м}=15text{ cм }]
Ответ: 15
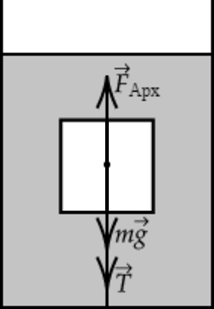
Однородный цилиндр, изготовленный из материала плотностью (displaystyle rho=600) кг/м(^3), с радиусом основания (displaystyle R=25) см и высотой (displaystyle H=20) см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)


Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: [vec T+vec F_text{Арх}+mvec g=mvec a,] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [T- F_text{Арх}+mg=0, quad(1)] массу цилиндра можно рассчитать, исходя из формулы (displaystyle rho=frac {m}{V} Rightarrow m=rho V,) где V – объем цилиндра, который можно вычислить по формуле [V=pi R^2 H] Из формулы (1) выразим силу натяжения нити T:[T=F_text{Арх}-mg=rho_text{в}gV-rho gV=Vg(rho_text{в}-rho)=pi R^2 Hg(rho_text{в}-rho),] где (displaystyle rho_text{в}) – плотность воды, подставим в получившееся выражение численные значения:[T=3,14cdot0,25^2text{ м}cdot0,2text{ м}cdot 10text{ м}/text{с}^2 cdot (1000text{ кг}/text{м}^3-600text{ кг}/text{м}^3)=157text{ Н }]
Ответ: 157
Однородный кубический предмет с ребром (displaystyle a=18) см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна (displaystyle rho_text{др}=340) кг/м(^3), плотность эфира (displaystyle rho_text{э}=720) кг/м(^3). (Ответ дайте в сантиметрах.)
Запишем условие равновесия кубика на поверхности эфира: [F_text{ Арх}=mg, quad(1)] где (F_text{ Арх}) – выталкивающая сила, действующая на брусок, (displaystyle m) – масса кубика, которую можно рассчитать, исходя из формулы (displaystyle rho_text{др}=frac {m}{V} Rightarrow m=rho_text{др} V,) где V – объем кубика, который можно вычислить по формуле [V=a^3.] Выталкивающая сила равна: [F_text{ Арх}=rho_text{э}gV_text{пчт},] где (displaystyle V_text{пчт}) – объем погруженной части кубика,[V_text{пчт}=xa^2,] где (displaystyle x) – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: [rho_text{э}gxa^2=rho_text{др}a^3] [rho_text{э}x=rho_text{др}a, text{ выразим } x=frac{rho_text{др}a}{rho_text{э}}.] Пусть (displaystyle y) – длина части стороны, находящейся над эфиром, можем записать: [y=a-x,] искомая разница длин (displaystyle delta=y-x=a-2x=a-2cdot dfrac{rho_text{др}a}{rho_text{э}}=a(1-2cdot dfrac{rho_text{др}}{rho_text{э}})) подставим в получившееся выражение численные значения: [displaystyle delta=0,18text{ м}(1-2cdot dfrac{340text{ кг}/text{м}^3}{720text{ кг}/text{м}^3})=0,01text{ м}=1text{ см}]
Ответ: 1
В некий резервуар было налито 1000 литров жидкости плотностью (displaystyle rho_1=1500) кг/м(^3). В этой жидкости в равновесии плавает кубик, погруженный в воду на (displaystyle x=130) см. Длина стороны кубика равна (displaystyle a=200) см. В сосуд доливают ещё 1000 литров жидкости плотностью (displaystyle rho_2=1100) кг/м(^3) и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)
В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. [rho_text{нов}=dfrac{rho_1+rho_2}{2}] Так как кубик плавает на поверхности, то можно записать: [mg=F_text{Арх},] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна:[F_text{Арх1}=rho_1 g V_text{пчт1},] где (displaystyle V_text{пчт1}=a^2x) – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: [F_text{Арх2}=rho_text{нов} g V_text{пчт2}=dfrac{rho_1+rho_2}{2}g V_text{пчт2},]где (displaystyle V_text{пчт2}=a^2y) – объем погруженной части куба до смешивания, (displaystyle y) – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим [rho_1 g a^2x=dfrac{rho_1+rho_2}{2} g a^2y] [rho_1x=dfrac{rho_1+rho_2}{2}y,] выразим отсюда y: [y=frac{2rho_1 x}{rho_1+rho_2},] подставим в получившееся выражение численные значения: [y=frac{2cdot1500text{ кг}/text{м}^3 cdot1,3text{ м}}{1500text{ кг}/text{м}^3+1100text{ кг}/text{м}^3}=1,5text{ м}]
Ответ: 1,5
Стеклянный шарик опускается в воде с ускорением (displaystyle a=6) м/с(^2). Найти плотность стекла. Плотность воды (displaystyle rho_text{в}=1000) кг/м(^3). Силами вязкого трения пренебречь. (Ответ дайте в кг/м(^3).)
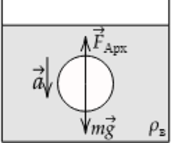
При движении шарика в воде на него действует сила тяжести (displaystyle mvec g) и сила Архимеда (displaystyle F_text{Арх}). Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: [vec F_text{Арх}+mvec g=mvec a,] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [mg- F_text{Арх}=ma,] Отсюда с учетом выражения для силы Архимеда (displaystyle F_text{Арх}=rho_text{в} g V), где V – объем шарика, а
(displaystyle rho_text{в}) – плотность воды, получим: [mg- rho_text{в} g V=ma,] Выразим массу шарика:[m=frac{rho_text{в} g V}{g-a}.] Исходя из формулы, плотность стекла равна [displaystyle rho_text{ст}=frac {m}{V}=frac{rho_text{в} g V}{(g-a)V}=frac{rho_text{в} g }{g-a},] подставим в получившееся выражение численные значения: [rho_text{ст}=frac{1000 text{ кг}/text{м}^3cdot 10text{ м}/text{с}^2 }{10text{ м}/text{с}^2-6text{ м}/text{с}^2}=2500text{ кг}/text{м}^3]
Ответ: 2500
Однородный шарик, изготовленный из материала плотностью (displaystyle rho=2000) кг/м(^3) погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
(displaystyle F_text{Арх}=100) Н? (Ответ дайте в сантиметрах и округлите до целых.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV_text{пчт},] где (displaystyle rho_text{в}) – плотность воды, (displaystyle V_text{пчт}) – объем погруженной части тела. Так как шар полностью опущен в воду, то [V_text{пчт}=frac43pi R^3,] где (displaystyle R) – радиус шара, получим: [F_text{Арх}=rho_text{в} gfrac43pi R^3, (1)] выразим из формулы R: [R=sqrt[3]{frac{3F_text{Арх}}{4rho_text{в}gpi}}] Подставив значения в формулу, получим: [R=sqrt[3]{frac{3 cdot100text{ Н}} {4 cdot1000 text{ кг}/text{м}^3cdot10text{ м}/{c^2}cdot3,14}} approx0,13text{ м}=13text{ см }]
Ответ: 13
Источник
