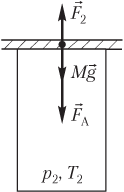При сжатии поршня в сосуде с газом

5.4. Практическое применение уравнения состояния идеального газа
5.4.3. Уравнение состояния для газа, находящегося в сосуде под поршнем
Для идеального газа, находящегося в сосуде под поршнем, необходимо учитывать следующее:
- масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:
m = const;
- постоянным остается также количество вещества (газа):
ν = const;
- плотность газа и концентрация его молекул (атомов) изменяются:
ρ ≠ const, n ≠ const.
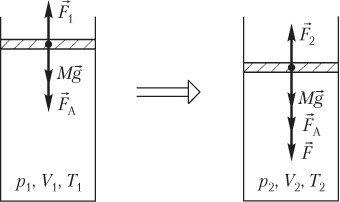
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F→ (рис. 5.9).
Рис. 5.9
Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:
p1V1=νRT1,p2V2=νRT2,}
где p
1, V
1, T
1 — давление, объем и температура газа в начальном состоянии; p
2, V
2, T
2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:
Mg+FA=F1,Mg+FA+F=F2,}
где M — масса поршня; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; S — площадь сечения поршня; F
1 — модуль силы давления газа на поршень в начале процесса, F
1 = p
1S; p
1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F
2 — модуль силы давления газа на поршень в конце процесса, F
2 = p
2S; p
2 — давление газа в сосуде в конечном состоянии.
Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:
- если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —
T ≠ const;
- если процесс происходит медленно, то температура газа остается постоянной –
T = const.
Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:
- если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
- в остальных случаях давление газа под поршнем изменяется — p ≠ const.
Масса поршня, закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:
- если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —
M = 0;
- в остальных случаях поршень обладает определенной ненулевой массой —
M ≠ const.
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм2 и массой 1,80 кг находится 360 см3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см3. Температура газа при его сжатии не изменяется. Определить массу гирь.
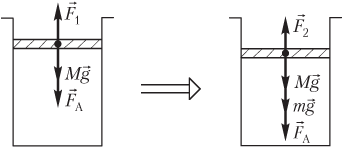
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→1, действующая со стороны газа (до его сжатия);
- сила давления газа F→2, действующая со стороны газа (после его сжатия);
- mg→ — вес гирь.
Условие равновесия поршня запишем в следующем виде:
- до сжатия газа —
F
1 = Mg + F
A,
где F
1 — модуль силы давления газа, F
1 = p
1S; p
1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; g — модуль ускорения свободного падения;
- после сжатия газа —
F
2 = Mg + F
A
+ mg,
где F
2 — модуль силы давления газа, F
2 = p
2S; p
2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.
Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:
- до его сжатия —
p
1V
1 = νRT,
где V
1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- после его сжатия —
p
2V
2 = νRT,
где V
2 — объем сжатого поршнем газа.
Равенство
p
1V
1 = p
2V
2
и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:
p1S=Mg+pAS,p2S=Mg+pAS+mg,p1V1=p2V2,}
которую требуется решить относительно массы гирь m.
Для этого выразим отношение давлений p
2/p
1 из первой пары уравнений:
p2p1=Mg+pAS+mgMg+pAS
и из третьего уравнения:
p2p1=V1V2,
запишем равенство правых частей полученных отношений:
Mg+pAS+mgMg+pAS=V1V2.
Отсюда следует, что искомая масса определяется формулой
m=(M+pASg)(V1V2−1).
Вычисление дает результат:
m=(1,80+100⋅103⋅250⋅10−610)(360⋅10−6240⋅10−6−1)=2,15 кг.
Указанное сжатие газа вызвано гирями массой 2,15 кг.
Пример 20. Открытый цилиндрический сосуд сечением 10 см2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?
Решение. На рисунке показаны силы, действующие на пластину после нагревания газа:
- сила тяжести пластины Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→2, действующая на пластину со стороны нагретого газа.
Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:
F
2 = Mg + F
A,
где F
2 — модуль силы давления нагретого газа, F
2 = p
2S; p
2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление.
Запишем уравнение Менделеева — Клапейрона следующим образом:
- для газа в сосуде до его нагревания
p
1V = νRT
1,
где p
1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p
1 = p
A; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);
- для газа в сосуде после его нагревания
p
2V = νRT
2,
где p
2 — давление нагретого газа; T
2 — температура нагретого газа.
Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:
pAV=νRT1,p2V=νRT2,p2S=Mg+pAS;}
систему необходимо решить относительно температуры T
2, до которой следует нагреть газ.
Для этого делением первой пары уравнений
pAVp2V=νRT1νRT2
получим выражение для давления нагретого газа:
p2=pAT2T1
и подставим его в третье уравнение системы:
pAT2ST1=Mg+pAS.
Преобразуем полученное выражение к виду
T2=T1(Mg+pAS)pAS=T1(MgpAS+1),
а затем найдем разность
ΔT=T2−T1=MgT1pAS.
Произведем вычисление:
ΔT=1,2⋅10⋅300100⋅103⋅10⋅10−4=36 К=36 °С.
Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.
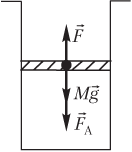
Решение. На рисунке показаны силы, действующие на поршень:
- сила тяжести поршня Mg→;
- сила атмосферного давления F→A;
- сила давления газа F→, действующая на поршень со стороны нагретого газа.
Под действием указанных сил, направленных вверх, поршень движется с ускорением a→:
F→+F→A+Mg→=ma→,
или в проекции на вертикальную ось —
F − F
A − Mg = Ma,
где F — модуль силы давления газа под поршнем, F = pS; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.
Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:
a=F−FA−MgM=(p−pA)SM−g.
Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением
l=v22a,
где l — пройденный путь; v — модуль скорости поршня.
Выразим отсюда модуль скорости поршня:
v=2al
и подставим в записанную формулу выражение для модуля ускорения:
v=2l((p−pA)SM−g).
Выполним расчет:
v=2⋅3,75((450−100)⋅103⋅50⋅10−475,0−10)≈10 м/с.
После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.
Источник
2017-10-05 ![]()
Расположенный горизонтально цилиндрический сосуд, заполненный идеальным газом, разделен поршнем, который может двигаться без трения. В равновесии поршень находится посредине цилиндра. При малых смещениях из положения равновесия поршень совершает колебания. Найти зависимость частоты этих колебаний от температуры, считая процесс изотермическим.
Решение:
В положении равновесия давление $p$ на поршень слева и справа одинаково. Поскольку объем газа слева и справа одинаков, а температура $T$ постоянна, из уравнения Менделеева — Клапейрона
$pV = nu RT$ (1)
следует, что количество газа $nu$ одинаково по обе стороны от поршня. Отметим, что химический состав газов может быть различным.

рис.1
Пусть поршень сместился из положения равновесия, например влево, на малую величину $x$, так что $Sx ll V$, где $S$ — площадь поршня (рис. 1). Поскольку температура по условию не меняется, то
$(p + Delta p_{1})(V – Sx) = (p – Delta p_{2}) (V + Sx)$.
Раскрыв скобки и приведя подобные члены, получим
$( Delta p_{1} + Delta p_{2}) V – ( Delta p_{1} – Delta p_{2}) Sx = 2pSx$.
Второе слагаемое слева много меньше первого не только потому, что $Sx ll V$, но и вследствие того, что множителем при $V$ стоит сумма двух близких величин $Delta p_{1}$ и $Delta p_{2}$, а множителем при $Sx$ — их разность. Пренебрегая вторым слагаемым, получаем
$Delta p_{1} + Delta p_{2} = frac{2pS}{V} x$.
Результирующая сила, действующая на поршень, равна
$F = – frac{2pS^{2}}{V} x$.
Знак минус означает, что сила направлена в сторону, противоположную направлению смещения поршня, т. е. к положению равновесия. Под действием силы, пропорциональной смещению, поршень массой $M$ будет совершать гармонические колебания с частотой $omega$, определяемой соотношением
$omega^{2} = 2pS^{2}/VM$. (2)
При решении задачи мы молчаливо предполагали, что масса газа много меньше массы поршня, так что кинетической энергией макроскопического движения газа при колебаниях поршня можно пренебречь но сравнению с кинетической энергией поршня. Подумайте, где использовано это условие.
Выразив $p$ из уравнения Менделеева — Клапейрона (1), получим
$omega^{2} = frac{2 nu RS^{2}}{MV^{2}} T$. (3)
Таким образом, частота колебаний поршня пропорциональна $sqrt{T}$, ибо коэффициент при $T$ в формуле (3) не зависит от температуры, если пренебречь тепловым расширением сосуда.
Подумайте теперь, какие условия должны выполняться, чтобы процесс действительно был изотермическим. Для того чтобы температура газа в процессе колебаний не изменялась, необходим хороший тепловой контакт с большим тепловым резервуаром — термостатом, имеющим постоянную температуру. Что значит хороший тепловой контакт? Это значит, что время установления термодинамического равновесия между газом в сосуде и термостатом должно быть много меньше периода колебаний поршня. Тогда можно считать, что газ в каждый момент имеет ту же температуру, что и термостат. Если, наоборот, период колебаний окажется много меньше времени установления термодинамического равновесия между газом и термостатом, то можно считать, что колебания поршня происходят практически без обмена теплотой с термостатом. В этом случае процесс можно считать адиабатическим, несмотря на отсутствие тепловой изоляции сосуда с поршнем. Оказывается, что зависимость частоты колебаний от температуры при этом будет такой же, как и в изотермическом случае, только коэффициент в формуле (3) умножится на число, большее единицы. Увеличение частоты колебаний при адиабатическом процессе можно объяснить, сравнивая $p-V$ – диаграммы изотермического и адиабатического процессов идеального газа.
Отметим, что приведенное решение в обоих случаях имеет смысл, только если время установления теплового равновесия в самом газе много меньше периода колебаний поршня, так как в противном случае вообще теряют смысл такие равновесные макроскопические характеристики газа, как давление и температура. Другими словами, по отношению к самому газу процесс должен быть квазистатическим.
Источник
Сжатие газа поршнем, движущимся в глухой трубе с постоянной скоростью
Вариантом описанной в параграфе 9.5.1 задачи является задача о сжатии газа поршнем, движущимся с постоянной скоростью от входа в трубу в направлении глухого торца. В этом случае процесс сжатия газа должен происходить посредством формирования перед движущимся поршнем волны сжатия или ударной волны, и последующего распространения ее перед поршнем и отражения от глухого конца, затем от поршня и т.д. Подобный вариант рассчитывался в ППП «МАТМЕХ». Результатом расчетов сжатия газа глухой трубе длиной 1,18 м поршнем движущимся со скоростью 100 м/с в течение 0,011 с представлены на рис. 9.28 и 9.29. Продольная сетка включала 40 узлов. Изменение массы газа в замкнутом объеме между поршнем и торцом трубы за время расчета не превышало 1,5 %, что свидетельствует о достаточной точности вычислений. На рис. 9.28 изображено распределение плотности в сечении ? = 0 (линия с треугольниками) и ?, = 1 (сплошная линия). На рис. 9.29 представлено распределение давления по длине канала во времени на неподвижной оси. Результаты иллюстрируют волновой про-

Рис. 9.28. Распределение плотности в сечении Е, = 0 (линия с треугольниками)
и ? = 1 (сплошная линия)

Рис. 9.29. Изменение давления газа в канале со временем
цесс сжатия газа поршнем в глухой трубе и позволяют сделать вывод о работоспособности расчетного метода применительно к расчету течений газов на подвижных сетках, адаптирующихся к положению ограничивающих поток подвижных элементов.
Сжатие газа в глухой трубе поршнем пиропривода
Рассматривается случай, соответствующий варианту, описанному в подпараграфе 9.5.1 при отсутствии жидкости в канале ГЖВС. Поршень сосуда С2 сжимает воздух, находящийся в канале К1, правый торец которого неподвижный и глухой. Объем сосуда С2 в начальный момент соответствует удалению поршня от левого торца цилиндра ГЖВС на 0,05 м. В сосуде воспламеняется и сгорает заряд пороха ДРПЗ массой 50 г. Масса поршня составляет 4 кг. Поршень удерживается элементами форсирования, разрушающимися при давлении 11 ата в сосуде С2. Разгоняемый давлением пороховых газов поршень сжимает воздух в глухом цилиндре слева от поршня. В результате должен произойти удар поршня о глухой торец, амортизируемый газовой прослойкой между поршнем и глухим торцом. В конечном итоге должен реализоваться периодический колебательный процесс движения поршня в трубе. Толщина прослойки воздуха между поршнем и глухим торцом при сжатии стремится к нулю, что делает задачу весьма жесткой и осложняет вычислительный процесс. При стремлении к нулю длины канала К1 шаг по времени, выбираемый из условия Куранта для канала, будет весьма малым. При резком изменении параметров в сосуде С2 в период вспышки пороха или в период сжатия газа в сосуде должен уменьшаться шаг интегрирования уравнений изменения параметров в сосуде, выбираемый по значениям контрольного члена и заданной относительной погрешности. Разработанный в рамках ППП «МАТМЕХ» программный комплекс позволяет успешно решить поставленную задачу, сочетая выбор шага по времени по контрольному члену второго порядка с использованием условия Куанта. Результаты расчетов на сетке, включающей 40 узлов по длине канала представлены на рис. 9.30—9.33. Длина канала К1 составляла 0,1 м, что соответствовало толщине газовой прослойки в ГЖВС, рассмотренной ниже. В отличие от предыдущего случая движение поршня начинается из неподвижного состояния и максимальная скорость поршня составляет около 72 м/с, то есть является существенно дозвуковой. Шаг интегрирования меняется пропорционально текущей длине канала К1 и в момент отражения поршня достигает величины порядка 0,3 • 10-9 с. Дозвуковое движение поршня обусловливает выполнение в канале обычного для классической баллистики допущения о линейном распределении скорости газа между движущимся поршнем и глухим торцом. Кривые изменения скорости по длине канала в зависимости от безразмерной координаты ?, е [0, 1] представлены на рис. 9.30, соответствующие кривые для давления — на рис. 9.31. На

Puc. 9.30. Изменение скорости газа в канале
в течение первой четверти периода колебаний

Puc. 9.31. Изменение давления газа в канале в течение первой четверти периода колебаний

Рис. 9.32. Изменение параметров течения в канале в сечении ? = 0,0

Рис. 9.33. Изменение параметров течения в канале в сечении ?=1,0
рис. 9.32 и 9.33 приведены кривые измерения параметров потока на движущемся поршне (2, = 0) и на глухом торце (?, = 1). Расчетная картина соответствует физике процесса. Рассчитан период времени, соответствующий двум периодам колебаний поршня в трубе. Проведенный расчет позволяет сделать вывод о физически правильном представлении взаимодействия поршня с газом в сосуде С2 и канале К1 в разработанном алгоритме.
Источник
Задача по физике – 1495
Цикл, совершаемый некоторой массой идеального одноатомпого газа, состоит из двух изохор и двух изобар. Известно, что наибольшее давление в два раза больше наименьшего, а наибольший объем в четыре раза больше наименьшего в данном процессе. Найти КПД цикла.

Подробнее
Задача по физике – 1496
Поршень массы $M$, замыкающий объем $V_{0}$ идеального одноатомного газа при давлении $P_{0}$ и температуре $T_{0}$, движется со скоростью $v$. Определить температуру газа при максимальном сжатии. Теплообменом пренебречь.
Подробнее
Задача по физике – 1497
В горизонтальном неподвижном цилиндрическом сосуде, закрытом поршнем массы М, находится моль идеального одноатомного газа. Газ нагревают. Поршень, двигаясь равноускоренно, приобретает скорость v. Сколько тепла подведено газу? Теплоемкостью сосуда и поршня, а также внешним давлением пренебречь.
Подробнее
Задача по физике – 1498
Моль газа участвует в циклическом процессе, график которого состоит из двух изохор и двух изобар (см. рис.) Температуры газа в точках 1 и 3 равны соответственно $T_{1}$ и $T_{3}$. Определить работу, совершенную газом за цикл, если известно, что точки 2 и 4 лежат на одной изотерме.

Подробнее
Задача по физике – 1499
Найти теплоемкость системы, состоящей из перекрытого поршнем сосуда с одноатомным газом (параметры $P_{0}, V_{0}, T_{0}$). Поршень удерживается пружиной. Слева от поршня вакуум. Если газ откачать, поршень соприкоснется с правой стенкой сосуда, а пружина будет недеформирована. Теплоемкостями сосуда, поршня и пружины пренебречь.
Подробнее
Задача по физике – 1500
Из небольшого отверстия в баллоне со сжатым гелием вытекает струя газа со скоростью $v$. Найти разность температур гелия в баллоне и в струе. Давление в струе считать равным внешнему давлению, скоростью газа в баллоне при расчетах пренебречь.
Подробнее
Задача по физике – 1501
Какую работу надо совершить, чтобы каплю жидкости объемом $V$ с поверхностным натяжением $sigma$ растянуть в пленку, толщина которой $d$ мала по сравнению с первоначальным радиусом капли?
Подробнее
Задача по физике – 1502
Найти поверхностное натяжение жидкости, если петля из резиновой нити длины $l_{0}$ и жесткости $k$, положенная на пленку этой жидкости, растянулась до окружности радиуса $R$ после прокола пленки внутри петли.
Подробнее
Задача по физике – 1503
Железный кубик, смазанный парафином, плавает в воде так, что его верхняя грань находится на уровне воды. Вода не смачивает парафин. Найти длину ребра кубика.
Подробнее
Задача по физике – 1504
Определить толщину слоя жидкости, разлитой па горизонтальной плоскости. Краевой угол $theta$, плотность жидкости $rho$, поверхностное натяжение $sigma$.
Подробнее
Задача по физике – 1505
Вычислить давление жидкости под ее сферической поверхностью радиуса $R$, вызванного силами поверхностного натяжения. Коэффициент $sigma$ известен.
Подробнее
Задача по физике – 1506
Вычислить давление внутри мыльного пузыря радиуса $R$. Коэффициент поверхностного натяжения $sigma$, внешнее давление отсутствует.
Подробнее
Задача по физике – 1507
Найти радиус кривизны капли в ее верхней точке А. Масса капли $M$, ее высота $H$, радиус соприкосновения капли с горизонтальной плоскостью, на которой она находится, равен $r$. Плотность жидкости $rho$, поверхностное натяжение $sigma$. Плоскость не смачивается жидкостью.
Подробнее
Задача по физике – 1508
Капля ртути массы $m = 1 г$ помещена между двумя параллельными стеклянными пластинками. Какую силу надо приложить к верхней пластинке, чтобы ртуть имела форму круглой лепешки радиуса $R = 5 см$? Поверхностное натяжение ртути $sigma = 0,465 frac{Н}{м}$. Ртуть не смачивает стекло.
Подробнее
Задача по физике – 1509
В вакууме в чашку с маслом, имеющим весьма низкую упругость пара и полностью смачивающим стекло, погружена стеклянная капиллярная трубка радиуса $r$. Найти давление в масле на высоте $frac{H}{3}$ над уровнем масла в чашке, где $H$ — высота, на которую поднимется масло в капилляре. Поверхностное натяжение масла равно $sigma$.
Подробнее
Источник