При увеличении температуры давление газа на стенки сосуда
Давление газа — что это за параметр
Определение
Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.
Определение
Газ — это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.
В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.
Примечание
По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.
Причина возникновения давления в газах
Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.
Примечание
Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична.
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.
Свойства давления газа:
- Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
- Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
- В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.

Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:
(P=frac{F}{S})
Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
(F*Δt = Δp)
Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.
Формула давления идеального газа из молекулярно-кинетической теории
Объяснение концепции идеального газа построено на основных положениях молекулярно-кинетической теории, которая вытекает из принципов статистической механики. Наука получила активное развитие во второй половине XIX, благодаря таким ученым, как Джеймс Максвелл и Людвиг Больцман. Основы дисциплины были заложены еще Бернулли в первой половине XVIII века.

Исходя из статистики Максвелла-Больцмана, все частицы в системе обладают разными скоростями движения. При этом можно наблюдать небольшой процент частиц со скоростями, приближенными к нулю, и малую долю частиц, обладающих огромной скоростью. Средняя квадратичная скорость в этом случае будет соответствовать некоторой величине, не изменяющейся с течением времени.
Средняя квадратичная скорость частиц однозначно характеризует температуру газа. Используя приближения молекулярно-кинетической теории в виде невзаимодействующих безразмерных и хаотично движущихся частиц, получают формулу для расчета давления газа в сосуде:
(P=frac{N*m*v^{2}}{3*V})
где N является количеством частиц в системе; V обозначает объем; v представляет собой среднюю квадратичную скорость; m является массой одной частицы.
При наличии указанных в формуле параметров, выраженных в единицах СИ, можно вычислить давление газа в сосуде.
Второй способ записи основного уравнения МКТ
Определение
В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:
(P*V = n*R*T )
n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.
Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.
Определение
С помощью данного выражения можно определить формулу для расчета давления газа:
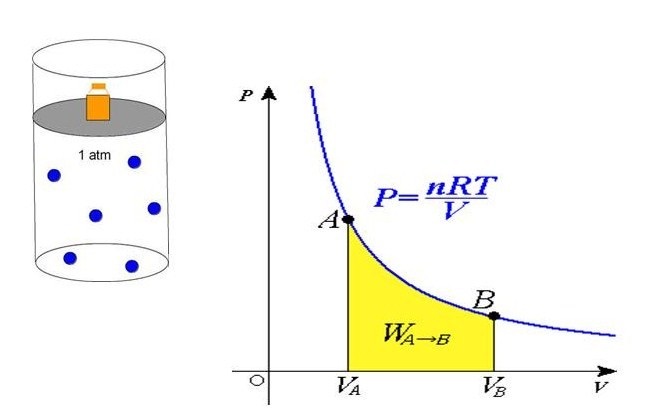
(P=frac{n*R*T}{V})
Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.

Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.

Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m. В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:
- Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
- Применение закона Дальтона, согласно которому давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример
Предположим, что молекулы кислорода движутся со средней скоростью в 500 м/с. Требуется рассчитать, каково давление в сосуде, объем которого равен 10 литров, содержащий 2 моль молекул.
Для того чтобы найти ответ, следует применить формулу для Р из молекулярно-кинетической теории:
(P=frac{N*m*v^{2}}{3*V})
Из-за неизвестных параметров m и N требуется выполнить некоторые преобразования формулы:
(m=frac{M}{NA})
(n=frac{N}{NA})
(m*N= M*n)
(P=frac{M*n*v^{2}}{3*V})
Таким образом, удельный объем сосуда в кубических метрах равен 0,01. Молярная масса молекулы кислорода М составляет 0,032 кг/моль. Данные параметры можно подставить в уравнение вместе со скоростью и количеством вещества. Тогда Р = 533333 Па, что представляет собой давление в 5,3 атмосферы.
Источник
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:
• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;
• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).
Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.
Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.
Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .
Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.
Изотермический процесс
Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.
Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:
Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.
Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:
(1)
Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:
(2)
Данное утверждение называется законом Бойля — Мариотта.
Записав закон Бойля — Мариотта в виде
(3)
можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.
Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.
Графики изотермического процесса
Вообще, графики термодинамических процессов принято изображать в следующих системах координат:
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат .
График изотермического процесса называется изотермой.
Изотерма на -диаграмме — это график обратно пропорциональной зависимости .
Такой график является гиперболой (вспомните алгебру — график функции ). Изотерма-гипербола изображена на рис. 1.

Рис. 1. Изотерма на -диаграмме
Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на –диаграмме.
В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2). Первый процесс идёт при температуре , второй — при температуре .

Рис. 2. Чем выше температура, тем выше изотерма
Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление , на второй — . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, .
В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3):

Рис. 3. Изотермы на и -диаграммах
Изобарный процесс
Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.
Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно
где — атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .
Выпишем уравнения состояния:
Поделив их друг на друга, получим:
В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
(4)
А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:
(5)
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:
(6)
Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.
Графики изобарного процесса
График изобарного процесса называется изобарой. На -диаграмме изобара является прямой линией (рис. 4):

Рис. 4. Изобара на -диаграмме
Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.
Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на –диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и (рис. 5):

Рис. 5. Чем ниже изобара, тем больше давление
Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).
Стало быть, .
В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6):

Рис. 6. Изобары на и -диаграммах
Изохорный процесс
Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и . Имеем:
Делим эти уравнения друг на друга:
Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
(7)
Ввиду произвольности выбора состояний мы приходим к закону Шарля:
(8)
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:
(9)
Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.
Графики изохорного процесса
График изохорного процесса называется изохорой. На -диаграмме изохора является прямой линией (рис. 7):

Рис. 7. Изохора на -диаграмме
Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.
Далее, чем больше объём, тем ниже идёт изохора на –диаграмме (рис. 8):

Рис. 8. Чем ниже изохора, тем больше объём
Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, .
В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9):

Рис. 9. Изохоры на и -диаграммах
Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.
Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
Источник
Глава 3. Давление твёрдых тел, жидкостей и газов
Мы уже знаем, что газы, в отличие от твёрдых тел и жидкостей, заполняют весь сосуд, в котором они находятся. Например, стальной баллон для хранения газов, камера автомобильной шины или волейбольный мяч. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твёрдого тела на опору.
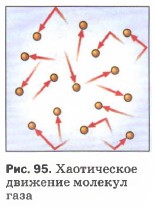
Известно, что молекулы газа беспорядочно движутся. При своём движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ (рис. 95). Молекул в газе много, потому и число их ударов очень велико. Например, число ударов молекул воздуха, находящегося в комнате, о поверхность площадью 1 см2 за 1 с выражается двадцатитрёхзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул на стенки сосуда значительно, оно и создаёт давление газа.
Итак, давление газа на стенки сосуда (и на помещённое в газ тело) вызывается ударами молекул газа.

Рассмотрим следующий опыт. Под колокол воздушного насоса помещают завязанный резиновый шарик. Он содержит небольшое количество воздуха (рис. 96, а) и имеет неправильную форму. Затем насосом откачивают воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится всё более разреженным, постепенно раздувается и принимает форму шара (рис. 96, б).
Как объяснить этот опыт?
В нашем опыте движущиеся молекулы газа непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул в колоколе вокруг оболочки шарика уменьшается. Но внутри завязанного шарика их число не изменяется. Поэтому число ударов молекул о внешние стенки оболочки становится меньше, чем число ударов о внутренние стенки. Шарик раздувается до тех пор, пока сила упругости его резиновой оболочки не станет равной силе давления газа. Оболочка шарика принимает форму шара. Это показывает, что газ давит на её стенки по всем направлениям одинаково. Иначе говоря, число ударов молекул, приходящихся на каждый квадратный сантиметр площади поверхности, по всем направлениям одинаково. Одинаковое давление по всем направлениям характерно для газа и является следствием беспорядочного движения огромного числа молекул.

Попытаемся уменьшить объём газа, но так, чтобы масса его осталась неизменной. Это значит, что в каждом кубическом сантиметре газа молекул станет больше, плотность газа увеличится. Тогда число ударов молекул о стенки сосуда возрастёт, т. е. возрастёт давление газа. Это можно подтвердить опытом.
На рисунке 97, а изображена стеклянная трубка, один конец которой закрыт тонкой резиновой плёнкой. В трубку вставлен поршень. При вдвигании поршня объём воздуха в трубке уменьшается, т. е. газ сжимается (рис. 97, б). Резиновая плёнка при этом выгибается наружу, указывая на то, что давление воздуха в трубке увеличилось.
Наоборот, при увеличении объёма этой же массы газа число молекул в каждом кубическом сантиметре уменьшится. От этого уменьшится число ударов о стенки сосуда — давление газа станет меньше. Действительно, при вытягивании поршня из трубки объём воздуха увеличивается, плёнка прогибается внутрь сосуда (рис. 97, в). Это указывает на уменьшение давления воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в трубке находился любой другой газ.
Итак, при уменьшении объёма газа его давление увеличивается, а при увеличении объёма давление уменьшается при условии, что масса и температура газа остаются неизменными.

А как изменится давление газа, если нагреть его при постоянном объёме? Известно, что скорость движения молекул газа при нагревании увеличивается. Двигаясь быстрее, молекулы будут ударять о стенки сосуда чаще. Кроме того, каждый удар молекулы о стенку сосуда станет сильнее. Вследствие этого стенки сосуда будут испытывать большее давление.
Следовательно, давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объём не изменяются.
Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.
Для хранения и перевозки газов их сильно сжимают. При этом давление их возрастает, газы приходится заключать в специальные, очень прочные стальные баллоны (рис. 98). В таких баллонах, например, содержат сжатый воздух в подводных лодках, кислород, используемый при сварке металлов.
Вопросы
1. Какие свойства газов отличают их от твёрдых тел и жидкостей?
2. Как объясняют давление газа на основе учения о движении молекул?
3. Как можно на опыте показать, что газ производит давление на стенки сосуда, в котором он находится?
4. Из чего можно заключить, что газ производит одинаковое давление по всем направлениям?
5. Почему давление газа увеличивается при сжатии и уменьшается при расширении?
6. Почему сжатые газы содержат в специальных баллонах?
Задание
Надуйте воздушный шарик и крепко его завяжите. Положите в любую ёмкость. Вначале облейте его водой, охлаждённой в морозильной камере (до 5°С), затем горячей водой (70°С). Дайте объяснение наблюдаемому явлению.
Источник
