Пример расчета давления жидкости на дно и стенки сосуда

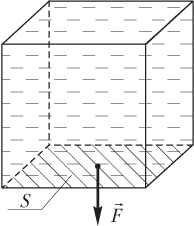
Рассмотрим, как можно рассчитать давление жидкости на дно и стенки сосуда. Решим сначала задачу с числовыми данными. Прямоугольный бак наполнен водой (рис. 96). Площадь дна бака 16 м2, высота его 5 м. Определим давление воды на дно бака.
Сила, с которой вода давит на дно сосуда, равна весу столба воды высотой 5 м и площадью основания 16 м2, иначе говоря, эта сила равна весу всей воды в баке.

Чтобы найти вес воды, надо знать ее массу. Массу воды можно вычислить по объему и плотности. Найдем объем воды в баке, умножив площадь дна бака на его высоту: V= 16 м2*5 м=80 м3. Теперь определим массу воды, для этого умножим ее плотность p = 1000 кг/м3 на объем: m = 1000 кг/м3 * 80 м3 = 80 000 кг. Мы знаем, что для определения веса тела надо его массу умножить на 9,8 Н/кг, так как тело массой 1 кг весит 9,8 Н.
Следовательно, вес воды в баке равен P = 9,8 Н/кг * 80 000 кг ≈ 800 000 Н. С такой силой вода давит на дно бака.
Разделив вес воды на площадь дна бака, найдем давление p:
p = 800000 H/16 м2 = 50 000 Па = 50 кПа.
Давление жидкости на дно сосуда можно рассчитать, пользуясь формулой, что значительно проще. Чтобы вывести эту формулу, вернемся к задаче, но только решим ее в общем виде.
Обозначим высоту столба жидкости в сосуде буквой h, а площадь дна сосуда S.
Объем столба жидкости V= Sh.
Масса жидкости т = pV,или m = pSh.
Вес этой жидкости P = gm, или P = gpSh.
Так как вес столба жидкости равен силе, с которой жидкость давит на дно сосуда, то, разделив вес P на площадь S, получим давление р:
p = P/S, или p = gpSh/S
т. е.
p = gph.
Мы получили формулу для расчета давления жидкости на дно сосуда. Из этой формулы видно, что давление жидкости на дно сосуда прямо пропорционально плотности и высоте столба жидкости.
По этой формуле можно вычислять и давление на стенки, сосуда, а также давление внутри жидкости, в том числе давление снизу вверх, так как давление на одной и той же глубине одинаково по всем направлениям.
При расчете давления по формуле:
p = gph
надо плотность p выражать в килограммах на кубический метр (кг/м3), а высоту столба жидкости h — в метрах (м), g = 9,8 Н/кг, тогда давление будет выражено в, паскалях (Па).
Пример. Определить давление нефти на дно цистерны, если высота столба нефти 10 м, а плотность ее 800 кг/м3.

Вопросы. 1. От каких величин зависит давление жидкости на дно сосуда? 2. Как зависит давление жидкости на дно сосуда от высоты столба жидкости? 3. Как зависит давление жидкости на дно сосуда от плотности жидкости? 4. Какие величины надо знать, чтобы рассчитать давление жидкости на стенки сосуда? 5. По какой формуле рассчитывают давление жидкости на дно и стенки сосуда?
Упражнения. 1. Определите давление на глубине 0,6 м в воде, керосине, ртути. 2. Вычислите давление воды на дно одной из глубочайших морских впадин, глубина, которой 10 900 м, Плотность морской воды 1030 кг/м3. 3. На рисунке 97 изображена футбольная камера, соединенная с вертикально расположенной стеклянной трубкой. В камере и трубке находится вода. На камеру положена дощечка, а на нее — гиря массой 5 кг. Высота столба воды в трубке 1 м. Определите площадь соприкосновения дощечки с камерой.

Задания. 1. Возьмите высокий сосуд. В боковой поверхности его по прямой, на разной высоте от дна сделайте три небольших отверстия. Закройте отверстия спичками и налейте в сосуд до верха воды. Откройте отверстия и проследите за струйками вытекающей воды (рис. 98). Ответьте на вопросы: почему вода вытекает из отверстий? Из чего следует, что давление увеличивается с глубиной? 2. Прочтите в конце учебника параграфы «Гидростатический парадокс. Опыт Паскаля», «Давление на дне морей и океанов. Исследование морских глубин».
Источник
Что это такое?
В сосуде, заполненном водой, на дно давит сила, равная весу столба жидкости. Это вызванное силой тяжести давление называется гидростатическим.
Оно определяется отношением силы к площади, то есть его физический смысл – это сила, действующая на единицу площади (см2).
 Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Вставив в бочку, заполненную водой, длинную узкую трубку, он налил в нее несколько кружек воды, и бочку разорвало.
Согласно закону Паскаля, приложенное к H2O усилие распространяется равномерно во всем объеме. Это объясняется тем, что вода почти не сжимается. В гидравлических прессах используют это свойство.
Плотность воды все же растет при высоком давлении. Это учитывается при расчетах конструкций глубоководных аппаратов.
Факторы, влияющие на показатель
При отсутствии внешнего воздействия, играют роль два фактора:
- высота столба;
- плотность.
Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.
Сверху на содержимое сосуда давит также атмосферный воздух. Поэтому в сообщающихся сосудах уровень одинаков, ведь в каждом из них над поверхностью атмосфера одна и та же.
Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:
- внешней силы;
- веса воды.
При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.

На дно и стенку сосуда – в чем разница?
Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.
Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.
Наполнив сосуд, имеющий отверстия одного диаметра в стенках на разной высоте, можно наблюдать различный напор вытекающей струи. Чем выше отверстие – тем слабее струя. То есть, давление на стенки емкости тем больше, чем ближе ко дну.
Единицы измерения
 Давление воды измеряют в:
Давление воды измеряют в:
- паскалях – Па;
- метрах водяного столба – м. в. ст.
- атмосферах – атм.
Практически достаточно знать, что 1 атмосфера равна 10 метрам водяного столба или 100000 Па (100кПа).
Формулы расчета
Давление на дно сосуда рассчитывается делением силы на площадь, то есть оно равно произведению плотности воды, высоты столба и ускорения свободного падения g (величина постоянная, равна 9,8 м/с2).
Пример расчета: бак наполнен водой (плотность 1000 кг/м3) до высоты 1,2 м. Нужно найти, какое давление испытывает дно бака. Решение: P = 1000*1, 2*9, 8 = 11760 Па, или 11, 76 кПа.
Для расчета давления на стенки сосуда применяют все ту же формулу напора, приведенную выше. При расчете берется глубина от точки, в которой нужно рассчитать напор, до поверхности воды.
Пример расчета: на глубине 5 м на стенку резервуара с водой будет оказываться давление P=1000 *5 * 9, 8=49000 кПа, что составляет 0,5 атмосферы.
Расчет давления воды на дно и стенки сосуда в видео:
Применение на практике
Примеры использования знаний свойств воды:
-
 Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм.
Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм. - Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
- Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
- Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.
Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:
- выжимка масла из семян растений;
- спуск на воду со стапелей построенного судна;
- ковка и штамповка деталей;
- домкраты для подъема грузов.
Заключение
Такие свойства воды, как текучесть и несжимаемость, дают возможность использовать силу ее давления для самых различных целей.
Опасность этого явления учитывают при расчетах на прочность корпусов подводных лодок, стенок и днищ резервуаров, в которых хранят воду. Сила давления воды совершает полезную работу, она же способна и разрушать.
А какова Ваша оценка данной статье?
Источник
Æèäêîñòè (è ãàçû) ïåðåäàþò ïî âñåì íàïðàâëåíèÿì íå òîëüêî âíåøíåå äàâëåíèå, íî è òî äàâëåíèå, êîòîðîå ñóùåñòâóåò âíóòðè íèõ áëàãîäàðÿ âåñó ñîáñòâåííûõ ÷àñòåé.
Äàâëåíèå, îêàçûâàåìîå ïîêîÿùåéñÿ æèäêîñòüþ, íàçûâàåòñÿ ãèäðîñòàòè÷åñêèì.
Ïîëó÷èì ôîðìóëó äëÿ ðàñ÷åòà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè íà ïðîèçâîëüíîé ãëóáèíå h (â îêðåñòíîñòè òî÷êè A íà ðèñóíêå).

Ñèëà äàâëåíèÿ, äåéñòâóþùàÿ ñî ñòîðîíû âûøåëåæàùåãî óçêîãî ñòîëáà æèäêîñòè, ìîæåò áûòü âûðàæåíà äâóìÿ ñïîñîáàìè:
1) êàê ïðîèçâåäåíèå äàâëåíèÿ p â îñíîâàíèè ýòîãî ñòîëáà íà ïëîùàäü åãî ñå÷åíèÿ S:
2) êàê âåñ òîãî æå ñòîëáà æèäêîñòè, ò. å. ïðîèçâåäåíèå ìàññû m æèäêîñòè íà óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ:
F=mg. (1.28)
Ìàññà æèäêîñòè ìîæåò áûòü âûðàæåíà ÷åðåç åå ïëîòíîñòü p è îáúåì V:
m = pV, (1.29)
à îáúåì — ÷åðåç âûñîòó ñòîëáà è ïëîùàäü åãî ïîïåðå÷íîãî ñå÷åíèÿ:
V=Sh. (1.30)
Ïîäñòàâëÿÿ â ôîðìóëó (1.28) çíà÷åíèå ìàññû èç (1.29) è îáúåìà èç (1.30), ïîëó÷èì:
F = pVg=pShg. (1.31)
Ïðèðàâíèâàÿ âûðàæåíèÿ (1.27) è (1.31) äëÿ ñèëû äàâëåíèÿ, ïîëó÷èì:
pS = pSkg.
Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî ðàâåíñòâà íà ïëîùàäü S, íàéäåì äàâëåíèå æèäêîñòè íà ãëóáèíå h:
p = phg.
Ýòî è åñòü ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.
Ãèäðîñòàòè÷åñêîå äàâëåíèå íà ëþáîé ãëóáèíå âíóòðè æèäêîñòè íå çàâèñèò îò ôîðìû ñîñóäà, â êîòîðîì íàõîäèòñÿ æèäêîñòü, è ðàâíî ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè, óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ è ãëóáèíû, íà êîòîðîé îïðåäåëÿåòñÿ äàâëåíèå.
Âàæíî åùå ðàç ïîä÷åðêíóòü, ÷òî ïî ôîðìóëå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ìîæíî ðàññ÷èòûâàòü äàâëåíèå æèäêîñòè, íàëèòîé â ñîñóä ëþáîé ôîðìû, â òîì ÷èñëå, äàâëåíèå íà ñòåíêè ñîñóäà, à òàêæå äàâëåíèå â ëþáîé òî÷êå æèäêîñòè, íàïðàâëåííîå ñíèçó ââåðõ, ïîñêîëüêó äàâëåíèå íà îäíîé è òîé æå ãëóáèíå îäèíàêîâî ïî âñåì íàïðàâëåíèÿì.
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ .
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ — ÿâëåíèå, çàêëþ÷àþùååñÿ â òîì, ÷òî âåñ æèäêîñòè, íàëèòîé â ñîñóä, ìîæåò îòëè÷àòüñÿ îò ñèëû äàâëåíèÿ æèäêîñòè íà äíî ñîñóäà.
 äàííîì ñëó÷àå ïîä ñëîâîì «ïàðàäîêñ» ïîíèìàþò íåîæèäàííîå ÿâëåíèå, íå ñîîòâåòñòâóþùåå îáû÷íûì ïðåäñòàâëåíèÿì.
Òàê, â ðàñøèðÿþùèõñÿ êâåðõó ñîñóäàõ ñèëà äàâëåíèÿ íà äíî ìåíüøå âåñà æèäêîñòè, à â ñóæàþùèõñÿ — áîëüøå.  öèëèíäðè÷åñêîì ñîñóäå îáå ñèëû îäèíàêîâû. Åñëè îäíà è òà æå æèäêîñòü íàëèòà äî îäíîé è òîé æå âûñîòû â ñîñóäû ðàçíîé ôîðìû, íî ñ îäèíàêîâîé ïëîùàäüþ äíà, òî, íåñìîòðÿ íà ðàçíûé âåñ íàëèòîé æèäêîñòè, ñèëà äàâëåíèÿ íà äíî îäèíàêîâà äëÿ âñåõ ñîñóäîâ è ðàâíà âåñó æèäêîñòè â öèëèíäðè÷åñêîì ñîñóäå.

Ýòî ñëåäóåò èç òîãî, ÷òî äàâëåíèå ïîêîÿùåéñÿ æèäêîñòè çàâèñèò òîëüêî îò ãëóáèíû ïîä ñâîáîäíîé ïîâåðõíîñòüþ è îò ïëîòíîñòè æèäêîñòè: p = pgh (ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè). À òàê êàê ïëîùàäü äíà ó âñåõ ñîñóäîâ îäèíàêîâà, òî è ñèëà, ñ êîòîðîé æèäêîñòü äàâèò íà äíî ýòèõ ñîñóäîâ, îäíà è òà æå. Îíà ðàâíà âåñó âåðòèêàëüíîãî ñòîëáà ABCD æèäêîñòè: P = oghS, çäåñü S — ïëîùàäü äíà (õîòÿ ìàññà, à ñëåäîâàòåëüíî, è âåñ â ýòèõ ñîñóäàõ ðàçëè÷íû).
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ îáúÿñíÿåòñÿ çàêîíîì Ïàñêàëÿ — ñïîñîáíîñòüþ æèäêîñòè ïåðåäàâàòü äàâëåíèå îäèíàêîâî âî âñåõ íàïðàâëåíèÿõ.
Èç ôîðìóëû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñëåäóåò, ÷òî îäíî è òî æå êîëè÷åñòâî âîäû, íàõîäÿñü â ðàçíûõ ñîñóäàõ, ìîæåò îêàçûâàòü ðàçíîå äàâëåíèå íà äíî. Ïîñêîëüêó ýòî äàâëåíèå çàâèñèò îò âûñîòû ñòîëáà æèäêîñòè, òî â óçêèõ ñîñóäàõ îíî áóäåò áîëüøå, ÷åì â øèðîêèõ. Áëàãîäàðÿ ýòîìó äàæå íåáîëüøèì êîëè÷åñòâîì âîäû ìîæíî ñîçäàâàòü î÷åíü áîëüøîå äàâëåíèå.  1648 ã. ýòî î÷åíü óáåäèòåëüíî ïðîäåìîíñòðèðîâàë Á. Ïàñêàëü. Îí âñòàâèë â çàêðûòóþ áî÷êó, íàïîëíåííóþ âîäîé, óçêóþ òðóáêó è, ïîäíÿâøèñü íà áàëêîí âòîðîãî ýòàæà, âûëèë â ýòó òðóáêó êðóæêó âîäû. Èç-çà ìàëîé òîëùèíû òðóáêè âîäà â íåé ïîäíÿëàñü äî áîëüøîé âûñîòû, è äàâëåíèå â áî÷êå óâåëè÷èëîñü íàñòîëüêî, ÷òî êðåïëåíèÿ áî÷êè íå âûäåðæàëè, è îíà òðåñíóëà.

Источник
4.2. Элементы гидростатики
4.2.3. Гидростатическое давление
Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление.
Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле
pгидр = ρ0gh,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости.
В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).
Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:
Fгидр = pгидрS = ρ0ghS,
где pгидр — гидростатическое давление на дно сосуда; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь дна сосуда.
Рис. 4.10
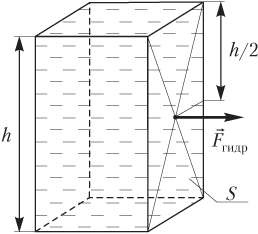
Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле
pгидр=ρ0gh2,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота вертикальной стенки сосуда (столба жидкости).
Рис. 4.11
Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:
Fгидр=pгидрS=ρ0gh2S,
где pгидр — гидростатическое давление на дно сосуда; ρж — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь вертикальной стенки.
Рис. 4.11
При расчете давленияна днооткрытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — глубина водоема.
Рис. 4.12
Сила давления на дно открытого водоема определяется произведением:
F = pS = (pатм + ρ0gh)S,
где S — площадь дна водоема.
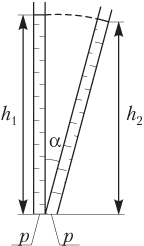
Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:
p = ρ0gh1 cos α,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h1 — высота столба жидкости при вертикальном положении мензурки; h2 = h1 cos α — высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.
Рис. 4.13
Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см3. Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.
Решение. Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:
〈Fгидр〉=〈p〉S,
где 〈p〉 — среднее гидростатическое давление на боковую поверхность цилиндра; S — площадь боковой поверхности цилиндра.
Найдем каждый из сомножителей следующим образом:
- среднее гидростатическое давление на боковую поверхность цилиндра
〈p〉=ρ0gh2,
где ρ0 — плотность жидкости, заполняющей сосуд; g — модуль ускорения свободного падения; h — высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;
- площадь боковой поверхности цилиндра
S = 2πRh,
где 2πr — длина окружности; R — радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямоугольника, одна из сторон которого равна высоте цилиндра, а другая — периметру круга (длине окружности), лежащего в его основании.
Подстановка среднего гидростатического давления 〈p〉 и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:
〈Fгидр〉=πρ0gRh2.
Расчет дает значение:
〈Fгидр〉=π⋅2,5⋅103⋅10⋅10⋅10−2⋅(30⋅10−2)2≈707 Н≈0,71 кН.
Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см3. Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.
Решение. Давление в открытом водоеме определяется формулой
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность воды; g — модуль ускорения свободного падения; h — искомая глубина водоема.
По условию задачи
p = 4pатм.
Подстановка указанного значения в исходную формулу дает:
4pатм = pатм + ρ0gh,
или
3pатм = ρ0gh.
Выразим отсюда искомую глубину водоема
h=3pатмρ0g
и произведем вычисление:
h=3⋅100⋅1031,0⋅103⋅10=30 м.
Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.
Источник
«Кто смолоду больше делает и думает сам, тот становится потом надежнее, крепче, умнее». С. Нерис
Цели урока:
- Образовательные:
- активизировать знания учащихся о причинах возникновения давления жидкости,
- создать условия для овладения учащимися формулы для расчета давления жидкости на дно и стенки сосуда,
- продолжить работу по формированию навыков научного познания мира,
- создать условия для овладения учащимися эвристическим методом представления наблюдаемого явления – методом графических образов.
- Развивающие:
- развивать экспериментальные умения, навыки логического мышления, умение обосновывать свои высказывания, делать выводы, выделять главное, представлять информацию в различных знаковых системах,
- развивать у учащихся интерес к познанию законов природы и их применению;
- развивать умение проводить рефлексию своей деятельности.
- Воспитательные:
- создать условия для приобретения убежденности учащихся в познаваемости окружающего мира,
- приучать учащихся к доброжелательному общению, взаимопомощи, к самооценке.
Задачи урока:
- изучение теоретического материала;
- решение задач на расчет давления в жидкости и газе;
- практическое значение знаний о давлении жидкости.
План урока:
- Организационный момент. (1 мин.)
- Актуализация знаний. (5 мин.)
- Объяснение материала. (20 мин.)
- Закрепление материала. (15 мин.)
- Рефлексия. (2 мин.)
- Домашнее задание. (2 мин.)
Ход урока
I. Организационный момент.
(На партах учащихся лежат рабочие карты урока, в которых представлены две самостоятельные работы и критерии выставления оценки; две ручки с разными стержнями, например синий и зеленый; таблицы плотностей веществ, учебники и тетради).
II. Актуализация знаний.
Самостоятельная работа (см. рабочую карту)
III. Объяснение нового материала
Провожу эксперимент: в пластмассовую бутылку с тремя отверстиями на разных уровнях по высоте наливаем подкрашенную воду.
Беседа с классом:
- почему вода вытекает из сосуда?
- сравните струи воды?
- объясните, почему они разные?
Когда учащиеся объяснят, что столбы жидкости разные и давление на разной глубине разное, ставлю проблему: а нужно ли знать людям, чему равно давление жидкости на разных глубинах, на дно, на стенки сосуда?
Открываем тетради, записываем тему урока.
Ставим цель: вывести формулу для расчета давления жидкости на дно и стенки сосуда.
Давление жидкости (см. презентация)
Вокруг нас много жидкостей. Одни из них движутся, например, вода в реках или нефть в трубах, другие – покоятся. При этом все они имеют вес и поэтому давят на дно и стенки сосуда, в котором находятся. Подсчет давления движущейся жидкости – непростая задача, поэтому изучим лишь как рассчитывать давление, создаваемое весом покоящейся жидкости. Оно называется гидростатическим давлением и вычисляется по следующей формуле.
| p – давление слоя жидкости, Па |
| ρ – плотность жидкости, кг/м3 |
| g – коэффициент, Н/кг |
| h – высота слоя жидкости, м |
Рассмотрим, как выведена эта формула. Сила F, с которой жидкость давит на дно сосуда, является весом жидкости. Его мы можем подсчитать по формуле F тяж = mg, так как жидкость и ее опора (дно сосуда) покоятся. Вспомним также формулу m = ρV для выражения массы тела через плотность его вещества и формулу V = Sh для подсчета объема тела, имеющего форму прямоугольного параллелепипеда. В результате имеем равенство:
Это равенство иллюстрирует не только способ вывода формулы для вычисления гидростатического давления. Оно также показывает, что формула p = ρgh является частным случаем определения давления – формулы p = F/S.
Заметим также, что при выводе формулы совсем необязательно предполагать, что слой высотой h и плотностью ρ образован именно жидкостью. В наших рассуждениях ничего не изменится, если вместо давления жидкости мы рассмотрим давление твердого тела прямоугольной формы или даже газа, заключенного в соответствующий сосуд. Создаваемое ими весовое давление будет именно таким, как предсказывает формула p = ρgh.
Формула p = ρgh показывает, что давление, создаваемое слоем жидкости, не зависит от ее массы, а зависит от плотности жидкости, высоты ее слоя и места наблюдения. При увеличении толщины слоя жидкости или ее плотности гидростатическое давление будет возрастать.
Полученный нами вывод можно проверить опытами. Проделаем их. Справа изображена стеклянная трубка с водой, дно которой затянуто тонкой резиновой пленкой. Увеличивая высоту слоя налитой жидкости, мы будем наблюдать увеличение растяжения пленки. Этот опыт подтверждает, что при увеличении высоты слоя жидкости создаваемое ею давление увеличивается.
На следующем рисунке изображены трубки с водой и “крепким” раствором соли. Видно, что уровни жидкостей находятся на одной и той же высоте, но давление на пленку в правой трубке больше. Это объясняется тем, что плотность раствора соли больше, чем плотность обычной воды.
На доске нарисован параллелепипед высотой h и площадью основания S. Предлагаю ребятам представить, что это аквариум, в котором налита вода. Попытаемся определять давление воды Р на дно аквариума. Работаем на магнитной доске с карточками, выкладывая поочередно формулы, получая цепочку: m=ρV, V=Sh, m=ρSh, P=gm, P=gρSh, ρ=P/S, p=ρgh.
Анализируем окончательную формулу: что же нужно знать, чтобы рассчитать давление жидкости.
Зависит ли давление от площади или формы сосуда?
Вьполняем фронтальный эксперимент: на каждой парте стоит стакан с водой. Высота налитой воды одинаковая.
Цель: определить давление воды на дно стакана.
Один ученик выполняет у доски. Остальные за партой. Сверяем ответ. Анализируем его: какую физическую величину мы измеряли? какую физическую величину брали в таблице? какое численное значение давления получили учащиеся, работающие за партой и у доски? большое это или маленькое давление?
IV. Закрепление изученного материала.
- ~ Приведи примеры движущихся жидкостей.
- И движущиеся, и покоящиеся жидкости оказывают давление …
- Гидростатическое давление – это …
- ~ Произведение в правой части формулы для вычисления гидростатического давления представляет собой …
- ~ По какой формуле мы сможем подсчитать вес покоящейся жидкости?
- Объем слоя жидкости мы нашли при помощи произведения …
- Выражение “p = … = ρgh” представляет собой …
- ~ О чем говорит равенство p=ρgh?
- Как можно подтвердить справедливость формулы p=ρgh?
- ~ Увеличение растяжения пленки свидетельствует, что …
- Описанный опыт иллюстрирует зависимость гидростатического давления от ..
- ~ Плотность раствора соли больше, чем плотность воды. Это приводит к тому, что …
- Этот опыт иллюстрирует зависимость давления жидкости от ее плотности. Эта иллюстрация стала возможной благодаря тому, что …
Расчетные задачи
а) Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, если бы она была налита вместо воды?
б) Какое давление на дно сосуда оказывает слой керосина высотой 1,5 м?
Качественные задачи
в) Волк плывет под водой с дыхательной трубкой. Какие ограничения накладывает на ныряльщика дыхательная трубка? Ответ найдите в учебнике стр. 95.
Задача с недостающими данными
г) Какое давление на глубине 1,5 м? Решить устно.
Качественные задачи, предполагающие работу с дополнительными источниками информации
д) Какое преимущество дает ныряльщику акваланг? Какие ограничения он накладывает? Ответ в учебнике.
е) В следующем сюжете мы видим глубоководный аппарат. Почему у него такая внешняя форма?
ж) Чтобы человек мог работать на больших глубинах он должен находиться в специальном скафандре. Найдите о нем информацию в учебнике.
з) Анализируя рис. 103 учебника давайте познакомимся с тем, что говорит нам учебник о глубоководных аппаратах. Какие ограничения в их использовании имеются?
и) Вычислите, какое давление в самой глубокой Мариинской впадине глубиной.
к) В просмотренном сюжете мы видели с вами глубоководных рыб. Какую длину лески нужно приготовить для лова рыбы камбалы, если она может выдерживать давление 400 кПа.
V. Задаю домашнее задание:
параграф из учебника, упражнение на решение задач и сообщения:
- «Человек изучает подводный мир».
- «Подводные лодки, батисферы и батискафы».
- «Животный мир океанских и морских глубин».
- «Ныряльщики за жемчугом».
Источник