Прямолинейное равноускоренное движение сосуда с жидкостью

Если при движении сосуда на частицы жидкости, кроме сил тяжести действуют еще силы инерции, под действием этих сил жидкость принимает новое положение равновесия – положение относительного покоя.
Относительным покоем называется равновесие жидкости, находящейся под действием сил тяжести и инерции в движущемся сосуде.
При относительном покое положение свободной поверхности и поверхностей уровня, отличается от их положения для жидкости в неподвижном сосуде.
При определении формы и положения этих поверхности учитывается основное свойство поверхности уровня.
Основное свойство поверхностей уровня – равнодействующая массовых сил всегда нормальна к этим поверхностям.
В полном дифференциале давления
dP=ρ(X*dх+У*dy+Z*dz), (4.12)
Х,У,Z- алгебраическая сумма проекций на оси координат ускорений силы тяжести и сил инерции переносного движения.
Вдоль поверхности уровня dР=0, так как поверхности уровня – это поверхности равного давления. Дифференциальное уравнение поверхности равного давления:
X*dх+У*dy+Z*dz= 0 (4.13),
Этот трехчлен (4.13) определяет элементарную работу массовых сил X,У,Zна перемещенияхdх, dy, dz. В данном случае перемещение взято по поверхности равного давления,dР=0.
Из этого выражения следует, что работа массовых сил вдоль поверхности равного давления равна нулю. Это значит, что в состоянии относительного покоя результирующее ускорение перпендикулярно к соответствующему элементу поверхности равного давления.
Рассмотрим два случая относительного покоя.
Первый случай: сосуд, движущийся прямолинейно и равноускоренно.
Второй случай: сосуд, вращающийся вокруг вертикальной оси с постоянной угловой скоростью.
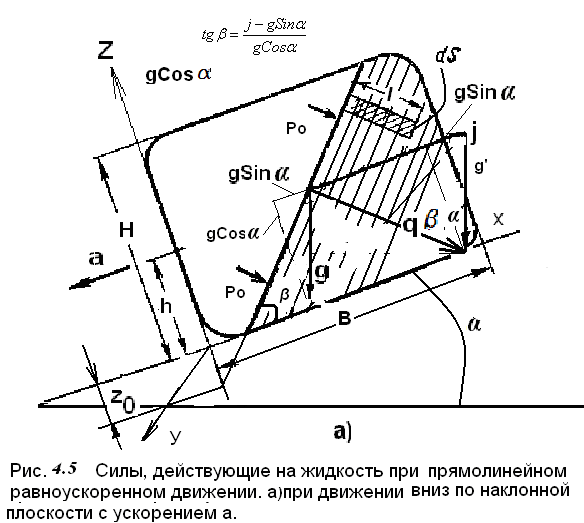
На рис.4.5 изображен сосуд, движущийся вниз с ускорением апо плоскости наклонённой под угломα к горизонту. Оси координат оси координат связаны с движущимся телом.
1. Пусть на жидкость действует суммарная массовая сила F, проекции которойFx,Fy,Fz, поделенные на массу:Fx/mявляются проекциями единичной массовой силы на оси Ох, Оу, Oz: Х, У иZ.
F =Fx+Fy+Fz=mа,F/m=Fx/m+Fy/m+Fz/m=X+Y+Z=а.
Все выделенные составляющие являются векторными величинами.
Проекции массовых сил, действующие на выделенный объем в направлении координатных осей, будут равны произведениям проекций единичных сил, умноженным на массу выделенного объема.
Fx = mX, Fy = mY, Fz = mZ.
Результирующую единичнуюмассовую силу, действующую на жидкость, найдем как сумму единичных векторов силы инерцииjи силы тяжестиg.Единичная сила инерцииFи = j =- aнаправлена в сторону противоположную ускорениюа(рис.4.5).
Проекции сумм массовых сил на оси:
Ox: X= j – gSinα,
Oz : Z= -gCosα,
Оx: Y= 0.
При подстановке этих проекций в дифференциал давления, получим
(1/ρ)dp= [(j – gSinα)dx- (gCosα)dz].
Проинтегрировав дифференциал в проекциях, получим выражение для давления на поверхностях уровня
Р = ρ [(j- gSinα) x- (gCosα)z] + С. (4.14)
На произвольной поверхности уровня давление постоянно Р = constи, обозначив новую постоянную С1- Р = const,где Р получим уравнение изобарических поверхностей
ρ [(j – gSina) x- ρgCosa* z] +С1 = 0(4.15)
Это уравнение дает семейство плоскостей, параллельных оси Оу. Одной из них является свободная поверхность.
Обозначим через z0координату пересечения свободной поверхности с осьюz.Подставив в формулу (4.15)х0 = 0, z= z0, находимС1=ρgz0Cosαдля свободной поверхности. Уравнение этой поверхности имеет вид
ρ [(j – gSina) x- ρgCosa* z] + ρg z0Cosα= 0
(j – gSina) x -gCosa*( z + z0) = 0

где коэффициент в линейном уравнении равен тангенсу угла β .
Для определения положения свободной поверхности жидкости в сосуде, движущемся прямолинейно и равноускоренно к уравнению (4.16) нужно добавить уравнение объемов, т. е. нужно знать первоначальный объем жидкости в сосуде и выразить его через размеры сосуда В и Н и первоначальный уровень h.
Если сосуд движется только под действием силы тяжести, то j= gSinα β= 0, то свободная поверхность параллельна плоскости движения.
При нулевых условиях: х = 0,z= z0,P = P0в формуле (4.14), получимC=P0+ (ρgCosa)z0:
Р = ρ [(j- gSinα) x- (gCosα)z+ С
Р = P0+ρ(j-gSina)x+ρgCosa(z0- z). (4.19)
Эта формула используется для определения давления в любой точке жидкости, находящейся в относительном покое при прямолинейном движении
Можно также использовать суммарную массовую единичную силу qдля определения давления в любой точке.
Возьмем на рис.4.5 около точки М площадку dS, параллельную свободной поверхности, и на этой площадке построим цилиндрический объем с осью, нормальной к свободной поверхности. Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид
РdS = P0dS+ q(ρldS),
где последний член представляет собой полную массовую силу, q- суммарная единичная массовая сила, М = ρldS- масса выделенного объема жидкости,l – расстояние от точки М до свободной поверхности.
После сокращения на dSполучим давление в точке
Р = P0+ qρl, (4.20)
Соседние файлы в папке Лекции и семинары
- #
- #
- #
Источник
Содержание:
- Прямолинейное равноускоренное движение сосуда с жидкостью
Прямолинейное равноускоренное движение сосуда с жидкостью
Прямолинейное равноускоренное движение сосуда с жидкостью. Ранее рассматривалось равновесие жидкостей под действием преимущественно 1-й массовой силы (ее веса).Этот случай имеет место, когда жидкость неподвижна относительно Земли и неподвижна в равномерно и прямолинейно движущемся сосуде. Если емкость с жидкостью имеет неравномерное или нелинейное движение, то, помимо силы тяжести, на частицы жидкости также действует сила инерции, и если время постоянно, то жидкость занимает новое равновесное положение. Равновесие этой жидкости называется относительным покоем.
При относительной неподвижности свободная поверхность жидкости и другие горизонтальные поверхности могут существенно отличаться от горизонтальной поверхности, когда жидкость неподвижна в неподвижном контейнере, то есть когда она неподвижна с горизонтальной поверхности. Людмила Фирмаль
- При определении формы и расположения свободной поверхности жидкости в относительном стационарном состоянии необходимо руководствоваться основными характеристиками любой горизонтальной поверхности, а именно: фактически, если результирующая массовая сила действует под определенным углом относительно горизонтальной плоскости, то тангенциальная составляющая этой силы заставляет частицу двигаться 2 $ Жидкость по поверхности уровня. Но в относительном спокойном состоянии нет движения частиц жидкости относительно стенки сосуда или относительно каждого из них other. As в результате, единственно возможное направление равноденствия Л * * и Действующая массовая сила перпендикулярна поверхности свободной поверхности и другим уровням.
Разные ценности, это невозможно. Рассмотрим 2 характерных случая относительного покоя жидкости: сосуд, который ускоряется и движется линейно и равномерно, и сосуд, который вращается вокруг вертикальной оси с постоянной угловой скоростью. Перемещайте емкость с жидкостью по прямой линии с постоянной accelerationa. In в этом случае мы находим результирующую массовую силу, действующую на жидкость, как сумму 1 в. 1 + Индуцированная инерция Ускорение а и сила тяжести на другую сторону(рис. 1.17).Показать вектор связанных синтетических массовых сил К единичной массе получим, где А и% единичный вектор силы инерции и силы тяжести.
- Для всех частиц рассматриваемого объема жидкости силы результирующей массы параллельны друг другу, а горизонтальная плоскость перпендикулярна им forces. So, все горизонтальные плоскости, включая свободные, являются плоскостями, параллельными друг другу. Угол наклона этих плоскостей относительно горизонта определяется из условия перпендикулярности к силе / плоскости Чтобы определить положение свободной поверхности жидкости в линейно равномерно ускоренном и движущемся сосуде, уравнение объема должно быть добавлено к предыдущим условиям. То есть необходимо знать объем жидкости в сосуде и выражать его размерами сосудов B и H и начальным уровнем жидкости K.
Уравнение, позволяющее найти давление в любой точке рассматриваемого объема жидкости, может быть получено таким же образом, как и 1,5 члена. Например, Точка M (13y параллельна свободной поверхности, а точки На этой плоскости свободный&Д1 & свободный построить цилиндрический том с шинопроводом перпендикулярным к поверхности. Условие равновесия для указанного объема жидкости в направлении, перпендикулярном свободной поверхности, является: П <18 = ■ РО&8+] Р1 38、 Где последний член-суммарная массовая сила, действующая на объем выбранной жидкости, I-расстояние от точки L /до свободной поверхности. После получать и уменьшения П-по + / п ^ *(1.33).
Поверхность уровня не может пересекать друг друга. Если нет, то вдоль двух пересекающихся линий такой поверхности получается ряд точек, и одновременно возникает два давления. Людмила Фирмаль
- В некоторых случаях a равно 0, и поэтому/является уравнением (1.33), которое является основным гидростатическим уравнением(1-20). Если вы интегрируете дифференциальное уравнение (1.24), то получите то же самое уравнение(1.33).Для этого удобнее ориентировать одну из координатных осей вдоль линии действия результирующей массовой силы 7. 1.Например, если вы берете это направление относительно оси 2 *、 X-Y-0; BПоэтому вместо уравнения (1.24) можно написать Зр=р/ 31. Или после консолидации и определения путем постоянной замены параметров свободной поверхности р = р] 1 + п. Полученное уравнение соответствует уравнению (1.33).
Смотрите также:
Методические указания по гидравлике
Возможно эти страницы вам будут полезны:
- Сила давления жидкости на плоскую стенку.
- Сила давления жидкости на криволинейные стенки. Плавание тел.
- Равномерное вращение сосуда с жидкостью.
- Кинематика и динамика жидкости
Источник
В этом случае на частицы жидкости кроме силы тяжести действуют еще и силы инерции, при этом жидкость принимает новое положение равновесия – относительный покой.
Свободная поверхность жидкости отличается по углу наклона от горизонтальной плоскости.
Основное свойство поверхности уровня: равнодействующая массовых сил всегда нормальна к поверхности уровня. Если бы она действовала под другим углом, то возникающие касательные напряжения перемещали бы поверхность уровня жидкости в другое положение.
a
a
J
a- ускорение сосуда j=a+g- сумма единичных векторов сил инерции и веса.
Для определения положения свободной поверхности жидкости в сосуде, движущимся прямолинейно, необходимо решить уравнение объемов.
Давление в произвольной точке M 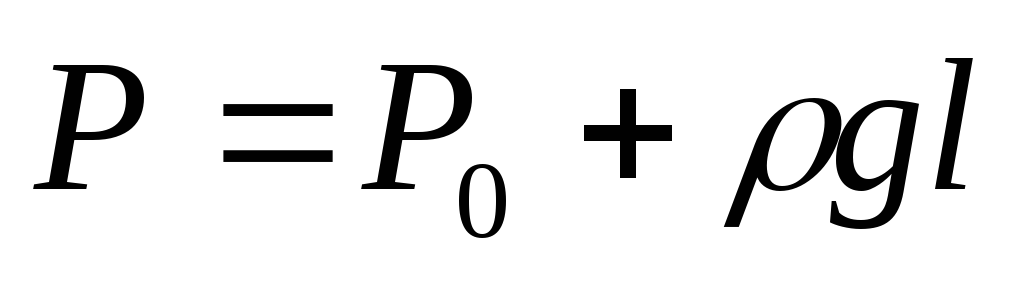 ,гдеl – расстояние по нормали от свободной поверхности до точки M.
,гдеl – расстояние по нормали от свободной поверхности до точки M.
Равномерное вращение сосуда с жидкостью
Раскрутим цилиндрический сосуд с жидкостью до постоянной скорости и будем ее поддерживать
A P0 B
r 2r
g j
Массовая сила состоит:
сила тяжести – g
центробежная сила – 2r
Равнодействующая массовая сила – jувеличивается с радиуса за счет ее центробежной составляющей, а угол ее наклона к горизонту уменьшается. Наклон поверхности с увеличением радиуса возрастает.
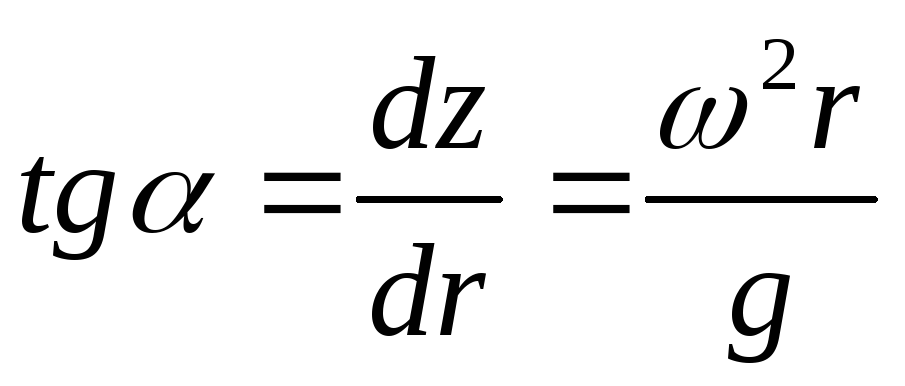 ;
;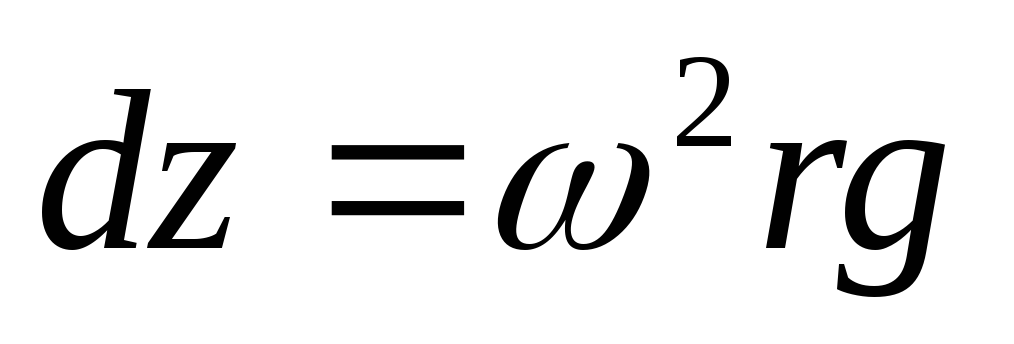 ;
;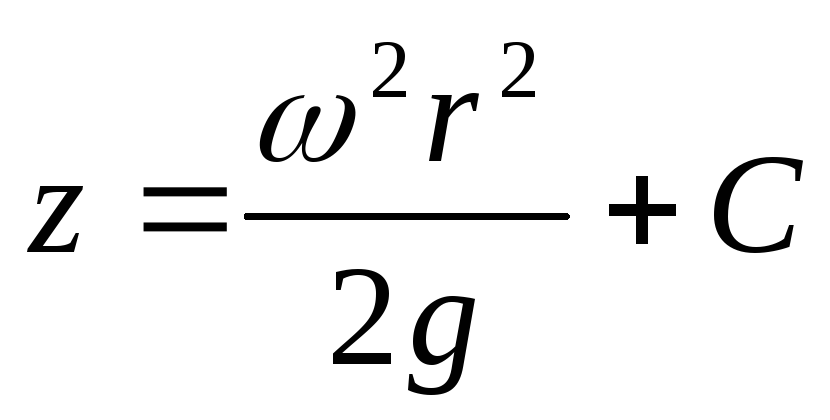
В точке пересечения кривой AOB c осью вращения r=0, z=h=c, и окончательно: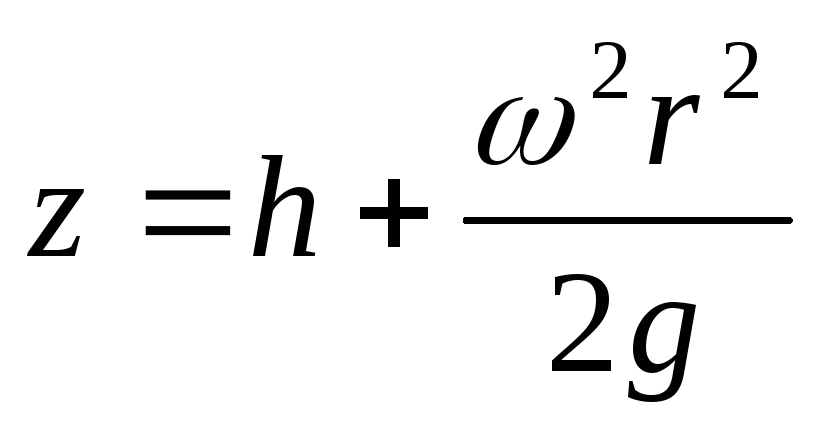 – уравнение параболы. Давление выражается формулой:
– уравнение параболы. Давление выражается формулой:
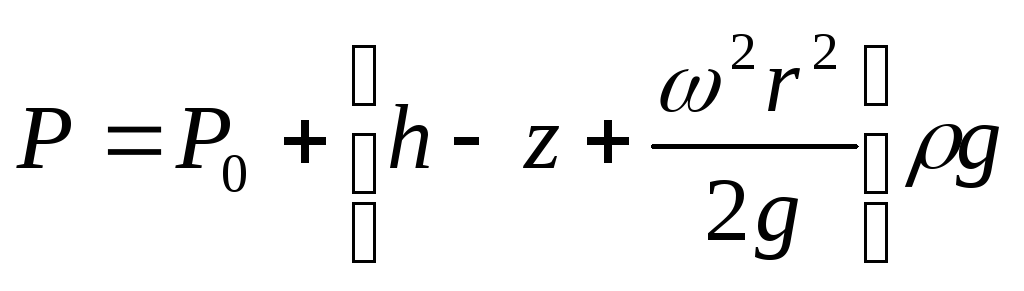
Кинематика и динамика жидкости
1.Основные понятия и определения.
Скорость каждой точки пространства, занятого движущейся жидкостью, является функцией координат точки и времени. Задача кинематики – нахождение поля скоростей.
В идеальной (невязкой) жидкости возможен лишь один вид напряжений – нормальные напряжения сжатия, т.е. давление.
Течение жидкости может быть установившимся и неустановившимся. Установившееся движение характеризуется неизменностью параметров во времени.
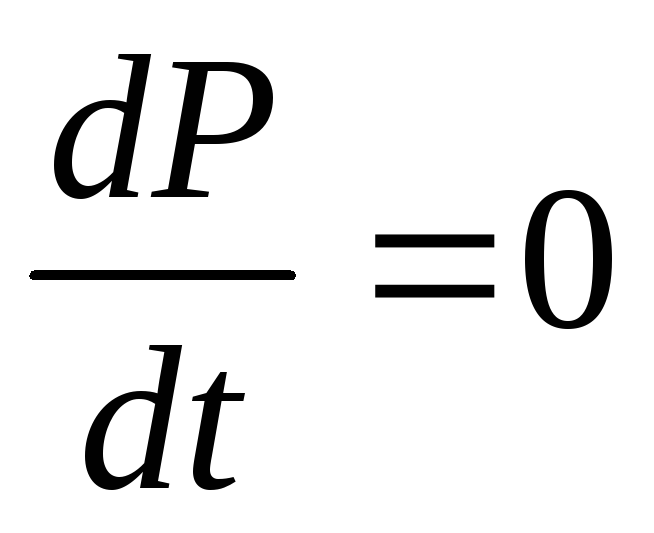 ;
;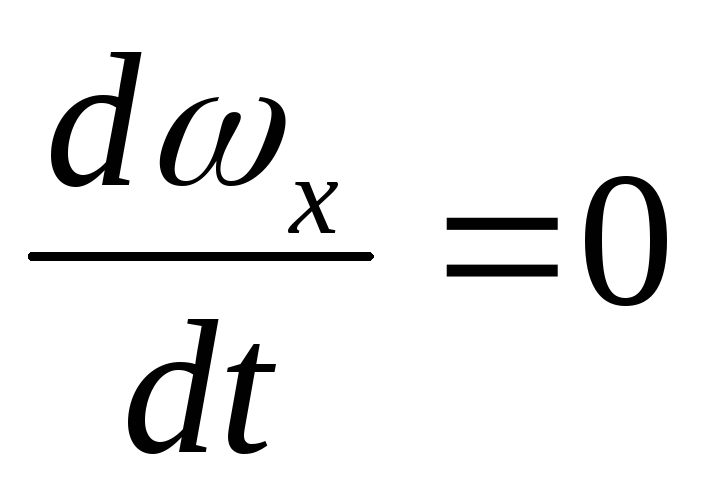 ;
;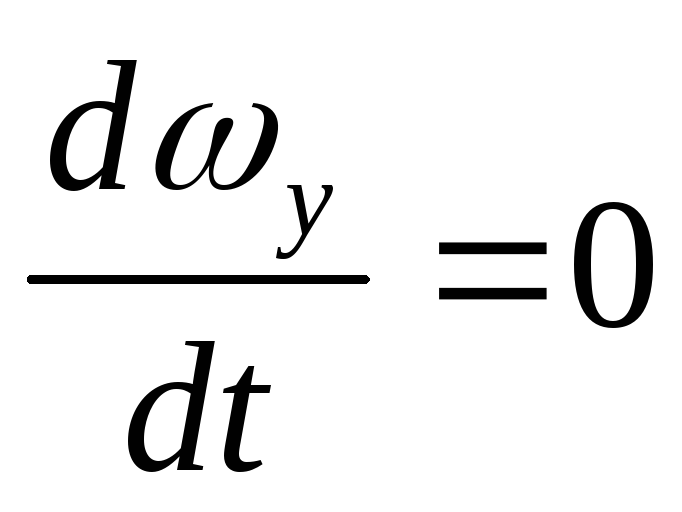 ;
;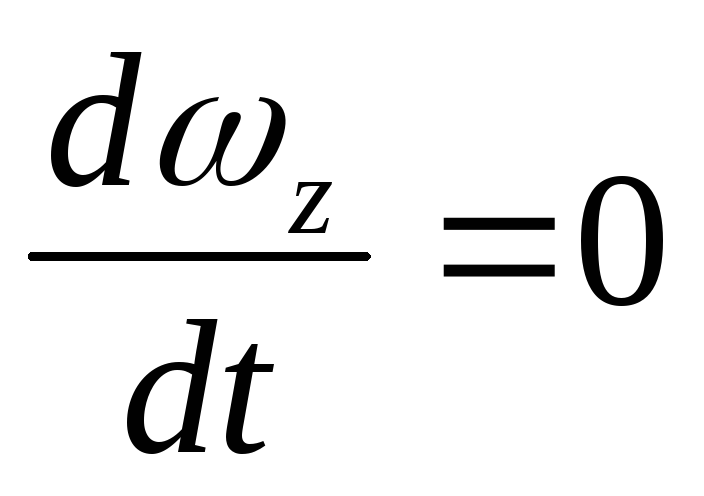
Равномерное движение характеризуется неизменностью параметров вдоль потока.
Параметры неустановившегося движения жидкости меняются как по координатам, так и по времени.
ПРИМЕРЫ – опорожнение сосуда через отверстие в его дне или движение в напорной трубе поршневого насоса.
Траектории частиц жидкости при установившемся движении постоянны.
Линия тока – кривая, в каждой точке которой вектор скорости в любой момент времени направлен по касательной.
1
3
2
При установившемся движении жидкости линия тока совпадает с траекторией.
Трубка тока – совокупность линий тока, проведенных через малый замкнутый контур в движущейся жидкости.
Элементарная струйка – часть потока, заключенная внутри трубки тока.
При установившемся движении трубка тока является непроницаемой, т.е. частицы жидкости через нее не протекают.
Поток конечных растворов состоит из элементарных струек не перемешивающихся между собой.
Живое сечение – поверхность внутри потока, проведенная нормально к линии тока. В случае параллельных струек живое сечение плоское.
Соседние файлы в папке Gidrogazovaya_dinamika
- #
- #
Источник
Относительное равновесие жидкости. Равновесие жидкости под действием сил тяжести и инерции
Когда жидкость покоится в неподвижном относительно Земли сосуде или в сосуде, движущемся равномерно и прямолинейно, на нее действует только одна массовая сила – ее собственный вес. Этот случай равновесия жидкости называется абсолютным покоем.
Если же сосуд с жидкостью находится в неравномерном или непрямолинейном дви- жении, то на все частицы жидкости, помимо собственного веса, действуют еще силы инер- ции переносного движения. Под действием этих сил жидкость как-то перемещается в сосуде, и если эти силы постоянны во времени, то жидкость принимает новое положение равновесия, т. е. становится неподвижной относительно стенок сосуда. Этот случай равновесия жидкости называется относительным покоем.
При относительном покое свободная поверхность жидкости и другие поверхности уровня могут существенно отличаться от поверхности уровня при покое жидкости в непод- вижном сосуде, т. е. от горизонтальной поверхности. Для определения формы и положения свободной поверхности жидкости в относительном покое руководствуются основным свой- ством всякой поверхности уровня, которое заключается в том, что равнодействующая массо- вая сила всегда действует нормально к поверхности уровня.
Выбирая систему координат, жестко связанную со стенками сосуда, приходим к стати- ческой задаче, основой для решения которой служит дифференциальное уравнение равнове- сия жидкости:
dp = ρ(X dx + Y dy + Z dz), (3.1)
где x, y, z – координаты точек жидкости в системе отсчета, связанной с сосудом;
p – давление в жидкости;
ρ – плотность жидкости;
X, Y, Z – проекции единичной массовой силы на координатные оси.
Для определения формы поверхности уровня и характера распределения давления в этом сосуде следует в число действующих массовых сил включить также силы инерции.
Существуют два состояния относительного покоя жидкости:
– в сосуде, движущемся прямолинейно и равноускоренно;
– в сосуде, равномерно вращающемся вокруг вертикальной оси.
Прямолинейное равноускоренное движение сосуда с жидкостью
Сосуд с жидкостью движется с ускорением a вдоль прямой, наклоненной к горизонту под углом a (рис. 3.1).
К массовым силам j = – a, наряду с силой тяжести в данном случае относится еще и сила инерции, направленная проти- воположно ускорению сосуда. В системе координат (рис. 3.1) проекции единичных массовых сил будут равны
X = j – g´sin a ;
Y = 0 ;
Z = – g´cos a.
Подставляя эти выражения в урав- нение равновесия (3.1), получаем
dp = r [(j – g´sin a)dx – g´cos a dz],
а после интегрирования
p = r (j – g´sin a)´x – r g´cos a´z + C,
Рис. 3.1. Относительное равновесие жидкости при
прямолинейном равноускоренном движении сосуда
(3.2)
где С – постоянная интегрирования, определяемая из граничных условий на свободной по- верхности при x = 0, z = z0 и p = p0.
После подстановки граничных условий получаем закон распределения давления:
p = р0+ r (j – g´sin a)´x + r ´g´cos a´(z0- z). (3.3) Так как на поверхности уровня давление одинаково в любой ее точке, полагая в урав-
нении (3.2) p = const, получаем уравнение поверхностей уровня
r ( j – g´sin a)´x – r ´g´cos a´z + C1 = 0. (3.4) Уравнение (3.4) дает семейство плоскостей, параллельных оси Y. Одной из этих плос-
костей является свободная поверхность.
Подставляя в формулу (3.4) граничные условия x = 0 и z = z0, находим
C1= r ´g´z0´cos a.
Уравнение свободной поверхности имеет вид
j – g sin a
где
j – g sin a =tgq.
g cos a
z – z0 =
g cos a
x , (3.5)
Источник
Если сосуд с жидкостью неравномерно движется, то на жидкость действуют силы веса и инерционные силы. Под их действием частицы жидкости принимают новое положение. Если движение равноускоренное, то новое положение оказывается равновесным, и жидкость находится в относительном покое. Свободная поверхность и поверхности уровня не горизонтальные. Форма этих поверхностей определяется величиной и направлением равнодействующей массовых сил. При этом равнодействующая всегда перпендикулярна поверхности (первое свойство гидростатического давления). Поверхности уровня не могут пересекаться, т.к. в этом случае в одной точке действовало бы два разных давления.
Р ассмотрим сосуд с жидкостью, движущийся с постоянным ускорением a.
Жидкость в этом сосуде займёт новое равновесное положение. Равновесие объёма жидкости описывается полным дифференциалом давления:
Определим давление в произвольной точке жидкости. Для этого возьмём произвольную точку M на расстоянии lот свободной поверхности. Кроме этого выберем систему координат, такую, что ось Z направлена по перпендикуляру к свободной поверхности. Такое расположение оси не изменит существа вывода, но математические выражения будут проще и более узнаваемы. Тогда при прямолинейном движении в выбранной системе координат:
Подставив эти значения в выражение для полного дифференциала, получим
После интегрирования будем иметь
Постоянную интегрирования C найдём из граничных условий на свободной поверхности, когда при , . Постоянная C примет вид . После подстановки получим в окончательном виде
.
Итоговая формула аналогична основному уравнению гидростатики, с той лишь разницей, что вместо глубины h используется расстояние от наклонной свободной поверхности l, а вместо ускорения свободного падения g – равнодействующее ускорение R.
Покой при равномерном вращении сосуда с жидкостью
Рассмотрим сосуд с жидкостью, вращающийся вокруг вертикальной оси с постоянной скоростью ω. На жидкость действуют внешнее давление, силы тяжести и инерционные силы. В результате их действия жидкость принимает новое равновесное положение. Свободная поверхность принимает форму параболоида. Рассмотрим на этой поверхности произвольную точку N. Равнодействующая сила R, действующая в т. N, перпендикулярна к свободной поверхности. Величина этой силы увеличивается с увеличением радиуса, а угол её наклона к горизонту уменьшается. Из этого следует, что наклон этой поверхности к горизонту увеличивается с ростом радиуса. Таким образом, сила R определяет форму свободной поверхности. Найдём математическую формулу этой кривой.
И з рисунка видно, что
Выразим отсюда dz :
Проинтегрировав, будем иметь:
.
Постоянную интегрирования найдём из известных условий: при . Подставив эти значения в последнее равенство, получим, что . В итоге будем иметь формулу, описывающую форму кривой, образующей свободную поверхность:
Теперь определим давление в жидкости, используя полный дифференциал давления
Для данного случая относительного покоя
С учётом этого полный дифференциал давления примет вид
Проинтегрируем эту функцию
Результатом интегрирования будет являться выражение
Учитывая, что , где r – радиус вращения, получим
Постоянную интегрирования C определим из условия, что при , тогда . Постоянная интегрирования с учётом принятых условий будет
Тогда формула, выражающая давление в жидкости, вращающейся с постоянной угловой скоростью, примет вид
Заметим, что в итоговом выражении первое слагаемое, характеризует давление внешней среды. Второе слагаемое описывает давление, созданное столбом жидкости, находящейся ниже точки 0, т.е. глубиной под уровнем нулевой точки. Третье слагаемое характеризуется высотой над точкой 0, и, следовательно, описывает давление, создаваемое жидкостью, поднимающейся по краям сосуда, причём эта величина зависит от расстояния точки от оси вращения. Таким образом, оказывается, что давление в каждой точке жидкости, вращающейся с постоянной скоростью относительно вертикальной оси, складывается из внешнего давления и давления столба жидкости над этой точкой.
Из приведённого анализа можно сделать следующий вывод. Сосуд с равномерно вращающейся жидкостью можно мысленно представить как совокупность сосудов, имеющих бесконечно малые площади. Давление в любой точке такого сосуда подчиняется основному уравнению гидростатики и подсчитывается привычным образом. Высота столба жидкости в сосудах зависит от частоты вращения и радиуса вращения реального сосуда. Отсюда становится понятно, что вариант равномерного вращения жидкости вокруг произвольно расположенной вертикальной оси (в начале лекции он отмечен цифрой 3) практически не отличается от уже рассмотренного.
Источник
