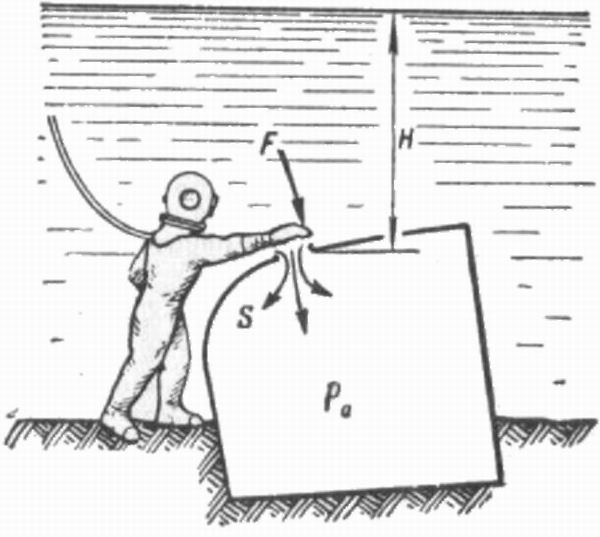
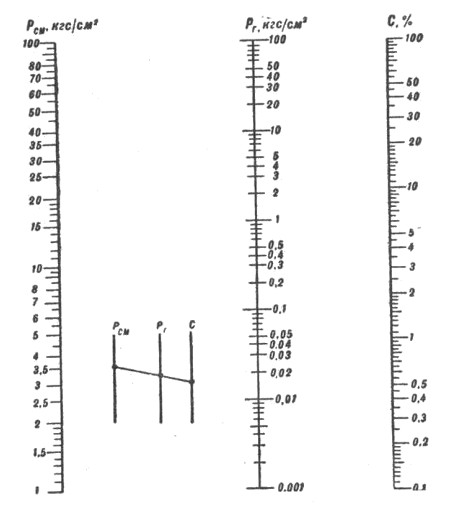
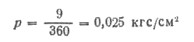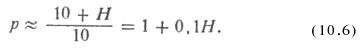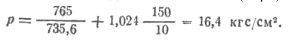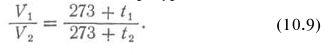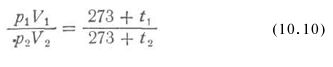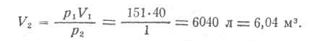Расчет давления воздуха в сосуде
Баннер Главный инструмент
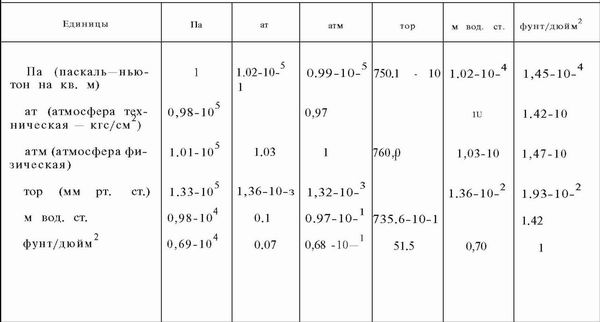
| Главная / Издания / Литература / Книжная полка / Справочник водолаза В водолазной практике часто приходится встречаться с В системах СИ и МКС единицей давления служит Механическое давление измеряется силой, действующей  где р — давление, кгс/см2; Пример 10.1. Определить давление, которое водолаз оказывает р = 180/360 = 0.5 кгс/см или в единицах СИ р = 0,5 * 0,98.105 = 49000 Па = 49 кПа. Таблица 10.1. | |||||||||
Источник
Любое вещество может быть описано своими физико-химическим параметрами. В отличие от жидких и твердых веществ, чье состояние может быть охарактеризовано температурой и плотностью, газы имеют еще один показатель, который называется «давление». Эта физическая величина для газообразного вещества может быть представлена итоговым значением сил ударов молекул о стенки сосуда, содержащего газ. Чем больше молекул ударяется о стенки, чем больше их масса, скорость и сила воздействия на стенки сосуда– тем выше показатель давления.
Классификация
Физики различают атмосферное, абсолютное и избыточное давление. Эти виды величин связаны между собой посредством физических формул.
Единицы измерения давления
Существует множество традиционных единиц давления, которые сложились в результате развития физических дисциплин. Наиболее распространенными их них являются «бар», «атмосфера», “мм ртутного столба” и другие производные от них величины. В физических процессах этот параметр обозначается литерой Р, измеряется в паскалях и производных от него единицах. В письменном виде паскаль отображается так: [Па].
Понятие атмосферного давления
Окружающий нас воздух состоит из постоянно движущихся молекул, которые сталкиваются с земной поверхностью,находящимися на ней предметами и между собой. Из ударов крохотных частиц складывается итоговое давление. Данный параметр называется атмосферными, или барометрическим давлением.
Но, как показали измерения, Ратм в значительной степени зависит от температуры окружающей среды и высоты над уровнем моря. Поэтому для объяснения физических процессов и решения задач текущие параметры атмосферного давления сводят к нормальным условиям. Начальные параметры Ратм определяются при показателе температуры 0⁰ С над нулевым уровнем моря.
Что такое абсолютное давление
Стандартные способы измерения давления обычно используют атмосферное давление в качестве точки отсчета. Обычно этот параметр измеряется различными приборами. Наиболее популярными из которых являются барометры.

В других случаях применяют отношение наблюдаемого давления к вакууму или к другой выбранной отметке. Чтобы обозначить выбранные категории, применяют такие определения:
- Абсолютное давление газа: является параметром точки перехода между вакуумом и наблюдаемым давлением.
- Избыточное давление: для него точкой отсчета становится давление атмосферное. Вычисляется этот показатель как разность между абсолютным и атмосферным давлением.
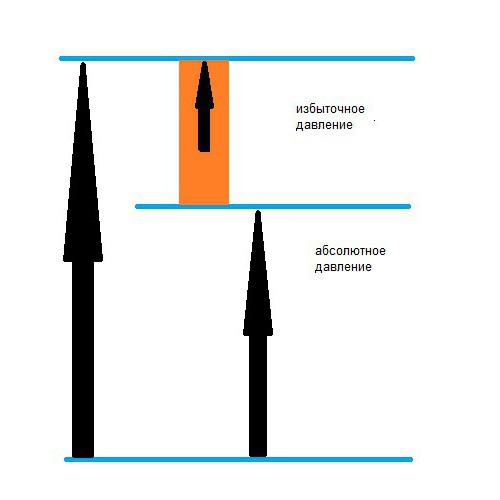
- Дифференциальное давление – является разностью показателей между двумя произвольными точками измерений.
Дифференциальное, абсолютное и избыточное давление визуально может быть представлено так:
Избыточное и абсолютное давление логически связаны между собой. Значение абсолютного давления можно получить, измерив наблюдаемое давление и прибавив к нему величину атмосферного Р.
В случае избыточного давления точкой отсчета служит значение атмосферного P. Таким образом, эта величина может быть представлена как разность между абсолютным давлением и атмосферным. Абсолютное и избыточное давление не может быть отрицательным. При Рабс=0 давление становится равным атмосферному показателю этой величины. Если быть точным, то Рабс не может быть равно вакууму – всегда остается какая-то величина, сформированная, например, давлением насыщенных паров в жидкости. Но в случае тяжелых жидкостей этот параметр очень незначителен, поэтому в первоначальных расчетах, не требующих точного вычисления, вполне допустимо.
Что такое абсолютное давление воздуха
Абсолютное давление воздуха можно измерить лишь в сосудах с другими веществами – с жидкостями или газами. Так, данный параметр довольно часто измеряется в закрытых сосудах с жидкостями. Как и в первом случае, абсолютное давление воздуха в закрытом сосуде можно измерить,как разницу между наблюдаемым Р и атмосферным.
Пьезометрическая высота
Как это часто бывает, наряду с общепринятыми единицами измерения физических величин, используются и исторические. Пьезометрическая высота -это одна из таких величин. Она может быть измерена специальным прибором, представляющим собой стеклянную трубку, верхняя часть которой незапечатана и открыто сообщается с атмосферой, а нижняя присоединена к сосуду, в котором измеряется давление. Прибор, при помощи которого можно провести подобные измерения, представлен ниже:
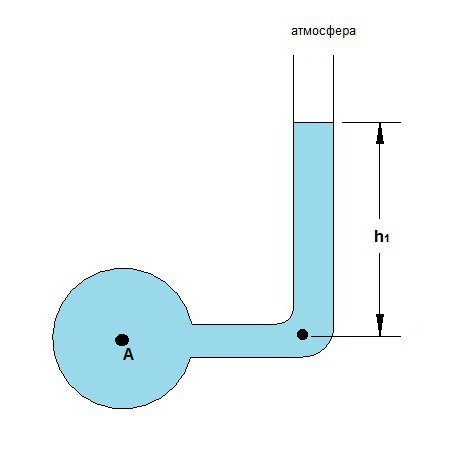
Если к давлению, наблюдаемому в сосуде, применить законы гидростатики, можно получить такое выражение для абсолютного давления:
Здесь ра – атмосферное давление, а выражение gρhp представляет собой произведение высоты столба жидкости на ее плотность и на значение силы тяжести. Так можно измерить абсолютное значение газа в любом сосуде.
Источник

1. Твёрдые тела оказывают давление на опору. На тело, стоящее на опоре, действуют сила тяжести ( vec{F}_т=mvec{g} ) и сила реакции опоры ( vec{N} ) (рис. 55).
Если опора неподвижна, то это тело действует на неё с силой ( vec{F} ), называемой силой давления и равной в этом случае по модулю силе тяжести: ( F=mg ).
Физическая величина, равная отношению силы давления ( F ) к площади поверхности ( S ) называется давлением и обозначается буквой ( p ):
[ p=F/S ]
Единицей давления является 1 паскаль (1 Па):
[ [,p,]=1Н/1м^2=1,Н/м^2=1,Па ]
Более крупная единица давления — килопаскаль.
[ 1, кПа = 1000, Па ]
Как видно из формулы, давление на поверхность зависит от площади поверхности. Так, человек проваливается в снег при ходьбе по нему и спокойно перемещается на лыжах. В том случае, когда нужно увеличить давление на твёрдое тело, используют заострённые предметы, например, булавки, гвозди, ножи и т.п.
2. Жидкости и газы тоже оказывают давление на сосуд, в котором они находятся. Так, молекулы газа, находящегося в воздушном шаре, непрерывно движутся и при этом соударяются со стенками шара. Эти удары и вызывают давление газа на стенки шара и любого другого сосуда, в котором газ находится. Удар одной молекулы слаб, но внутри шара находится огромное число молекул, поэтому
их суммарное давление на стенки шара ощутимо.
Чем выше температура газа, чем с большей скоростью движутся молекулы и чем чаще и сильнее ударяются они о стенки сосуда, тем, следовательно, давление газа на стенки сосуда больше.
Если уменьшить объём газа в сосуде, не меняя его массу, то число молекул в единице объёма увеличится, увеличится и плотность газа. Число ударов молекул о стенки сосуда при этом возрастёт, следовательно, увеличится давление газа. При увеличении объёма газа при той же массе уменьшится его плотность и число ударов молекул о стенки сосуда. Давление уменьшится.
Таким образом, давление газа тем больше, чем выше его температура и меньше объём при неизменной массе. При повышении температуры и уменьшении объёма молекулы с большей силой и чаще ударяются о стенки сосуда.
3. Опыт показывает, что давление, производимое на жидкость или газ, передаётся по всем направлениям. Если шар с отверстиями, соединённый с трубкой, внутри которой находится поршень, наполнить водой, а затем нажать на поршень, то можно заметить, что вода брызнет из всех отверстий. При этом струйки вытекающей воды будут примерно одинаковыми. Это говорит о том, что давление, которое мы создаём, действуя на воду, передаётся водой по всем направлениям одинаково. Тот же эффект можно наблюдать, если шар заполнить дымом. Дым тоже будет передавать производимое на него давление по всем направлениям одинаково.
То, что газы и жидкости передают давление по всем направлениям, объясняется подвижностью их молекул. Она проявляется в том, что слои и частицы жидкостей и газов могут свободно перемещаться друг относительно друга но разным направлениям. Благодаря подвижности молекул давление, которое оказывает поршень на ближайший к нему слой, передаётся последующим слоям. Молекулы газа и жидкости движутся хаотически, поэтому и их действие распределяется равномерно по всему объёму шара. Таким образом, давление, производимое на жидкость или газ, передаётся по всем направлениям без изменения в каждую точку жидкости или газа. Это утверждение называется законом Паскаля.
4. Закон Паскаля находит применение в гидравлических машинах.
Основной частью любой гидравлической машины являются два соединенных между собой цилиндра разного диаметра. Цилиндры заполнены жидкостью, чаще всего маслом, и в них помещены поршни.
Пусть на большой поршень площадью ( S_1 ) действует сила ( F_1 ) (рис. 56). Эта сила будет оказывать на поршень давление ( p_1 ): ( p_1=F_1/S_1 ).
Это давление ( p_1 ) будет передаваться жидкости, находящейся под большим поршнем. Согласно закону Паскаля, давление, производимое на жидкость или газ, передаётся по всем направлениям без изменения. Следовательно, давление будет передаваться жидкости, находящейся под меньшим поршнем, и на меньший поршень со стороны жидкости будет действовать давление ( p_2=p_1 ). Соответственно, на меньший поршень со стороны жидкости будет действовать сила ( F_2=p_2S_2 ), направленная вверх. Откуда ( p_2=F_2/S_2 ).
Чтобы жидкость и поршни находились в равновесии, на меньший поршень следует подействовать силой, равной по модулю силе ( F_2 ), направленной вертикально вниз. Для этого можно, например, положить на поршень груз.
Так как ( p_1=p_2 ), то ( F_1/S_1=F_2/S_2 ) или ( F_1/F_2=S_1/S_2 ).
Таким образом, гидравлическая машина даёт выигрыш в силе во столько раз, во сколько раз площадь большего поршня больше площади меньшего поршня.
Это означает, что с помощью некоторой силы, приложенной к малому поршню гидравлической машины, можно уравновесить существенно большую силу, приложенную к большему поршню.
Гидравлическая машина, так же как и любой простой механизм, даёт выигрыш в силе, но не даёт выигрыша в работе.
5. Твёрдые тела производят давление на опору вследствие действия на них силы тяжести. Поскольку на жидкости тоже действует сила тяжести, то и жидкости оказывают давление на дно сосуда. Это можно доказать экспериментально.
Если в трубку, дно которой затянуто плёнкой, налить воду, то плёнка заметно прогнётся. Это происходит потому, что на воду действует сила тяжести, и каждый слой воды давит на слои воды, лежащие ниже, и соответственно на дно сосуда.
Давление производится жидкостью не только на дно сосуда, оно существует внутри жидкости на любой её глубине. При этом производимое давление передаётся по закону Паскаля по всем направлениям одинаково.
Если в трубку с дном, затянутым плёнкой, добавить воды, то плёнка прогнётся сильнее. Это происходит потому, что увеличивается вес воды и соответственно давление воды на дно трубки. Таким образом, давление жидкости на дно сосуда тем больше, чем больше высота столба жидкости.
Если теперь в трубку до той же высоты налить масло, плотность которого меньше плотности воды, то плёнка прогнётся меньше, чем в том случае, когда в ней была вода (рис. 57 а). Это означает, что давление на дно сосуда тем больше, чем больше плотность жидкости.
Сила ( F ), с которой жидкость давит на дно, равна её весу ( P ). Вес жидкости ( P ) равен произведению её массы ( m ) и ускорения свободного падения ( g ): ( F=P=mg ).
Масса жидкости ( m ) равна произведению её плотности ( rho ) и объёма ( V ): ( m=rho V ), где ( V=Sh ) (рис. 57 б). Тогда ( F=mg=rho V!g=rho Shg ).
Разделив вес жидкости (силу, с которой она давит на дно сосуда) на площадь дна, получим давление жидкости ( p ): ( p=F/S ) или ( p=rho gSh/S ), т.е. ( p=rho gh )
Давление жидкости на дно и стенки сосуда равно произведению плотности жидкости, ускорения свободного падения и высоты столба жидкости.
6. Два или более сосудов, соединённых между собой у дна, называются сообщающимися сосудами. Примерами сообщающихся сосудов могут служить гидравлические машины и жидкостный манометр. Самым простым сообщающимся сосудом, которым вы пользуетесь каждый день, является чайник.
Если две стеклянные трубки соединить резиновой трубкой (рис. 57 в), то получатся сообщающиеся сосуды. Наливая в одну трубку воду, можно заметить, что она будет перетекать и в другую трубку. При этом уровни воды в трубках будут все время одинаковы.
Можно поднять одну из трубок или наклонить ее, в любом случае друг относительно друга уровни воды или любой другой жидкости останутся одинаковыми, т.е. будут лежать в одной и той же горизонтальной плоскости.
Можно сделать вывод: в сообщающихся сосудах поверхности однородной жидкости всегда устанавливаются на одном уровне.
Это верно при условии, что давление на поверхность жидкости одинаково. При использовании сообщающихся сосудов в качестве жидкостного манометра именно по разности уровней жидкости в трубках можно судить о значении давления.
Объяснить то, что в сообщающихся сосудах однородная жидкость устанавливается на одном уровне, можно следующим образом. Жидкость в сосудах не перемещается, следовательно, её давления в сосудах на одном уровне, в том числе и на дно, одинаковы. Она имеет одинаковую плотность, т.к. она однородная. Следовательно, в соответствии с формулой ( p=rho gh ) высоты жидкости тоже одинаковы.
Если в одну трубку налить воду, а в другую масло, плотность которого меньше плотности воды, то уровень воды будет ниже, чем уровень масла в другой трубке (рис. 58).
Это объясняется тем, что давление жидкости на дно сосуда зависит от высоты столба жидкости и от её плотности. При одинаковом давлении, чем больше плотность жидкости, тем меньше высота её столба. Поскольку плотность масла меньше плотности воды, то столб масла выше столба воды. Жидкости, имеющие разную плотность, устанавливаются в сообщающихся сосудах на разных уровнях; во сколько раз плотность одной жидкости больше плотности другой, во столько раз меньше высота её столба.
7. Земля окружена воздушной оболочкой — атмосферой. Воздух, как и газы, входящие в состав атмосферы, имеет массу. Соответственно, на него действует сила тяжести, и он оказывает давление на поверхность Земли.
Давление воздушной оболочки на поверхность Земли и находящиеся на ней тела называется атмосферным давлением.
В существовании атмосферного давления легко убедиться на опытах. Если опустить в воду трубку с плотно прилегающим к её стенкам поршнем и поднимать поршень вверх, то вода будет подниматься по трубке вслед за поршнем.
Это происходит потому, что при подъёме поршня между ним и поверхностью воды образуется разреженное пространство. На поверхность воды в сосуде действует атмосферное давление, которое в соответствии с законом Паскаля передаётся по всем направлениям, в том числе и в направлении трубки. Оно и заставляет воду подниматься за поршнем.
Для расчёта атмосферного давления нельзя использовать формулу, по которой рассчитывается давление столба жидкости, так как для этого нужно знать высоту атмосферы и плотность воздуха. Но атмосфера не имеет определённой границы, а плотность воздуха изменяется с высотой. Однако атмосферное давление можно измерить.
Опыт по измерению атмосферного давления был предложен итальянским ученым Торричелли в XVII в. Стеклянную трубку длиной 1 м, запаянную с одного конца, заполнили ртутью. Закрыв другой конец трубки, её перевернули и опустили в сосуд с ртутью. Затем этот конец трубки открыли, и часть ртути вылилась из неё в сосуд, а часть осталась в трубке. Высота столба ртути, оставшейся в трубке, оказалась равной примерно 760 мм.
Объясняется это следующим образом: атмосферное давление действует на ртуть в сосуде, это давление передаётся по всем направлениям и действует на ртуть в основании трубки снизу вверх. Это давление уравновешивает давление столба ртути в трубке. Таким образом, атмосферное давление равно давлению, которое оказывает у основании трубки столб ртути высотой 760 мм. Это давление называют нормальным атмосферным давлением.
Если атмосферное давление выше нормального, то высота столба ртути больше, если — меньше нормального, то столб ртути опустится ниже.
Нормальное атмосферное давление равно 101 300 Па.
Атмосферное давление чаще выражают не в паскалях, а в миллиметрах ртутного столба (мм рт.ст.). 1 мм рт.ст. = 133,3 Па.
Если к трубке в опыте Торричелли прикрепить шкалу и проградуировать её в миллиметрах, то получим прибор — ртутный барометр, с помощью которого можно измерять атмосферное давление.
В быту и технике для измерения атмосферного давления применяют более удобный в обращении металлический барометр, называемый анероидом.
Атмосферное давление зависит от высоты. Это объясняется тем, что воздух хорошо сжимаем, так же как и все газы. Верхние слои воздуха давят на лежащие ниже и сжимают их, соответственно плотность слоёв воздуха, а следовательно и давление, у поверхности Земли больше, чем на некоторой высоте от неё.
Так, в местности, лежащей на уровне моря, давление равно примерно 760 мм рт. ст., т.е. нормальному атмосферному. В горах оно выше. Измерения показывают, что на каждые 12 м подъёма атмосферное давление уменьшается примерно на 1 мм рт.ст.
8. Если подвешенный к пружине динамометра шарик опустить в сосуд с водой, то можно заметить, что показание динамометра уменьшится.
Точно так же можно изменить показания динамометра, если подействовать на шарик рукой снизу вверх. Следовательно, когда шарик опустили в воду, на него, помимо силы тяжести и силы упругости пружины динамометра, стала действовать сила, направленная вверх. Эту силу называют выталкивающей или архимедовой силой.
Выталкивающая сила возникает за счёт разности давления воды на нижнюю поверхность шарика и давления на его верхнюю поверхность, поскольку давление жидкости зависит от высоты её столба.
Сила давления ( F_1 ), действующая на верхнюю поверхность шарика, направлена вниз, сила давления ( F_2 ), действующая на нижнюю поверхность шарика, направлена вверх. Так как ( F_2 ) больше ( F_1 ), то результирующая этих двух сил, являющаяся выталкивающей силой, будет направлена вверх.
Выталкивающая сила тем больше, чем больше плотность жидкости, в которую погружено тело, и чем больше объём тела, погружённого в жидкость.
Опыт показывает, что выталкивающая сила ( F ) может быть вычислена по формуле: ( F=rho gV ), где ( rho ) — плотность жидкости, в которую погружено тело, ( V ) — объём погружённой части тела.
Выталкивающая сила равна произведению плотности жидкости, ускорения свободного падения и объёма погружённой части тела.
Этот закон называют законом Архимеда.
В воздухе, так же как и в любом другом газе, на тело действует выталкивающая сила. Она имеет ту же природу, что и выталкивающая сила, действующая на тело в жидкости. Её происхождение обусловлено разностью давлений на нижнюю и верхнюю грани тела. Однако, поскольку плотность газа намного меньше плотности жидкости, выталкивающая сила, действующая на тело, в газе меньше, чем в жидкости. Часто при решении задач пренебрегают выталкивающей силой, действующей на тело в воздухе, и считают, что вес покоящегося тела в воздухе равен по модулю действующей на него силе тяжести.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Ребёнка везут на санках по свежевыпавшему снегу. Какие санки — с широкими или узкими полозьями — следует выбрать, чтобы не проваливаться в снег?
1) с широкими
2) с узкими
3) безразлично
4) ответ зависит от веса санок
2. Брусок в форме прямоугольного параллелепипеда положили на стол сначала узкой гранью (1), а затем — широкой (2). Сравните силы давления (( F_1 ) и ( F_2 )) и давления (( p_1 ) и ( p_2 )), производимые бруском на стол в этих случаях.
1) ( F_1=F_2; p_1>p_2 )
2) ( F_1=F_2; p_1<p_2 )
3) ( F_1<F_2; p_1<p_2 )
4) ( F_1=F_2; p_1=p_2 )
3. Сила ( F_1 ), действующая со стороны жидкости на один поршень гидравлической машины, в 16 раз меньше силы ( F_2 ), действующей на другой поршень. Как соотносятся модули работы ( (A_1) ) и ( (A_2) ) этих сил, совершаемой при перемещении поршней? Трением пренебречь.
1) ( A_1=A_2 )
2) ( A_1=16A_2 )
3) ( A_2=16A_1 )
4) ( A_1=4A_2 )
4. В сосуды различной формы налита одна и та же жидкость. Высота уровня жидкости во всех сосудах одинакова. В каком из сосудов давление на дно наименьшее?
1) в сосуде А
2) в сосуде Б
3) в сосуде В
4) во всех сосудах одинаковое
5. Стеклянный сосуд, правое колено которого запаяно, заполнен жидкостью плотностью с (см. рисунок). Давление, оказываемое жидкостью на дно сосуда в точке Б, равно
1) ( rho gh_3 )
2) ( rho gh_1 )
3) ( rho g(h_1-h_2) )
4) ( rho gh_2 )
6. Атмосферное давление на вершине горы Казбек
1) меньше, чем у её подножия
2) больше, чем у её подножия
3) равно давлению у её подножия
4) может быть больше или меньше, чем у её подножия, в зависимости от погоды
7. В открытых сосудах 1 и 2 находятся соответственно ртуть и вода. Если открыть кран К, то
1) ни вода, ни ртуть перетекать не будут
2) вода начнёт перетекать из сосуда 2 в сосуд 1
3) перемещение жидкостей будет зависеть от атмосферного давления
4) ртуть начнёт перетекать из сосуда 1 в сосуд 2
8. Два однородных шара, один из которых изготовлен из стали, а другой — из олова, уравновешены на рычажных весах (см. рисунок). Нарушится ли равновесие весов,
если шары опустить в воду?
1) Равновесие весов не нарушится, так как шары одинаковой массы.
2) Равновесие весов нарушится — перевесит шар из стали.
3) Равновесие весов нарушится — перевесит шар из олова.
4) Равновесие весов не нарушится, так как шары опускают в одну и ту же жидкость.
9. Алюминиевый шар, подвешенный на нити, опущен в крепкий раствор поваренной соли. Затем шар перенесли из раствора поваренной соли в дистиллированную воду. При этом сила натяжения нити
1) может остаться неизменной или измениться в зависимости от объёма шара
2) не изменится
3) увеличится
4) уменьшится
10. Теплоход переходит из устья реки в солёное море. При этом архимедова сила, действующая на теплоход,
1) увеличится
2) уменьшится или увеличится в зависимости от размера теплохода
3) не изменится
4) уменьшится
11. Шарик, опущенный в жидкость, начинает опускаться на дно. Как по мере движения шарика в жидкости изменяются выталкивающая сила, действующая на него, вес шарика, давление жидкости? Установите соответствие между физическими величинами и характером их изменения. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) выталкивающая сила
Б) вес
B) давление жидкости
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИН
1) увеличивается
2) уменьшается
3) не изменяется
12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) атмосферное давление можно рассчитать так же, как давление жидкости на дно сосуда.
2) в опыте Торричелли можно ртуть заменить водой при той же длине трубки.
3) для того, чтобы столб воды производил на дно сосуда такое же давление, что и столб керосина, его высота должна составлять 0,8 от высоты столба керосина.
4) на вершине горы атмосферное давление меньше, чем у её подножия.
5) закон Паскаля справедлив для газов, жидкостей и твёрдых тел.
Часть 2
13. Камень весит в воздухе 6 Н, а в воде 4 Н. Чему равен объём этого камня?
Ответы
Давление. Атмосферное давление. Закон Паскаля. Закон Архимеда
2.8 (55%) 4 votes
Источник