Расчет тонкостенных цилиндрических сосудов
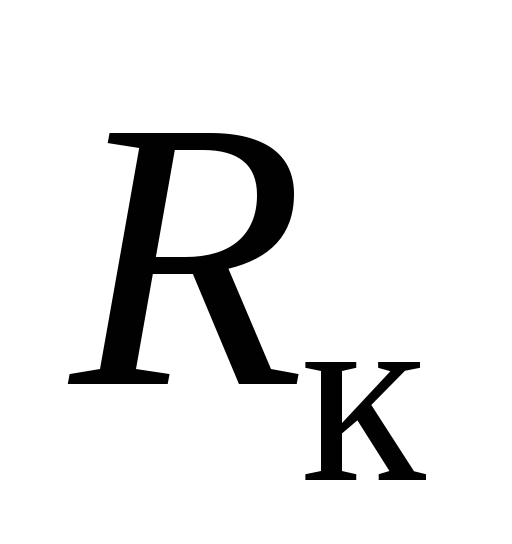
Тонкостенные цилиндрические сосуды, подверженные внутреннему давлению, имеют весьма широкое распространение в технике (трубопроводы, котлы и различного рода емкости, заполненные жидкостью или газом). Основной задачей при расчетах таких сосудов является определение необходимой толщины их стенок.
Пусть имеется горизонтальный трубопровод (рис. 17) внутренним диаметром , заполненный жидкостью, находящейся под избыточным давлением(изменение давления по вертикали незначительно, поэтому им пренебрегаем). Под влиянием этого давления стенки трубопровода испытывают действие разрывающего усилия, стремящегося разорвать трубопровод по его образующей. Таким образом, стенки трубопровода будут работать на растяжение.
Рис. 17. К определению толщины стенок труб, воспринимающих внутреннее давление жидкости
Составим для участка трубопровода длиной уравнение прочности
, (46)
где | – разрывающее усилие, Н; | |
– допустимое напряжение на растяжение, МПа; | ||
– площадь сечения стенок трубы, по которой возможен разрыв, . |
Так как поперечное сечение трубы симметрично относительно ее оси, достаточно рассмотреть разрывающее усилие в какой-нибудь одной плоскости. Разрывающее усилие, очевидно, представит собой силу давления на полуцилиндрическую поверхность и будет равно давлению на проекцию этой поверхности на плоскость, нормальную к направлению разрывающего усилия, т.е.
.
Так как разрыв стенок трубы возможен одновременно по двум сечениям 1 – 1 и 2 – 2, площадь сечения, по которому возможен разрыв
,
где – искомая толщина стенки трубы (сосуда).
Подставляя полученные значения в исходное расчетное уравнение, получим
,
откуда
. (47)
Для вертикального цилиндрического сосуда (резервуара) диаметром , высотой, заполненного до краев жидкостью (рис. 18), разрывающее усилие определяется как горизонтальная составляющая полного давления на полуцилиндрическую поверхность (равная давлению на проекцию это поверхности на вертикальную плоскость).
При этом изменением давления по высоте пренебрегают и ведут расчет по наибольшему давлению у основания сосуда. Если же сосуд состоит из ряда отдельных поясов, за расчетное давление для каждого пояса принимают давление у нижней его кромки.
Таким образом, получаем
.
Рис. 18. Вертикальный цилиндрический сосуд
Для определения толщины стенок имеем условие
,
откуда
. (48)
Определим толщину стенок сосуда из условия сопротивления разрывающему усилию, направленному вдоль оси сосуда (рис. 19). Разрывающее усилие в этом случае определяется произведением гидростатического давления в в сосуде у его крышки или днища на проекцию поверхности этой крышки на плоскость, нормальную к оси сосуда,
.
Рис. 19. Сосуд воспринимающий разрывающее
усилие вдоль оси.
Сечение же, по которому возможен отрыв крышки от цилиндрической части сосуда, определяется выражением
.
Следовательно
и толщина стенок
. (49)
т.е. получается в два раза меньше, чем в первом случае.
Таким образом, наиболее опасным с точки зрения прочности является разрыв сосуда в продольном направлении, и поэтому толщину стенок следует определять по формуле (47); выражение же (49) применяется при расчетах поперечных швов.
Необходимо иметь в виду, что полученные здесь зависимости применимы без поправок лишь к расчетам цельнотянутых или сварных сосудов. В случае клепанных сосудов необходимо учитывать неизбежное ослабление материала склепываемых листов заклепочным швом введением в расчетные формулы коэффициента прочности заклепочного шва . Значение этого коэффициента устанавливается в зависимости от типа заклепочного шва и представляет собой отвлеченное число, всегда меньшее единицы (). Кроме того, принимая во внимание неизбежность коррозии и требования технологии процесса клепки, получаемую расчетом толщину стенок еще несколько увеличивают на так называемый производственный припуск.
С учетом припуска формулы (47) и (49) принимают вид
.
Для определения результирующей силы , действующей в колене трубы рассмотрим рис. 20.
, (50)
Так как силы направлены под углом α, то сила
. (51)
Влиянием веса труб в расчетах пренебрегаем.

Рис. 20. К определению силы в колене трубы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Если толщина стенок цилиндра мала по сравнению с радиусами и , то известное выражение для тангенцальных напряжений приобретает вид
т. е. величину, определенную нами раньше (§ 34).
Для тонкостенных резервуаров, имеющих форму поверхностей вращения и находящихся под внутренним давлением р, распределенным симметрично относительно оси вращения, можно вывести общую формулу для вычисления напряжений.
Выделим (Рис.1) из рассматриваемого резервуара элемент двумя смежными меридиональными сечениями и двумя сечениями, нормальными к меридиану.
Рис.1. Фрагмент тонкостенного резервуара и его напряженное состояние.
Размеры элемента по меридиану и по перпендикулярному к нему направлению обозначим соответственно и , радиусы кривизны меридиана и перпендикулярного к нему сечения обозначим и , толщину стенки назовем t.
По симметрии по граням выделенного элемента будут действовать только нормальные напряжения в меридиальном направления и в направлении, перпендикулярном к меридиану. Соответствующие усилия, приложенные к граням элемента, будут и . Так как тонкая оболочка сопротивляется только растяжению, подобно гибкой нити, то эти усилия будут направлены по касательной к меридиану и к сечению, нормальному к меридиану.
Усилия (Рис.2) дадут в нормальном к поверхности элемента направлении равнодействующую ab, равную
Рис.2. Равновесие элемента тонкостенного резервуара
Подобным же образом усилия дадут в том же направлении равнодействующую Сумма этих усилий уравновешивает нормальное давление, приложенное к элементу
Отсюда
Это основное уравнение, связывающее напряжения и для тонкостенных сосудов вращения, дано Лапласом.
Так как мы задались распределением (равномерным) напряжений по толщине стенки, то задача статически определима; второе уравнение равновесия получится, если мы рассмотрим равновесие нижней, отрезанной каким-либо параллельным кругом, части резервуара.
Рассмотрим случай гидростатической нагрузки (рис.3). Меридиональную кривую отнесем к осям х и у с началом координат в вершине кривой. Сечение проведем на уровне у от точки О. Радиус соответствующего параллельного круга будет х.
Рис.3. Равновесие нижнего фрагмента тонкостенного резервуара.
Каждая пара усилий , действующих на диаметрально противоположные элементы проведенного сечения, дает вертикальную равнодействующую bс, равную
сумма этих усилий, действующих по всей окружности проведенного сечения, будет равна ; она будет уравновешивать давление жидкости на этом уровне плюс вес жидкости в отрезанной части сосуда .
Отсюда
Зная уравнение меридиональной кривой, можно найти , х и для каждого значения у, и стало быть, найти , а из уравнения Лапласа и
Например, для конического резервуара с углом при вершине , наполненного жидкостью с объемным весом у на высоту h, будем иметь:
тогда
Для сферического сосуда радиусом , находящегося под внутренним давлением , по симметрии ; тогда из уравнения (Лапласа), так как
и
Если меридиональная кривая будет иметь переломы с разрывом непрерывности угла , то равновесие тонкой оболочки у места перелома может быть обеспечено лишь наличием реакций, приложенных к оболочке по окружности в этом месте. Появление таких реакций обеспечивается устройством специальных колец, способных брать на себя усилия, возникающие в них в связи с неуравновешенностью напряжений по обе стороны точки перелома.
Дальше…
Источник
13.1. Понятие о безмоментной теории расчета тонкостенных сосудов
В инженерной практике широкое применение находят такие конструкции, как цистерны, водонапорные резервуары, газгольдеры, воздушные и газовые баллоны, купола зданий, аппараты химического машиностроения, части корпусов турбин и реактивных двигателей и т.д. Все эти конструкции с точки зрения их расчета на прочность и жесткость могут быть отнесены к тонкостенным сосудам (оболочкам) (Рис.13.1,а).
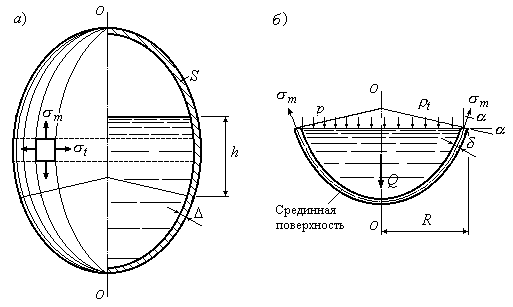
Рис.13.1
Характерной особенностью большинства тонкостенных сосудов является то, что по форме они представляют тела вращения, т.е. их поверхность может быть образована вращением некоторой кривой  вокруг осиО-О. Сечение сосуда плоскостью, содержащей ось О-О, называется меридиональным сечением, а сечения, перпендикулярные к меридиональным сечениям, называются окружными. Окружные сечения, как правило, имеют вид конуса. Показанная на рис 13.1б нижняя часть сосуда отделена от верхней окружным сечением. Поверхность, делящая толщину стенок сосуда пополам, называется срединной поверхностью. Считается, что оболочка является тонкостенной, если отношение наименьшего главного радиуса кривизны в данной точке поверхности к толщине стенки оболочки превышает число 10
вокруг осиО-О. Сечение сосуда плоскостью, содержащей ось О-О, называется меридиональным сечением, а сечения, перпендикулярные к меридиональным сечениям, называются окружными. Окружные сечения, как правило, имеют вид конуса. Показанная на рис 13.1б нижняя часть сосуда отделена от верхней окружным сечением. Поверхность, делящая толщину стенок сосуда пополам, называется срединной поверхностью. Считается, что оболочка является тонкостенной, если отношение наименьшего главного радиуса кривизны в данной точке поверхности к толщине стенки оболочки превышает число 10 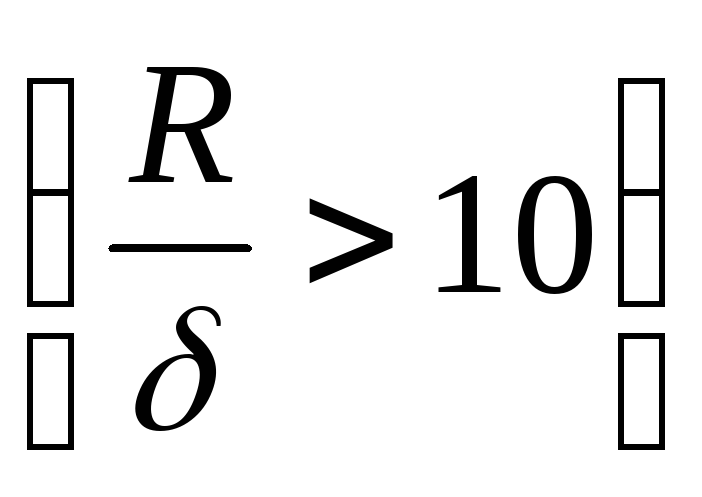 .
.
Рассмотрим общий случай действия на оболочку какой-либо осесимметричной нагрузки, т.е. такой нагрузки, которая не меняется в окружном направлении и может меняться лишь вдоль меридиана. Выделим из тела оболочки двумя окружными и двумя меридиональными сечениями элемент (Рис.13.1,а). Элемент испытывает растяжение во взаимно перпендикулярных направлениях и искривляется. Двустороннему растяжению элемента соответствует равномерное распределение нормальных напряжений по толщине стенки  и возникновение в стенке оболочки нормальных усилий. Изменение кривизны элемента предполагает наличие в стенке оболочки изгибающих моментов. При изгибе в стенке балки возникают нормальные напряжения, меняющиеся по толщине стенки.
и возникновение в стенке оболочки нормальных усилий. Изменение кривизны элемента предполагает наличие в стенке оболочки изгибающих моментов. При изгибе в стенке балки возникают нормальные напряжения, меняющиеся по толщине стенки.
При действии осесимметричной нагрузки влиянием изгибающих моментов можно пренебречь, так как преобладающее значение имеют нормальные силы. Это имеет место тогда, когда форма стенок оболочки и нагрузка на нее таковы, что возможно равновесие между внешними и внутренними усилиями без появления изгибающих моментов. Теория расчета оболочек, построенная на предположении, что нормальные напряжения, возникающие в оболочке, постоянны по толщине и, следовательно, изгиб оболочки отсутствует, называется безмоментной теорией оболочек. Безмоментная теория хорошо работает, если оболочка не имеет резких переходов и жестких защемлений и, кроме того, не нагружена сосредоточенными силами и моментами. Кроме того, эта теория дает более точные результаты, чем меньше толщина стенки оболочки, т.е. чем ближе к истине предположение о равномерном распределении напряжений по толщине стенки.
При наличии сосредоточенных сил и моментов, резких переходов и защемлений сильно усложняется решение задачи. В местах крепления оболочки и в местах резких изменений формы возникают повышенные напряжения, обусловленные влиянием изгибающих моментов. В этом случае применяется так называемая моментная теория расчета оболочек. Следует отметить, что вопросы общей теории оболочек выходят далеко за рамки сопротивления материалов и изучается в специальных разделах строительной механики. В настоящем пособии при расчете тонкостенных сосудов рассматривается безмоментная теория для случаев, когда задача определения напряжений, действующих в меридиональном и окружном сечениях, оказывается статически определимой.
13.2. Определение напряжений в симметричных оболочках по безмоментной теории. Вывод уравнения Лапласа
Рассмотрим осесимметричную тонкостенную оболочку, испытывающую внутреннее давление от веса жидкости (Рис.13.1,а). Двумя меридиональными и двумя окружными сечениями выделим из стенки оболочки бесконечно малый элемент и рассмотрим его равновесие (Рис.13.2).
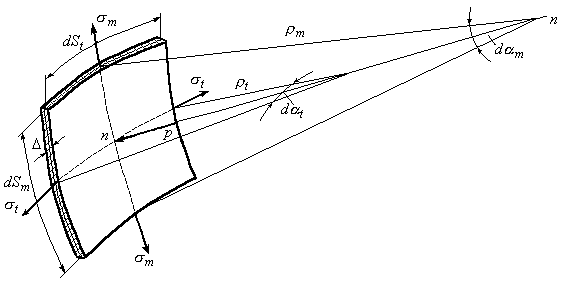
Рис.13.2
В меридиональных и окружных сечениях касательные напряжения отсутствуют ввиду симметрии нагрузки и осутствия взаимных сдвигов сечений. Следовательно, на выделенный элемент будут действовать только главные нормальные напряжения: меридиональное напряжение 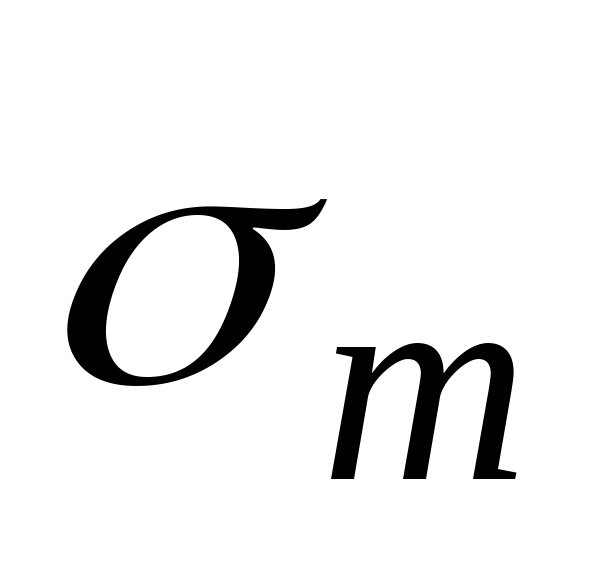 иокружное напряжение
иокружное напряжение  . На основании безмоментной теории будем считать, что по толщине стенки напряжения
. На основании безмоментной теории будем считать, что по толщине стенки напряжения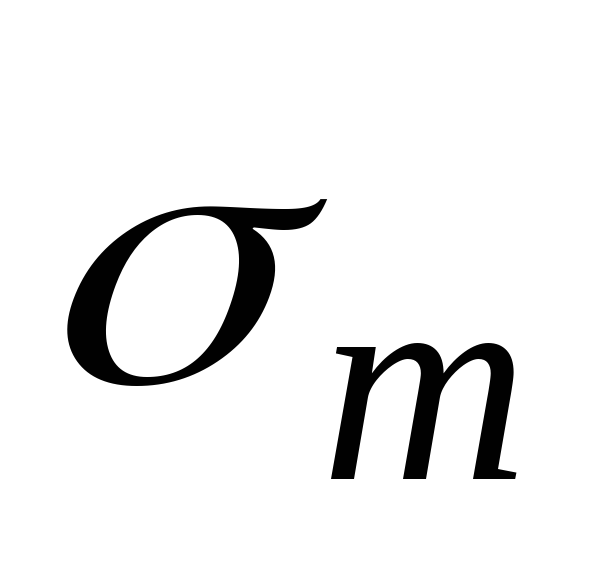 и
и распределены равномерно. Кроме того, все размеры оболочки будем относить к срединной поверхности ее стенок.
распределены равномерно. Кроме того, все размеры оболочки будем относить к срединной поверхности ее стенок.
Срединная поверхность оболочки представляет собой поверхность двоякой кривизны. Радиус кривизны меридиана в рассматриваемой точки обозначим 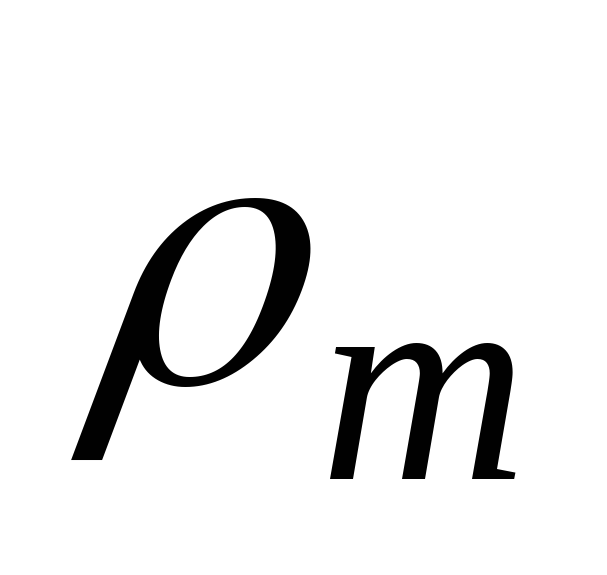 , радиус кривизны срединной поверхности в окружном направлении обозначим
, радиус кривизны срединной поверхности в окружном направлении обозначим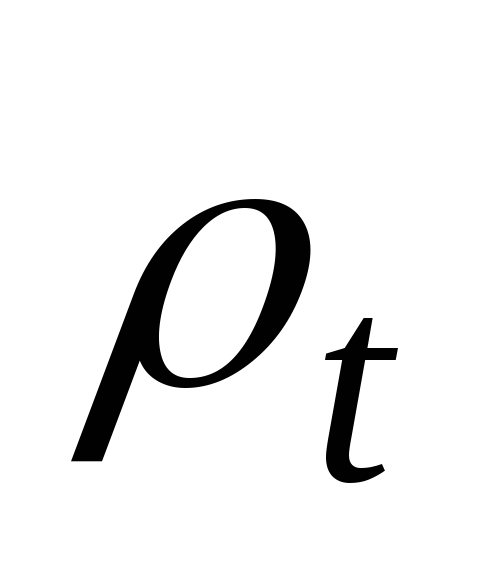 . По граням элемента действуют силы
. По граням элемента действуют силы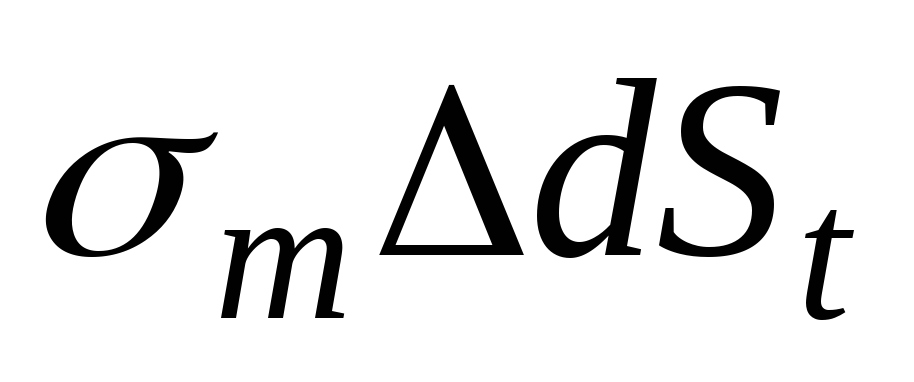 и
и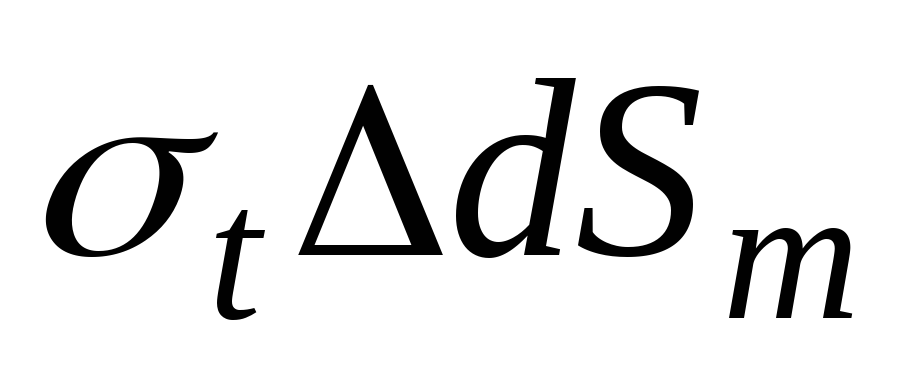 . На внутреннюю поверхность выделенного элемента действует давление жидкости
. На внутреннюю поверхность выделенного элемента действует давление жидкости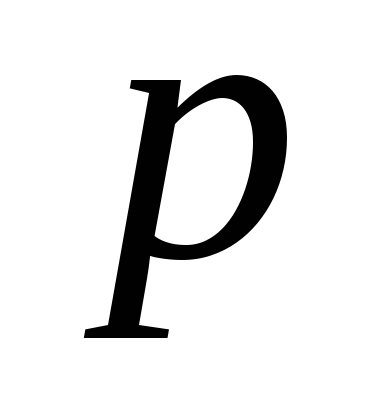 , равнодействующая которого равна
, равнодействующая которого равна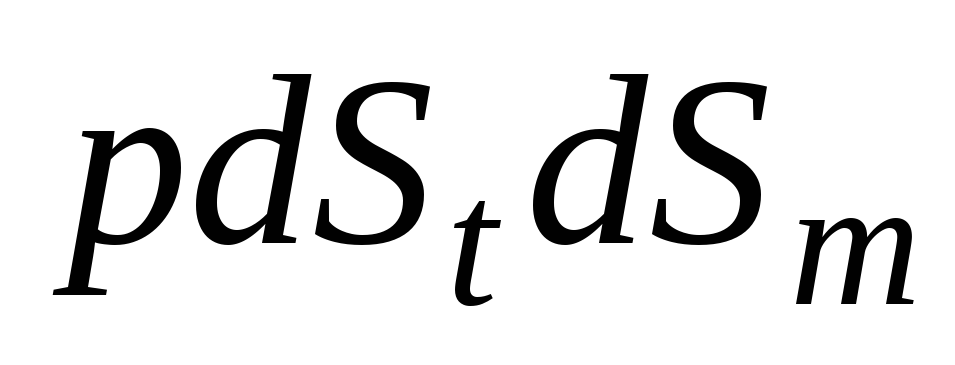 . Спроектируем приведенные выше силы на нормаль
. Спроектируем приведенные выше силы на нормаль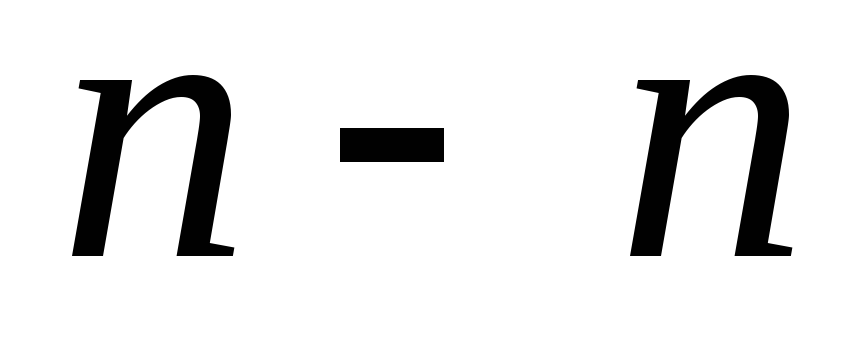 к поверхности:
к поверхности:
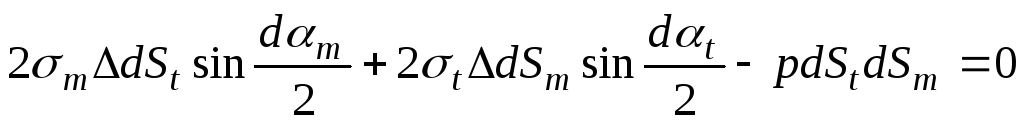 . (а)
. (а)
Изобразим проекцию элемента на меридиональную плоскость (Рис.13.3) и на основании этого рисунка запишем в выражении (а) первое слагаемое. Второе слагаемое записывается по аналогии.
Заменяя в (а) синус его аргументом ввиду малости угла и разделив все члены уравнения (а) на 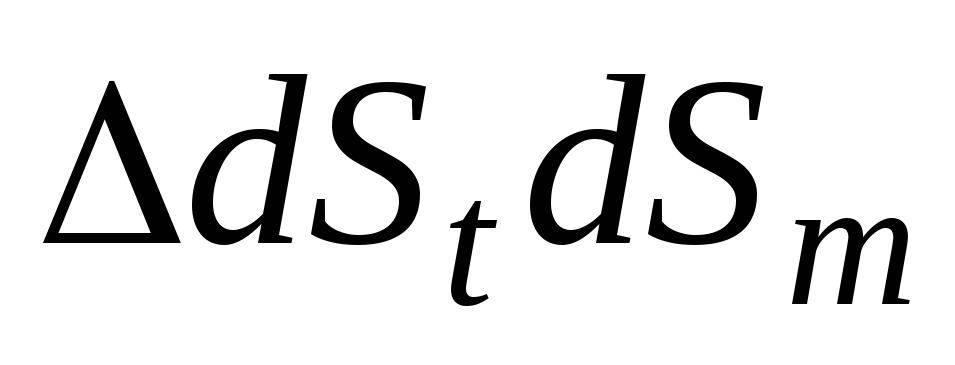 , получим:
, получим:
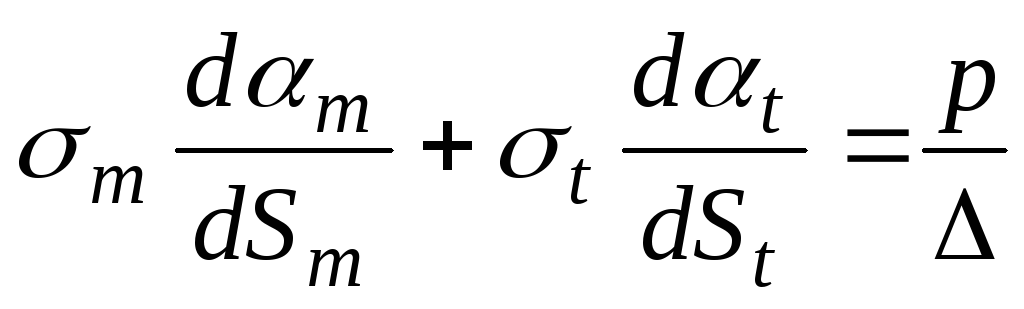 (б).
(б).
Учитывая, что кривизны меридионального и окружного сечений элемента равны соответственно 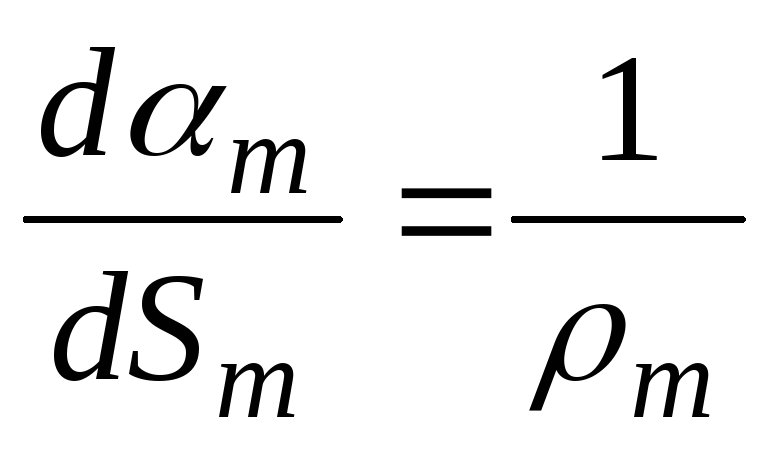 и
и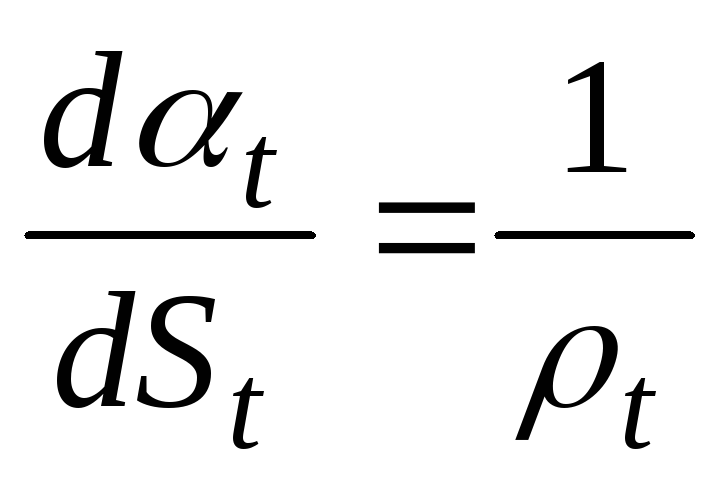 , и подставляя эти выражения в (б) находим:
, и подставляя эти выражения в (б) находим:
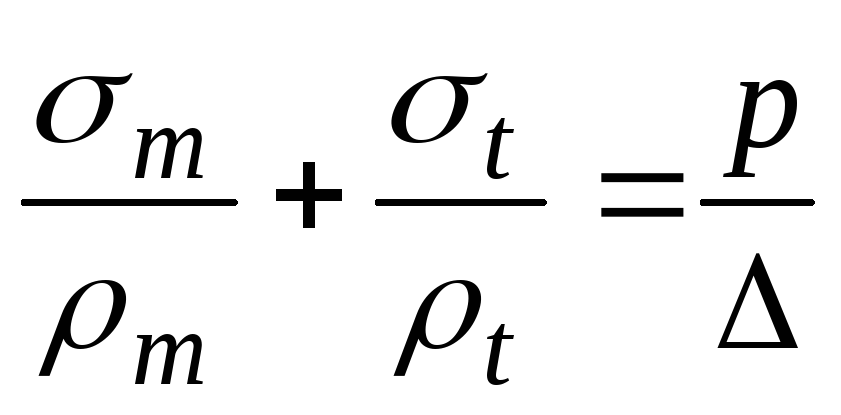 . (13.1)
. (13.1)
Выражение (13.1) представляет собой уравнения Лапласа, названного так в честь французского ученого, который получил его в начале XIXвека при изучении поверхностного натяжения в жидкостях.
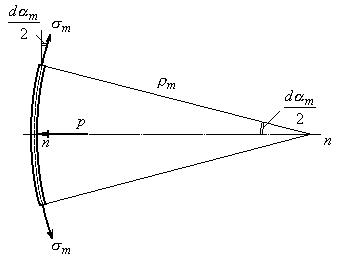
Рис.13.3
В уравнение (13.1) входят два неизвестных напряжения  и
и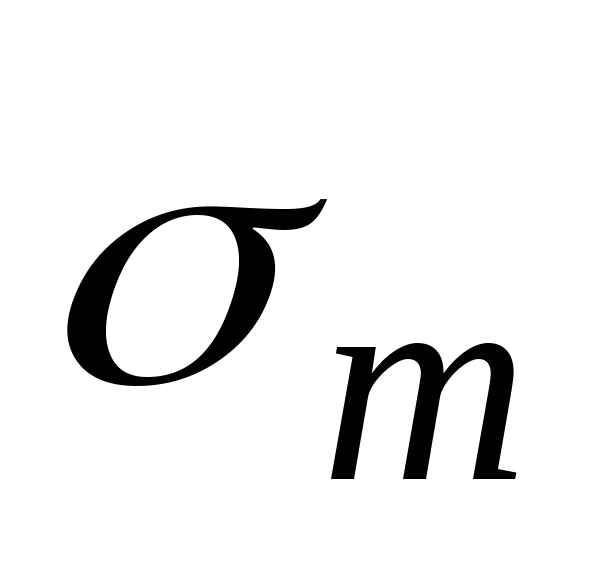 . Меридиональное напряжение
. Меридиональное напряжение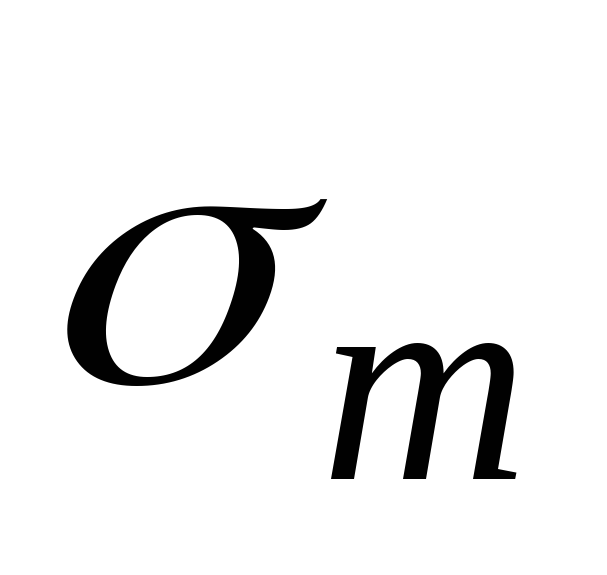 найдем, составив уравнение равновесия на ось
найдем, составив уравнение равновесия на ось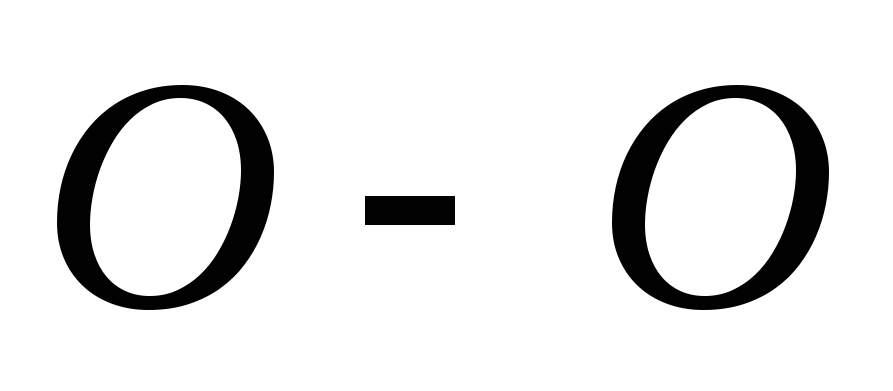 сил, действующих на отсеченную часть оболочки (Рис.12.1,б). Площадь окружного сечения стенок оболочки посчитаем по формуле
сил, действующих на отсеченную часть оболочки (Рис.12.1,б). Площадь окружного сечения стенок оболочки посчитаем по формуле . Напряжения
. Напряжения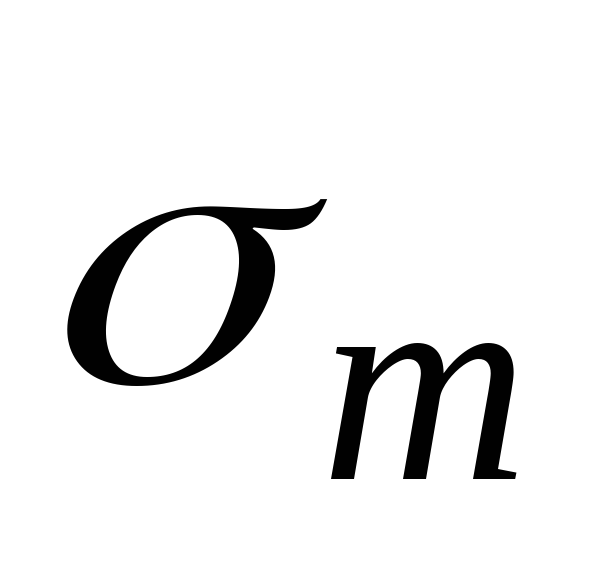 ввиду симметрии самой оболочки и нагрузки относительнго оси
ввиду симметрии самой оболочки и нагрузки относительнго оси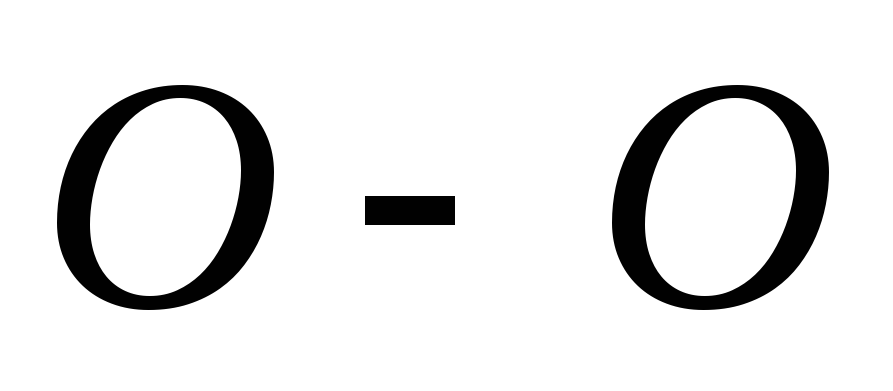 распределены по площади равномерно. Следовательно,
распределены по площади равномерно. Следовательно,
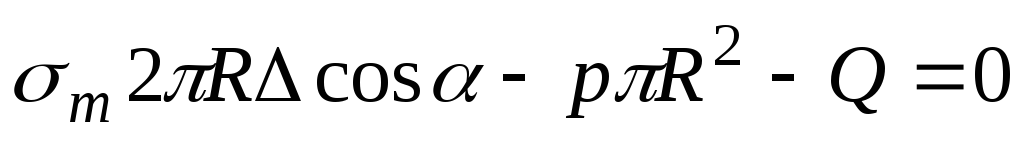 ,
,
откуда
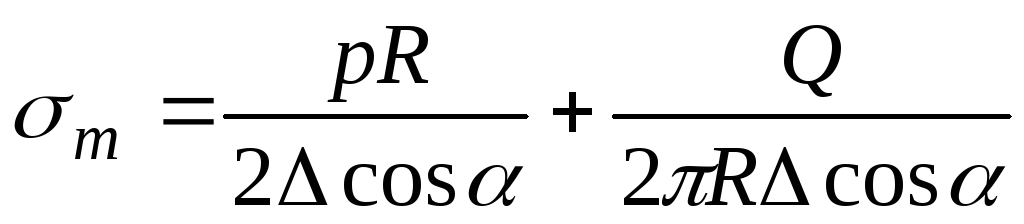 , (13.2)
, (13.2)
где  вес части сосуда и жидкости, лежащих ниже рассматриваемого сечения;
вес части сосуда и жидкости, лежащих ниже рассматриваемого сечения;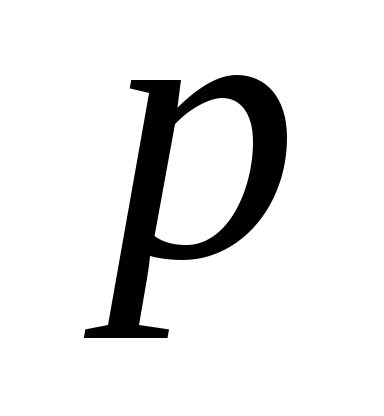 давление жидкости, по закону Паскаля одинаковое во всех направлениях и равное
давление жидкости, по закону Паскаля одинаковое во всех направлениях и равное , где
, где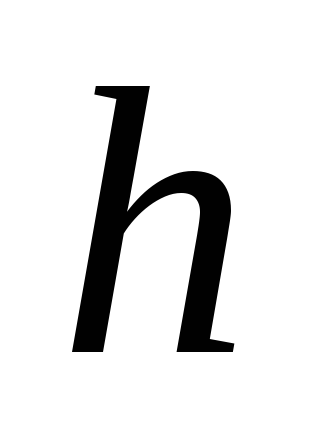 глубина рассматриваемого сечения, а
глубина рассматриваемого сечения, а вес единицы объема жидкости. Если жидкость хранится в сосуде под некоторым избыточным в сравнении с атмосферным давлением
вес единицы объема жидкости. Если жидкость хранится в сосуде под некоторым избыточным в сравнении с атмосферным давлением , то в этом случае
, то в этом случае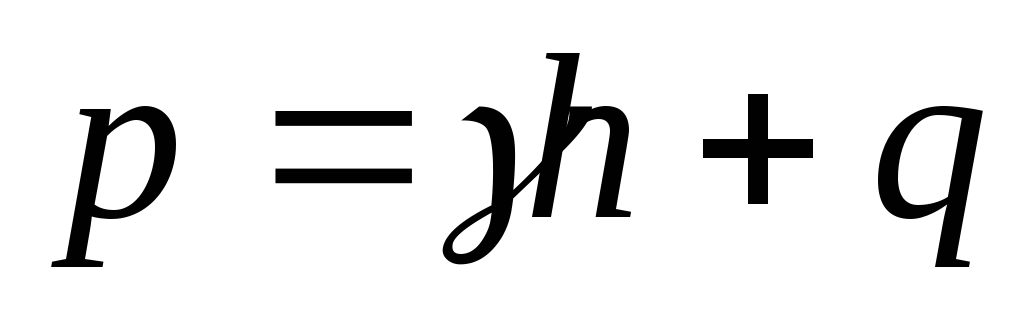 .
.
Теперь, зная напряжение 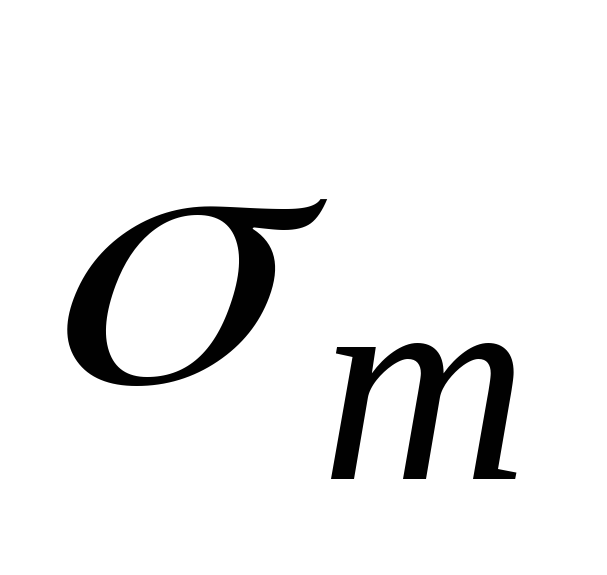 из уравнения Лапласа (13.1) можно найти напряжение
из уравнения Лапласа (13.1) можно найти напряжение .
.
При решении практических задач ввиду того, что оболочка тонкая, можно вместо радиусов срединной поверхности 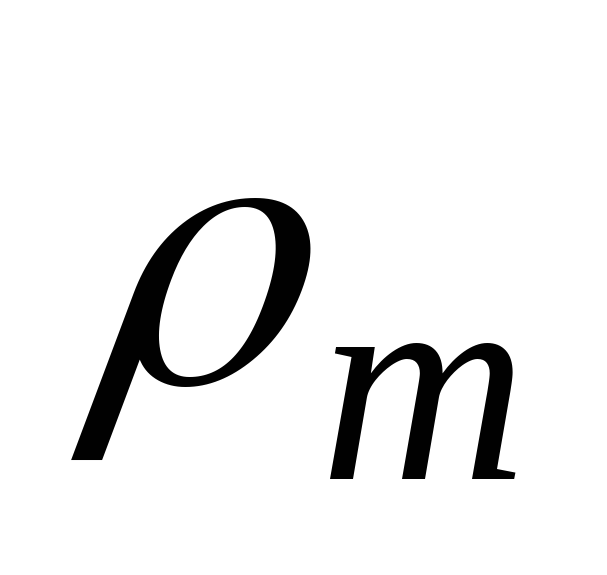 и
и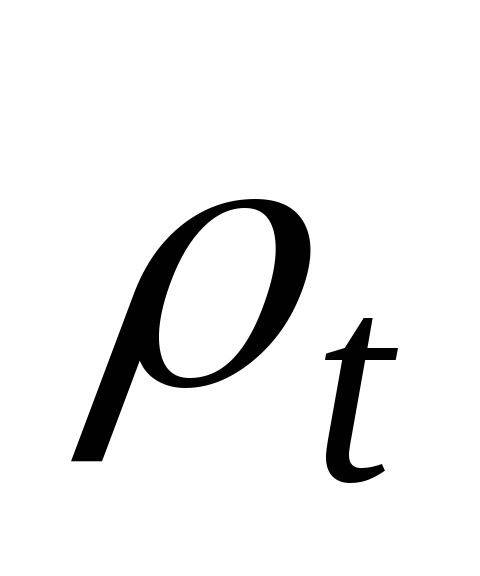 подставлять радиусы наружной и внутренней поверхностей.
подставлять радиусы наружной и внутренней поверхностей.
Как уже отмечалось окружные и меридиональные напряжения  и
и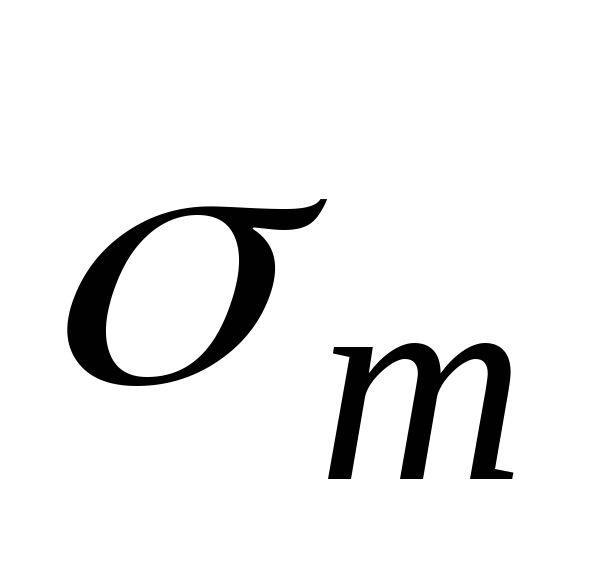 являются главными напряжениями. Что касается третьего главного напряжения, направление которого нормально к поверхности сосуда, то на одной из поверхностей оболочки (наружной или внутреннейв зависимости от того, с какой стороны действует давление на оболочку) оно равно
являются главными напряжениями. Что касается третьего главного напряжения, направление которого нормально к поверхности сосуда, то на одной из поверхностей оболочки (наружной или внутреннейв зависимости от того, с какой стороны действует давление на оболочку) оно равно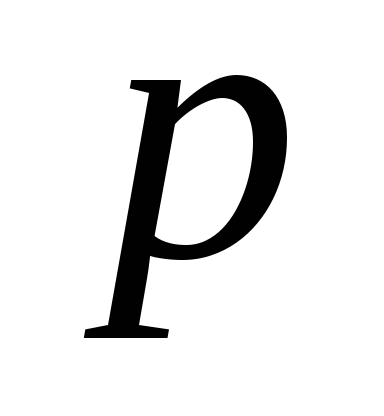 , а на противоположной – нулю. В тонкостенных оболочках напряжения
, а на противоположной – нулю. В тонкостенных оболочках напряжения и
и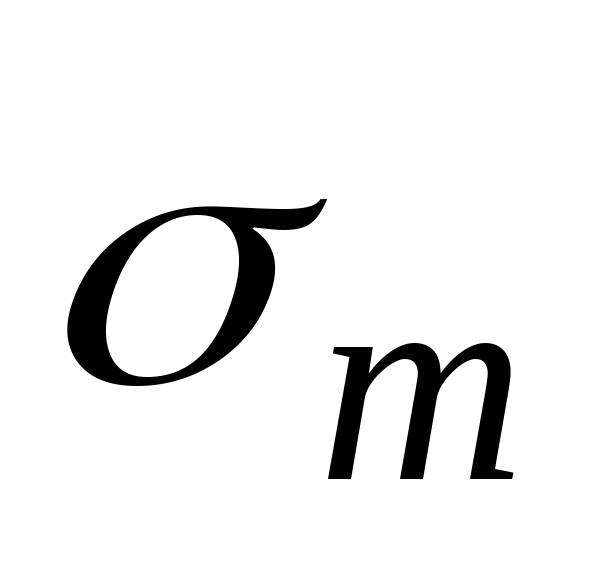 всегда значительно больше
всегда значительно больше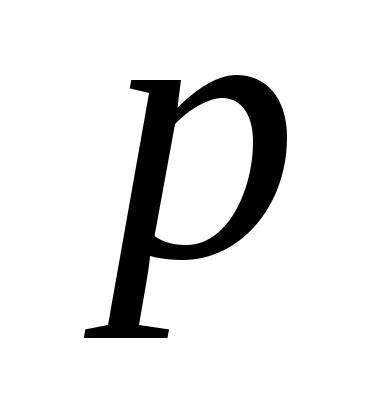 . Это означает, что величиной третьего главного напряжения можно пренебречь по сравнению с
. Это означает, что величиной третьего главного напряжения можно пренебречь по сравнению с и
и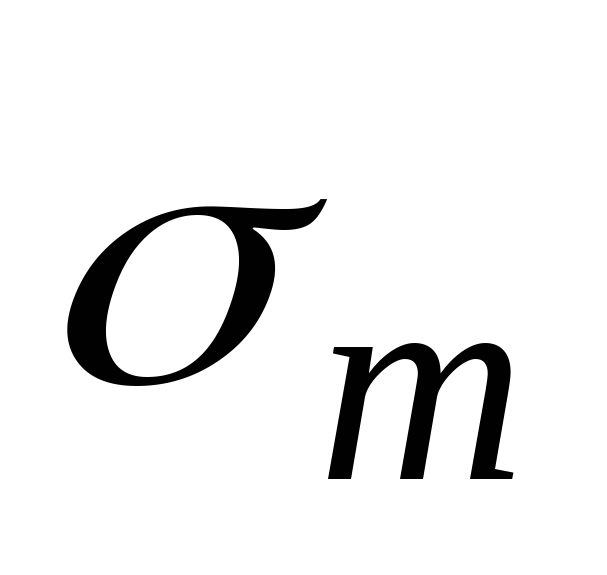 , т.е. считать его равным нулю.
, т.е. считать его равным нулю.
Таким образом, будем считать, что материал оболочки находится в плоском напряженном состоянии. В этом случае для оценки прочности в зависимости от состояния материала следует пользоваться соответствующей теорией прочности. Например, применив четвертую (энергетическую) теорию, условие прочности запишем в виде:
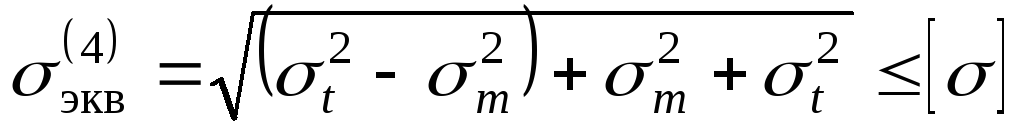 . (13.3)
. (13.3)
Рассмотрим несколько примеров расчета безмоментнтых оболочек.
Пример 13.1.Сферический сосуд находится под действием равномерного внутреннего давления газа (Рис.13.4). Определить напряжения действущие в стенке сосуда и оценить прочность сосуда с использованием третьей теории прочности. Собственным весом стенок сосуда и весом газа пренебрегаем.
(Рис.13.4). Определить напряжения действущие в стенке сосуда и оценить прочность сосуда с использованием третьей теории прочности. Собственным весом стенок сосуда и весом газа пренебрегаем.
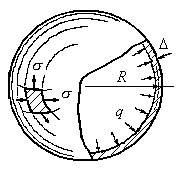
Рис.13.4
Решение:
1. Ввиду круговой симметрии оболочки и осесимметричности нагрузки напряжения  и
и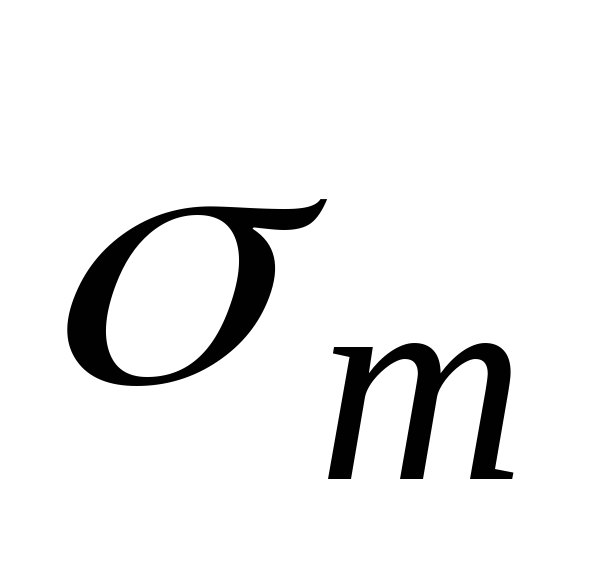 одинаковы во всех точках оболочки. Полагая в (13.1)
одинаковы во всех точках оболочки. Полагая в (13.1)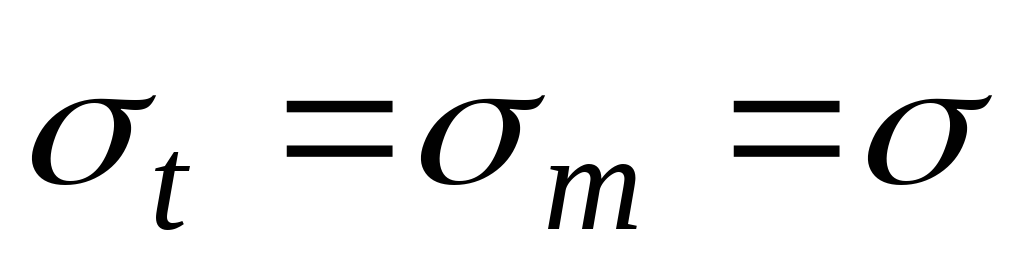 ,
,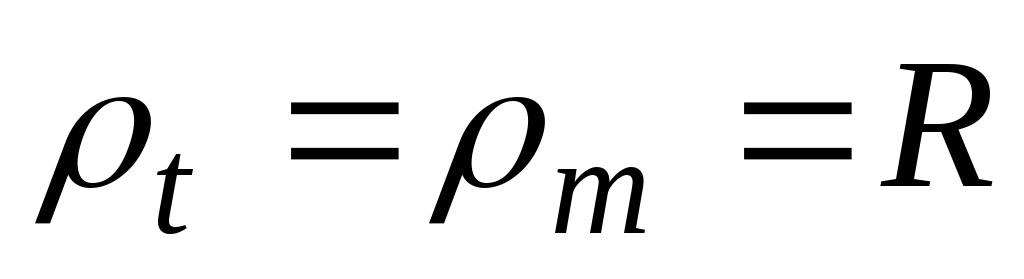 , а
, а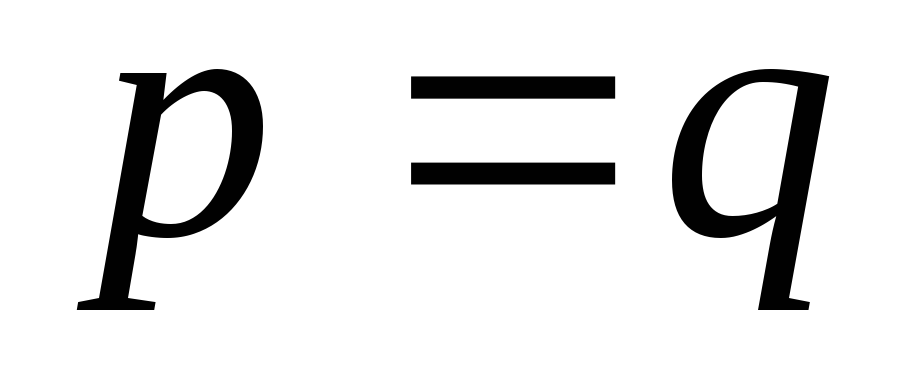 , получаем:
, получаем:
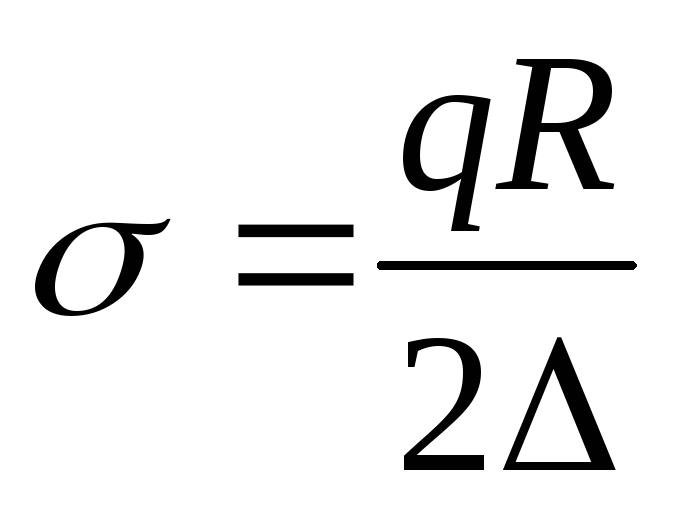 . (13.4)
. (13.4)
2. Выполняем проверку по третьей теории прочности:
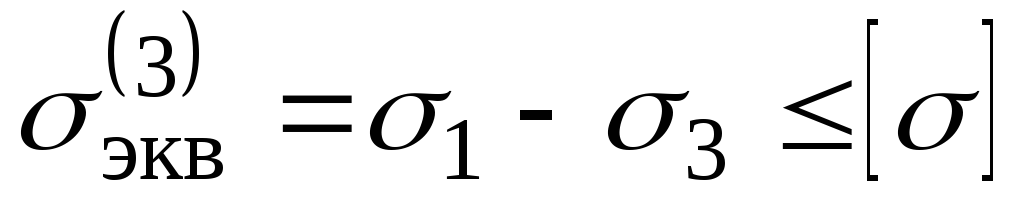 .
.
Учитывая, что 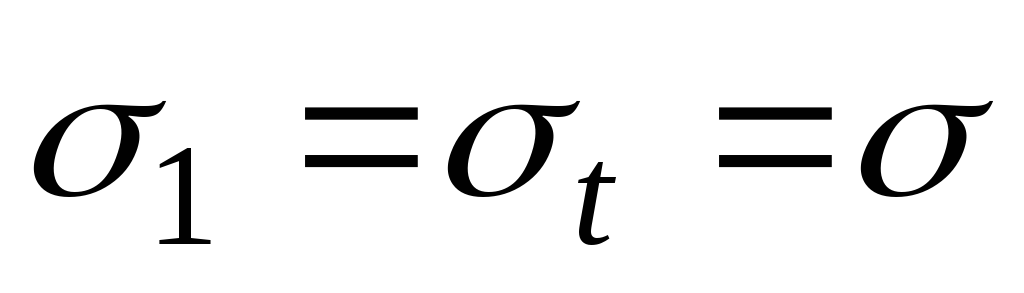 ,
,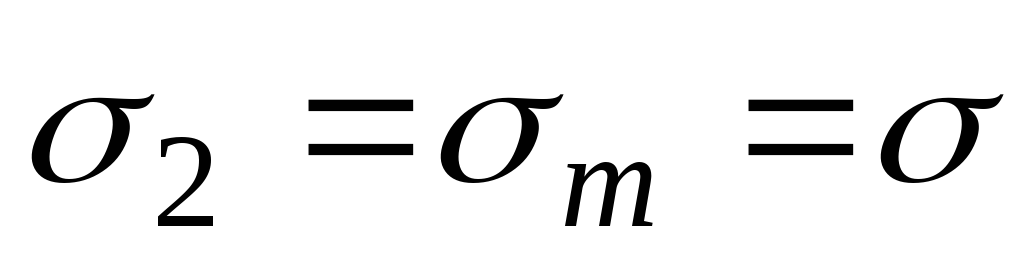 ,
,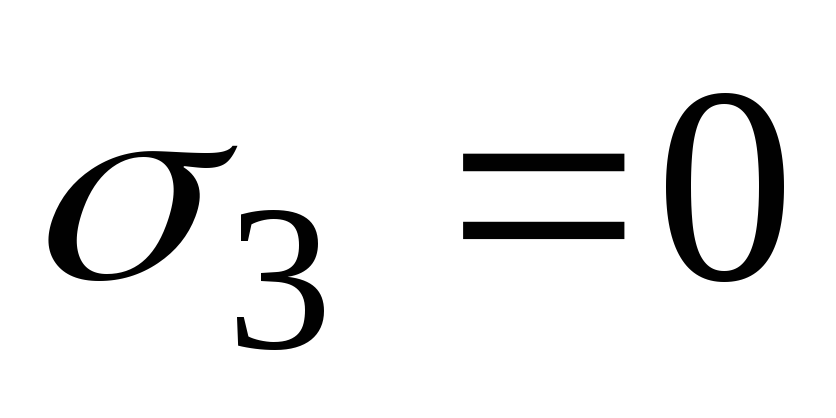 , условие прочности принимае вид:
, условие прочности принимае вид:
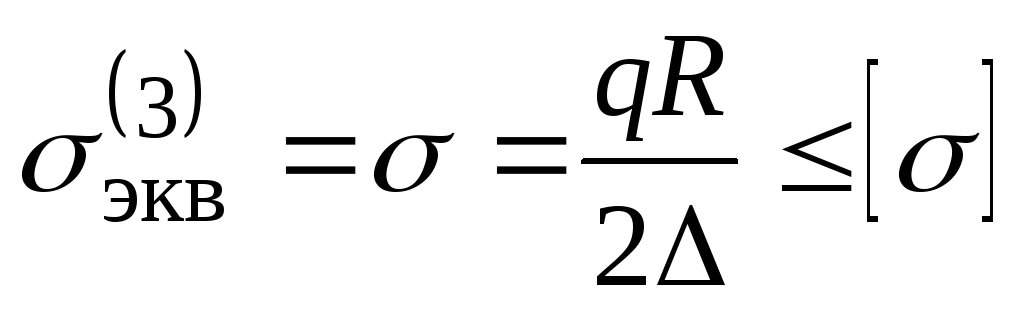 . (13.5)
. (13.5)
Пример 13.2.Цилиндрическая оболочка находится под действием равномерного внутреннего давления газа (Рис.13.5). Определить окружные и меридиональные напряжения, действующие в стенке сосуда, и оценить его прочность с использованием четвертой теории прочности. Собственным весом стенок сосуда и весом газа пренебречь.
(Рис.13.5). Определить окружные и меридиональные напряжения, действующие в стенке сосуда, и оценить его прочность с использованием четвертой теории прочности. Собственным весом стенок сосуда и весом газа пренебречь.
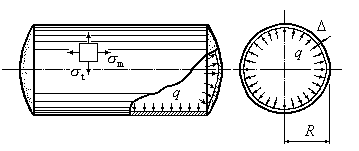
Рис.13.5
Решение:
1. Меридианами в цилиндрической части оболочки являются образующие, для которых 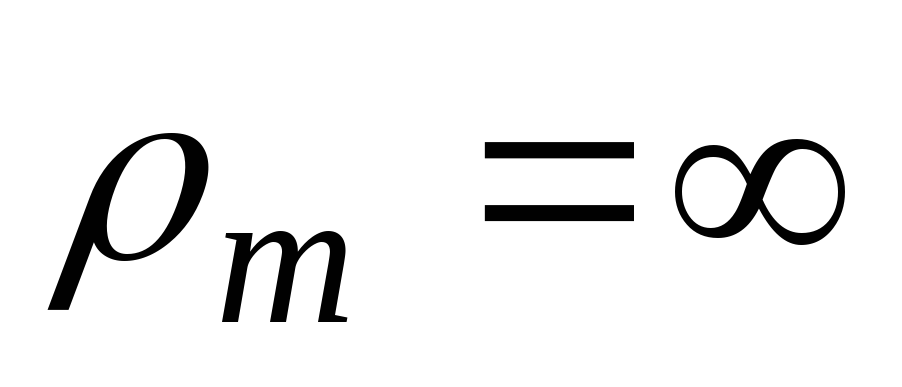 . Из уравнения Лапласа (13.1) находим окружное напряжение:
. Из уравнения Лапласа (13.1) находим окружное напряжение:
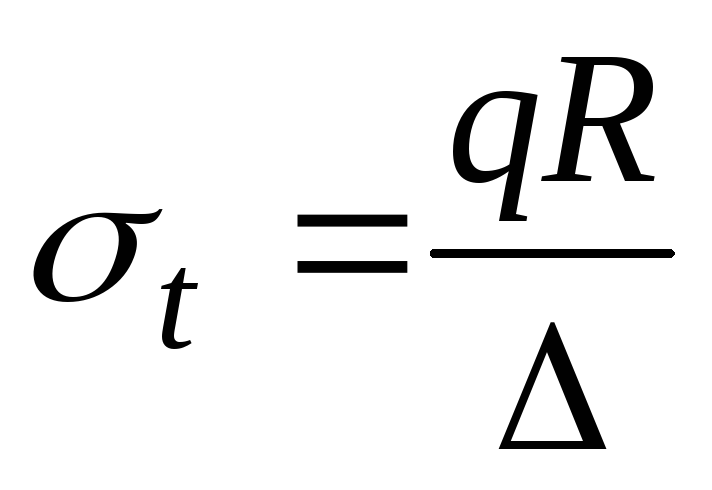 . (13.6)
. (13.6)
2. По формуле (13.2) находим меридиональное напряжение, полагая 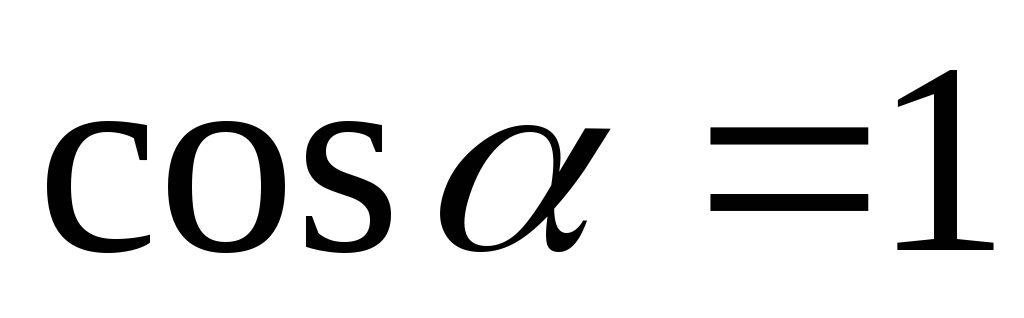 и
и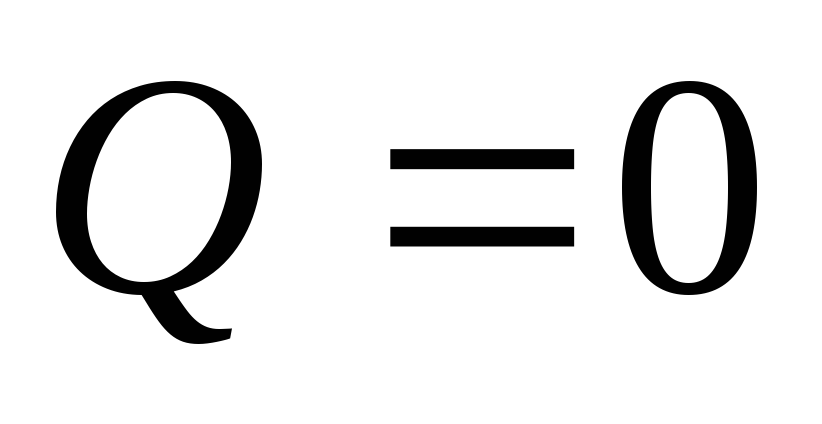 :
:
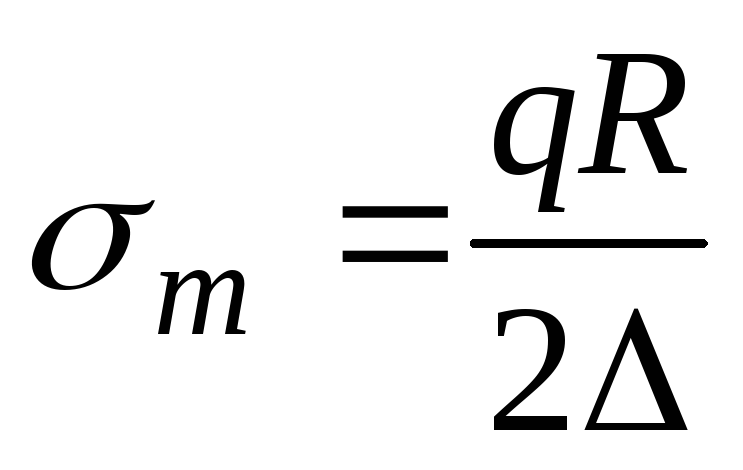 . (13.7)
. (13.7)
3. Для оценки прочности принимаем: 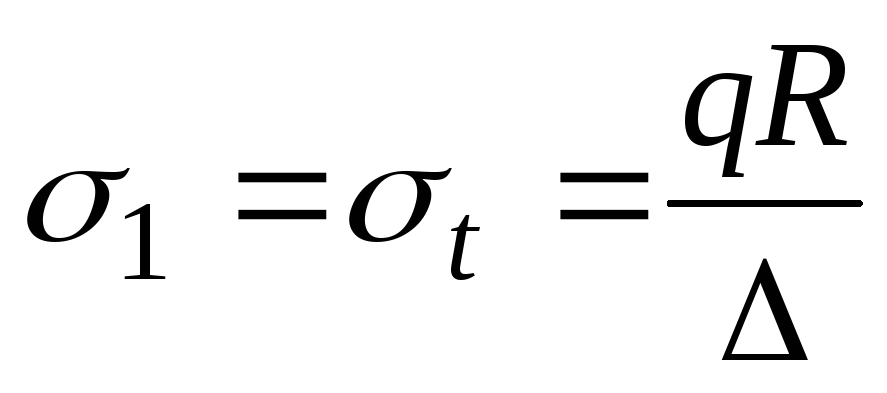 ;
;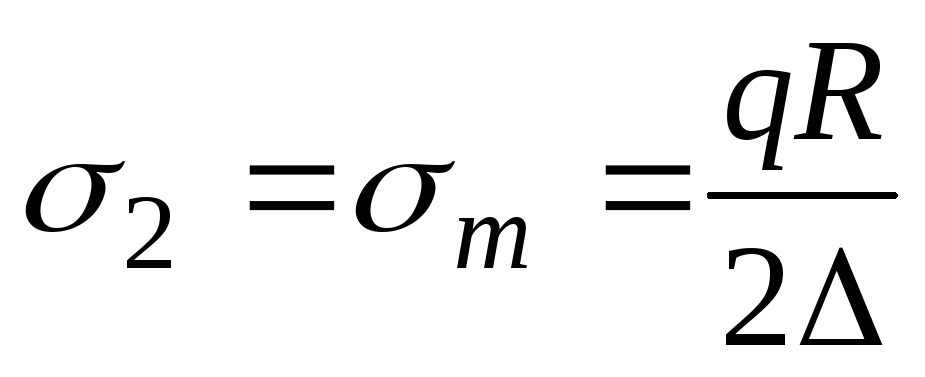 ;
;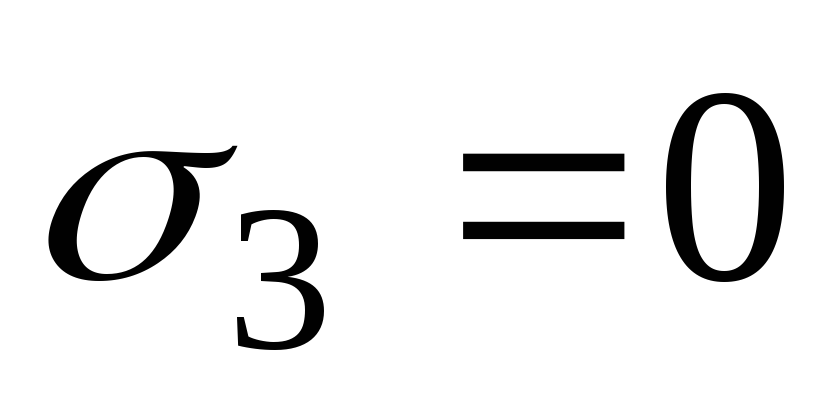 . Условие прочности по четвертой теории имеет вид (13.3). Подставляя в это условие выражения для окружных и меридиональных напряжений (а) и (б), получаем
. Условие прочности по четвертой теории имеет вид (13.3). Подставляя в это условие выражения для окружных и меридиональных напряжений (а) и (б), получаем
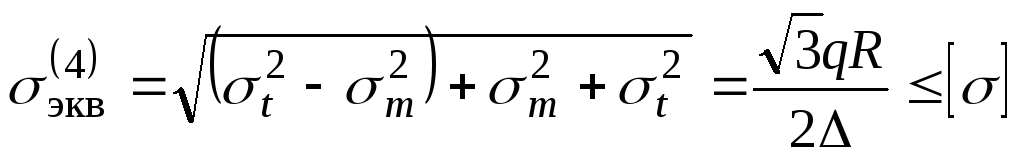 . (13.8)
. (13.8)
Пример 12.3.Цилиндрический резервуар с коническим днищем находится под действием веса жидкости (Рис.13.6,б). Установить законы изменения окружных и меридиональных напряжений в пределах конической и цилиндрической части резервуара, найти максимальные напряжения и
и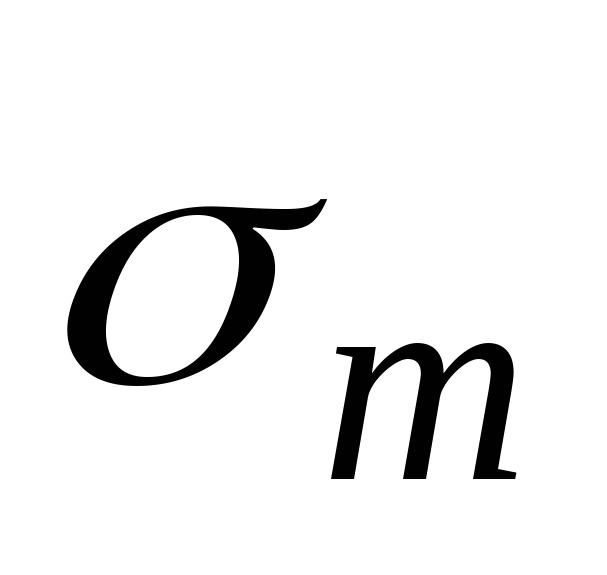 и построить эпюры распределения напряжений по высоте резервуара. Весом стенок резервуара пренебречь.
и построить эпюры распределения напряжений по высоте резервуара. Весом стенок резервуара пренебречь.
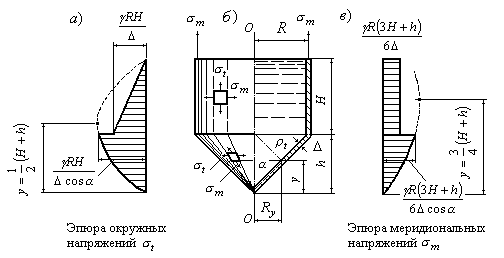
Рис.13.6
Решение:
1. Находим давление жидкости на глубине 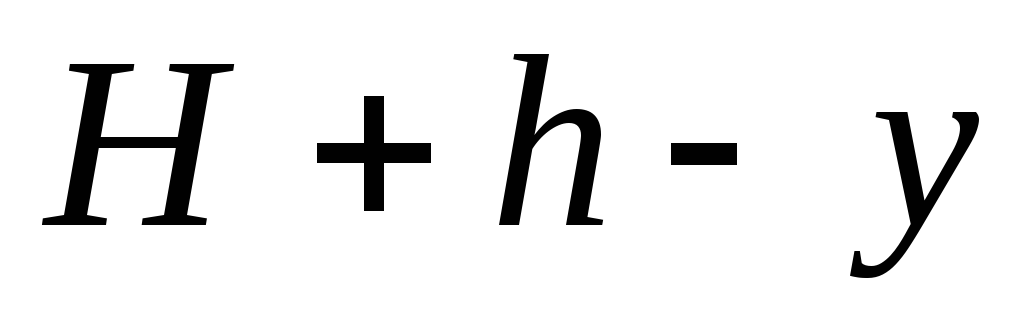 :
:
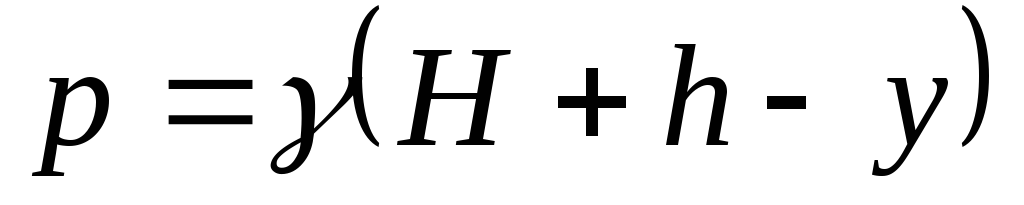 . (а)
. (а)
2. Определяем окружные напряжения из уравнения Лапласа, учитывая, что радиус кривизны меридианов (образующих) 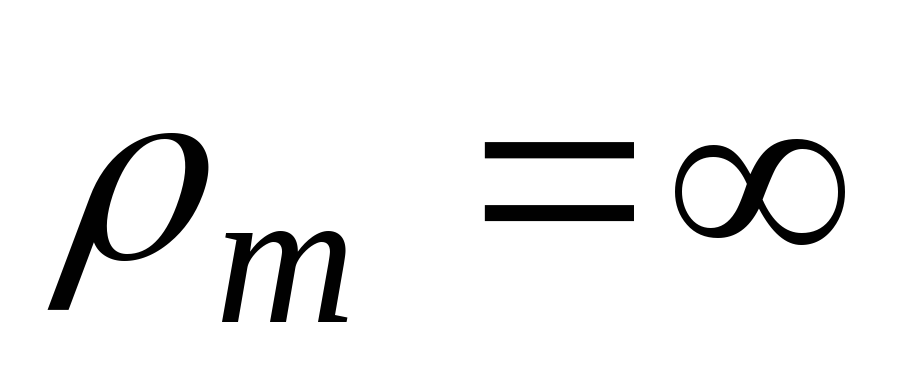 :
:
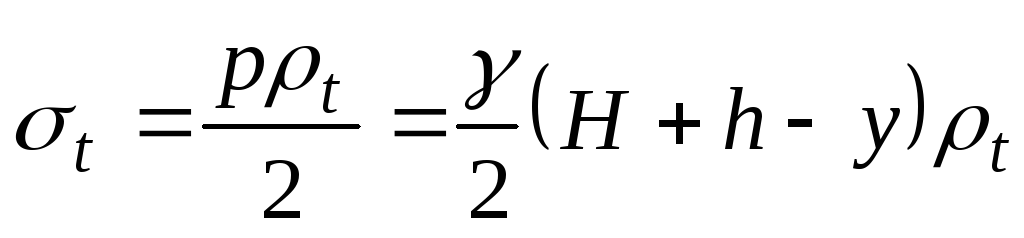 . (б)
. (б)
Для конической части оболочки
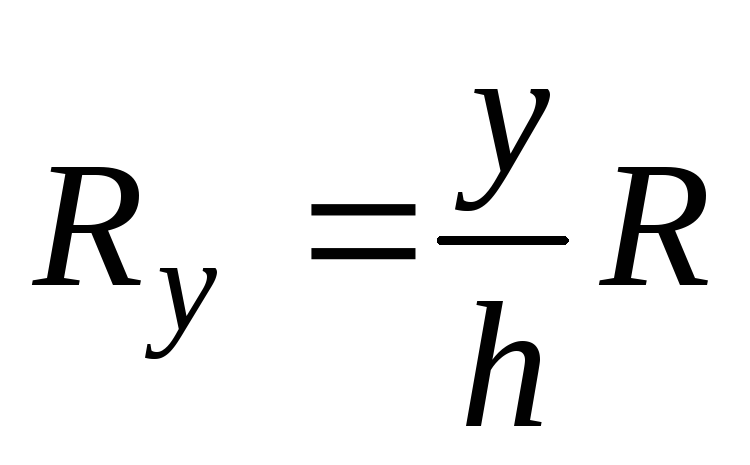 ;
;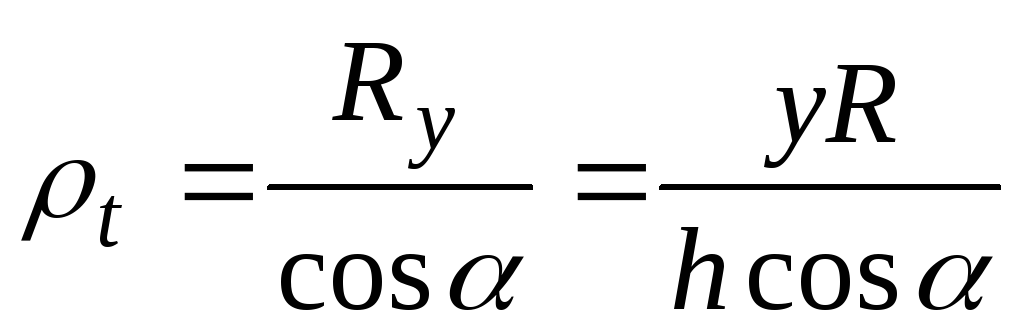 . (в)
. (в)
Подставляя (в) в (б) получим закон изменения окружных напряжений в пределах конической части резервуара:
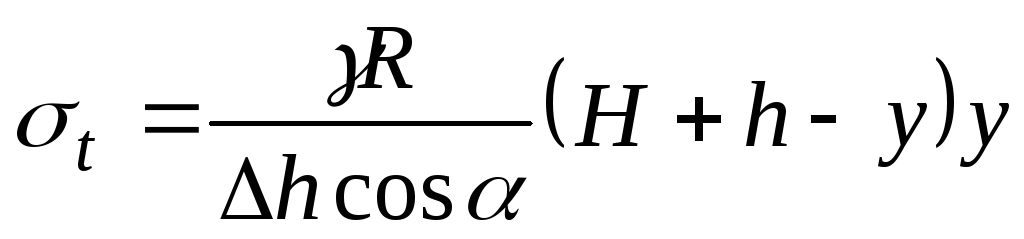 . (13.9)
. (13.9)
Для цилиндрической части, где 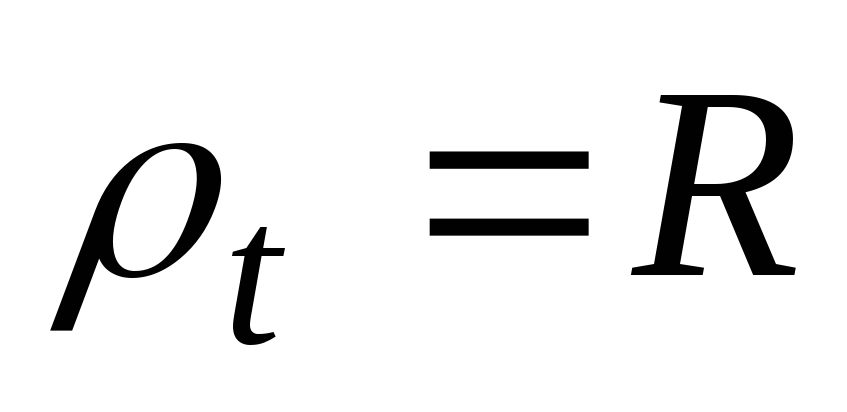 закон распределения окружных напряжений имеет вид:
закон распределения окружных напряжений имеет вид:
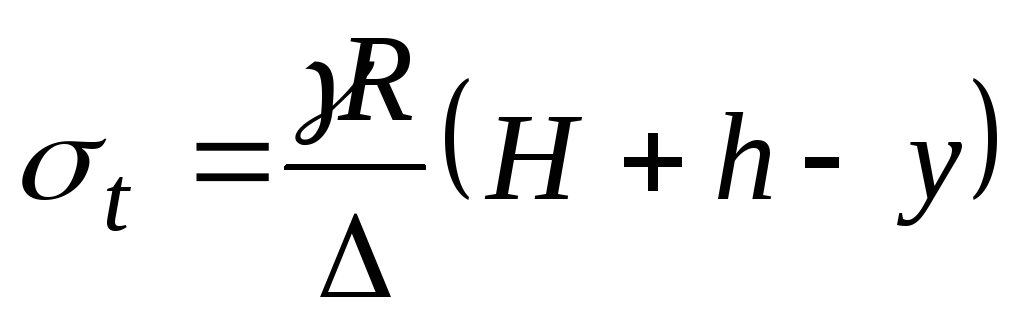 . (13.10)
. (13.10)

Эпюра  показана на рис.13.6,а. Для конической части эта эпюра параболическая. Ее математический максимум имеет место в середине общей высоты при
показана на рис.13.6,а. Для конической части эта эпюра параболическая. Ее математический максимум имеет место в середине общей высоты при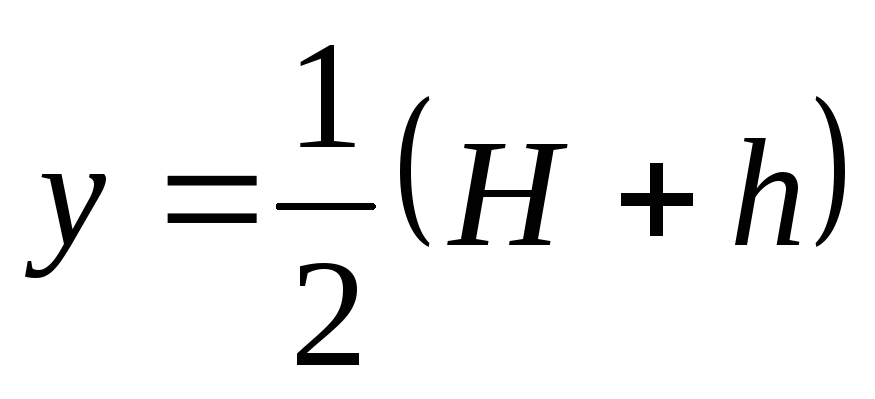 . При
. При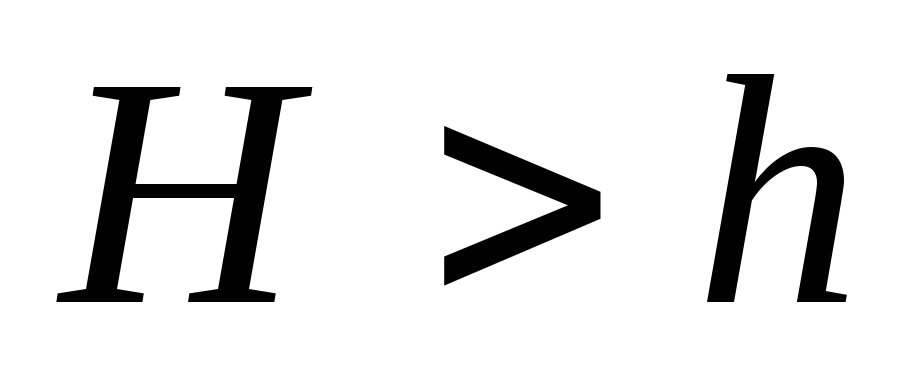 он имеет условное значение, при
он имеет условное значение, при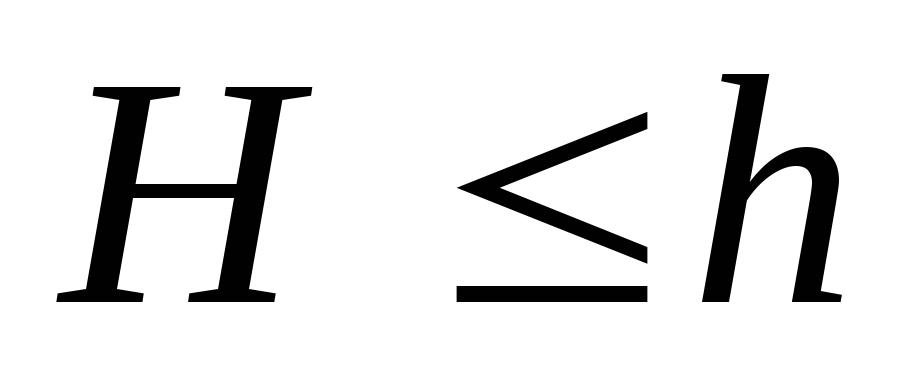 максимум напряжений попадает в пределы конической части и имеет реальное значение:
максимум напряжений попадает в пределы конической части и имеет реальное значение:
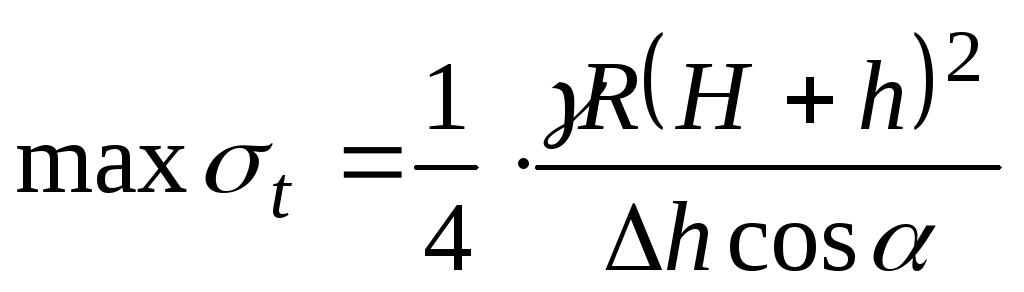 . (13.11)
. (13.11)
3. Определяем меридиональные напряжения 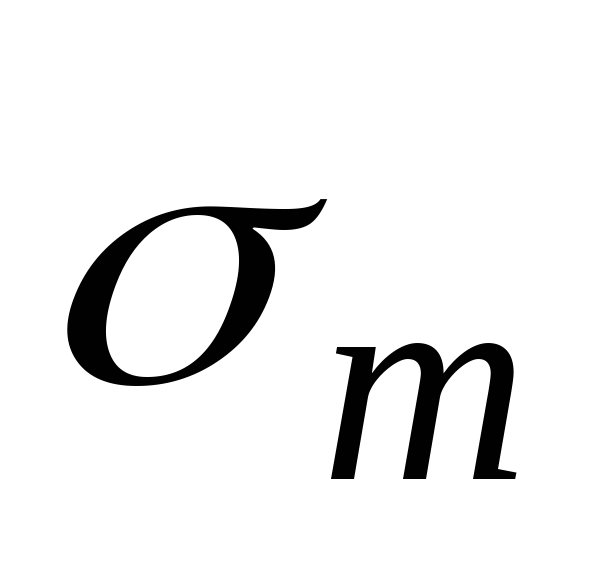 . Для конической части вес жидкости в объме конуса высотой
. Для конической части вес жидкости в объме конуса высотой равен:
равен:
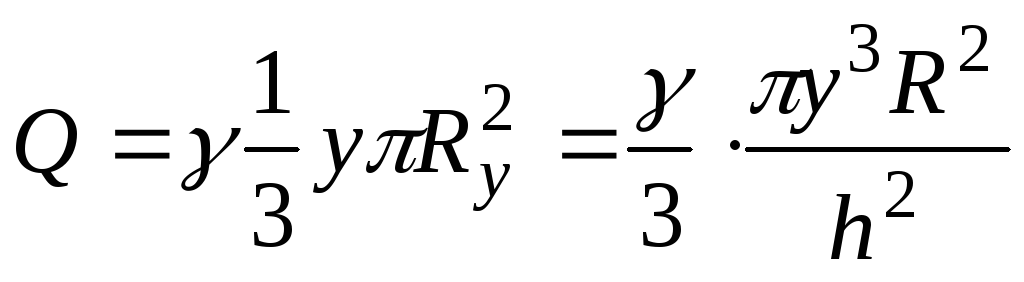 . (г)
. (г)
Подставляя (а), (в) и (г) в формулу для меридиональных напряжений (13.2) , получим:
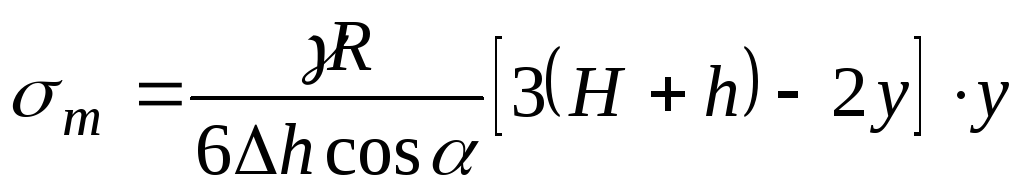 . (13.12)
. (13.12)
Эпюра 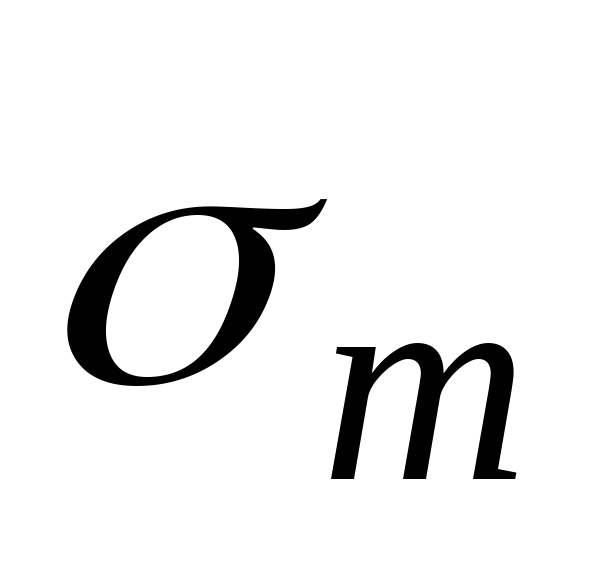 показана на рис.13.6,в. Максимум эпюры
показана на рис.13.6,в. Максимум эпюры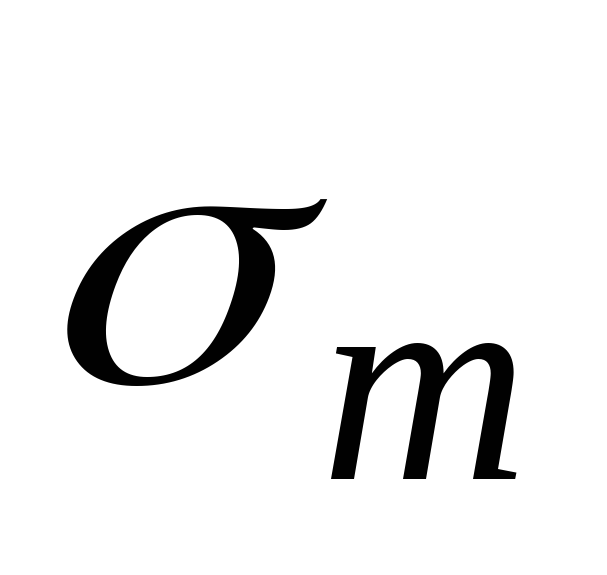 , очерченной для конической части также по параболе, имеет место при
, очерченной для конической части также по параболе, имеет место при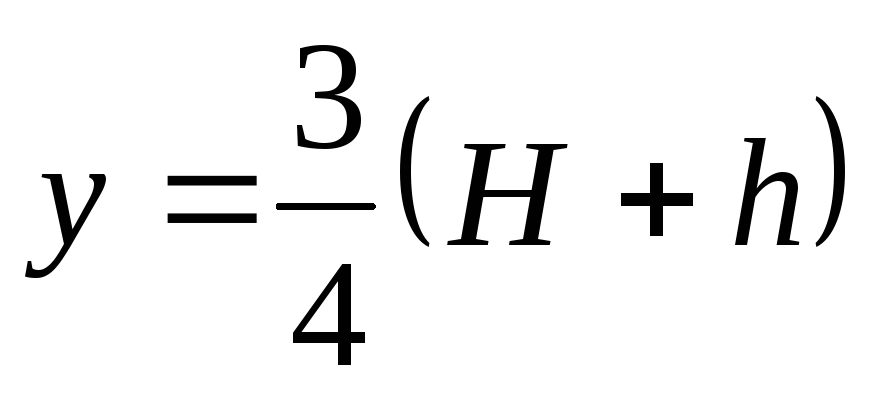 . Реальное значение он имеет при
. Реальное значение он имеет при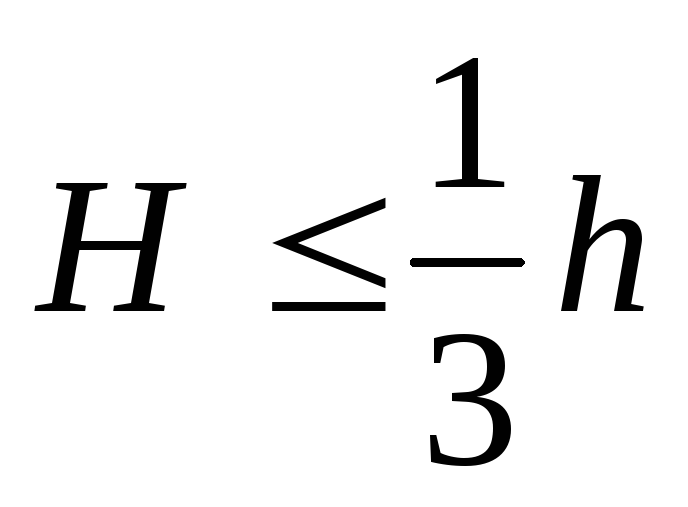 , когда попадает в пределы конической части. Максимальные меридиональные напряжения при этом равны:
, когда попадает в пределы конической части. Максимальные меридиональные напряжения при этом равны:
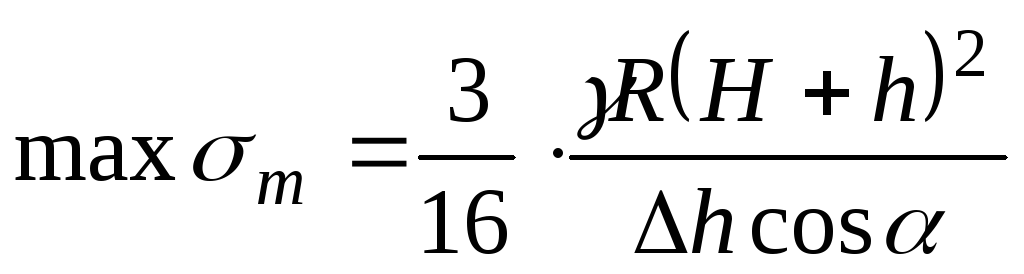 . (13.13)
. (13.13)
В цилиндрической части напряжение 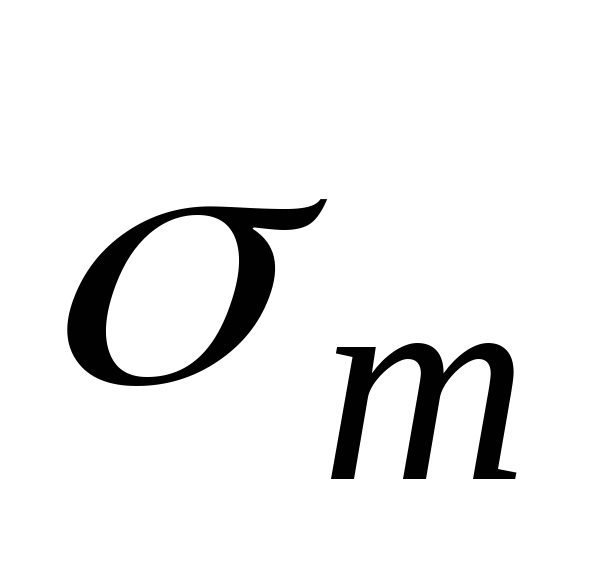 по высоте не меняется и равно напряжению у верхней кромки в месте подвеса резервуара:
по высоте не меняется и равно напряжению у верхней кромки в месте подвеса резервуара:
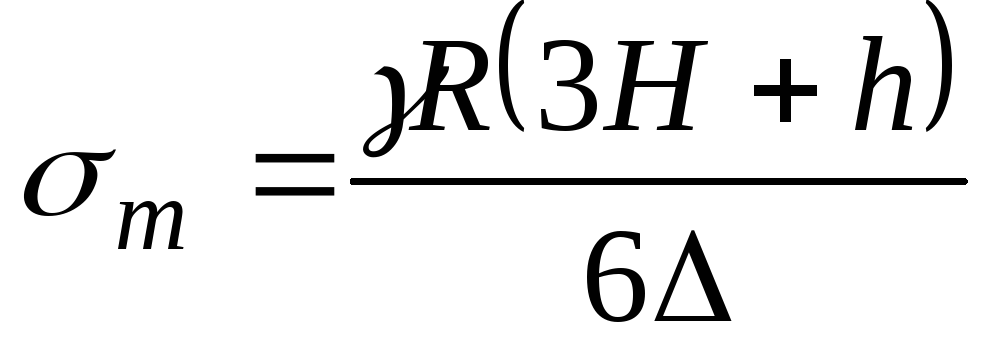 . (13.14)
. (13.14)
В местах, где поверхность резервуара имеет резкий излом, как, например, в месте перехода от цилиндрической части к конической (Рис.13.7) (Рис.13.5), радиальная составляющая меридиональных напряжений 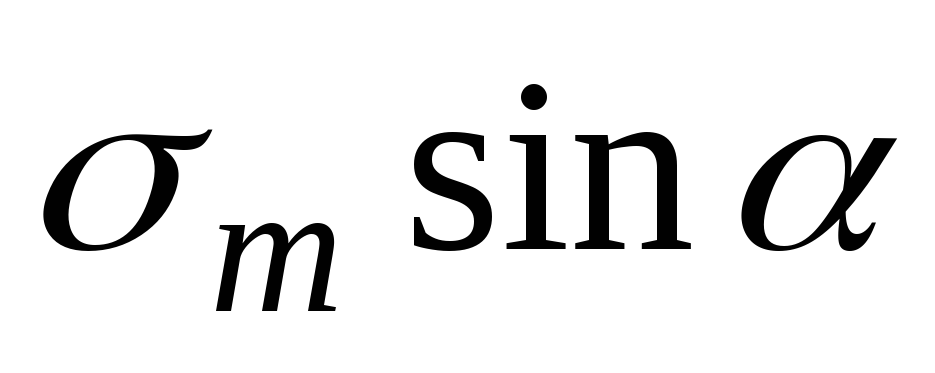 не уравновешена (Рис.13.7).
не уравновешена (Рис.13.7).
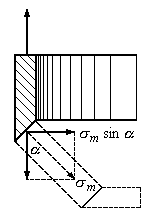
Рис.13.7
Эта составляющая по периметру кольца создает радиальную распределенную нагрузку интенсивностью 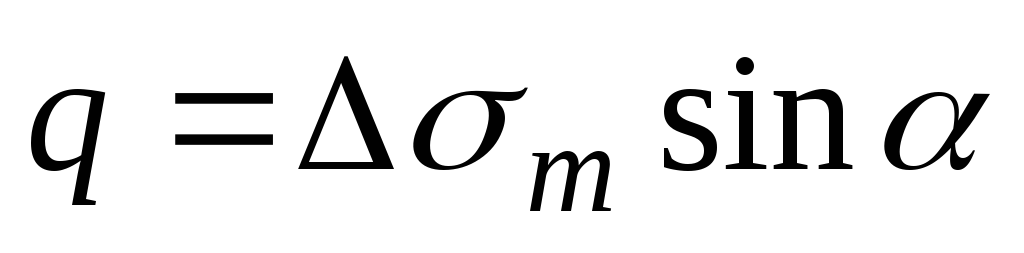 , стремящуюся согнуть кромки цилиндрической оболочки внутрь. Для устранения этого изгиба ставится ребро жесткости (распорное кольцо) в виде уголка или швеллера, опоясывающего оболочку в месте перелома. Это кольцо воспринимает радиальную нагрузку
, стремящуюся согнуть кромки цилиндрической оболочки внутрь. Для устранения этого изгиба ставится ребро жесткости (распорное кольцо) в виде уголка или швеллера, опоясывающего оболочку в месте перелома. Это кольцо воспринимает радиальную нагрузку (Рис.13.8,а).
(Рис.13.8,а).
Вырежем двумя бесконечно близко расположенными радиальными сечениями из распорного кольца его часть (Рис.13.8,б) и определим внутренние усилия, которые в нем возникают. В силу симметрии самого распорного кольца и нагрузки, распределенной по его контуру, поперечная сила и изгибающий момент в кольце не возникают. Остается только продольная сила 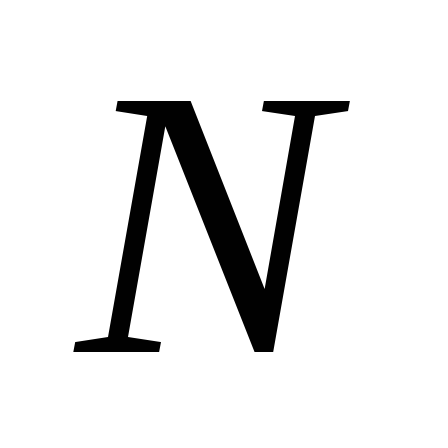 . Найдем ее.
. Найдем ее.
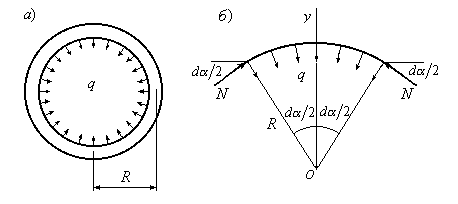
Рис.13.8
Составим сумму проекций всех сил, действующих на вырезанный элемент распорного кольца, на ось  :
:
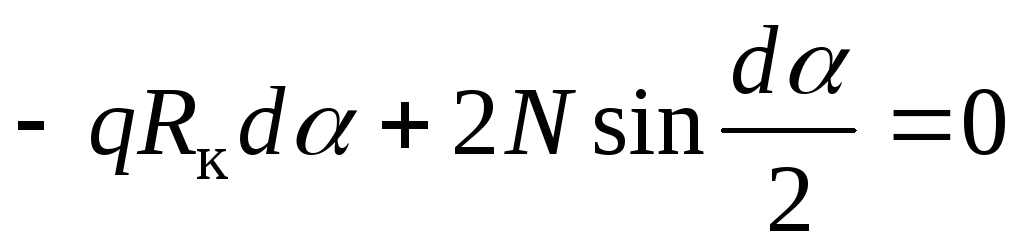 . (а)
. (а)
Заменим синус угла 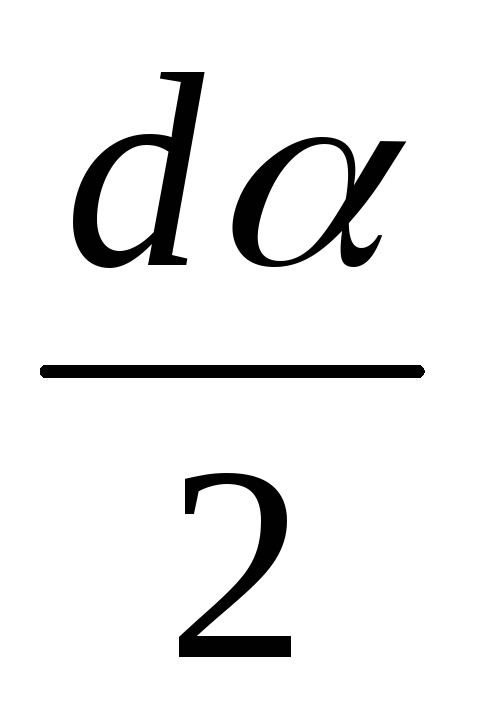 углом ввиду его малости
углом ввиду его малости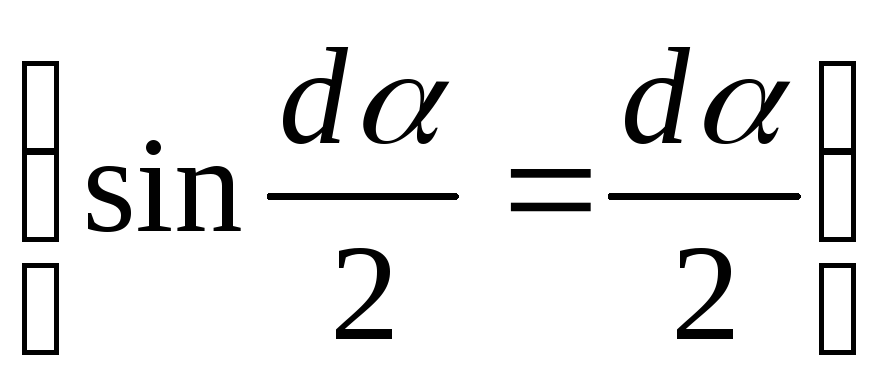 и подставим в (а). Получим:
и подставим в (а). Получим:
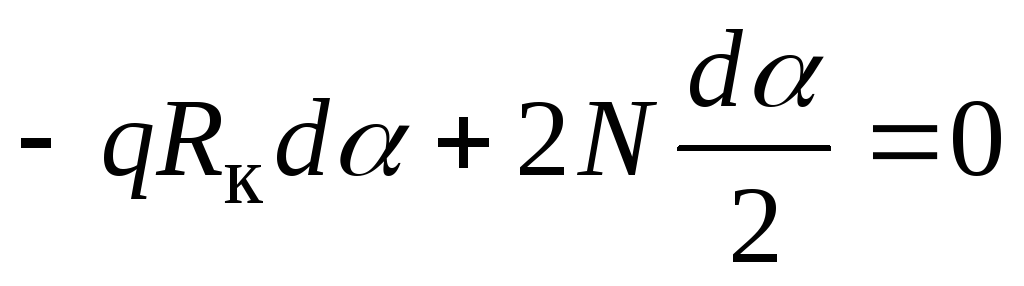 ,
,
откуда
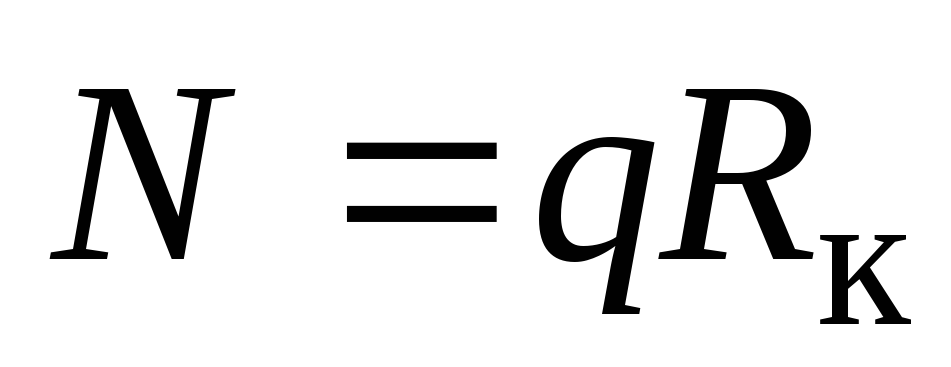 (13.15)
(13.15)
Таким образом, распорное кольцо работает на сжатие. Условие прочности принимает вид:
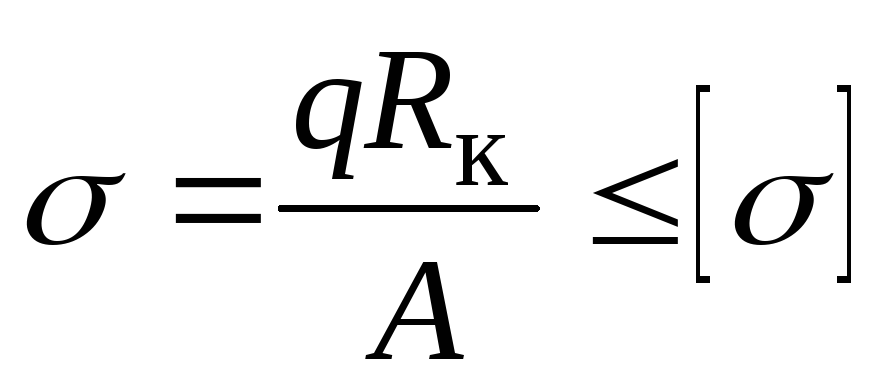 , (13.16)
, (13.16)
где 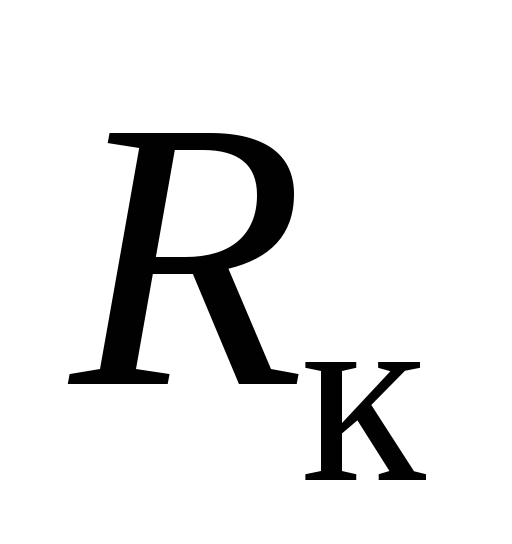 радиус срединной линии кольца;
радиус срединной линии кольца; площадь поперечного сечения кольца.
площадь поперечного сечения кольца.
Иногда вместо распорного кольца создают местное утолщение оболочки, загибая края днища резервуара внутрь обечайки.
Если оболочка испытывает внешнее давление, то меридиональные напряжения будут сжимающими и радиальное усилие  станет отрицательным, т.е. направленным наружу. Тогда кольцо жесткости будет работать не на сжатие, а на растяжение. При этом условие прочности (13.16) останется таким же.
станет отрицательным, т.е. направленным наружу. Тогда кольцо жесткости будет работать не на сжатие, а на растяжение. При этом условие прочности (13.16) останется таким же.
Следует отметить, что постановка кольца жесткости полностью не устраняет изгиба стенок оболочки, так как кольцо жесткости стесняет расширение колец оболочки, примыкающих к ребру. В результате образующие оболочки вблизи кольца жесткости искривляются. Явление это носит название краевого эффекта. Оно может привести к значительному местному возрастанию напряжений в стенке оболочки. Общая теория учета краевого эффекта рассматривается в специальных курсах с помощью моментной теории расчета оболочек.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
