Расчет тонкостенных сосудов давления
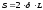
Если толщина стенок цилиндра мала по сравнению с радиусами и , то известное выражение для тангенцальных напряжений приобретает вид
т. е. величину, определенную нами раньше (§ 34).
Для тонкостенных резервуаров, имеющих форму поверхностей вращения и находящихся под внутренним давлением р, распределенным симметрично относительно оси вращения, можно вывести общую формулу для вычисления напряжений.
Выделим (Рис.1) из рассматриваемого резервуара элемент двумя смежными меридиональными сечениями и двумя сечениями, нормальными к меридиану.
Рис.1. Фрагмент тонкостенного резервуара и его напряженное состояние.
Размеры элемента по меридиану и по перпендикулярному к нему направлению обозначим соответственно и , радиусы кривизны меридиана и перпендикулярного к нему сечения обозначим и , толщину стенки назовем t.
По симметрии по граням выделенного элемента будут действовать только нормальные напряжения в меридиальном направления и в направлении, перпендикулярном к меридиану. Соответствующие усилия, приложенные к граням элемента, будут и . Так как тонкая оболочка сопротивляется только растяжению, подобно гибкой нити, то эти усилия будут направлены по касательной к меридиану и к сечению, нормальному к меридиану.
Усилия (Рис.2) дадут в нормальном к поверхности элемента направлении равнодействующую ab, равную
Рис.2. Равновесие элемента тонкостенного резервуара
Подобным же образом усилия дадут в том же направлении равнодействующую Сумма этих усилий уравновешивает нормальное давление, приложенное к элементу
Отсюда
Это основное уравнение, связывающее напряжения и для тонкостенных сосудов вращения, дано Лапласом.
Так как мы задались распределением (равномерным) напряжений по толщине стенки, то задача статически определима; второе уравнение равновесия получится, если мы рассмотрим равновесие нижней, отрезанной каким-либо параллельным кругом, части резервуара.
Рассмотрим случай гидростатической нагрузки (рис.3). Меридиональную кривую отнесем к осям х и у с началом координат в вершине кривой. Сечение проведем на уровне у от точки О. Радиус соответствующего параллельного круга будет х.
Рис.3. Равновесие нижнего фрагмента тонкостенного резервуара.
Каждая пара усилий , действующих на диаметрально противоположные элементы проведенного сечения, дает вертикальную равнодействующую bс, равную
сумма этих усилий, действующих по всей окружности проведенного сечения, будет равна ; она будет уравновешивать давление жидкости на этом уровне плюс вес жидкости в отрезанной части сосуда .
Отсюда
Зная уравнение меридиональной кривой, можно найти , х и для каждого значения у, и стало быть, найти , а из уравнения Лапласа и
Например, для конического резервуара с углом при вершине , наполненного жидкостью с объемным весом у на высоту h, будем иметь:
тогда
Для сферического сосуда радиусом , находящегося под внутренним давлением , по симметрии ; тогда из уравнения (Лапласа), так как
и
Если меридиональная кривая будет иметь переломы с разрывом непрерывности угла , то равновесие тонкой оболочки у места перелома может быть обеспечено лишь наличием реакций, приложенных к оболочке по окружности в этом месте. Появление таких реакций обеспечивается устройством специальных колец, способных брать на себя усилия, возникающие в них в связи с неуравновешенностью напряжений по обе стороны точки перелома.
Дальше…
Источник
Содержание:
- Расчёт тонкостенных сосудов.
Расчёт тонкостенных сосудов.
- Расчет тонкостенных кораблей. Если толщина стенки цилиндра t=p-G2 меньше радиуса g*! И G2 получается из Формулы (32.10: То есть значение, ранее определенное нами (§ 34). Для тонкостенного резервуара с вращающейся плоскостью можно вывести общую формулу для расчета напряжений, когда он находится под
внутренним давлением Р, которое распределено симметрично относительно направления вращения. Вы также можете выбрать следующие варианты: 548) из рассматриваемого резервуара в двух соседних меридианных секциях и двух нормальных секциях
Фигура. Пятьсот сорок восемь К Меридиану, направление ДС^6Т ДСМ
Людмила Фирмаль
и Фигура. Пятьсот сорок девять fydSmi Размеры элементов вдоль меридиана и перпендикуляра к нему указывают dsm и dSf соответственно, а радиус кривизны меридиана и поперечное сечение перпендикуляра к нему указывают PT и pf, а толщина стенки указывает t. Согласно симметрии плоскости выбранного элемента,
будут действовать только нормальные напряжения в направлении, перпендикулярном меридиану и Меридиану. Поскольку тонкая оболочка сопротивляется растяжению, подобно гибким нитям, эти силы направляются по касательной к участкам, перпендикулярным меридианам и меридианам. Это позволяет контролировать работу
- устройства. 549) дают результирующую ab в нормальном направлении к поверхности элемента, которая равна ab=dftt=^tdsm t. Точно так же усилия ВМ дстт дают равноденствия в том же направлении — § 199] расчет тонкостенного корабля 617 GM DS ids m — * сумма этих сил уравновешивает нормальное напряжение, приложенное к элементу П ДСМ ДСТ=^м dstdsm ДСМ ДСТ. Вечера Пт И так оно и есть. УК Я м/_ _ P_Pm Пт (32.14) Это основное уравнение at и SG / напряжения для вращающегося тонкостенного сосуда дано
Лапласом. Поскольку мы даем распределение (равномерное) напряжений по толщине стенки, задача статически определима. Рассмотрим начало ко-кривой и случай ко-гидростатического меридионального сечения CRI-x и Y. сечение Pro-O от точки. Радиус параллельного круга Нагрузка (рис. 550). В результате мы видим вертикальную ось на уровне вершины и соответствующий x Каждая пара vm усилий dstt работает на противоположном, давая Rav-DST элементы были проведены поперечное сечение, вертикальная
сумма, ing S=2ab cos6=2am cos 6 cos 6, Suma Bettiah aussiello,, deyjstvuyuthikp
Людмила Фирмаль
ppoo провел 2nxam t cos0=Ph2P4-вот сумма DST. В Отре- Ru_=Р*|_ t2t cos0 ″ G » 2ttxz cos6 * (32.15)) Зная уравнения меридиональной кривой x, можно найти 0, x и Ru Для каждого значения y, и таким образом узнать из уравнений (32.14) и at. Например,, чениченко даллаа reiseservice SS жидкость с объемным весом от высоты вершины углового оборудования — / y, мы имеем: ПМ=со; х=г тг а; ру=^^x2U=tg2a г; г);0=а; ф т=п О С О=. J’t g0. Ведь 618 расчет толстостенных и тонкостенных контейнеров[ГЛ. xxhp Затем ^(ч-г) уг-га. Т^8tg8a|TV8t г^м2т потому что синий тг от Zcosa2t потому что 6/удара = — НЕТ. [K_1u1 2Z COSa L3J J’ = Пи? т^л (ч-г)г тг в ’Т т т потому
что В случае сферического контейнера внутреннего давления G0 P0, по симметрии C^=at-a; тогда из уравнения (32.14), из Pm-P/ — G0t Если меридиональная кривая имеет излом с разрывом под углом 0, то равновесие тонкой оболочки в месте излома создается с помощью специального кольцевого устройства, в котором появление такой реакции при наличии реакции, приложенной к оболочке по окружности в этой точке, можно предположить силами, возникающими в этой точке.
Смотрите также:
- Примеры решения задач по сопротивлению материалов: сопромату
Источник
Тонкостенные
цилиндрические сосуды, подверженные
внутреннему давлению, имеют весьма
широкое распространение в технике
(трубопроводы, котлы и различного рода
емкости, заполненные жидкостью или
газом). Основной задачей при расчетах
таких сосудов является определение
необходимой толщины их стенок.
Пусть имеется
горизонтальный трубопровод (рис. 17)
внутренним диаметром
,
заполненный жидкостью, находящейся под
избыточным давлением
(изменение давления по вертикали
незначительно, поэтому им пренебрегаем).
Под влиянием этого давления стенки
трубопровода испытывают действие
разрывающего усилия, стремящегося
разорвать трубопровод по его образующей.
Таким образом, стенки трубопровода
будут работать на растяжение.
Рис. 17. К определению
толщины стенок труб, воспринимающих
внутреннее давление жидкости
Составим для
участка трубопровода длиной
уравнение прочности
,
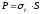(46)
где |
| – |
| – | |
| – |
. Так как поперечное
сечение трубы симметрично относительно
ее оси, достаточно рассмотреть разрывающее
усилие в какой-нибудь одной плоскости.
Разрывающее усилие, очевидно, представит
собой силу давления на полуцилиндрическую
поверхность и будет равно давлению на
проекцию этой поверхности на плоскость,
нормальную к направлению разрывающего
усилия, т.е.
.
Так как разрыв
стенок трубы возможен одновременно по
двум сечениям 1
– 1 и 2
– 2, площадь
сечения, по которому возможен разрыв
,
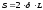где
– искомая толщина стенки трубы (сосуда).
Подставляя
полученные значения в исходное расчетное
уравнение, получим
,
откуда
.
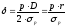(47)
Для вертикального
цилиндрического сосуда (резервуара)
диаметром
,
высотой
,
заполненного до краев жидкостью (рис.
18), разрывающее усилие определяется как
горизонтальная составляющая полного
давления на полуцилиндрическую
поверхность (равная давлению на проекцию
это поверхности на вертикальную
плоскость).
При этом изменением
давления по высоте пренебрегают и ведут
расчет по наибольшему давлению
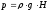у основания сосуда. Если же сосуд состоит
из ряда отдельных поясов, за расчетное
давление для каждого пояса принимают
давление у нижней его кромки.
Таким образом,
получаем
.
Рис. 18. Вертикальный
цилиндрический сосуд
Для определения
толщины стенок имеем условие
,
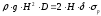откуда
.
(48)
Определим толщину
стенок сосуда из условия сопротивления
разрывающему усилию, направленному
вдоль оси сосуда (рис. 19). Разрывающее
усилие в этом случае определяется
произведением гидростатического
давления в в сосуде у его крышки или
днища на проекцию поверхности этой
крышки на плоскость, нормальную к оси
сосуда,
.
Рис. 19. Сосуд
воспринимающий разрывающее
усилие вдоль оси.
Сечение же, по
которому возможен отрыв крышки от
цилиндрической части сосуда, определяется
выражением
.
Следовательно
и толщина стенок
.
(49)
т.е.
получается в два раза меньше, чем в
первом случае.
Таким образом,
наиболее опасным с точки зрения прочности
является разрыв сосуда в продольном
направлении, и поэтому толщину стенок
следует определять по формуле (47);
выражение же (49) применяется при расчетах
поперечных швов.
Необходимо иметь
в виду, что полученные здесь зависимости
применимы без поправок лишь к расчетам
цельнотянутых или сварных сосудов. В
случае клепанных сосудов необходимо
учитывать неизбежное ослабление
материала склепываемых листов заклепочным
швом введением в расчетные формулы
коэффициента прочности заклепочного
шва
.
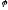Значение этого коэффициента устанавливается
в зависимости от типа заклепочного шва
и представляет собой отвлеченное число,
всегда меньшее единицы (
).
Кроме того, принимая во внимание
неизбежность коррозии и требования
технологии процесса клепки, получаемую
расчетом толщину стенок еще несколько
увеличивают на так называемый
производственный припуск
.
С учетом припуска
формулы (47) и (49) принимают вид
.
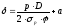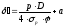
Для определения
результирующей силы
,
действующей в колене трубы рассмотрим
рис. 20.
,
(50)
Так как силы
направлены под углом α, то сила
.
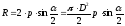(51)
Влиянием веса труб
в расчетах пренебрегаем.
Рис. 20. К определению
силы в колене трубы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Главная
Содержание
Расчет тонкостенных сосудов по безмоментной теории
Расчет толстостенных труб
Расчет тонкостенных сосудов по безмоментной теории
Задача 1.
Давление
воздуха в цилиндре амортизационной стойки шасси самолета в положении на стоянке
равно р=20 МПа. Диаметр цилиндра d=….. мм, толщина стенки
t=4
мм. Определить главные напряжения в цилиндре на стоянке и после взлета, когда
давление в амортизаторе ………………….
Ответ:
(на стоянке); (после взлета).
Задача 2.
Вода
поступает в водяную турбину по трубопроводу, наружный диаметр которого у
машинного здания равен …. м, а толщина стенки t=25 мм. Машинное здание
расположена на 200 м ниже уровня озера, из которого забирается вода. Найти
наибольшее напряжение в……………………….
Ответ:
Задача 3.
Проверить
прочность стенки ……………………………диаметром ….. м, находящегося под рабочим давлением
р=1 МПа, если толщина стенки t=12 мм, [σ]=100 МПа. Применить IV гипотезу прочности.
Ответ:
Задача 4.
Котел
имеет диаметр цилиндрической части d=….
м и находится под рабочим давлением р=….. МПа. Подобрать толщину стенки котла
при допускаемом напряжении [σ]=100 МПа, используя III гипотезу прочности. Какая была бы
необходимая толщина при использовании IV
гипотезы прочности?
Ответ:
Задача 5.
Стальная
сферическая оболочка диаметром d=1
м и толщиной t=….
мм нагружена внутренним давлением р=4 МПа. Определить………………
напряжения и ……………….. диаметра.
Ответ:
мм.
Задача 6.
Цилиндрический
сосуд диаметром d=0,8
м имеет стенку толщиной t=…
мм. Определить величину допускаемого давления в сосуде, исходя из IV
гипотезы прочности, если [σ]=…… МПа.
Ответ:
[р]=1,5 МПа.
Задача 7.
Определить …………………………..материала цилиндрической оболочки, если при нагружении ее внутренним давлением деформации в направлении
датчиков составили
Ответ:
ν=0,25.
Задача 8.
Дюралюминиевая
труба толщиной мм
и внутренним диаметром мм усилена плотно надетой на нее стальной
рубашкой толщиной мм.
Найти предельное ………………………..для двухслойной трубы по пределу текучести и ………………
напряжение между слоями в этот момент, полагая Ест=200 ГПа, Ед=70 ГПа,
Ответ:
Задача 9.
Водовод
диаметром d=….
мм в период пуска имел толщину стенки t=8
мм. В процессе эксплуатации вследствие коррозии толщина местами………………………
Какой максимальный столб воды может выдержит трубопровод
при двукратным запасе прочности, если предел текучести материала трубы равен
Задача 10.
Газопровод
диаметром d=…….
мм и толщиной стенки t=8
мм пересекает водохранилище при максимальной………………………….., достигающей 60 м. В
процессе эксплуатации газ перекачивается под давлением р=2,2
МПа, а при строительстве подводного перехода давление в трубе отсутствует. Чему
равны наибольшие напряжения в трубопроводе и когда они возникают?
Задача 11.
Тонкостенный
цилиндрический сосуд имеет полусферические днища. Каково должно быть
соотношение между толщинами цилиндрической и сферической частей, чтобы в зоне перехода не возникло………………….?
Задача 12.
При
изготовлении железнодорожных цистерн их испытывают под давлением р=0,6 МПа. Определить …………………………в цилиндрической части и в
днище цистерны, принимая давление при испытаниях за
расчетное. Расчет вести по III
гипотезы прочности.
Задача 13.
Между
двумя концентрически расположенными бронзовыми
трубами протекает жидкость под давлением р=6 МПа.
Толщина наружной трубы равна При какой толщине внутренней трубы обеспечивается …………………….. обеих труб? Чему
равны при этом наибольшие напряжения?
Задача 14.
Определите
………………………… материала оболочки, если нагружении ее
внутренним давлением деформации в направлении датчиков составили
Задача 15.
Тонкостенный
сферический сосуд диаметром d=1
м и толщиной t=1
см находится под действием внутреннего давления и внешнего Каков ………………….. сосуда Пт,
если
Будет
ли правильным следующее решение:
Задача 16.
Тонкостенная
труба с заглушенными концами находится под действием внутреннего давления р и изгибающего момента М. Пользуясь III гипотезой прочности,
исследуйте …………………… напряжения от величины М при заданном р.
Задача 17.
На
какой глубине находятся точки с ………………….. меридиональными и окружными
напряжениями для приведенного справа конического сосуда? Определите величины
этих напряжений, полагая удельный вес продукта равен γ=…. кН/м3.
Задача 18.
Сосуд
подвергается давлению газа р=10 МПа. Найти……………………,
если [σ]=250
МПа.
Ответ:
t=30
мм.
Задача 19.
Вертикально
стоящий цилиндрический резервуар с полусферическим днищем доверху заполнен
водой. Толщина боковых стенок и днища t=2
мм. Определить ………………………. напряжения в цилиндрической и сферической частях конструкции.
Ответ:
Задача 20.
Резервуар
цилиндрической формы дополнен до глубины Н1=6
м жидкостью с удельным весом а поверх не – на толщину Н2=2 м –
водой. Определить ……………………..резервуара у дна, если [σ]=60 МПа.
Ответ:
t=5
мм.
Задача 21.
Небольшой
газгольдер для светильного газа имеет толщину стенок t=5 мм. Найти ………………………………… верхнего и
нижнего сосудов.
Ответ:
Задача 22.
Поплавок
клапана испытательной машины представляет собой замкнутый цилиндр из
алюминиевого сплава диаметром d=…..
мм. Поплавок подвергается ………………………давлением р=23 МПа.
Определить толщину стенки поплавка, используя четвертую гипотезу прочности,
если [σ]=200 МПа.
Ответ:
t=5
мм.
Задача 23.
Тонкостенный
сферический сосуд с диаметром d=1
м и толщиной t=1
см находится под действием внутреннего ……………… и внешнего Каков ……………….. стенок сосуда если
Ответ:
.
Задача 24.
Определить
наибольшие ………………… и окружные напряжения в торообразном баллоне, если р=…. МПа,
t=3
мм, а=0,5 мм; d=0,4 м.
Ответ:
Задача 25.
Стальной
полусферический сосуд радиуса R=…
м заполнен жидкостью с удельным весом γ=7,5 кН/м3. Принимая …………………….
2 мм и пользуясь III
гипотезой прочности, определить необходимую толщину стенки сосуда, если
[σ]=80 МПа.
Ответ:
t=3
мм.
Задача 26.
Определить,
…………………… находятся точки с наибольшими меридиональными и окружными напряжениями
и вычислить эти напряжения, если толщина стенки t=… мм, удельный вес жидкости γ=10
кН/м3.
Ответ:
на глубине 2 м; на глубине 4 м.
Задача 27.
Цилиндрический
сосуд с коническим днищем заполнен жидкостью с удельным весом γ=7 кН/м3.
Толщина стенок постоянна и равна t=…мм.
Определить ……………………………..и окружные напряжения.
Ответ:
Задача 28.
Цилиндрический
сосуд с полусферическим днищем заполнен жидкостью с удельным весом γ=10
кН/м3. Толщина стенок постоянна и равна t=… мм. Определить наибольшее напряжение в
стенке сосуда. Во сколько раз увеличится это напряжение, если длину………………………………,
сохранив неизменными все остальные размеры?
Ответ:
увеличится в 1,6 раза.
Задача 29.
Для
хранения нефти с удельным весом γ=9,5 кН/м3 используется сосуд
в виде усеченного конуса с толщиной стенки t=10 мм. Определить наибольшие ………………………….напряжения в стенке сосуда.
Ответ:
Задача 30.
Тонкостенный
конический колокол находится под слоем воды. Определить …………………………….. и
окружные напряжения, если давление воздуха на поверхность под колоколом толщина стенки t=10 мм.
Ответ:
Задача 31.
Оболочка
толщиной t=20
мм, имеющая форму эллипсоида вращения (Ох – ось вращения), нагружена внутренним
давлением р=…. МПа. Найти ………………….. в продольном и поперечном сечениях.
Ответ:
Задача 32.
Пользуясь
третьей гипотезой прочности, проверить прочность сосуда, имеющего форму
параболоида вращения с толщиной стенки t=… мм, если удельные вес жидкости
γ=10 кН/м3, допускаемое напряжение [σ]=20 МПа, d=h=5 м. Прочность
проверить по высоте……………………………
Ответ:
т.е. прочность обеспечена.
Задача 33.
Цилиндрический
сосуд со сферическими днищами предназначен для хранения газа под давлением р=… МПа. Под ………………… можно будет хранить газ в сферическом сосуде той же емкости при
неизменном материале и толщине стенки? Какая при этом достигается экономия
материала?
Ответ:
экономия составит 36%.
Задача 34.
Цилиндрическая
оболочка с толщиной стенки t=5
мм сжимается силой F=…..
кН. Образующие оболочки из-за неточности изготовления
получили малое…………………………. Пренебрегая влиянием этого искривления на
меридиональные напряжения, вычислить в середине высоты оболочки в предположении,
что образующие искривлены по одной полуволне синусоиды, а f=0,01l;
l=r.
Ответ:
Задача 35.
Вертикальный цилиндрический сосуд предназначен для хранения
жидкости объема V
и удельного веса γ. Суммарная толщина верхнего и нижнего оснований,
назначаемая по конструктивным соображениям, равна Определить наивыгоднейшую высоту резервуара Нопт,
при которой масса конструкции будет минимальна.
Принимая высоту резервуара, равной Нопт,
найти ………………………….. части, полагая [σ]=180 МПа, Δ=9 мм, γ=10 кН/м3,
V=1000
м3.
Ответ:
Нопт=9 м, мм.
Задача 36.
Длинная
тонкая трубка толщиной t=….
мм надета с натягом Δ на абсолютно жесткий стержень диаметра d=….. мм. …………… необходимо приложить к
трубке, чтобы снять ее со стержня, если Δ=0,0213 мм; f=0,1; l=10
см, Е=100 ГПа, ν=0,35.
Ответ:
F=10
кН.
Задача 37.
Тонкостенный
цилиндрический сосуд со сферическими днищами подвергается изнутри давлению газа
р=7 МПа. Путем ……………………………….. диаметром ,
уложенной виток к витку с начальным натяжением N02,
обеспечивается равнопрочность оболочки в окружном и
меридиональном направлениях. Определить толщину оболочки диаметр проволоки и начальное натяжение N02,
если Е1=Е2=200 ГПа.
Ответ:
N02=215
Н.
Задача 38.
Среди
прочих конструктивных элементов в авиационной и в ракетной технике используются
баллоны высокого давления. Обычно они имеют цилиндрическую или сферическую форму
и для них, как и для прочих конструктивных узлов, чрезвычайно важно соблюсти
требование минимального веса. Предлагается конструкция фасонного цилиндра,
показанная на рисунке. Стенки баллона состоят из нескольких цилиндрических
секций, связанных радиальными стенками. Поскольку цилиндрические стенки имеют
небольшой радиус, напряжения в них уменьшается, и можно надеяться, что несмотря на увеличение веса за счет радиальных стенок,
общий вес конструкции окажется меньшим, чем для обыкновенного цилиндра, имеющего
тот же объем …………………………….?
Задача 39.
Определить
……………………… тонкостенной оболочки равного сопротивления, содержащей жидкость
удельно веса γ.
Расчет толстостенных труб
Задача 1.
Какое
давление (внутреннее или наружное) ……………………. трубы? Во сколько раз наибольшие
эквивалентные напряжения по III гипотезе прочности в одном случае больше
или меньше, чем в другом, если величины давления одинаковы? Будут ли равны
наибольшие радиальные перемещения в обоих случаях?
Задача 2.
Две
трубы отличаются только размерами поперечного сечения: 1-я труба – а=20 см, b=30 см; 2-я труба – а=10 см, b=15
см. Какая из труб обладает ……………………… способностью?
Задача 3.
Толстостенная
труба с размерами а=20
см и b=40
см не выдерживает заданное давление. С целью повышения несущей способности
предлагаются два варианта: 1) увеличить в П раз
наружный радиус b;
2) уменьшить в П раз внутренний радиус а.
Какой из вариантов дает ……………………………. при одинаковом значении П?
Задача 4.
Труба
с размерами а=10
см и b=20
см выдерживает давление р=….. МПа. Насколько (в процентах) ……………….. несущая
способность трубы, если наружный радиус увеличить в …
раза?
Задача 5.
В
конце первой мировой войны (1918 г.) Германии была изготовлена
сверхдальнобойная пушка для обстрела Парижа с расстояния 115 км. Это была стальная труба 34 м длиной и толщиной стенок в казенной
части 40 см. Весило орудие 7,5 МН. Его 120-килограммовые снаряды имели метр в
длину при диаметре 21 см. Для заряда употреблялось 150 кг пороха, развивавшего
давление в 500 МПа, которое выбрасывало снаряд с начальной скоростью 2 км/с.
Каков должен быть……………………………., использованной для изготовления ствола орудия,
при не менее чем полуторакратным запасе прочности?
Задача 6.
Во
сколько раз …………………………….. толстостенного сосуда, если цельную трубу с
размерами, а=…. см
и b=40
см заменить составным цилиндром из двух соединенных с натягом труб? Посадка
труб выполнена по соотношению Гадолина?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин
Теория машин и механизмов
Источник