Распределение скоростей молекул газа в сосуде
Определение 1
С помощью закона распределения молекул по скоростям мы можем описать, как именно в макроскопической системе происходит распределение частиц (при условии ее нахождения в термодинамическом равновесии). Такое распределение называется стационарным, и воздействия внешних сил на систему при этом не происходит.
Данный закон распространяется как на жидкости, так и на газы, если на них действуют законы классической механики. Если мы знаем, как именно распределяются молекулы по своим скоростям, значит, мы можем ответить, какой объем молекул имеет определенную скорость в условиях заданной температуры в равновесном состоянии.
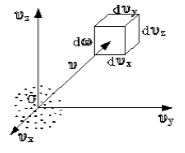
Чтобы лучше объяснить данный вопрос, начнем с введения такого понятия, как пространство скоростей. Оно изображено схематически на рисунке 1 .

Рисунок 1
Мы видим, что в декартовой системе координат здесь отмечены именно проекции скоростей, а не координаты. Тогда исходный вопрос можно переформулировать так: “Как именно будут распределяться молекулы в пространстве скоростей”?
Очевидно, что данное распределение не будет равномерным. Если в пространстве мы выделим параллелепипед, имеющий объем d ω = d υ x d υ y d υ z , то в нем окажется d N υ молекул. Обозначим буквой N число молекул газа, тогда f ( v ) будет некоторой функцией скорости.
Распределение Максвелла
Поскольку, как мы уже отмечали, газ находится в равновесном состоянии, то направления движений частиц являются равноправными. Значит, допустимо считать, что в пространстве скоростей распределение молекул является симметричным и имеет сферическую форму.
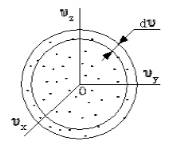
Рисунок 2
Определим, из скольких молекул состоит шаровой слой d υ . Разделим найденное выше число на количество частиц ( N ) и получим вероятность d W υ того, что пределы модуля скорости молекулы равны υ – υ + d v .
Здесь F ( v ) является функцией распределения вероятности значения v . Впервые данная функция теоретически была получена Д. Максвеллом.
Определение 2
Таким образом, закон распределения молекул по модулям скоростей имеет следующий вид:
d N υ = N 4 π m 0 2 πkT 3 2 e x p – m 0 υ 2 2 k T υ 2 d υ .
Здесь υ = υ x 2 + υ y 2 + υ z 2 , масса молекулы равна m 0 , а k – постоянная Больцмана.
По проекциям скоростей распределение Максвелла может быть записано так:
d N = N f υ x f υ y f υ z d υ x d υ y d υ z .
Важно учесть, что:
f υ i = m 0 2 πkT 1 2 e x p – m 0 υ i 2 2 k T ( i = x , y , z ) .
Параметры υ x , υ y , υ z означают проекции скоростей молекул на оси координат.
Также возможен следующий вариант записи распределения Максвелла:
d N = N 4 π υ v e r 3 e x p – υ υ v e r 2 υ 2 d υ .
Здесь υ υ e r обозначает наиболее вероятную скорость движения молекулы.
Как выглядит распределение Максвелла на графике
Кривая распределения молекул по скоростям на графике выглядит так:
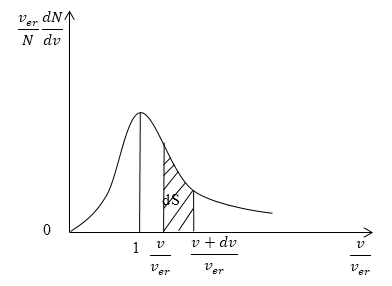
Рисунок 3
При этом доля тех молекул, которые движутся со скоростями в интервале от υ до υ + d υ будет пропорциональна площади d S , которая на графике обозначена штриховкой.
Определение 3
Скорости всех молекул принадлежат интервалу от нуля до плюс бесконечности, значит, будет верным равенство:
∫ 0 ∞ f ( υ ) d υ = 1 .
Оно называется условием нормировки функции распределения.
Следовательно, распределение Максвелла по скоростям имеет зависимость от температуры газа и массы его молекул. Объем и давление можно не учитывать.
Пример 1
Условие: вычислите, какова будет наиболее вероятная скорость молекул газа при температуре Т в равновесном состоянии.
Решение
Нам потребуется распределение Максвелла (распределение по модулям скоростей).
d N υ = N 4 π m 0 2 π k T 3 2 e x p – m 0 υ 2 2 k T υ 2 d υ .
Максимум функции будет соответствовать самой вероятной скорости. Дифференциация выражения по скорости и сравнение ее с нулем даст нам следующий результат:
d N υ d υ = N 4 π m 0 2 πkT 3 2 2 υ υ e r e x p – m 0 υ υ e r 2 2 k T – υ υ e r 2 m 0 2 υ υ e r 2 k T e x p – m 0 υ υ e r 2 2 k T = 0 ;
2 υ υ e r – υ υ e r 2 m 0 2 υ υ e r 2 k T = 0 → 1 – υ υ e r 2 m 0 2 k T = 0 → υ υ e r 2 = 2 k T m 0 .
υ υ e r = 2 k T m 0 .
Ответ: наиболее вероятно, что скорость газа будет равна υ υ e r = 2 k T m 0 .
Пример 2
Условие: изобразите кривые распределения скоростей молекул газа при росте температуры Т .
Решение
Возьмем формулу наиболее вероятной скорости из предыдущей задачи.
υ υ e r = 2 k T m 0
Понятно, что чем больше будет температура, тем выше будет скорость молекул, т.е. произойдет смещение максимума в сторону больших скоростей. Поскольку площадь под кривой распределения является постоянной величиной, кривые на графике будут показаны следующим образом:
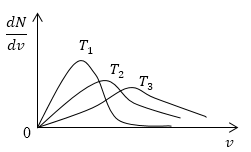
Рисунок 4
Пример 3
Условие: дан график функции, по которой молекулы будут распределяться с учетом проекций скорости υ x . Сопоставьте количества молекул, проекции скорости которых будут принадлежать интервалам от нуля до υ x 1 и от υ x 1 до υ x 2 .
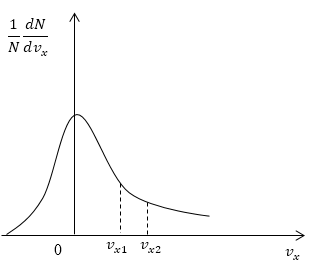
Рисунок 5
Решение
Как мы уже указывали ранее, доля молекул газа, скорости которых лежат в первом интервале, будет пропорциональна площади фигуры, образуемой кривой распределения, вертикальной осью 0 1 N d N d υ x и вертикальным пунктиром, перпендикулярным оси проекций. Во втором интервале нужная доля будет пропорциональна площади фигуры, ограниченной кривой распределения и вертикальной прямой, параллельной оси о х и проходящей через точку υ x 1 . Очевидно, что площадь первой фигуры будет меньше площади второй. Значит, и молекул, проекции скоростей которых лежат в первом интервале, будет меньше, чем во втором.
Ответ: молекул, имеющих проекции скорости в интервалах: от 0 до υ x 1 меньше, чем молекул, имеющих проекции скорости в интервалах: от υ x 1 до υ x 2 .
Источник
3.1. Распределение молекул между двумя половинками сосуда.
Применим теперь элементы теории вероятности для описания одноатомного идеального газа, заключенного в сосуд объемом . Рассмотрим сначала распределение молекул между двумя половинками сосуда.
Введем следующую терминологию:
Макросостояние – состояние, определяемое только известным количеством частиц в каждой из половин сосуда (без уточнения их номеров и, полагая частицы неразличимыми);
Микросостояние – состояние, определяемое нахождением конкретных (по номерам) частиц в каждой из половин сосуда (известно, частицы с какими номерами находятся в левой и правой половинах сосуда).
Статистический вес (статвес)- это число равновероятных микросостояний, посредством которых реализуется данное макросостояние.
1). Если имеется всего одна молекула, то вероятность найти ее в любой половине сосуда равна
(4.1).
2). Возьмем две молекулы, пронумеруем их и будем размещать их всеми возможными способами двум по половинкам сосуда. Очевидно, что всего возможны 4 (четыре) способа размещения:
Вероятность каждой из молекул оказаться в какой-либо половине сосуда равна . Поскольку положения молекул никак не зависят друг от друга, т.е. это независимые события, то, вероятность определенного размещения двух молекул сразу равна .
3). Пусть мы теперь имеем 4 молекулы. Пронумеруем эти частицы: 1, 2, 3, 4, считая, что это возможно сделать.
Итак, каждое “номерное” размещение частиц по половинкам сосуда – это микросостояние. Понятно, что
вероятность каждого микросостояния одинакова и в случае 4-х частиц равна: .
Построим таблицу:
| N | Макросостояние (число частиц в половинках сосуда) левая правая | Микросостояние (частицы с разными номерами в половинках сосуда) левая правая | Статистический вес (число микросостояний, соответствующих определенному макросостоянию) | Вероятность макросостояния |
| 0 4 | – 1,2,3,4 | 1/16 | ||
| 1 3 | 1 2,3,4 2 1,3,4 3 1,2,4 4 1,2,3 | 4 ×1/16 = 1/4 | ||
| 2 2 | 1,2 3,4 1,3 2,4 1,4 2,3 2,3 1,4 2,4 1,3 3,4 1,2 | 6 ×1/16 = 3/8 | ||
| 3 1 | 1,2,3 4 1,2,4 3 1,3,4 2 2,3,4 1 | 1/4 | ||
| 4 0 | 1,2,3,4 – | 1/16 |
Полная вероятность макросостояний равна, как и следует ожидать, единице:
.
Из данных таблицы видно, что наиболее вероятное макросостояние – это симметричное распределение молекул.
4). Рассмотрим, наконец, общий случай, когда в сосуде находится молекул.
Будем искать вероятность реализации макросостояния, при котором находятся: слева – частиц, справа- частиц. Выберем одно из микросостояний: слева – частицы с номерами ; справа – с номерами . Переставляя частицы местами, учтем, что макросостояние не изменяется (число частиц остается постоянным в каждой половинке сосуда), а микросостояние изменяется, если переставляются частицы из левой половины в правую, и не изменяется, если перестановки происходят только внутри каждой половины.
Сосчитаем статвес в рассматриваемого макросостояния. Полное число возможных перестановок в системе, содержащей частиц, равно . Чтобы получить число разных микросостояний в данном макросостоянии, исключим из них число перестановок внутри каждой половины, т.е., соответственно, и перестановок. Получаем, что статистический вес выбранного макросостояния равен числу сочетаний из по :
(3.2)
Очевидно, что вероятность каждого микросостояния равна
(3.3)
Тогда, вероятность рассматриваемого макросостояния ( молекул слева, а молекул справа) есть
. (3.4)
Из полученного выражения следует, что наиболее вероятным является макросостояние, соответствующее максимальному статистическому весу, который достигается при .
Пример: Пусть в сосуде находятся молекулы. Вероятность того, что все молекулы соберутся в одной половине сосуда, легко вычисляется:
статвес этого макросостояния и ,

т.е. вероятность такого события крайне мала уже при молекулах.
3.2. Распределение молекул в случае произвольных объемов.
Пусть в объеме находится молекул. Выделим в объеме меньший объем . Будем интересоваться макросостоянием, при котором в объеме находится частиц, а в остальной части объема содержится молекул. Вероятность того, что в объеме находится одна молекула находится равна отношению . Вероятность, что объем содержит две частицы: .
Если объем содержит частиц, то вероятность такого события – .
В то же время остальные молекул должны попасть в объем , вероятность чего равна
Т. о., вероятность реализации интересующего нас “микросостояния” (это условное микросостояние, т.к. клеточки пространства не одинаковы!):
(3.5)
Число способов такого распределения молекул газа в сосуде – это число соответствующих микросостояний, или статистический вес тот же, как в случае деления сосуда на равные половинки:
Итак, полная вероятность данного макросостояния записывается:
(3.6)
Итак, вероятность того, что в объеме будет обнаружено частиц из , определяется формулой (3.6).
Удобно ввести обозначения: , при этом .
Полученное распределение вероятностей называется биномиальным распределением:
. (3.7)
Биномиальное распределение (распределение Бернулли) – распределение вероятностей числа появлений некоторого события при повторных независимых испытания если вероятность появления этого события равна , .
Название распределения произошло от алгебраического бинома Ньютона:
. (3.8)
3.3. Свойства биномиального распределения.
1). Нормировка
Поскольку , то
, (3.9)
т.е. полная вероятность – вероятность обнаружения в малом объеме какого-либо числа частиц (от нуля до включительно) – нормирована на единицу.
2). Максимум вероятности.
Сразу же возникает резонный вопрос – какое из всех возможных состояний системы (макросостояний) будет реализовываться с максимальной вероятностью? Ясно, что вероятность состояния с очень малыми или при фиксированных и очень мала, т.к. при этом
или .
Т.е. максимум вероятности должен находиться при некоторых промежуточных значениях .
Вычисление максимума вероятности биномиального распределения.
Пусть нас интересуют достаточно большие и , такие что переход от вероятности к вероятности осуществляется непрерывным образом и – бесконечно малая величина. Чтобы найти максимум вероятности, вычислим разность вероятностей двух соседних состояний (при сделанных допущениях проведенная операция равносильна вычислению производной ) и приравняем ее нулю,:
(3.10)
Из равенства нулю выражения в скобках имеем
,
.
Т.к. и , получаем что
. (3.11)
Вспомним, что при ( , см. пункт 3.1), максимальная вероятность достигается тогда, когда максимален статвес , т.е. при равномерном распределении ( ) молекул газа по половинкам сосуда.
В общем случае, когда , как показывает расчет, максимум вероятности достигается при .
Из полученного результата вытекает исключительно важное следствие. Поскольку – концентрация молекул в объеме, то наиболее вероятным является состояние системы, когда число молекул в объеме равно , т.е. когда осуществляется равномерное заполнение (или распределение) молекулами всего объема сосуда.
Схематически картина распределения вероятности при достаточно больших значениях числах частиц и выглядит как показано на рисунке (дискретные точки соединены сплошной линией): в виде острого в пика окрестности c очень маленькой шириной . Условие нормировки может быть записано как
(3.12)
Если за газом наблюдать достаточно большое время, то окажется, что более вероятные распределения молекул возникают чаще, чем менее вероятные. Поэтому с течением времени газ именно и переходит в наиболее вероятные состояния, причем, достигнув наиболее вероятного состояния, газ в нем практически всегда и остается.
Такое состояние называется стационарным или равновесным.
Существенно, что равновесное состояние газа не зависит от предыстории (или начального состояния), т.е. от “пути”, которым газ шел к равновесию. Независимость от предыстории и постоянство во времени свойств газа в равновесии имеют своим следствием то, что равновесный газ можно описать небольшим числом макроскопических величин, характеризующих газ в целом (для идеального газа – ).
Определение: равновесным состоянием системы является ее наиболее вероятное состояние.
Итак, вероятность того, что число частиц в объеме будет отклоняться даже незначительно от ничтожна и быстро убывает с величиной этого отклонения. Но, тем не менее, число молекул в не всегда строго равно , а колеблется около этой величины. Отклонения числа частиц в объеме от наиболее вероятного значения – это флуктуации.
Приложение. Вычисление максимума вероятности биномиального распределения (традиционный способ).
.
Надо решить уравнение . Будем решать это уравнение для случая, когда и малы, т.е. , но при этом объем не слишком мал, так чтобы не было ничтожно мало. В этом случае максимум вероятности биноминального распределения достигается при достаточно больших и можно воспользоваться формулой Стирлинга для факториалов: .
Примечание. Формула Стирлинга получается следующим образом.
Возьмем логарифм от :
, где Dn = 1.
При больших можно считать . Тогда можно проинтегрировать полученное выражение
.
Теперь потенцируем и получаем формулу Стирлинга:
.
Используем полученное выражение:
Проводя преобразования, мы воспользовались тем, что велико (причем ) и известным пределом
.
Тогда имеем
.
Возьмем производную и приравняем её нулю , при этом вспоминая, что
.
Получаем
,
и тогда
.
Итак, развивая статистический (вероятностный) подход, мы нашли закон распределения частиц (молекул) по некоторому произвольно выбранному объему, предполагая, что в интересующем нас объеме находится газ невзаимодействующих частиц.
Среднее число частиц в произвольном объеме.
Вычислим теперь, используя распределение Бернулли, среднее число частиц в объеме по правилу, определяемому выражением (2.16)
, (3.13)
где .
Т.к. сумма, входящая в (3.13), согласно условию нормировки, равна единице, то
. (3.14)
Заменяя в (3.6) на , можем записать
. (3.15)
Сравнивая (3.11) и (3.14) сделаем ещё один важный вывод, вытекающий из статистического рассмотрения макроскопических систем. Из полученных выражений вытекает, что в состоянии равновесия наиболее вероятным числом молекул в некотором произвольно выбранном объеме является их среднее значение, что соответствует равномерному заполнению сосуда.
Источник
Функция плотности распределения для 106 молекул кислорода при −100, 20, 600 градусах Цельсия
Распределе́ние Ма́ксвелла – общее наименование нескольких распределений вероятности, которые описывают статистическое поведение параметров частиц идеального газа. Вид соответствующей функции плотности вероятности диктуется тем, какая величина: скорость частицы, проекция скорости, модуль скорости, энергия, импульс и т. д. – выступает в качестве непрерывной случайной величины. В ряде случаев распределение Максвелла может быть выражено как дискретное распределение по множеству уровней энергии.
Наиболее значимое распределение Максвелла записывается для модуля скорости частицы в непрерывном случае и имеет плотность:
и
где – формальная переменная, фактор определяется типом частиц и температурой, а множитель подбирается в зависимости от для обеспечения нормировки. Именно это выражение считается максвелловским распределением в математике, хотя для других параметров частиц аналитический вид распределения Максвелла будет иным.
Распределение Максвелла лежит в основе кинетической теории газов, объясняющей многие фундаментальные свойства газов, включая давление и диффузию. С его помощью вычисляются средние и наиболее вероятные скорости и энергии молекул газа. Оно также применимо для описания электронных процессов переноса и других явлений в физике и химии. Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Данное распределение является реализующимся с наивысшей вероятностью распределением изучаемого параметра.
Сфера применения распределения Максвелла[править | править код]
Требования к описываемой системе, примеры[править | править код]
Вопрос о применимости распределения Максвелла к конкретной системе равносилен вопросу о том, может ли эта система считаться идеальным газом с достаточной точностью. При этом система должна
- состоять из большого числа частиц и находиться в термодинамическом равновесии;
- являться изотропной;
- являться классической, то есть релятивистские и квантовые эффекты должны быть малы;
- быть столкновительно-доминируемой (взаимодействие частиц допускается лишь в случае, когда оно зависит только от относительного положения частиц, в частности, допускаются абсолютно упругие соударения).
Такой набор требований удовлетворяется в первую очередь в газах, например в воздухе, при обычных условиях. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. В первую очередь о нём обычно думают, как о распределении энергий молекул в газе, но оно может применяться к распределению скоростей и других параметров молекул. Чаще всего оно является непрерывным распределением по континууму изменения случайного параметра.
Во многих случаях, однако, условие доминирования упругих соударений над всеми другими процессами не выполняется даже приблизительно. Так, в физике ионосферы и космической плазмы, большое значение имеют процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы), в особенности для электронов. Использование распределения Максвелла в этом случае не только дало бы количественно неверные результаты, но и привело бы к качественно неправильной интерпретации соответствующих процессов.
Условия классического рассмотрения[править | править код]
В случаях, где квантовая дебройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, наблюдаются отклонения от распределения Максвелла из-за квантовых эффектов. Поэтому важен вопрос о границах применимости классического рассмотрения.
Соотношение неопределённостей (нередко упрощённо записываемое в форме где – неопределённости координаты и -проекции импульса, – постоянная Планка) имеет трёхмерный аналог вида где обозначает характерный линейный размер зоны локализации частицы. Чтобы неопределённости в координате и импульсе не играли роли и могла применяться классическая, а не квантовая механика, должно выполняться соотношение:
где – объём, на который в среднем приходится одна частица, равный обратной концентрации частиц газа. Если возвести обе части в квадрат, получится:
Учитывая, что и беря в качестве характерного значения энергии величину придём к:
( – температура вырождения, а – масса частицы).
При температурах ниже распределение Максвелла неприменимо.
Распределение Максвелла по состояниям[править | править код]
Распределение Максвелла можно записать как дискретное распределение по множеству состояний молекулы, нумеруемых символом :
.
Через и обозначены энергия молекулы в -м состоянии и число таких молекул, – температура системы, – общее число молекул в системе и – постоянная Больцмана. (Бывает, что вышеупомянутое уравнение записывается с множителем , обозначающим степень вырождения энергетических уровней. В этом случае нумерует не состояния, а энергии и сумма будет по энергиям, а не по состояниям). Поскольку скорость связана с энергией, последнее уравнение может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель известен как каноническая статистическая сумма.
Разновидности непрерывного распределения Максвелла[править | править код]
Представленный в этом разделе вывод распределений Максвелла, естественный для современной учебно-методической литературы, сильно отличается от вывода, предложенного самим Джеймсом Клерком Максвеллом и позже описанного с меньшим количеством предположений Людвигом Больцманом. Исторический вывод будет приведён в конце статьи.
Распределение по вектору импульса[править | править код]
В случае идеального газа из невзаимодействующих молекул вся энергия находится в форме кинетической энергии. Кинетическая энергия соотносится с импульсом частицы как:
,
где – квадрат вектора импульса , и уравнение (1) можно переписать как:
,
где – статсумма, соответствующая знаменателю в уравнении (1), – масса молекулы.
Если уровни энергии расположены достаточно густо, факт дискретности становится непринципиальным и можно считать, что энергии распределены непрерывно. Тогда отношение пропорционально функции плотности вероятности нахождения молекулы в состоянии с этими значениями компонент импульса. Таким образом:
.
Постоянная нормировки определяется из условия, в соответствии с которым вероятность того, что молекулы имеют какой-либо вообще импульс, должна быть равна единице. Поэтому интеграл уравнения (4) по всем значениям и должен быть равен единице. Можно показать, что:
.
Таким образом, чтобы интеграл в уравнении (4) имел значение 1 необходимо, чтобы
.
Подставляя выражение (6) в уравнение (4) и используя тот факт, что , мы получим:
.
Распределение по вектору скорости[править | править код]
Учитывая, что плотность распределения по скоростям пропорциональна плотности распределения по импульсам:
и используя мы получим:
,
что является распределением Максвелла по скоростям. Вероятность обнаружения частицы в бесконечно малом элементе около скорости равна:
Распределение по модулю импульса[править | править код]
Интегрируя, мы можем найти распределение по абсолютной величине импульса:
Распределение по энергии[править | править код]
Наконец, используя соотношения и , мы получаем распределение по кинетической энергии:
Распределение по проекции скорости[править | править код]
Распределение Максвелла для вектора скорости – является произведением распределений для каждого из трех направлений:
где распределение по одному направлению:
Это распределение имеет форму нормального распределения. Как и следует ожидать для покоящегося газа, средняя скорость в любом направлении равна нулю.
Распределение по модулю скорости[править | править код]
Обычно, более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, определяется как:
поэтому модуль скорости всегда будет больше или равен нулю. Так как все распределены нормально, то будет иметь хи-квадрат распределение с тремя степенями свободы. Если – функция плотности вероятности для модуля скорости, то:
,
где
таким образом, функция плотности вероятности для модуля скорости равна:
Вид функции соответствует приведённому в преамбуле с тем отличием, что там используется формальная переменная ради большей математической общности.
Характерные скорости молекул идеального газа[править | править код]
Уравнение (11) дает распределение скоростей, или, другими словами, долю молекул, имеющих специфическую скорость. Но часто более интересны другие величины. Ниже будут определены наиболее вероятная, средняя и среднеквадратичная скорости.
Наиболее вероятная скорость[править | править код]
Наиболее вероятная скорость, , – скорость, вероятность обладания которой любой молекулой системы максимальна и которая соответствует максимальному значению плотности вероятности распределения (а значит, соответствует моде этого распределения). Чтобы найти её, необходимо вычислить , приравнять нулю и решить относительно :
где – масса рассматриваемой частицы, – молярная масса.
Средняя арифметическая скорость[править | править код]
Подставляя и интегрируя, мы получим:
Среднеквадратичная скорость[править | править код]
Подставляя и интегрируя, мы получим:
Исторический вывод распределения Максвелла[править | править код]
Получим теперь формулу распределения так, как это делал сам Максвелл[1][2].
Рассмотрим пространство скоростных точек (каждую скорость молекулы представляем как точку (скоростную точку) в системе координат в стационарном состоянии газа. Выберем бесконечно малый элемент объёма . Так как газ стационарный, количество скоростных точек в остается неизменным с течением времени. Пространство скоростей изотропно, поэтому функции плотности вероятности для всех направлений одинаковы.
Максвелл предположил, что распределения скоростей по направлениям статистически независимы, то есть компонента скорости молекулы не зависит от – и – компонент.
– фактически вероятность нахождения скоростной точки в объёме .
Правая часть не зависит от и , значит и левая от и не зависит. Однако и равноправны, следовательно левая часть не зависит также и от . Значит данное выражение может лишь равняться некоторой константе.
Теперь нужно сделать принципиальный шаг – ввести температуру. Кинетическое определение температуры (как меры средней кинетической энергии движения молекул):
где Дж/К – постоянная Больцмана.
Ввиду равноправия всех направлений:
Чтобы найти среднее значение , проинтегрируем её вместе с функцией плотности вероятности от минус до плюс бесконечности:
Отсюда найдём :
Функция распределения плотности вероятности для (для и аналогично):
Теперь рассмотрим распределение по величине скорости. Вернемся в пространство скоростных точек. Все точки с модулем скорости лежат в шаровом слое радиуса и толщины , и – объём этого шарового слоя.
Таким образом, мы получили функцию плотности вероятности , являющуюся распределением Максвелла.
См. также[править | править код]
- Статистика Бозе – Эйнштейна
- Статистика Ферми – Дирака
- Статистика Максвелла – Больцмана
- Опыт Ламмерта
- Опыт Штерна
- Распределение Гиббса
- Распределение Бозе – Эйнштейна
- Распределение Ферми – Дирака
Примечания[править | править код]
Ссылки[править | править код]
https://www.falstad.com/gas/
Источник
