Равномерное вращение сосуда с жидкостью
Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.11).
На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и w2r. Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.
Рис. 2.11
Учитывая, что сила j нормальна к свободной поверхности, получим
отсюда
или после интегрирования
В точке пересечения свободной поверхности с осью вращения C = h, поэтому окончательно будем иметь
(2.10)
т. е. свободная поверхность жидкости является параболоидом вращения.
Максимальную высоту подъема жидкости можно определить исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.
На практике очень часто приходится иметь дело с вращением сосуда, заполненного жидкостью, вокруг горизонтальной оси. При этом угловая скорость w столь велика, что сила тяжести на порядок меньше центробежных сил, и ее действие можно не учитывать. Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.12). На выделенный элемент жидкости действуют силы давления и центробежная сила.
Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp, получим следующее уравнение равновесия выделенного объема в направлении радиуса
или
Рис. 2.12
После интегрирования
Постоянную C найдем из условия, что при r = r0 p = p0.
Следовательно
Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:
(2.11)
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.
Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr. Используя формулу (2.11), получим
а затем следует выполнить интегрирование в требуемых пределах.
При большой скорости вращения жидкости получается значительная суммарная сила давления на стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.
Источник
Содержание:
- Равномерное вращение сосуда с жидкостью
Равномерное вращение сосуда с жидкостью
Равномерное вращение сосуда с жидкостью. Возьмите открытый цилиндрический контейнер с жидкостью и скажите ему вращаться с постоянной угловой скоростью o) вокруг своей вертикальной оси. Жидкость постепенно приобретает ту же угловую скорость, что и емкость, и ее свободная поверхность changes. In (рис.1.18). В этом случае на жидкость действуют 2 массовые силы. Гравитационные и центробежные силы равны% и<B2, если они отнесены к единице массы. Результирующая массовая сила/увеличивается с увеличением радиуса на 2-ю составляющую, а угол наклона относительно горизонта уменьшается.
В центральной части уровень жидкости уменьшается, в стенке уровень жидкости увеличивается*, и вся свободная поверхность жидкости становится определенной вращающейся поверхностью.
Людмила Фирмаль
- Эта сила перпендикулярна свободной поверхности жидкости, поэтому больший радиус приводит к большему наклону этой поверхности.Найдите уравнение для кривой BWT в системах координат b и r и поместите начало координат в центр дна контейнера.Учитывая, что сила 7 нормальна Из рисунка, который мы нашли, кривая BWT меньше Осы = yb} yy = ω^ y/, где-o> yy s1y /§、 Или ешьте интегрирование r = s * r2 / {28)+ C На пересечении кривой A OB с осью вращения r-0,% = k =■* C, наконец 5 = * = ^ / a) 2r2 /(2^), (1.34) То есть кривая АОБ-это парабола, а свободная поверхность жидкости-парабола. Другие ровные поверхности имеют такую же форму.
Формула (1.34) позволяет определить положение свободной поверхности b-слоя, например, максимальную высоту подъема жидкости H и высоту положения разрядника парапроидов при определенной угловой скорости w. It это необходимо для этого Используйте больше уравнений объема! Объем неподвижной жидкости равен объему при вращении. Чтобы определить закон изменения давления вращающейся жидкости в функции радиуса и высоты, мы делаем то же самое с§ 1.5. Выберите вертикальный цилиндрический объем жидкости с дном в виде базовой горизонтальной платформы&8 (точка M) при любом радиусе r и высоте’%, запишите равновесное состояние в вертикальном направлении.
- Учитывая формулу (1.34). П (13 [А-Р + ко? Р2 /(2^)] п#/Ой а) cos а-0. После снижения、 P = P <1 + [k * + <22г* 1 {2§)]§r. (1.35) Это означает, что давление увеличивается пропорционально радиусу x и уменьшается пропорционально высоте i. Если в контейнере есть крыша, которая вращается вокруг вертикальной оси, а верх заполнен жадностью, то его форма не может быть изменена, но давление изменяется в соответствии с формулой(1.35).На рисунке 1.19 показана эпюра давления вдоль крышки контейнера, ССТ и дна. Дело в том, что вращение сосуда в жидкости часто учитывается, если из-за очень большой угловой скорости он способен игнорировать силу тяжести по сравнению с центробежной force.
In в этом случае индикатор изменения давления жидкости легко получить по следующей формуле: $ 2. (1.35), следует использовать r = k = 0. Более того, если давление p0 действует на r = r0 вместо центра, то вместо уравнения (1.35) Р = Ро рсо2(Р2-Р?) / 2,(1 * 35 ’) Часто необходимо определить давление жидкости, вращающейся вместе с контейнером со стенкой, перпендикулярной оси вращения (или кольцевой части этой стенки).Для этого сначала необходимо выразить давление, обусловленное основной кольцевой областью радиуса r и шириной d де = п-[ро + ро> р(р *-р*) / 2] 2л Р Затем он выполняет интеграцию в требуемых пределах.
Угол, образованный осью вращения вертикального сосуда, незначителен, и горизонтальной плоскостью можно считать цилиндр с общей осью(осью вращения сосуда).
Людмила Фирмаль
- При большой угловой скорости жидкости получается очень большое суммарное давление, которое прикладывается к walls. It применяется в фрикционных муфтах, требующих большой силы нормального давления для соединения 2-х валов. Используя описанный выше способ, определите осевое усилие жидкости на крыльчатке центрифуги и крышке центробежного насоса. Ту же формулу, что и для рассматриваемого относительного покоя, можно вывести интегрированием дифференциального уравнения равновесия жидкости (1.24).
Поместив начало координат*в центр дна емкости и направив ось 2 вертикально вверх、 Х-потому, что(р, х)= в = проекте » w2r » ео(р, г) о> 2(/; 2 =Подставляя эти величины в уравнение (1.24), c1x {<a2y, yy% yr > p / p、 Или УГ-ryu2 (xЗхф уду уду ))учитывая, что πг+ yyy=((r72)), после интегрирования、 п = ч / 2-р ^ р -] с ’2 за пределами 165 Итак, если r = 0 и r = A, то p = p0. В итоге я наконец-то получил* П-По +(А-2)+ п(03G2 / 2. Уравнение для свободной поверхности жидкости известно как P = Р0.После сокращений и преобразований、 2 ^ soag * /(2#) 4-A、 Он соответствует ранее полученным выражениям (1.34) и (1.35).
Смотрите также:
Методические указания по гидравлике
Возможно эти страницы вам будут полезны:
- Сила давления жидкости на криволинейные стенки. Плавание тел.
- Прямолинейное равноускоренное движение сосуда с жидкостью.
- Кинематика и динамика жидкости.
- Расход. Уравнение расхода.
Источник
Вращение сосуда с жидкостью вокруг вертикальной оси
Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость w вращения вокруг вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в центральной части уровень жидкости понизится, у стенок – повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 2.15).
Рис. 2.15
На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и . Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому угол наклона поверхности к горизонту возрастает с увеличением радиуса. Найдем уравнение положения свободной поверхности.
Учитывая, что сила нормальна к свободной поверхности, получим , отсюда или после интегрирования .
В точке пересечения свободной поверхности с осью вращения C=h и r=0, поэтому окончательно будем иметь
, (2.10)
где .
Таким образом, свободная поверхность жидкости является параболоидом вращения. Максимальную высоту подъема жидкости можно определить, используя выражение (2.10) и исходя из равенства объемов неподвижной жидкости и жидкости во время вращения.
Запишем закон изменения давления во вращающейся жидкости в функции радиуса и глубины относительно верхней точки жидкости (без вывода):
.
Вращение сосуда с жидкостью вокруг горизонтальной оси
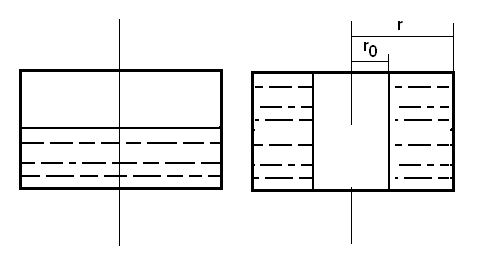
При таком вращении угловая скорость w столь велика, что (действие силы тяжести можно не учитывать). Закон изменения давления в жидкости для этого случая получим из рассмотрения уравнения равновесия элементарного объема с площадью основания dS и высотой dr, взятой вдоль радиуса (рис. 2.16). На выделенный элемент жидкости действуют силы давления и центробежная сила.
Рис. 2.16
Обозначив давление в центре площадки dS, расположенной на радиусе r, через p, а в центре другого основания объема (на радиусе r + dr) через p + dp (разложили p в ряд Тейлора, но так как в данном случае p зависит только от r, то dr/dr сократился), получим следующее уравнение равновесия выделенного объема в направлении радиуса
или .
После интегрирования получим . Постоянную C найдем из условия, что при r = rp = p0, следовательно, .
Подставив ее значение в предыдущее уравнение, получим связь между p и r в следующем виде:
. (2.11)
Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью – осью вращения жидкости.
Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к его оси вращения. Для этого определим силу давления, приходящуюся на элементарную кольцевую площадку радиусом r и шириной dr. Используя формулу (2.11), получим
,
а затем следует выполнить интегрирование в требуемых пределах:
.
Если равно внешнему давлению, то .
При большой скорости вращения жидкости получается значительная суммарная сила давления Fб на боковую стенку. Это используется в некоторых фрикционных муфтах, где для сцепления двух валов требуется создание больших сил давления.
Приведем выражение для определения силы Fб без вывода:
, где – длина цилиндра.
Источник
Возьмем открытый цилиндрический сосуд
с жидкостью и сообщим ему вращение с
постоянной угловой скоростью ω вокруг
его вертикальной оси. Силы трения о
стенки вращающегося сосуда будут
увлекать за собой жидкость. Она постепенно
приобретет ту же угловую скорость, что
и сосуд, находясь по отношению к сосуду
в покое. Свободная поверхность жидкости
изменится.
В центральной части уровень жидкости
опустится, у стенок она поднимется, и
вся свободная поверхность жидкости
станет поверхностью вращения (рис.4.6).
На жидкость будут действовать силы
давления, силы тяжести и силы инерции
переносного движения. Частица жидкости
будет находиться под действием ускорения
силы тяжести и центростремительного
ускорения, а равное ему ускорение силы
инерции будет центробежным. Единичная
массовая сила тяжести Fg
= gи единичная
массовая центробежная силаFцб
= ω2r.
Проекции этих сил на оси координат дадут
следующие выражения
X = (V2/r)Cos(r^x) = ω2r
Cos(r^x)= ω2X
Y = (V2/r)Cos(r^y) = ω2r
Cos(r^у)= ω2Y,
Z = -g

Подставляя эти проекции в дифференциальное
уравнение поверхности равного давления
и интегрируя :
X*dх+У*dy+Z*dz
= 0,
получим ρ(ω2/2)
(X2
+ Y2)
– ρgz
+ С=
0.
Уравнение свободной
поверхности, например, получим, при
нулевых условиях: Р
= const,
х = у = 0,
z= z,где
координата вершины параболоида свободной
поверхности. ТогдаС
=ρgz.
ρ(ω2/2)
(X2
+ Y2)
– ρgz
+ ρgz
= 0,
(ω2/2)
(X2
+ Y2)
=g(z
– z)
и после деления на g
уравнение свободной поверхности
получит вид
![]()
(4.22)
Таким образом, поверхности равного
давления, в том числе и свободная
поверхность, образуют семейство
параболоидов, сдвинутых вдоль вертикальной
оси. Каждому значению рсоответствует свой параболоид, положение
которого определяет константа С.
Эти поверхности будут
конгруэнтными параболоидами вращения
с осью Oz.
Один из этих параболоидов – свободная
поверхность жидкости, где Р=
Ратм.
Две геометрические фигуры
называются конгруэнтными, если их можно
совместить одну с другой, изменив их
положение в пространстве.
Подставляя проекции массовых сил в
дифференциал давления
dp= ρ(Xdx
+ Ydy
+ Zdz),
получим dp= ρω2
(Xdx
+ Ydy)
–ρgdz,
вынесем знак дифференциала за скобки,
dp= ρd[(ω2/2)
(X2
+ Y2)]
–ρgdz,
и проинтегрировав, получим выражение
для определения давления в любой точке
p= ρ(ω2/2)
(X2
+ Y2)
–ρgz
+ С1,
(4.21)
Значение константы для
свободной поверхности
Р = Р,
x=y=0,
z
= z:
С1
= Р
+ ρgz0.
Получим уравнение для определения
давления в любой точке:
![]()
(4.22)
Пользуясь этими уравнениями можно
определить положение свободной
поверхности и давление в сосуде.
Максимальная высота Н подъема жидкости
в параболоиде со свободной поверхностью
может быть определена, следующим образом.
![]()
На практике часто рассматривается
вращение сосуда с жидкостью, когда
угловая скорость ω столь велика, что
силой тяжести можно пренебречь по
сравнению с центробежными силами. При
этом закон изменения давления в жидкости
легко получить из формулы (4.22), в которой
следует принять g(z
– z)= 0.
Поверхности уровня примут вид цилиндров
с общей осью – осью вращения сосуда.
Если сосуд не был заполнен перед началом
вращения, давление Рбудет действовать не в центре, а приr
= r,
вместо выражения (4.22) будем иметь
Р = Р + ρ ω2
(r —r2)/2g,(4.23)
Часто бывает необходимо определить
силу давления вращающейся вместе с
сосудом жидкости на его стенку, нормальную
к оси вращения (или на кольцевую часть
этой стенки).
Для этого необходимо выразить сначала
силу давления, приходящуюся на элементарную
кольцевую площадкуdS
=2πrdrрадиусомrи ширинойdr;

Уравнение, выражающее величину давления
имеет вид
![]()
При определении давления
на верхнюю крышку где Z=0,
Z0
может быть больше нуля Z0>0![]() ,
,
равно нулю![]() и
и
меньше нуля
![]()
В первом случае
![]()
а затем выполнить интегрирование в
требуемых пределах.
При большой угловой скорости жидкости
можно получить весьма значительную
суммарную силу давления на стенку. Этот
эффект используется в некоторых
фрикционных муфтах, где для осуществления
сцепления двух валов требуется создание
больших сил нормального давления.
Способ, указанный выше, применяют для
определения силы осевого давления
жидкости на рабочие колеса центробежных
насосов, а также на крышки центрифуг.
5-я лекция.
Соседние файлы в папке Лекции и семинары
- #
- #
- #
Источник
В случае равномерного вращения цилиндрического сосуда вокруг вертикальной оси с угловой скоростью ш (рис. 2.25) уравнение любой изобарической поверхности (р = const) имеет вид
где z — координата точки пересечения свободной поверхности с осью вращения;
Изобарические поверхности — параболоиды вращения, ось которых совпадает с осью Oz, а вершины смещены вдоль этой
Рис. 2.25. Вращение цилиндрического сосуда вокруг вертикальной оси оси. Форма изобарических поверхностей не зависит от плотности жидкости.
Изменение давления по вертикали
т.е. такое же, как в неподвижном сосуде.
Пример 2.6. Вертикальный цилиндрический сосуд диаметром D = 40 см и высотой Н = 100 см наполнен до половины водой (рис. 2.26). Определить, с каким предельным числом оборотов можно вращать этот сосуд вокруг сто геометрической вертикальной оси, чтобы из него нс выливалась вода, а также силу давления жидкости на дно сосуда.
Рис. 2.26. Поверхности равного давления во вращающемся сосуде
Решение. Из рис. 2.26 видно, что Н = Zq + h. В соответствии с формулами (2.16) и (2.17)
Тогда
Начальный уровень Л0 в резервуаре по условию равен Н/2. Следовательно,
Соответственно
Предельное число оборотов
(об/мин).
Для определения силы давления жидкости на дно сосуда найдем распределение избыточного давления, полагая р0 = р ‘.
Координату z0 вершины параболоида определим по формуле
т.с. параболоид свободной поверхности касается дна сосуда. Тогда
Для точек на дне сосуда (z = 0) избыточное давление определим следующим образом:
Силу давления на дно сосуда найдем как сумму элементарных сил давления, действующих на элементарные кольцевые площадки, равные 2nrdr.
Задачи для самостоятельного решения
- 2.18. Призматический сосуд дайной 3 м и шириной 1 м, перемещающийся горизонтально с постоянным ускорением 0,4g, разделен на два отсека, заполненных водой до высот 1 м и 1,75 м соответственно. Определить результирующую силу давления воды на перегородку, разделяющую отсеки.
- 2.19. Измеритель ускорения тела, движущегося горизонтально, представляет собой закрепленную на нем U-образную трубку малого диаметра, наполненную жидкостью. Определить, с каким ускорением движется тело, если при движении в коленах измерителя установилась разность уровней жидкости 75 мм при расстоянии между уровнями 250 мм.
Рис. 2.27. К определению поверхности равного давления при равномерном вращении сосуда с жидкостью
Рис. 2.28. К определению относительного равновесия жидкости в закрытом равномерно вращающемся сосуде
2.20. Сосуд, имеющий форму усеченного конуса, заполнен водой до половины высоты и приводится во вращение вокруг своей вертикальной оси (рис. 2.27). Определить наибольшее число оборотов, при котором вода не будет выливаться из сосуда, если И =
= а = 0,8 м и угол а = 45°.
- 2.21. Закрытый цилиндрический сосуд, радиус которого г, = 50 см, равномерно вращается относительно вертикальной оси. При этом уровень жидкости в открытой трубке малого диаметра, установленной на расстоянии г2 = 35 см от центра, расположен на высоте И =
- 40 см (рис. 2.28). Плотность жидкости равна 800 кг/м3; атмосферное давление 760 мм рт. ст. Определить наибольшую
угловую скорость, при которой сохранится относительное равновесие жидкости. Давление насыщенных паров жидкости равно 49 кПа[1].
2.22. Закрытый сверху крышкой цилиндр диаметром 0,9 м и высотой 0,8 м содержит 0,35 м3 воды и вращается вокруг вертикальной оси с угловой скоростью 100 с1. Определить усилия, действующие при этом на крышку цилиндра, если давление на поверхности воды атмосферное.
Источник
