Равновесие жидкости в цилиндрическом сосуде
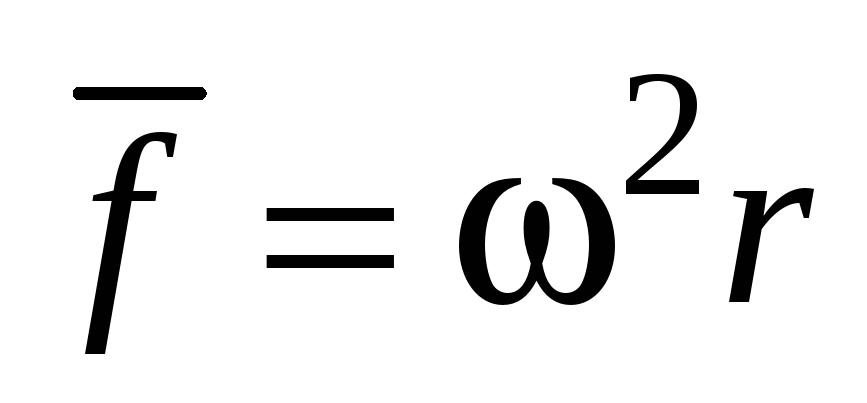
В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать
различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.
1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции.
Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле
p = p0 + ρ·(g·z ± a·x),
Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:
g·z = ± a·x
или
z/x = tg α = ± a/g,
где α – угол наклона свободной поверхности жидкости к горизонту.
Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l)
высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.
Если сосуд движется равномерно (а = 0), уравнение приводим к виду:
p = p0 + ρ·g·z = p0·γ
В этом случае поверхность равного давления представляет горизонтальную плоскость.
2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.
Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:
p = p0 + γ·((ω2·r2)/(2·g) – z)
Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:
z = (ω2·r2)/(2·g) = u2/(2·g),
где окружная скорость u = ω·r (r — радиус вращения точки).
Высота параболоида вращения:
h = ω2·r20/(2·g),
где r0 – радиус цилиндрического сосуда.
Сила давления жидкости на дно сосуда:
P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),
где h0 – начальная глубина жидкости в сосуде до момента его вращения.
Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).
3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.
В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.
Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).

При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).
Распределение давления по глубине жидкости определяется выражением:
p = p0 + γ·ω2·(r2 – r20)/(2·g)
где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.
Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.
Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в.
Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Источник
Относительным равновесием жидкости называется такое состояние, при котором отдельные ее частицы не смещаются одна относительно другой, а также стенок сосуда – и вся масса жидкости движется как твердое тело.
В абсолютно покоящейся жидкости (сосуд неподвижен) действующей массовой силой (в поле сил тяжести) является только сила тяжести. При относительном покое к ней добавляется еще массовая сила – сила инерции.
Законы относительного равновесия жидкости находят широкое применение в промышленности, а именно, в измерительной технике (жидкостные тахометры), в металлургии (центробежное литье) и других областях техники.
При изучении относительного равновесия необходимо заниматься, во-первых, установлением закона распределения давления внутри жидкости, а, во-вторых, определением формы поверхности равного давления, т.е. такой поверхности, все точки которой испытывают одинаковое давление.
Первая задача решается с помощью дифференциального уравнения гидростатики, справедливого для всех случаев равновесия
(3.1)
Вторая задача – с помощью дифференциального уравнения поверхности равного давления
, (3.2)
где x, y, z– координаты точек жидкости в системе отсчета, связанной с аппаратом (сосудом); P=f(x,y,z) – давление в жидкости; r – плотность жидкости; X, Y, Z– проекции единичной массовой силы q на оси координат.
При движении сосуда в поле сил тяжести вектор единичной массовой силы в каждой точке жидкости представляет собой сумму единичной силы тяжести и единичной силы инерции переносного движения:
; , (3.3)
где – переносное ускорение в точке жидкости.
В случае относительного равновесия жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью (рис. 3.1), вектор массовой силы находится как сумма вектора
единичной силы тяжести и вектора единичной центробежной силы инерции . Проекции на оси координат представляются выражениями
; ; (3.4)
Интегрирование уравнений (3.1) и (3.2) с учетом зависимостей (3.4) дает, во-первых, закон распределения давления в жидкости
) (3.5)
и, во-вторых, уравнение свободной поверхности жидкости, которое имеет вид параболоида вращения
, (3.6)
где P- давление в точке жидкости с координатами r и z; – давление на свободную поверхность жидкости в сосуде; – координата вершины параболоида (рис. 3.1); R – радиус сосуда; H – уровень воды в сосуде при .
Из уравнения (3.6) при r=0 определяется координата вершины параболоида
, (3.7)
а при r=R координата верхней кромки параболоида
(3.8)
Из зависимости (3.8) можно определить максимальную угловую скорость вращения сосуда, при которой жидкость не будет переливаться из него, т.е., когда
, (3.9)
где – высота сосуда.
Цель работы– экспериментальное определение формы свободной поверхности жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью, и сравнение результатов измерений с теоретическими расчетами.
Описание установки
Вертикальный цилиндрический прозрачный сосуд 1 (радиусом R= 0,11 м и высотой = 0,22 м) заполняется водой и приводится во вращение с помощью электродвигателя 2 (рис. 3.2) и ременной передачи со ступенчатыми шкивами 3. Для вращения сосуда 1 с разными скоростями ремень 4 перемещается вдоль ступенчатых шкивов 3. Число оборотов сосуда 1 измеряется с помощью тахометра. Уровень воды в сосуде 1 измеряется линейкой 5.
Проведение опытов и измерения
1. Перед началом эксперимента измеряется уровень воды в сосуде 1 с помощью линейки 5 (рис. 3.2). Этот уровень рекомендуется устанавливать на отметке H=0,08¸0,1 м. Если H<0,07 м сосуд необходимо долить водой.
2. Устанавливается ремень 4 в одно из положений и включается электродвигатель 2. Выжидают некоторое время, пока жидкость в сосуде 1 не придет в состояние относительного равновесия и стабилизации формы свободной поверхности (параболоида вращения). После этого производятся следующие измерения:
– частота вращения сосуда n;
– координаты верхней кромки параболоида вращения zви
– координаты вершины параболоида вращения zои.

3. Измерения производятся для нескольких опытов с разными частотами вращения n. Все результаты измерений заносятся в табл. 3.1.
Вычисления и составление отчета
1. Определяется угловая скорость вращения сосуда по формуле
, рад/с, (3.10)
где n – частота вращения сосуда, мин-1.
2. Вычисляются теоретические координаты кривой свободной поверхности жидкости в сосуде, а именно, координаты вершины параболоида z по формуле (3.7), а верхней кромки zв – по формуле (3.8).
3. По зависимости (3.9) определяется максимальная угловая скорость вращения сосуда w max.
4. Определяется степень отклонения (относительная погрешность) в % между измеренными и теоретическими координатами вершины и верхней кромки параболоида вращения по формулам
(3.11)
(3.12)
Все результаты вычислений заносятся в табл. 3.1.
5. По результатам измерений и вычислений строятся экспериментальная и теоретическая кривые свободной поверхности жидкости в меридиальном сечении сосуда (рис. 3.3). Промежуточные точки между z и zв теоретической кривой находятся по формуле (3.6), задаваясь значениями r. Экспериментальная кривая строится по трем точкам, т.е. по zои , zви и zR/2 при r=R/2=0,055 м, которая находится по зависимости
 |
Таблица 3.1
.
| № опыта | Измеренные величины | Расчетные величины | ||||||||
| Высота уровня жидкости в сосуде H, м | Частота вращения сосуда n, мин-1 | Угловая скорость вращения сосуда w, рад/с | Координаты параболоида вращения | Максимальная угловая скорость вращения сосуда w max, рад/с | Координаты параболоида вращения | Относительная погрешность | ||||
| вершины Z0и, м | верхней кромки Zви, м | вершины Z0, м | верхней кромки Zв, м | e0, % | eв, % | |||||
| 1. | ||||||||||
| 2. | ||||||||||
| 3. | ||||||||||
| 4. | ||||||||||
| 5. | ||||||||||
| 6. |
, м (3.13)
Сравнение полученных кривых позволяет судить о том, насколько экспериментальная кривая свободной поверхности жидкости во вращающемся сосуде близка к теоретической кривой, т.е. к параболе.
В выводах следует отметить: какая форма свободной поверхности жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью; причина образования параболоида вращения и его зависимость от частоты вращения сосуда; можно ли использовать и каким образом сосуд с жидкостью в качестве водяного тахометра.
Источник
Основы теории и цель работы
Относительным равновесием жидкости называется такое состояние, при котором отдельные ее частицы не смещаются одна относительно другой, а также стенок сосуда – и вся масса жидкости движется как твердое тело.
В абсолютно покоящейся жидкости (сосуд неподвижен) действующей массовой силой (в поле сил тяжести) является только сила тяжести. При относительном покое к ней добавляется еще массовая сила – сила инерции.
Законы относительного равновесия жидкости находят широкое применение в промышленности, а именно, в измерительной технике (жидкостные тахометры), в металлургии (центробежное литье) и других областях техники.
При изучении относительного равновесия необходимо заниматься, во-первых, установлением закона распределения давления внутри жидкости, а, во-вторых, определением формы поверхности равного давления, т.е. такой поверхности, все точки которой испытывают одинаковое давление.
Первая задача решается с помощью дифференциального уравнения гидростатики, справедливого для всех случаев равновесия
(3.1)
Вторая задача – с помощью дифференциального уравнения поверхности равного давления
, (3.2)
где x, y, z– координаты точек жидкости в системе отсчета, связанной с аппаратом (сосудом); P=f(x,y,z) – давление в жидкости; r – плотность жидкости; X, Y, Z– проекции единичной массовой силы q на оси координат.
При движении сосуда в поле сил тяжести вектор единичной массовой силы в каждой точке жидкости представляет собой сумму единичной силы тяжести и единичной силы инерции переносного движения:
; , (3.3)
где – переносное ускорение в точке жидкости.
В случае относительного равновесия жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью (рис. 3.1), вектор массовой силы находится как сумма вектора
единичной силы тяжести и вектора единичной центробежной силы инерции . Проекции на оси координат представляются выражениями
; ; (3.4)
Интегрирование уравнений (3.1) и (3.2) с учетом зависимостей (3.4) дает, во-первых, закон распределения давления в жидкости
) (3.5)
и, во-вторых, уравнение свободной поверхности жидкости, которое имеет вид параболоида вращения
, (3.6)
где P- давление в точке жидкости с координатами r и z; – давление на свободную поверхность жидкости в сосуде; – координата вершины параболоида (рис. 3.1); R – радиус сосуда; H – уровень воды в сосуде при .
Из уравнения (3.6) при r=0 определяется координата вершины параболоида
, (3.7)
а при r=R координата верхней кромки параболоида
(3.8)
Из зависимости (3.8) можно определить максимальную угловую скорость вращения сосуда, при которой жидкость не будет переливаться из него, т.е., когда
, (3.9)
где – высота сосуда.
Цель работы– экспериментальное определение формы свободной поверхности жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью, и сравнение результатов измерений с теоретическими расчетами.
Описание установки
Вертикальный цилиндрический прозрачный сосуд 1 (радиусом R= 0,11 м и высотой = 0,22 м) заполняется водой и приводится во вращение с помощью электродвигателя 2 (рис. 3.2) и ременной передачи со ступенчатыми шкивами 3. Для вращения сосуда 1 с разными скоростями ремень 4 перемещается вдоль ступенчатых шкивов 3. Число оборотов сосуда 1 измеряется с помощью тахометра. Уровень воды в сосуде 1 измеряется линейкой 5.
Проведение опытов и измерения
1. Перед началом эксперимента измеряется уровень воды в сосуде 1 с помощью линейки 5 (рис. 3.2). Этот уровень рекомендуется устанавливать на отметке H=0,08¸0,1 м. Если H<0,07 м сосуд необходимо долить водой.
2. Устанавливается ремень 4 в одно из положений и включается электродвигатель 2. Выжидают некоторое время, пока жидкость в сосуде 1 не придет в состояние относительного равновесия и стабилизации формы свободной поверхности (параболоида вращения). После этого производятся следующие измерения:
– частота вращения сосуда n;
– координаты верхней кромки параболоида вращения zви
– координаты вершины параболоида вращения zои.
3. Измерения производятся для нескольких опытов с разными частотами вращения n. Все результаты измерений заносятся в табл. 3.1.
Вычисления и составление отчета
1. Определяется угловая скорость вращения сосуда по формуле
, рад/с, (3.10)
где n – частота вращения сосуда, мин-1.
2. Вычисляются теоретические координаты кривой свободной поверхности жидкости в сосуде, а именно, координаты вершины параболоида z по формуле (3.7), а верхней кромки zв – по формуле (3.8).
3. По зависимости (3.9) определяется максимальная угловая скорость вращения сосуда w max.
4. Определяется степень отклонения (относительная погрешность) в % между измеренными и теоретическими координатами вершины и верхней кромки параболоида вращения по формулам
(3.11)
(3.12)
Все результаты вычислений заносятся в табл. 3.1.
5. По результатам измерений и вычислений строятся экспериментальная и теоретическая кривые свободной поверхности жидкости в меридиальном сечении сосуда (рис. 3.3). Промежуточные точки между z и zв теоретической кривой находятся по формуле (3.6), задаваясь значениями r. Экспериментальная кривая строится по трем точкам, т.е. по zои , zви и zR/2 при r=R/2=0,055 м, которая находится по зависимости
Таблица 3.1
.
| № опыта | Измеренные величины | Расчетные величины | ||||||||
| Высота уровня жидкости в сосуде H, м | Частота вращения сосуда n, мин-1 | Угловая скорость вращения сосуда w, рад/с | Координаты параболоида вращения | Максимальная угловая скорость вращения сосуда w max, рад/с | Координаты параболоида вращения | Относительная погрешность | ||||
| вершины Z0и, м | верхней кромки Zви, м | вершины Z0, м | верхней кромки Zв, м | e0, % | eв, % | |||||
| 1. | ||||||||||
| 2. | ||||||||||
| 3. | ||||||||||
| 4. | ||||||||||
| 5. | ||||||||||
| 6. |
, м (3.13)
Сравнение полученных кривых позволяет судить о том, насколько экспериментальная кривая свободной поверхности жидкости во вращающемся сосуде близка к теоретической кривой, т.е. к параболе.
В выводах следует отметить: какая форма свободной поверхности жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью; причина образования параболоида вращения и его зависимость от частоты вращения сосуда; можно ли использовать и каким образом сосуд с жидкостью в качестве водяного тахометра.
Лабораторная работа № 4
Источник
В
состоянии покоя жидкость заполняла
сосуд до высоты
![]() ,
,
и свободная поверхность была горизонтальной
плоскостью.
При вращении сосуда вокруг вертикальной
оси с угловой скоростью
![]()
на каждую частицу жидкости, кроме
единичной силы тяжести
![]() ,
,
действует единичная инерционная сила
(центробежная)
![]() .
.
Результирующая единичная сила:
![]() .
.
Под действием центробежной силы свободная
поверхность искривляется – в центре
жидкость опускается, у стенок поднимается.
Свободная поверхность принимает форму
параболоида вращения, описываемую
уравнением:
![]() .
.
Остальные поверхности уровня представляют
такие же параболоиды, но с вершинами,
смещенными по оси вращения и описываемые
уравнением:
![]() ,
,
где ![]() .
.
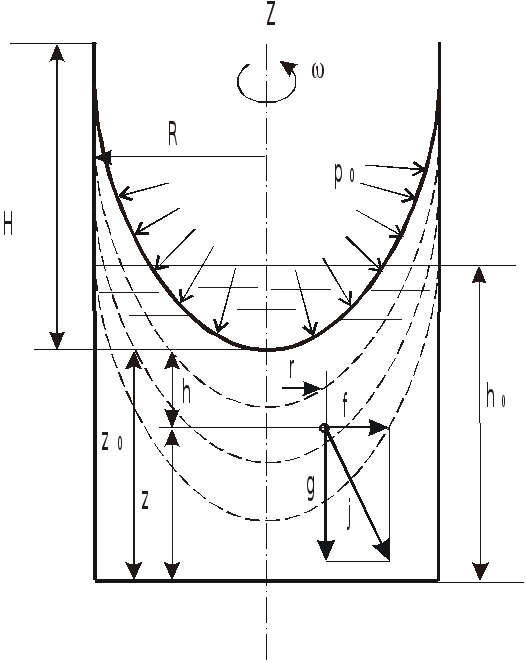
Высота параболоида
![]()
не зависит от плотности жидкости.
Закон распределения давления в жидкости
выражается уравнением:
![]() .
.
Для оси вращения (![]() )
)
закон распределения давления такой же,
как и в неподвижном сосуде:
![]() ;
;
![]() .
.
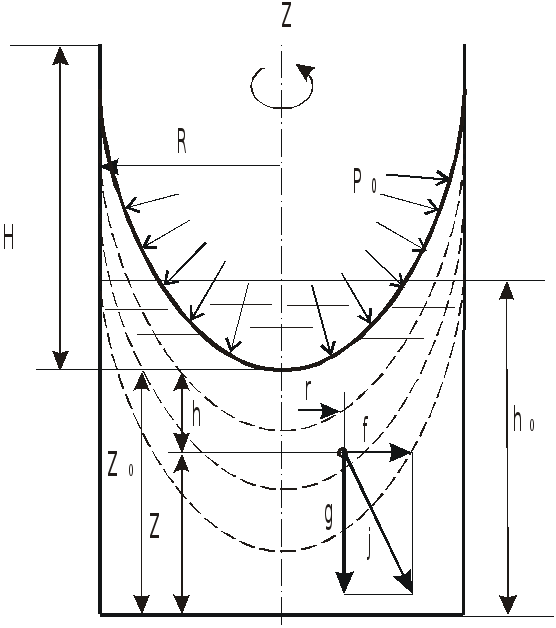
Эпюры распределения давления на дно и
стенки сосуда приведены на рисунке.
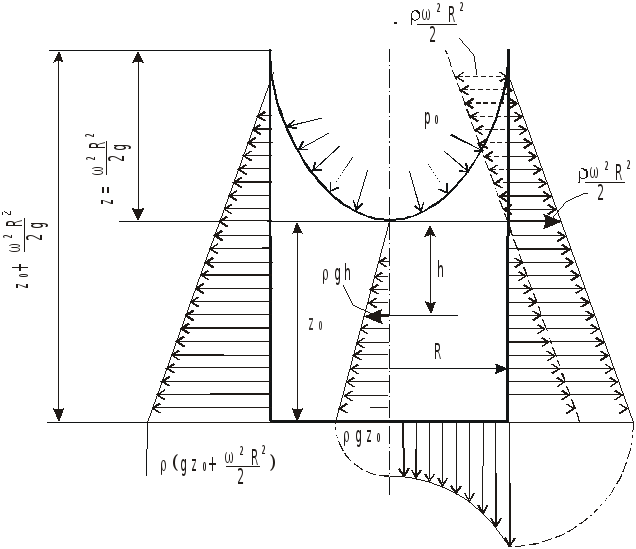
К
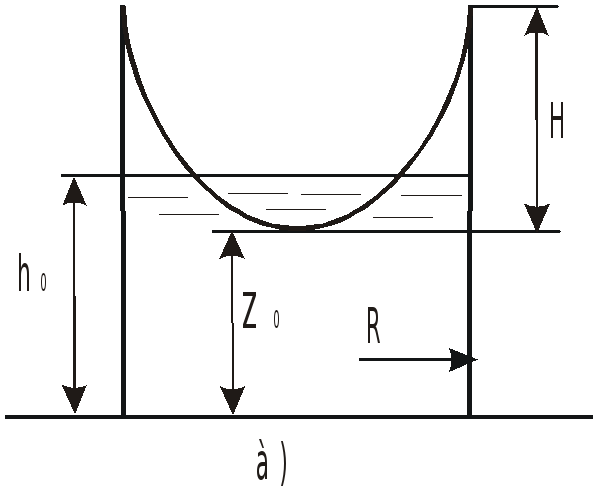
оордината
![]()
– вершины параболоида свободной
поверхности при заданной угловой
скорости
![]()
определяется объемом заключенной в
сосуде жидкости.
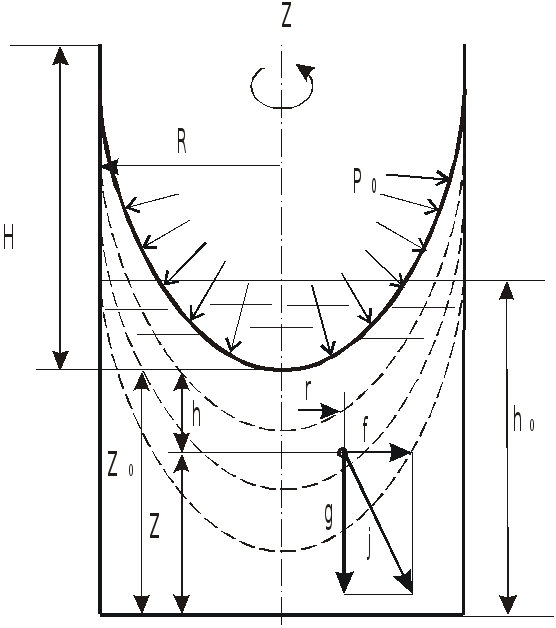
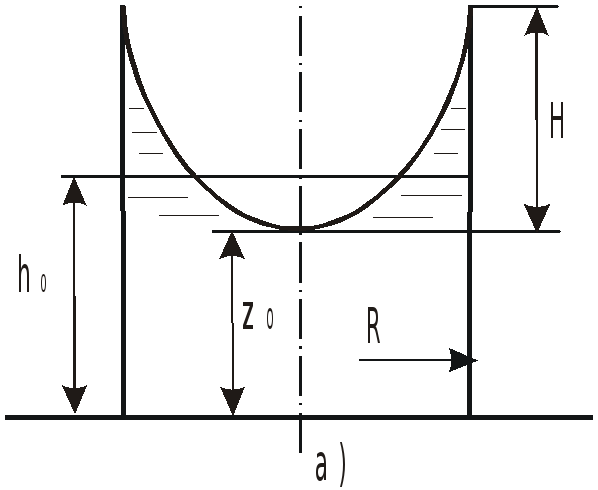
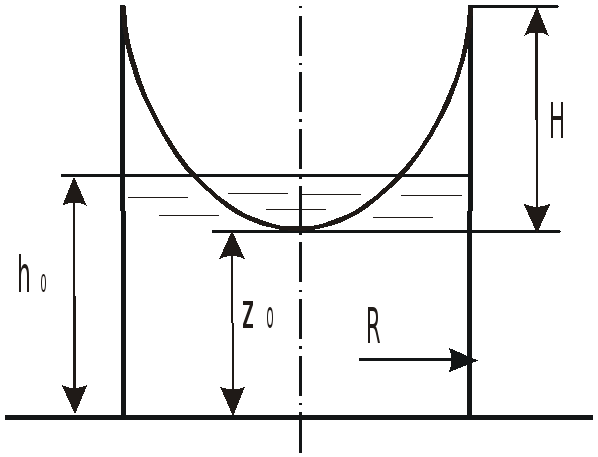
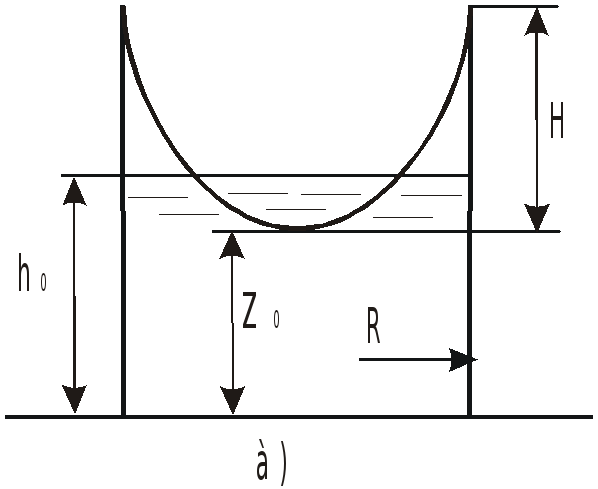
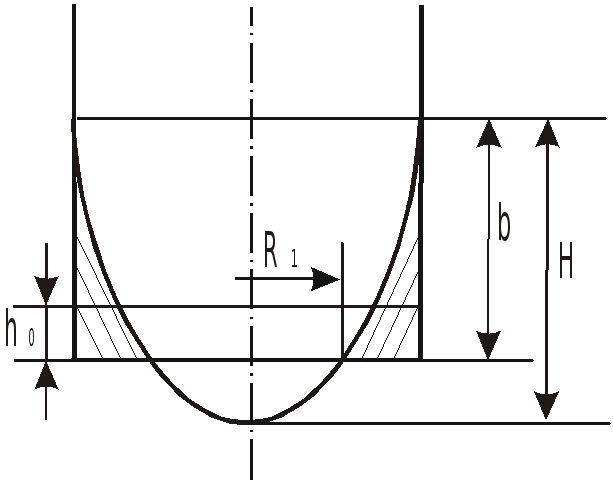
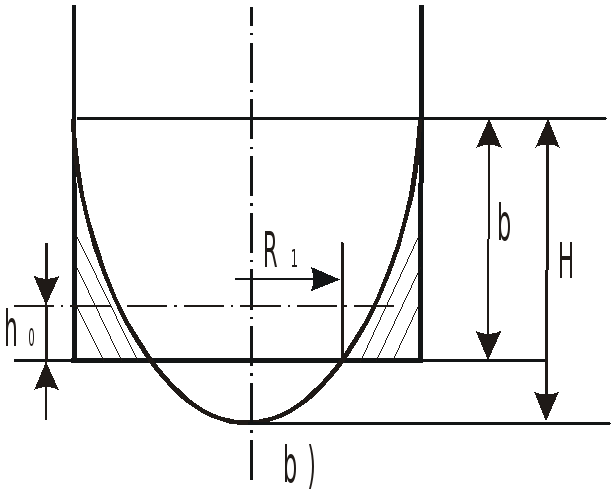
При решении задач могут встретиться
случаи, когда свободная поверхность не
пересекает дно сосуда (a)
или пересекает его (b).
При этом используются следующие
соотношения для определения
![]()
– объема жидкости.
В
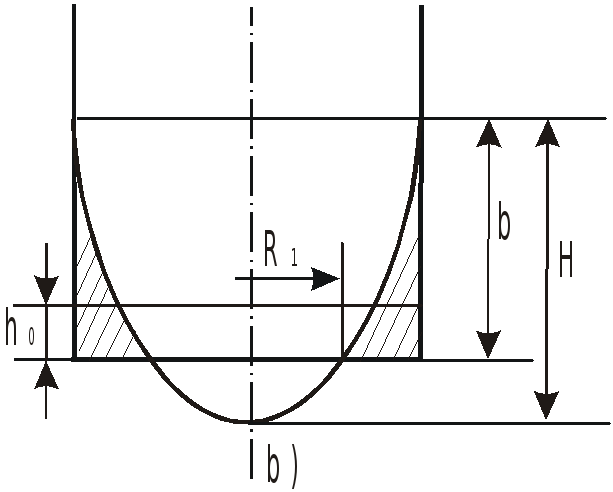

состоянии покоя ![]() .
.
При вращении в случае а) ![]() ,
,
где
![]()
– объем параболоида вращения, равный
![]() .
.
В случае b) ![]() .
.
Осевая сила давления жидкости на стенку
![]() ,
,
где
![]()
– объем тела давления, заключенный между
стенкой, свободной поверхностью с
![]()
и вертикальными образующими.
Когда свободная поверхность жидкости
отсутствует, положение поверхности
уровня определяется из условия, что она
проходит через точку жидкости, давление
в которой равно атмосферному.
Равномерное вращение цилиндрического сосуда вокруг оси, не совпадающей с вертикалью.
При вращении сосуда вокруг наклонной
или горизонтальной оси поле массовых
сил неоднородно и несимметрично
относительно оси вращения.
При больших угловых скоростях сила
тяжести пренебрежимо мала по сравнению
с центробежной силой, и в расчетах ею
можно пренебречь. В условиях невесомости
единственной силой при вращении сосуда
будет также центробежная сила.
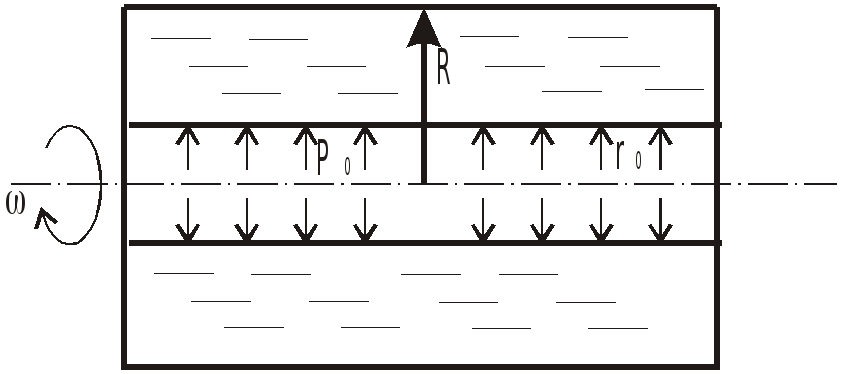
В
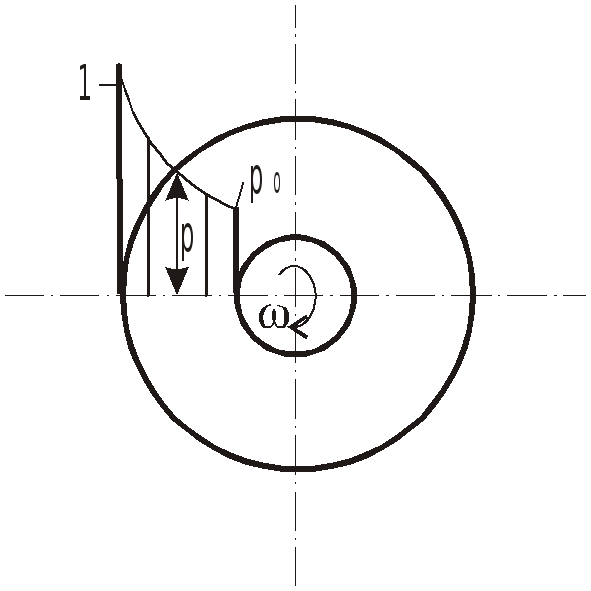
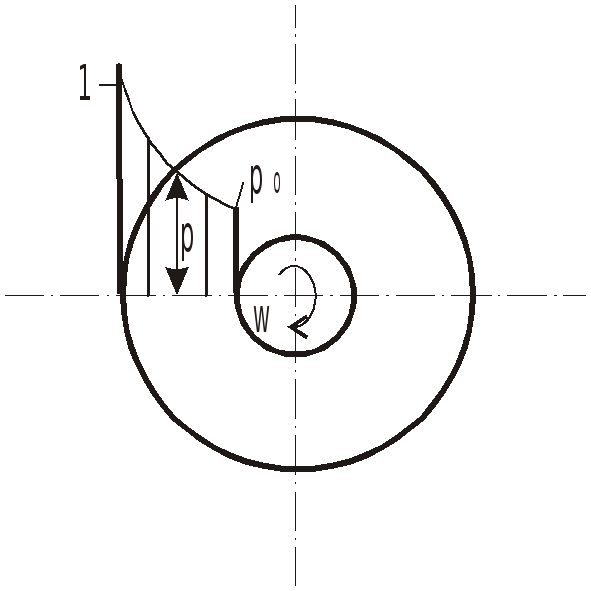
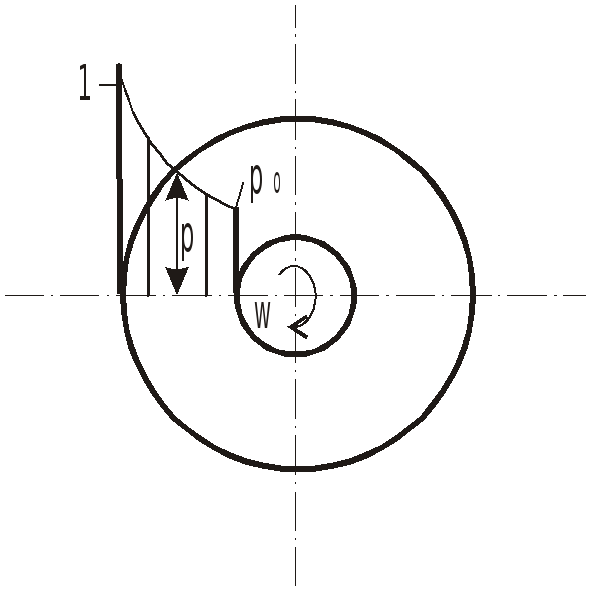
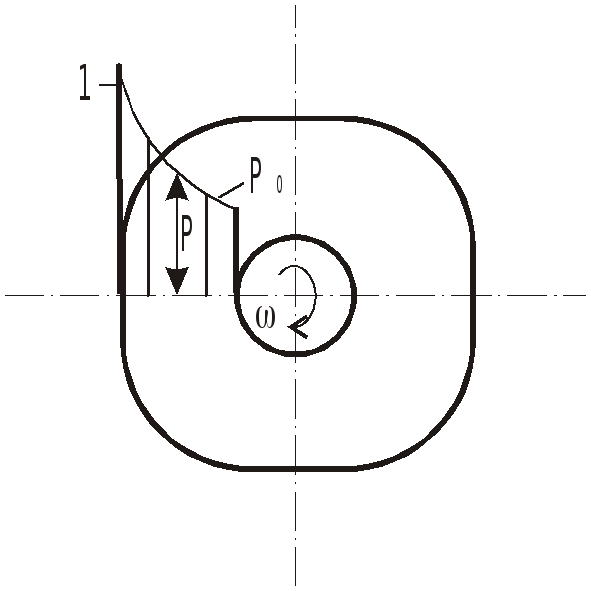
этих случаях поверхности уровня
представляют собой концентрические
цилиндры с осями вращения, совпадающими
с осью вращения сосуда (рис…), и закон
распределения давления имеет вид:
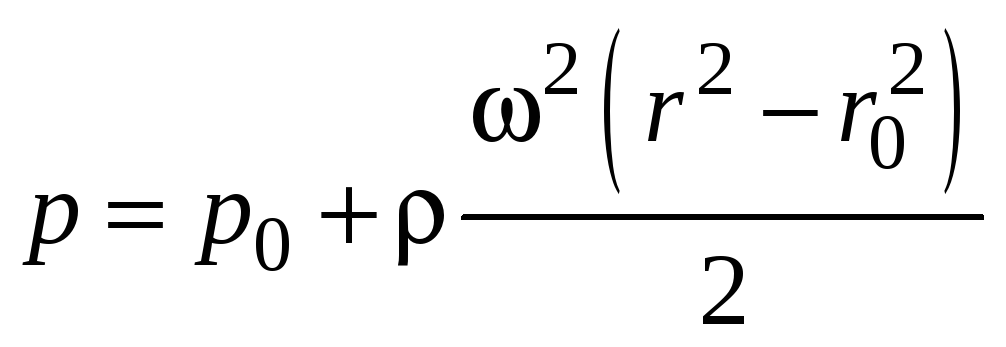
Задача 6.1
Ц
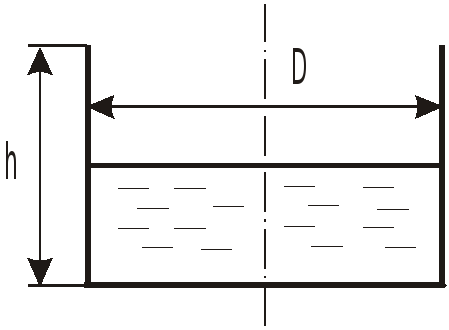
илиндрический сосуд высотой
![]()
и диаметром
![]() ,
,
заполненный жидкостью до половины,
начинает вращаться.
Определить максимальную угловую
скорость, при которой жидкость не будет
выливаться из сосуда.Найти силу, действующую на дно сосуда.
Дано:
![]()
;
![]() .
.
Решение:
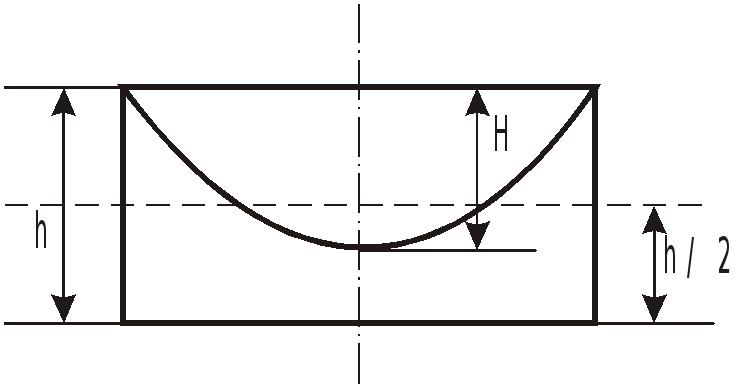
Определим положение вершины параболоида
вращения из условия равенства объемов
жидкости в покое и при вращении:
![]() ,
,
откуда ![]() .
.
Объем параболоида вращения
![]() ,
,
таким образом получаем
![]()
– параболоид вершиной коснулся дна,
откуда
![]() .
.
Н
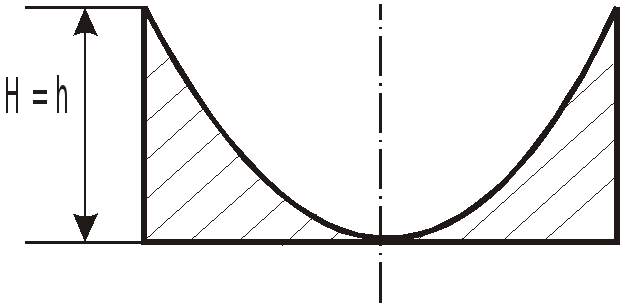
а дно сосуда действует сила,
направленная вертикально вниз и равная
весу тела давления
![]()
![]()
![]() .
.
Задача 6.2
Ц
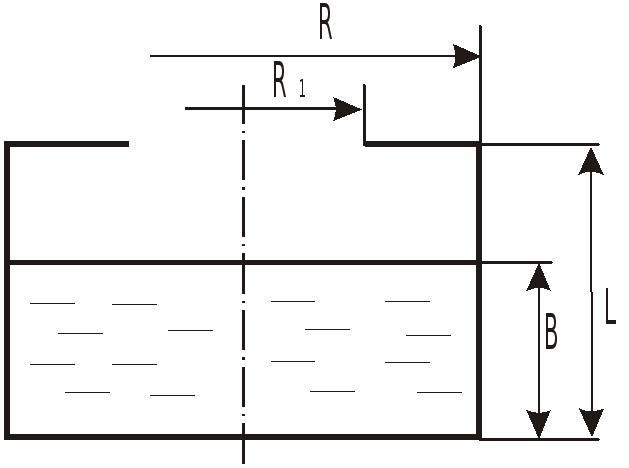
илиндрический сосуд высотой
![]()
и радиусом
![]() ,
,
имеющий отверстие в крышке радиусом
![]() ,
,
заполненный до высоты
![]()
жидкостью с плотностью
![]() ,
,
вращается вокруг вертикальной оси.
Определить угловую скорость сосуда,
при которой жидкость начнет выливаться
из него.Найти силу давления на верхнюю закраину
при этой угловой скорости.
Решение.
Ж
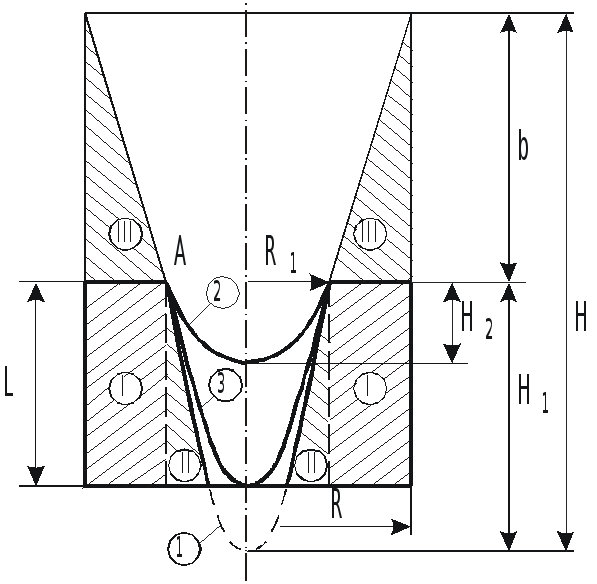
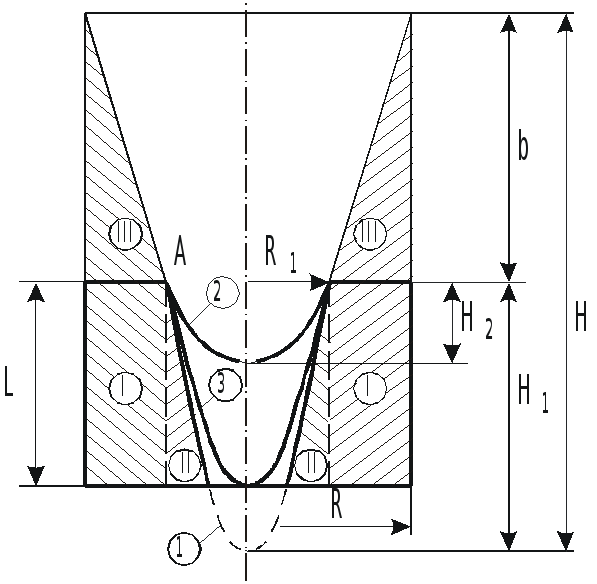
идкость начнет выливаться, когда
ее свободная поверхность по мере
увеличения угловой скорости достигнет
точки
![]() .
.
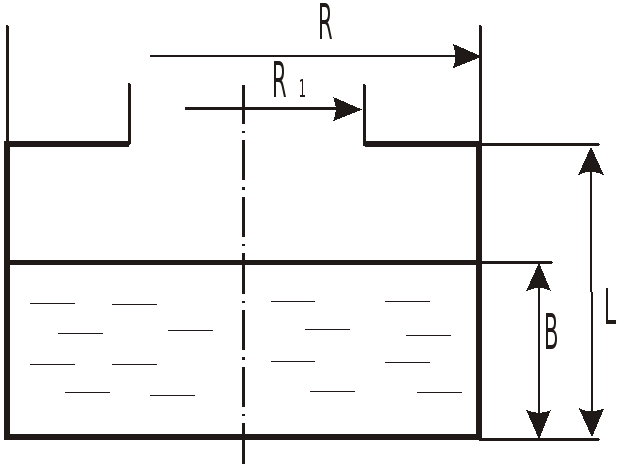
В зависимости от объема жидкости вершина
параболоида свободной поверхности
может занять одно из трех положений
(рис.).
В случае 3, когда параболоид касается
дна, объем жидкости в сосуде определяется
как разность между объемом цилиндра и
параболоида вращения:
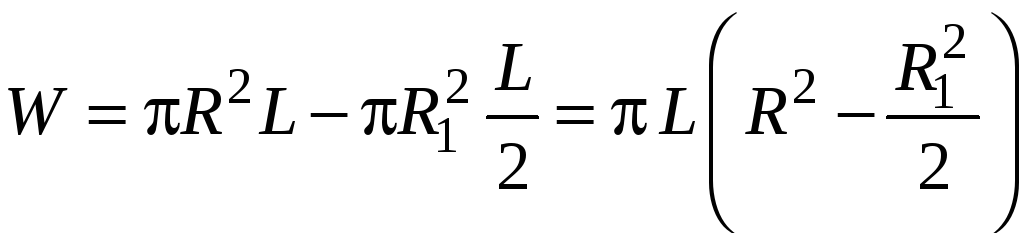 .
.
Первоначально жидкость заполняла сосуд
до высоты
![]() ,
,
и ее объем составлял:
![]() ,
,
тогда
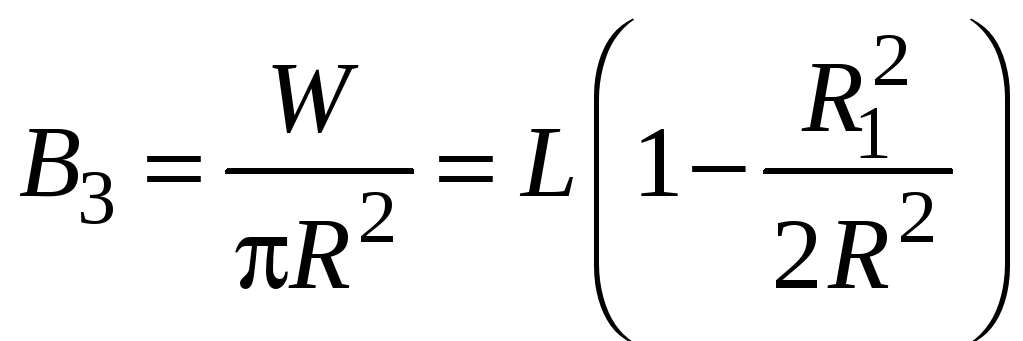 .
.
При
![]()
имеем случай 1, при
![]()
– случай 2.
Для случая 1
Из условия неизменности объема жидкости
в сосуде получаем:
![]() ;
;
Объемы: в покое тело I
тело II
Откуда:
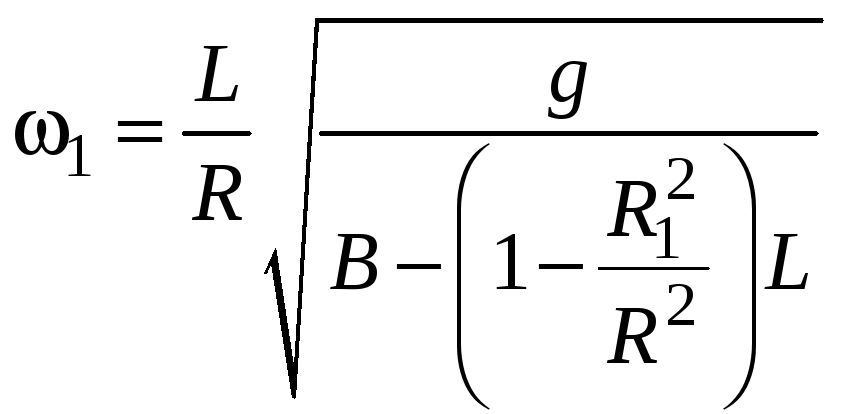 .
.
Для случая 2
![]() ,
,
учитывая, что
![]() ,
,
получим:
![]() .
.
При
![]()
выражения для угловой скорости во всех
трех случаях совпадают:
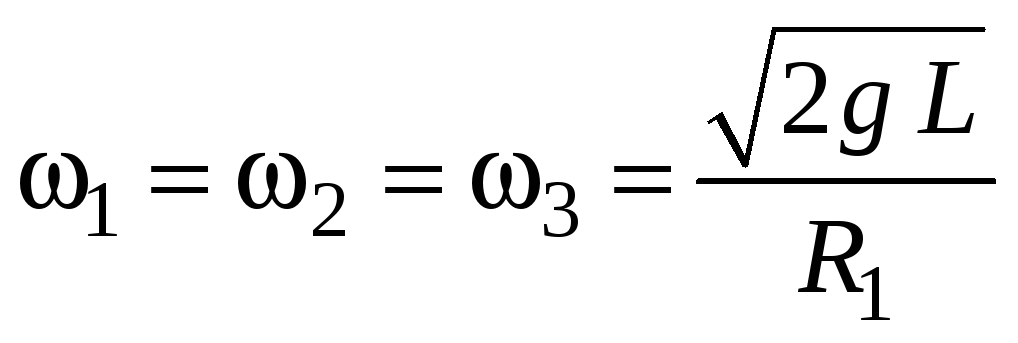 .
.
Сила давления на закраину равна весу
тела давления, заключенного между
стенкой, вертикальными образующими и
свободной поверхностью (тело III)
![]() учитывая,
учитывая,
что
![]() ,
,
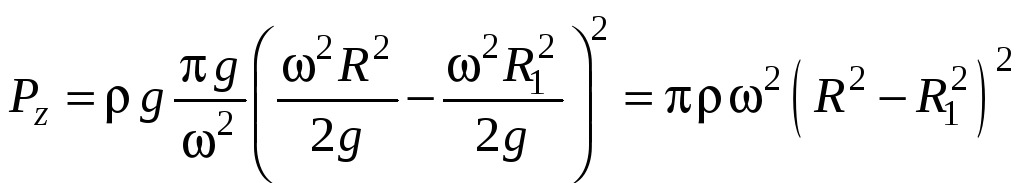 .
.
З
адача 6.3
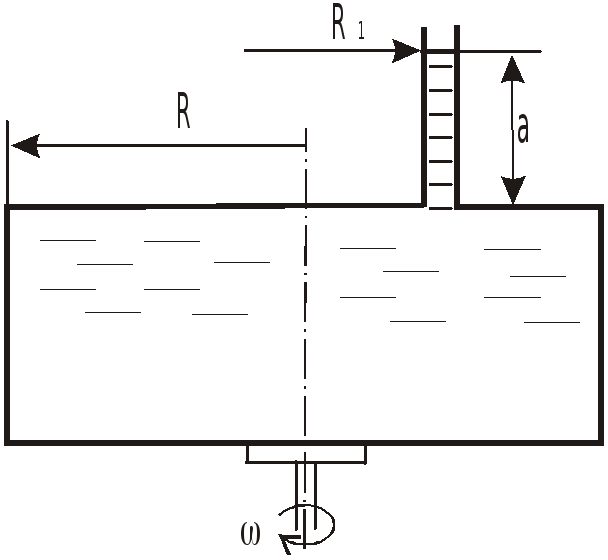
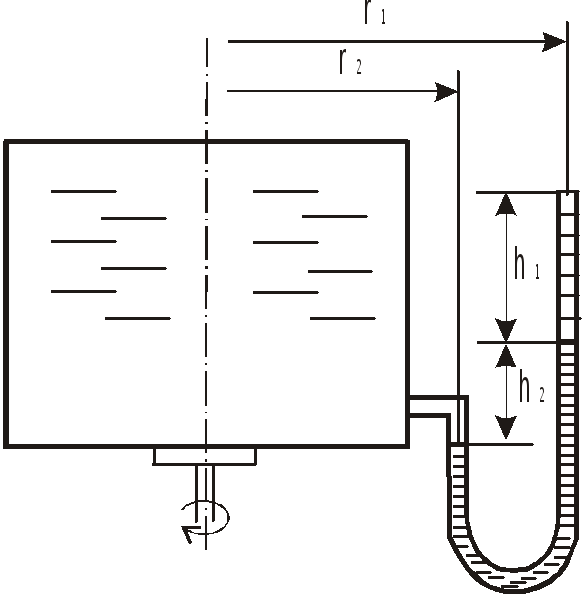
Цилиндрический сосуд радиусом
![]() ,
,
наполненный жидкостью с плотностью
![]()
до уровня а в открытой трубке,
установленной на расстоянии
![]()
от центра, вращается относительно
вертикальной оси.
Определить наибольшую угловую скорость
сосуда, до которой сохранится относительное
равновесие жидкости.Определить силу давления на крышку
сосуда при этой угловой скорости.
Решение.
З
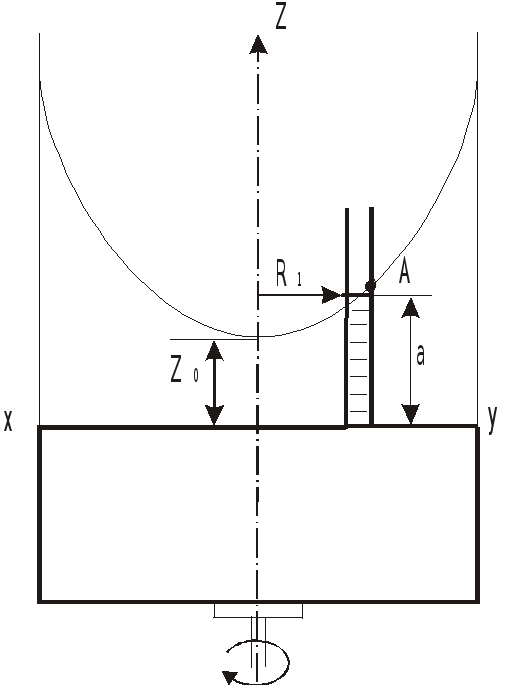
акон распределения избыточного
давления в жидкости:
![]() .
.
Начало координат примем в центре крышки.
Учитывая, что поверхность с
![]()
проходит через точку
![]()
с координатами
![]() и
и ![]() ,
,
найдем место расположения вершины
параболоида, образующего поверхность
с атмосферным давлением.
![]() ,
,
откуда
![]() ;
;
и закон распределения давления примет
вид:
![]() .
.
При возрастании
![]()
давление в центре понижается, но
возрастает по мере увеличения радиуса,
при этом в точке
![]()
давление остается равным атмосферному.
Если давление в центре крышки упадет
до давления насыщенных паров
![]() ,
,
произойдет разрыв сплошности жидкости,
и равновесие нарушается. Этому условию
соответствуют значения:
![]() .
.
Подставив это значение в уравнение
распределения давления по крышке, найдем
искомую угловую скорость
![]() :
:
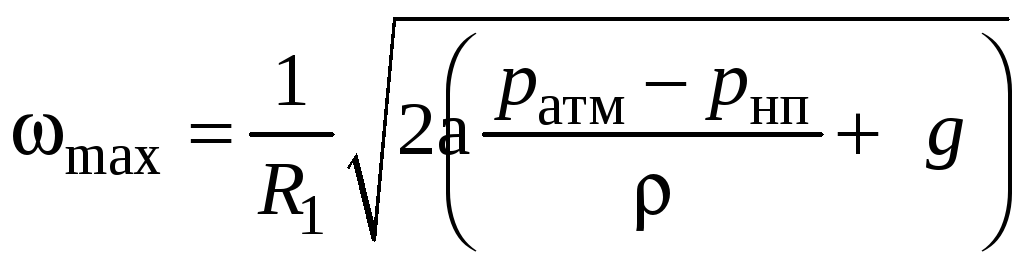 .
.
Сила давления на крышку равна весу тела
давления:
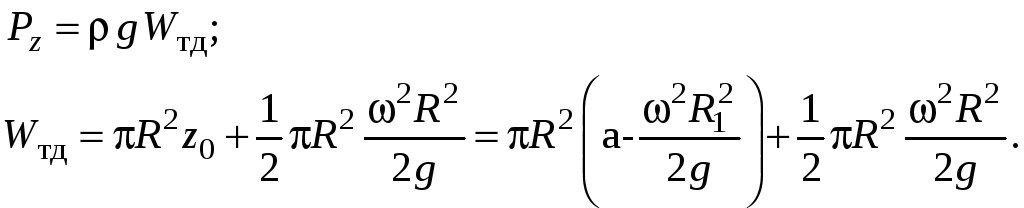
Задача 6.4
Ц
илиндрический сосуд, заполненный
водой, приведен во вращение с постоянной
угловой скоростью
![]() .
.
Найти наименьшее давление в воде,
заполняющей сосуд, по показанию ртутного
манометра, вращающегося вместе с
сосудом, если
 .
.При какой угловой скорости равновесие
жидкости в сосуде нарушается, если
разрыв жидкости происходит при вакууме
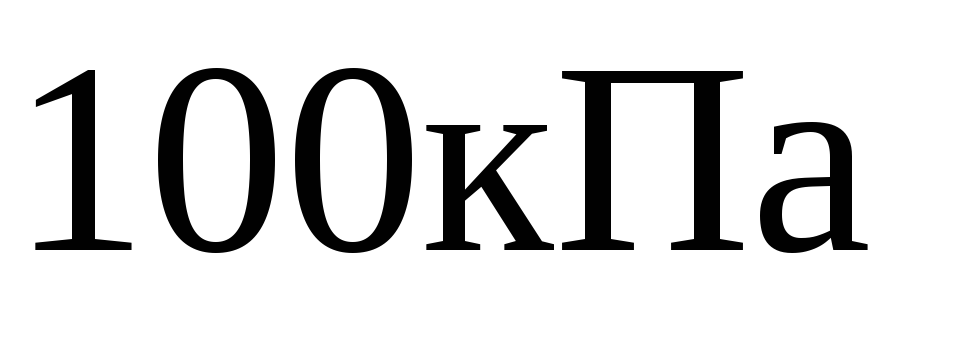 .
.
О
твет: Вакуум ![]() .
.
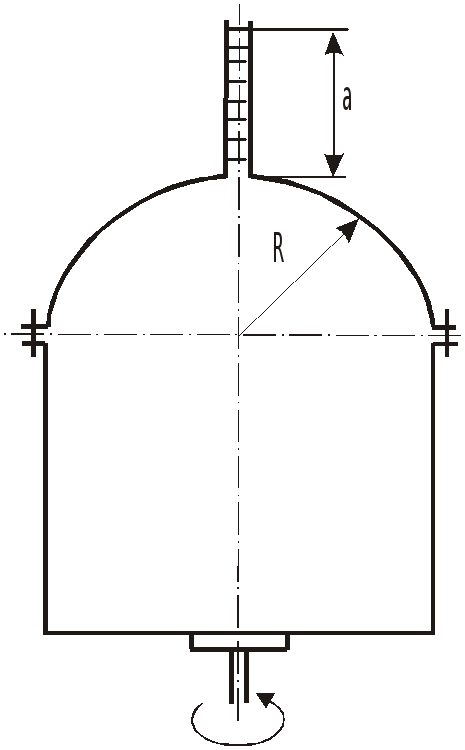
Задача 6.5
Цилиндрический сосуд, закрытый
полусферической крышкой радиусом
![]() ,
,
вращается с угловой скоростью
![]() .
.
В открытой трубке малого диаметра вода
поднялась на высоту
![]()
над центром крышки.
Определить силу, действующую на крышку.
Ответ: ![]() .
.
Задача 6.6
Цилиндрический сосуд, закрытый крышкой,
частично заполненный водой, вращается
вокруг вертикальной оси с постоянной
угловой скоростью. Пространство над
свободной поверхностью сообщается с
атмосферой. Как изменится сила, действующая
на крышку, если в сосуд поместить ртуть?
Задача 6.7 Цилиндрический сосуд.
Ц
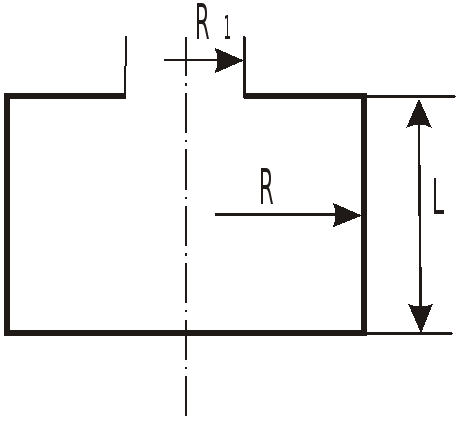
илиндрический сосуд высотой
![]()
и радиусом
![]() ,
,
имеющий в крышке отверстие радиусом
![]()
вращается вокруг вертикальной оси.
До какой высоты можно заполнить сосуд,
чтобы ни при какой угловой скорости
жидкость из него не вытекала.Какая часть объема сосуда может быть
заполнена, чтобы дно сосуда не оголялось,
и жидкость не вытекала.При каком числе n
оборотов/мин это возможно?
Ответ: .
З
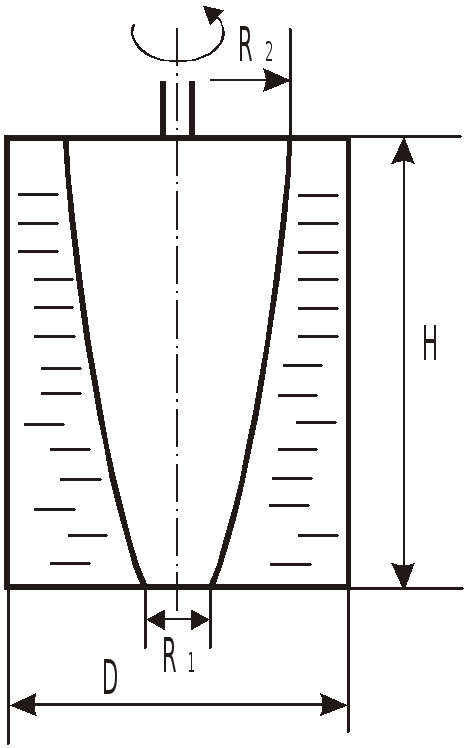
адача 6.8
При отливке цилиндрической полой
заготовки во вращающейся относительно
вертикальной оси форме из-за действия
сил тяжести нижний внутренний радиус
отливки
![]()
будет меньше внутреннего радиуса
![]() .
.
Определить их разность, если высота
отливки
![]() ,
,
угловая скорость вращения
![]() .
.
Диаметр формы
![]() ,
,
и она в начальный момент заполнена на
30% своего объема.
Ответ: ![]() .
.
Соседние файлы в пр?
