Равновесие жидкости в движущемся сосуде

В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать
различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.
1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции.
Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле
p = p0 + ρ·(g·z ± a·x),
Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:
g·z = ± a·x
или
z/x = tg α = ± a/g,
где α – угол наклона свободной поверхности жидкости к горизонту.
Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l)
высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.
Если сосуд движется равномерно (а = 0), уравнение приводим к виду:
p = p0 + ρ·g·z = p0·γ
В этом случае поверхность равного давления представляет горизонтальную плоскость.
2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.
Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:
p = p0 + γ·((ω2·r2)/(2·g) – z)
Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:
z = (ω2·r2)/(2·g) = u2/(2·g),
где окружная скорость u = ω·r (r — радиус вращения точки).
Высота параболоида вращения:
h = ω2·r20/(2·g),
где r0 – радиус цилиндрического сосуда.
Сила давления жидкости на дно сосуда:
P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),
где h0 – начальная глубина жидкости в сосуде до момента его вращения.
Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).
3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.
В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.
Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).

При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).
Распределение давления по глубине жидкости определяется выражением:
p = p0 + γ·ω2·(r2 – r20)/(2·g)
где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.
Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.
Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в.
Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Источник
Содержание:
- Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси.
Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси
Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси. В состоянии равновесия в движущемся сосуде жидкость движется вместе со всем контейнером. То есть, жидкость находится в относительном состоянии покоя. Рассмотрим цилиндрический контейнер радиусом H (рис. 2.9), заполненный до определенного уровня жидкостью плотностью p и вращающийся с постоянной угловой скоростью относительно вертикальной оси.
Через некоторое время после начала вращения сосуда жидкость под действием трения вращается с той же скоростью, что и сосуд. Равновесие жидкости устанавливается для сосуда, другими словами, для неинерциальных систем координат x, y, r, которые вращаются вместе с сосудом. При написании уравнений равновесия в неинерциальных системах необходимо ввести силу подвижной инерции в число рабочих forces.
В абсолютно покоящейся жидкости (сосуд неподвижен) действующей массовой силой (в поле сил тяжести) является только сила тяжести.
Людмила Фирмаль
- В рассматриваемом случае такая сила направлена вдоль радиуса и равна & M (центробежная сила равна n2g элементарной массы AM, которая вращается на расстоянии r от вертикали axis. In помимо центробежной силы, гравитация DM ^действует на любую частицу AM-это: за счет силы тяжести ^ = ° ;=°; ПГХ = —§; От портативной инерции п *. =<sup class=»reg»>®</sup>ГХ Риш-0)2 в> пр%= 0、 Где*и y-горизонтальные координаты произвольно выбранной точки А в жидкости. Рассмотрим 2 вопроса здесь. 39.
Форма поверхности одинакового давления. Используйте уравнение поверхности равного давления (2.10)’ Rhyh + ру ю + Rghyg-0 Когда вы назначаете ему выражения Px, Py и Pr, вы находите co2 x yx + co2 yy-diig-0. После интеграции、 гг-(* 2 + У2) §Р= С Или Х2 + У2-Г2.、 СО2-Р2 / 2 §р= с(2.23) Как видно из (2.23), поверхность равного давления в этом случае представляет собой семейство совпадающих 1-вращающихся параболоидов с вертикальной осью. Различные значения константы C соответствуют различным параболам одинакового давления.
- Свободная поверхность это также поверхность, на которой давление во всех точках равно давлению, равному внешнему давлению p0. Найти значение любой константы c параболоида свободной поверхности. Х-0; У = 0; РСВ = Р0.Если подставить эти координаты в Формулу (2.23), то: Ц0 = § 0. Уравнения свободной поверхности * С ш-Р0 = ^ (*2 +! 2. ) 2-й. Или Огнестрел-20 = СО2 Г2 / 2Д, (2.24) Частицы жидкости, находящиеся в относительном стационарном состоянии во вращающемся сосуде на расстоянии радиуса r от оси вращения, имеют линейную скорость u-(π.
Высота, на которой точка свободной поверхности выше вершины параболоида(например、 Б = РК-Р0 = СО2 Р2 /2§= С2 / 2С (2.25) 1 матч-фигура, которая будет объединена при наложении. 40. 20 ордината вершины параболоида свободной поверхности при заданной угловой скорости зависит от количества жидкости в сосуде. Если перед вращением сосуда уровень жидкости был установлен на горизонтальную и высоту H, то объем жидкости был равен 2N2H.
Законы относительного равновесия жидкости находят широкое применение в промышленности, а именно, в измерительной технике (жидкостные тахометры), в металлургии (центробежное литье) и других областях техники.
Людмила Фирмаль
- При вращении сосуда свободная поверхность становится параболой, форма объема жидкости изменяется, а величина при p = const{остается неизменной: | (Р0 +(r212d О2 ) О После интеграции、 Ч ■= рН + П2 К2 / 4Д Или Р0 = я-п * д * / 4#. Предполагая, что 20 = 0, мы знаем угловую скорость a, когда свободная поверхность жидкости касается дна контейнера. w = 2 Уды / я. Закон распределения давления. Используя дифференциальное уравнение жидкостных равновесий (2.5) и подставляя в него проекцию распределения плотности массовых сил, он выглядит следующим образом: гг = pY2(xc1x + ыыы) Сделай сам.
После интегрирования уравнения(2.26)、 / ? п(w2g72-ДГ)+ КБ(2.27) Если подставить координаты r = 0, r-r0 и давление p = p0 в уравнение (2.27), то получим Cp. С1! = Р0-Р (н0)= Р0 + rd0 Подставляя найденные значения C1 в(2.27), получаем 2r2 / 2d = H ’позволяет переписать любую точку в виде (2.28). Здесь k-глубина погружения точки под свободную поверхность, то есть вертикальное расстояние от свободной параболы до точки задачи. Поэтому в жидкости, которая неподвижна в равномерно вращающемся сосуде, вертикальное давление распределяется по закону гидростатического давления.
Смотрите также:
Задачи по гидравлике
Возможно эти страницы вам будут полезны:
- Равновесие однородной несжимаемой жидкости относительно земли.
- Геометрическая интерпретация основного уравнения гидростатики.
- Силы давления покоящейся жидкости на горизонтальные и наклонные плоские площадки (стенки).
- Силы давления покоящейся жидкости на цилиндрические стенки.
Источник
из “Прикладные задачи по гидравлике
“
При равновесии в движущемся сосуде жидкость, заполняющая сосуд, движется вместе с ним как твердое тело. В зависимости от характера действующих массовых сил в жидкости поверхность равного давления, как и свободная поверхность, может принимать различную форму. Рассмотрим некоторые случаи равновесия жидкости в движущихся сосудах.
[c.99]
В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерщ1и.
[c.99]
Рс Р8 С где h расстояние от точки С до пьезометрической плоскости.
[c.100]
Силы давления жидкости на плоские стенки в рассматриваемом случае равновесия благодаря однородности поля массовых сил определяются зависимостями, которые используются в случае равновесия жидкости в неподвижном сосуде [2]. Координаты центра давления действующих сил зависят от величины и направления ускорения а и определяются по формулам, приведенным в [2].
[c.100]
В выражениях (6.1)- (6.7) ускорение а принимается с учетом знака.
[c.101]
Изложенные выше замечания к формуле (6.4) справедливы и для формул (6.5) – (6.7). Также справедливы в данном случае и замечания по определению сил давления жидкости на плоские стенки и координат центра давления.
[c.101]
Формула (6.18) применима и для сосудов с избыточным (Ро PmmJ или вакуумметрическим давлением (ро р щ) над жидкостью, если отсчитывать координаты Z и X от пьезометрической плоскости, т.е. от поверхности уровня, давление в точках которого равно атмосферному.
[c.103]
Поверхность уровня представляет собой параболоид вращения, ось которого совпадает с осью вращения сосуда (рис. 6.6).
[c.103]
Из уравнения (6.20) следует параболический закон распределения давления по радиусу (рис. 6.6).
[c.104]
Рассмотрим случай, когда центробежные силы велики по сравнению с силой тяжести жидкости и последней можно в расчетах пренебречь, т.е. при условии g.
[c.105]
Закон распределения давления (6.26) по радиусу является параболическим. Эпюры давления представлены на рис. 6.9, в.
[c.105]
Если сила тяжести мала по сравнению с центробежной, то формула (6.26) может применяться при любом расположении оси вращения сосуда.
[c.105]
Задача 6.2. Цистерна, заполненная нефтью (относительная плотность 5 = 0,9), движется на спуске с уклоном i = 0,105. Диаметр горловины d = 0,7 м, а высота горловины над поверхностью нефти в неподвижной цистерне на горизонтальной плоскости (рис. 6.11)дй = 0,2 м. Определить ускорение, при котором нефть поднимется до передней кромки горловины.
[c.106]
На рис. 6.12 обозначено 1 – свободная поверхность нефти при движении цистерны с замедлением 2 – горизонтальная плоскость 3 – плоскость движения цистерны.
[c.107]
Нефть поднимется до передней кромки горловины при торможении цистерны с ускорением а = -4,52 м/с.
[c.107]
Задача 6.3. Цистерна, заполненная дизельным топливом, движется со скоростью U = 36 км/ч по горизонтальному закруглению радиусом R = 300 м. Определить угол наклона свободной поверхности дизельного топлива (рис. 6.13).
[c.107]
Знак (-) указывает на то, что уровень нефти понижается у боковой noBqjxHO TH цистерны со стороны центра закругления.
[c.107]
Задача 6.4. Циливдрический сосуд диаметром D, =300 мм и высотой L = 250 мм, имеющий в верхней крышке центральное отверстие диаметром 1 2 = 200 мм, заполнен нефтью плотностью р = 900 кг/м до высоты 5 = 180 мм (рис. 6.14). Определить угловую скорость сосуда, при которой жидкость начнет выливаться из него, и силу давления на верхнюю крышку при этой угловой скорости.
[c.108]
Решение. Жидкость начнет выливаться из сосуда, когда ее свободная поверхность по мере увеличения угловой скорости достигнет кромки отверстия в верхней крьппке. При этом вершина параболоида свободной поверхности в зависимости от объема жидкости в сосуде может расположиться ниже или выше дна сосуда.
[c.108]
Указание. В сосуде не останется жидкости, когда свободная поверхность жидкости коснется стенки сосуда у его дна, и вектор сум.марной массовой силы, действующей на последнюю частицу жидкости в этой точке, будет нормальным к стенке.
[c.112]
Вернуться к основной статье
Источник
Существуют два вида равновесия — абсолютное и относительное. Абсолютное равновесие — равновесие жидкости относительно Земли, т.е. когда на жидкость действует только сила тяжести. Относительное равновесие жидкости — это ее равновесие по отношению к сосуду, перемещающемуся прямолинейно и равноускоренно относительно Земли или вращающемуся относительно собственной оси с постоянной угловой скоростью.
Рассмотрим два характерных случая относительного равновесия: прямолинейное равноускоренное движение сосуда с жидкостью и равномерное вращательное движение сосуда относительно собственной оси.
Относительное равновесие жидкости в сосуде, движущемся прямолинейно с постоянным ускорением. Цистерна с жидкостью (рис. 1.18) движется равномерно, ускоренно в направлении оси Хс ускорением +а.
Рис. 1.18. Схема относительного покоя жидкости в движущемся резервуаре
Пунктиром показано положение жидкости при абсолютном равновесии. Но в данном случае на жидкость помимо ускорения силы тяжести действует ускорение силы инерции, т.е. У= О, Х= —a, Z = —g. Проинтегрируем уравнения поверхности равного давления и уравнение изменения давления. Из первого уравнения имеем
Для* = 0,z = ZmnC = zm имеем
Отсюда уравнение (1.21) есть уравнение прямыхлиний, наклоненных к оси X под углом а = arctg . Учитывая, что эта линия есть
8 )
проекция поверхностей равного давления, представляющих собой семейство плоскостей, наклоненных под углом а к оси X, нормально расположенных перпендикулярно вектору результирующего ускорения у, модуль которого j = yjg2 +а2.
В случае движения сосуда в том же направлении, но с торможением, т.е. ускорение сосуда — а, тогда величина Xравна ускорению движения, взятому с обратным знаком, т.е. в этом случае X = +а
~ о „ ^ а
и Z =—х + С и а = arctg—.
88
зо
Проинтегрируем теперь для данного случая относительного равновесия уравнение изменения давления:
Это уравнение определяет давление, например, в точке А. Определим давление в соответствии с этой формулой в точке А лежащей на одной вертикали с точкой А, принадлежащей свободной поверхности Z = Z0,P =р0:
Составим разность этих уравнений
т.е. давление в этом случае выражается той же формулой, что и в случае абсолютного равновесия, но значение (z0 — z) измеряется до свободной поверхности непосредственно над точкой, в которой определяется давление.
Относительное равновесие жидкости в сосуде, равномерно вращающемся вокруг вертикальной оси z с угловой скоростью со. Совместим ось Z с осью вращения сосуда (рис. 1.19) и систему координат свяжем с вращающимся сосудом.
В рассматриваемом случае на частицы жидкости действуют следующие массовые силы: сила тяжести с ускорениемg; центробежная сила инерции с ускорением jr = со2 г, где г — расстояние от данной точки до оси вращения. Ускорение действует в горизонтальной плоскости. Его проекции
гдехиу—координаты рассматриваемой точки А. По-прежнему Z= —g. Найдем уравнение свободной поверхности вращающейся жидкости, используя уравнение поверхности равных давлений (1.6):
Рис. 1.19. Схема относительного покоя жидкости во вращающемся относительно своей вертикальной оси резервуаре
Это уравнение параболоида вращения, который и представляет поверхность равных давлений. Постоянную интегрирования определим из условия г = 0, когда z = zm и —С = zm, тогда
Придавая ^различные значения, получим семейство эквидистантных поверхностей в виде параболоидов вращения. При Zm = Z™получим уравнение свободной поверхности:
Рассмотрим выражение для изменения давления:
Постоянную интегрирования определим, написав условие для точки свободной поверхности, лежащей на оси вращения: ра6с = р0;
Г = 0; z=$, тогда ^- = -г0″+С, С=^-+го”.
У У
Подставляя это значение С в выражение (1.22), получим
т OoV
но значение z0 4—-— = z0, тогда ра6с = р0 + уп, т.е. давление опять выражается той же формулой, что и в случае абсолютного равновесия. При этом глубина h замеряется отданной точки до точки на свободной поверхности, лежащей на одной вертикали.
Источник

вующая массовая сила всегда действует нормально к поверхности уровня. Выбирая систему координат, жестко связанную со стенками сосуда, приходим к статической задаче, основой для решения которой служит диф-
ференциальное уравнение равновесия жидкости:
dp = ρ(Xdx + Ydy + Zdz), | (2.1) |
где x, y, z – координаты точек жидкости в системе отсчета, связанной с сосудом; p – давление в жидкости; ρ – плотность жидкости;
X, Y, Z – проекции единичной массовой силы на координатные оси.
Для определения формы поверхности уровня и характера распределения давления в этом сосуде следует в число действующих массовых сил включить также силы инерции.
Существуют два состояния относительного покоя жидкости:
–в сосуде, движущемся прямолинейно и равноускоренно;
–в сосуде, равномерно вращающемся вокруг вертикальной оси.
Сосуд с жидкостью движется с ускорением a вдоль прямой, накло-
z
z0
0(y)
α
Рис. 2.1. Относительное равновесие жидкости при прямолинейном равноускоренном движении сосуда
ненной к горизонту под углом α (рис. 2.1).
К массовым силам наряду с силой тяжести в данном случае относится еще и сила инерции j = – a, направленная противоположно ускорению сосуда. В системе координат (рис. 2.1) проекции единичных массовых сил будут равны
X = j – g sin α ; Y = 0 ; Z = – g cos α.
Подставляя эти выражения в уравнение равновесия (2.1), получаем
dp = ρ [(j – g sin α)dx – g cos α dz], | (2.2) |
а после интегрирования
p = ρ (j – g sin α) x – ρ g cos αz + C,
20
z − z0 =
где С – постоянная интегрирования, определяемая из граничных условий на свободной поверхности при x = 0, z = z0 и p = p0.
После подстановки граничных условий получаем закон распределения давления:
p = р0+ρ(j – g sin α) x +ρ g cos α (z0 – z). (2.3)
Так как на поверхности уровня давление одинаково в любой ее точке, полагая в уравнении (2.2) p = const, получаем уравнение поверхностей уровня
ρ( j – g sin α) x – ρ g cos α z + C1 = 0. | (2.4) |
Уравнение (2.4) дает семейство плоскостей, параллельных оси Y. Одной из этих плоскостей является свободная поверхность.
Подставляя в формулу (2.4) граничные условия x = 0 и z = z0, нахо-
дим
C1 = ρ g z0 cos α.
Уравнение свободной поверхности имеет вид
j − g sinα x , (2.5) g cosα
где | j − g sinα | = tgθ . |
g cosα | ||
2.3. Равновесие жидкости в цилиндрическом сосуде, равномерно вращающемся вокруг вертикальной оси
Равновесие жидкости в сосуде, вращающемся вокруг вертикальной оси, реализуется лишь при постоянной угловой скорости вращения ω = const (рис. 2.2).
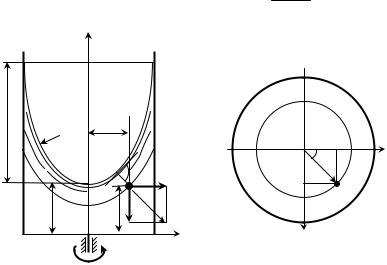
По истечении достаточного времени после начала вращения жидкость приобретает ту же скорость вращения, что и сосуд, а свободная поверхность ее видоизменяется: в центральной части уровень жидкости понизится, у стенок – повысится и вся свободная поверхность станет некоторой поверхностью вращения (рис.2.2, а). На жидкость в этом случае будут действовать две массовые силы: сила тяжести и центробежная сила, кото-
рые, будучи отнесенными к единице массы, соответственно равны g и ω²r. При проецировании на оси координат равнодействующей массовых
сил (рис.2.2, б) получим выражения
X = ω2 r cos α= ω2 x ;Y = ω2 r sin α = ω2 y ; Z = – g.
Подставляя эти выражения в уравнение (2.1), получаем dp = ρ(ω2xdx +ω2ydy – gdz),
или
dp = ρ(ω2rdr – g dz).
21
После интегрирования находим | |||
p =с | щ2 r 2 | −сg z +C . | (2.6) |
2 | |||
Подставляя в уравнение (2.6) граничные условия r = 0, z = z0 и p = p0, | |||
находим постоянную интегрирования | |||
C = р0 + ρ g z0. | |||
Тогдазаконраспределениядавленияможновыразитьформулой | |||
p = p0 +сщ2r2 +сg(z0 − z) , | (2.7) | ||
2 | |||
т. е. в этом случае также справедлив линейный закон распределения давления по глубине. Изменение давления по радиусу подчиняется параболическому закону. Полагая p = const, из выражения (2.6) получим уравнение поверхностей уровня:
p =с | щ2 r 2 | −сgz +C1 . | (2.8) | |
2 | ||||
z | ||||
H | r | |||
p0 | O | |||
ω2r | r α y | x | ||
x | ||||
g | j | |||
z | ||||
O | x | y | ||
ω=const | ||||
а | б | |||
Рис. 2.2. Относительное равновесие жидкости в равномерно | ||||
вращающемся цилиндрическом сосуде | ||||
Эти поверхности уровня представляют собой параболоиды вращения. Одним из таких параболоидов является свободная поверхность жидкости.
Так как в вершине параболоида свободной поверхности r = 0, z = z0,
C1 = ρg z0 ,то уравнение свободной поверхности примет вид | ||||||
z − z0 | = | щ2 r 2 | . | (2.9) | ||
2g | ||||||
Зависимость | щ2 r 2 | |||||
z − z0 | = | h = | (2.10) | |||
2g | ||||||
при постоянном радиусе (r = const) устанавливает связь между величиной возвышения h любой точки, расположенной на свободной поверхности
над точкой, лежащей на оси вращения, и угловой скоростью ω. Она позволяет определить число оборотов цилиндра, если известно превышение h , что и используется при конструировании жидкостных тахометров, с помо-
22
Источник
