Равновесие жидкости во вращающемся сосуде
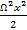
Рассмотрим случай, когда на жидкость, помимо объемных сил тяжести, действует еще другая система объемных сил, например, система центробежных сил инерции.
Возьмем круглоцилиндрический сосуд, наполненный жидкостью, причем будем считать, что этот сосуд вращается вокруг своей вертикальной оси равномерно, т. е. с постоянной угловой скоростью (рис. 2-14). Благодаря силам трения стенки вращающегося сосуда будут вначале увлекать за собой жидкость, а по истечении некоторого времени вся жидкость начнет вращаться вместе с сосудом с той же угловой скоростью Ω, находясь по отношению к стенкам сосуда в покое. Силы трения при этом внутри жидкости, а также между жидкостью, стенками сосуда и его дном, будут отсутствовать.
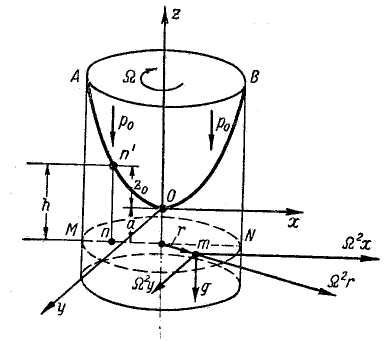
Рис. 2-14. Цилиндрический сосуд, вращающийся относительно вертикальной оси Oz
АОВ — свободная поверхность жидкости
Если оси координат, расположенные, как показано на чертеже, будем считать скрепленными с вращающимся сосудом, то по отношению к таким вращающимся осям координат жидкость также будет находиться в покое. Поэтому для исследования вращающейся жидкости при указанных подвижных осях координат могут быть применены известные уравнения Эйлера (2-14).
В эти уравнения входит объемная сила , действующая на единицу массы жидкости. В данном случае сила будет слагаться из двух сил: силы тяжести и центробежной силы.
С тем чтобы найти проекцию центробежной силы на оси координат, наметим внутри жидкости точку т и выделим у нее элементарную массу жидкости δM. Масса δM будет вращаться вокруг оси сосуда, двигаясь по окружности, имеющей радиус r и лежащей в плоскости, нормальной к оси сосуда. Центробежная сила, действующая на данную массу, будет
I’= , (2-62)
где υ – скорость движения массы δM по окружности радиуса r.
Центробежная сила, отнесенная к единице массы жидкости, сосредоточенной в точке т,
I = = Ω2r. (2-63)
Эта сила, так же как и сила I’, направлена по радиусу от оси сосуда наружу. Проекции силы I (отнесенной к единице м- ассы) на оси координат
Ix = Ω2rcos(r,x) = Ω2x
Iy = Ω2rcos(r,y) = Ω2y
Iz = 0 (2-64)
Проекции объемной силы тяжести, отнесенной к единице массы, выражаются зависимостью (2-28). Складывая объемные силы тяжести и объемные центробежные силы, отнесенные к единице массы, получаем
= 0 +Ω2x = Ω2x;
= 0 + Ω2y = Ω2y;
= – (2-65)
Подставляя (2-65) в (2-17), найдем
dpA = ρ(Ω2xdx + Ω2ydy – , (2-66)
что после интегрирования дает
dpA = ρ( + – ) + C = (x2 + y2) – ρ C. (2-67)
Постоянную интегрирования С устанавливаем, написав (2-67) применительно к точке, находящейся в начале координат, для которой x = y = z =0; p = p0. Как видно,
C = p0 (2-68)
причем (2-67) перепишется в виде:
pA = p0 + (x2 +y2) – γz (2-69)
Это последнее уравнение и выражает закон распределения давления в рассматриваемой жидкости. Пользуясь таким уравнением, можно найти поверхности равного давления.
Действительно, уравнение поверхности, во всех точках которой давление pA = pi= const, запишется в виде
(x2 +y2) – γz = pi – p0. (2-70)
Уравнение (2-70) выражает поверхность, являющуюся параболоидом вращения (с вертикальной осью).
Свободная поверхность жидкости, характеризуемая постоянным давлением pi = p0, представляет собой также параболоид вращения; уравнение ее будет:
(x2 +y2) – γz = 0. (2-71)
Если учесть, что x2 + y2 = r2, то, решив (2-71) относительно z, получим следующее уравнение, по которому легко построить параболу АОВ, дающую свободную поверхность:
z0 = r2 (2-72)
где z0- ордината кривой АОВ.
Распределение давления в горизонтальной плоскости MN, лежащей ниже начала координат на величину a, можно найти, пользуясь (2-69):
pA = p0 + (x2 +y2) +γa = p0 + ρ r2+ γa = p0 + γ( r2+ a). (2-73)
Учитывая (2-72), получаем
pA = p0 + γ(a + z0) = p0 + γh (2-74)
где h = a +z0 показано на рис. 2-14.
Таким образом, давление в жидкости, находящейся внутри равномерно вращающегося сосуда, выражается зависимостью того же вида, что и для случая тяжелой покоящейся жидкости [см. (2-39)]; под величиной h здесь надо понимать только заглубление рассматриваемой точки под криволинейной свободной поверхностью.
Источник
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила Pu = mω2r, где r – расстояние частицы от оси вращения, а ω – угловая скорость вращения сосуда.
Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим
С другой стороны:
где z – координата рассматриваемой точки. Таким образом, получаем:
откуда
или после интегрирования
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь
После сокращений получим
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.
Вопрос №12. Поверхности равных давлений. Гидростатический закон распределения давления.
Поверхность, во всех точках которой значения гидростатического давления равны между собой, называют поверхностью равного давления или поверхностью уровня. На положение уровня свободной поверхности влияют силы тяжести и инерции.
Найдем величину равного давления Р по трем частным производным. При Р=const и р # 0 значение полного дифференциала dP=0 и, следовательно, уравнение поверхности жидкости равного давления имеет вид
Это уравнение называется уравнением поверхности жидкости равного или постоянного давления. Рассмотрим наиболее часто встречающиеся случаи.
Первый случай,когда на покоящуюся жидкость действует одна внешняя сила, сила тяжести, тогда , , (направление ускорения свободного падения не совпадает с положительным направлением оси Z). В этом случае исходное уравнение имеет вид
или
т. е. получаем поверхности равного давления, представляющие собой семейство горизонтальных плоскостей. Каждому значению Zсоответствует плоскость, точки которой имеют определенное постоянное значение давления. Свободная поверхность жидкости (для ограниченного объема), в данном случае—одна из плоскостей равного давления. Имеем в виду, что свободная поверхность — это поверхность на границе жидкой и газообразной сред. На свободную поверхность будет приложено постоянное давление равное атмосферному.
Сначала рассмотрим простейший случай покоя. Жидкость находится под действием силы тяжести. Это означает, что проекции ускорений на оси X и Y отсутствуют. Единственным ускорением является ускорение свободного падения g, т. е.:
, , .
Тогда полный дифференциал давления после подстановки в него ускорений примет вид:
.
После интегрирования этого выражения получим:
.
Постоянную интегрирования, равную
,
найдём, подставив параметры свободной поверхности и .
После подстановки этих значений в интеграл P будем иметь равенство:
Переписав это выражение в другом виде, получим
Если обозначить (Z0 – Z) через h, то приведённое равенство примет уже знакомый вид основного уравнения гидростатики
.
Из этого же равенства можно получить следующий вид
,
или
Последнее выражение часто называют основным законом гидростатики.
Вопрос №13. Виды движения жидкости. Измерение расхода жидкости, приборы
Проведём классификацию видов движения жидкости.
1. Классификация по признаку зависимости движения жидкости от времени.
1.1. Установившееся (стационарное).
1.2. Неустановившееся (нестационарное).
2. Классификация по признаку учёта сил трения, вязкости и теплопроводности.
2.1. Идеальная невязкая жидкость.
2.2. Вязкая жидкость.
3. Классификация по виду движения жидкости (поступательное или вращательного движение).
3.1. Безвихревое (потенциальное) (движение, когда вращение отсутствует).
3.2. Вихревое движение.
4. Классификация по характеру изменения плотности в потоке.
4.1. Несжимаемая (жидкость), r=const.
4.2. Сжимаемая (газ), r¹const.
5. Классификация по скорости и её отношению к скорости
расширяющихся возмущений (скорости звука).
5.1. Дозвуковое ( M<1) , где , V – скорость потока, а – скорость звука.
5.2. Трансзвуковое (М»1).
5.3. Сверхзвуковое (М>1).
5.4. Гиперзвуковое (М>>1).
6. Классификация по режиму течения.
6.1. Ламинарный режим, (Re£Reкр).
6.2. Турбулентный режим,(Re/Reкр).
7. Вид течения.
7.1. Свободное.
7.2. Вынужденное.
Дата добавления: 2015-04-18; просмотров: 117; Нарушение авторских прав
Источник
Содержание:
- Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси.
Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси
Равновесие жидкости в сосуде, равномерно вращающемся относительно вертикальной оси. В состоянии равновесия в движущемся сосуде жидкость движется вместе со всем контейнером. То есть, жидкость находится в относительном состоянии покоя. Рассмотрим цилиндрический контейнер радиусом H (рис. 2.9), заполненный до определенного уровня жидкостью плотностью p и вращающийся с постоянной угловой скоростью относительно вертикальной оси.
Через некоторое время после начала вращения сосуда жидкость под действием трения вращается с той же скоростью, что и сосуд. Равновесие жидкости устанавливается для сосуда, другими словами, для неинерциальных систем координат x, y, r, которые вращаются вместе с сосудом. При написании уравнений равновесия в неинерциальных системах необходимо ввести силу подвижной инерции в число рабочих forces.
В абсолютно покоящейся жидкости (сосуд неподвижен) действующей массовой силой (в поле сил тяжести) является только сила тяжести.
Людмила Фирмаль
- В рассматриваемом случае такая сила направлена вдоль радиуса и равна & M (центробежная сила равна n2g элементарной массы AM, которая вращается на расстоянии r от вертикали axis. In помимо центробежной силы, гравитация DM ^действует на любую частицу AM-это: за счет силы тяжести ^ = ° ;=°; ПГХ = —§; От портативной инерции п *. =<sup class=»reg»>®</sup>ГХ Риш-0)2 в> пр%= 0、 Где*и y-горизонтальные координаты произвольно выбранной точки А в жидкости. Рассмотрим 2 вопроса здесь. 39.
Форма поверхности одинакового давления. Используйте уравнение поверхности равного давления (2.10)’ Rhyh + ру ю + Rghyg-0 Когда вы назначаете ему выражения Px, Py и Pr, вы находите co2 x yx + co2 yy-diig-0. После интеграции、 гг-(* 2 + У2) §Р= С Или Х2 + У2-Г2.、 СО2-Р2 / 2 §р= с(2.23) Как видно из (2.23), поверхность равного давления в этом случае представляет собой семейство совпадающих 1-вращающихся параболоидов с вертикальной осью. Различные значения константы C соответствуют различным параболам одинакового давления.
- Свободная поверхность это также поверхность, на которой давление во всех точках равно давлению, равному внешнему давлению p0. Найти значение любой константы c параболоида свободной поверхности. Х-0; У = 0; РСВ = Р0.Если подставить эти координаты в Формулу (2.23), то: Ц0 = § 0. Уравнения свободной поверхности * С ш-Р0 = ^ (*2 +! 2. ) 2-й. Или Огнестрел-20 = СО2 Г2 / 2Д, (2.24) Частицы жидкости, находящиеся в относительном стационарном состоянии во вращающемся сосуде на расстоянии радиуса r от оси вращения, имеют линейную скорость u-(π.
Высота, на которой точка свободной поверхности выше вершины параболоида(например、 Б = РК-Р0 = СО2 Р2 /2§= С2 / 2С (2.25) 1 матч-фигура, которая будет объединена при наложении. 40. 20 ордината вершины параболоида свободной поверхности при заданной угловой скорости зависит от количества жидкости в сосуде. Если перед вращением сосуда уровень жидкости был установлен на горизонтальную и высоту H, то объем жидкости был равен 2N2H.
Законы относительного равновесия жидкости находят широкое применение в промышленности, а именно, в измерительной технике (жидкостные тахометры), в металлургии (центробежное литье) и других областях техники.
Людмила Фирмаль
- При вращении сосуда свободная поверхность становится параболой, форма объема жидкости изменяется, а величина при p = const{остается неизменной: | (Р0 +(r212d О2 ) О После интеграции、 Ч ■= рН + П2 К2 / 4Д Или Р0 = я-п * д * / 4#. Предполагая, что 20 = 0, мы знаем угловую скорость a, когда свободная поверхность жидкости касается дна контейнера. w = 2 Уды / я. Закон распределения давления. Используя дифференциальное уравнение жидкостных равновесий (2.5) и подставляя в него проекцию распределения плотности массовых сил, он выглядит следующим образом: гг = pY2(xc1x + ыыы) Сделай сам.
После интегрирования уравнения(2.26)、 / ? п(w2g72-ДГ)+ КБ(2.27) Если подставить координаты r = 0, r-r0 и давление p = p0 в уравнение (2.27), то получим Cp. С1! = Р0-Р (н0)= Р0 + rd0 Подставляя найденные значения C1 в(2.27), получаем 2r2 / 2d = H ’позволяет переписать любую точку в виде (2.28). Здесь k-глубина погружения точки под свободную поверхность, то есть вертикальное расстояние от свободной параболы до точки задачи. Поэтому в жидкости, которая неподвижна в равномерно вращающемся сосуде, вертикальное давление распределяется по закону гидростатического давления.
Смотрите также:
Задачи по гидравлике
Возможно эти страницы вам будут полезны:
- Равновесие однородной несжимаемой жидкости относительно земли.
- Геометрическая интерпретация основного уравнения гидростатики.
- Силы давления покоящейся жидкости на горизонтальные и наклонные плоские площадки (стенки).
- Силы давления покоящейся жидкости на цилиндрические стенки.
Источник
Рассмотрим случай,
когда на жидкость, помимо объемных сил
тяжести, действует еще другая система
объемных сил, например, система
центробежных сил инерции.
Возьмем
круглоцилиндрический сосуд, наполненный
жидкостью, причем будем считать, что
этот сосуд вращается вокруг своей
вертикальной оси равномерно, т. е. с
постоянной угловой скоростью (рис.
2-14). Благодаря силам трения стенки
вращающегося сосуда будут вначале
увлекать за собой жидкость, а по истечении
некоторого времени вся жидкость начнет
вращаться вместе с сосудом с той же
угловой скоростью Ω,
находясь по отношению к стенкам сосуда
в покое. Силы трения при этом внутри
жидкости, а также между жидкостью,
стенками сосуда и его дном, будут
отсутствовать.

Рис. 2-14. Цилиндрический сосуд, вращающийся
относительно вертикальной оси Oz
АОВ— свободная поверхность жидкости
Если оси координат,
расположенные, как показано на чертеже,
будем считать скрепленными с вращающимся
сосудом, то по отношению к таким
вращающимся осям координат жидкость
также будет находиться в покое. Поэтому
для исследования вращающейся жидкости
при указанных подвижных осях координат
могут быть применены известные уравнения
Эйлера (2-14).
В эти уравнения
входит объемная сила
,
действующая
на единицу массы жидкости. В данном
случае сила
будет слагаться
из двух сил: силы тяжести и центробежной
силы.
С тем чтобы найти
проекцию центробежной силы на оси
координат, наметим внутри жидкости
точку т
и выделим у
нее элементарную массу жидкости δM.
Масса δM
будет вращаться вокруг оси сосуда,
двигаясь по окружности, имеющей радиус
r
и лежащей в
плоскости, нормальной к оси сосуда.
Центробежная сила, действующая на данную
массу, будет
I’=,
(2-62)
где υ
– скорость
движения массы δM
по окружности
радиуса r.
Центробежная сила,
отнесенная к единице массы жидкости,
сосредоточенной в точке т,
I
=
= Ω2r. (2-63)
Эта сила, так же
как и сила I’,
направлена по радиусу от оси сосуда
наружу. Проекции силы I
(отнесенной к единице м- ассы) на оси
координат
Ix
= Ω2rcos(r,x)
= Ω2x
Iy
= Ω2rcos(r,y)
= Ω2y
Iz
= 0 (2-64)
Проекции объемной
силы тяжести, отнесенной к единице
массы, выражаются зависимостью (2-28).
Складывая объемные силы тяжести и
объемные центробежные силы, отнесенные
к единице массы, получаем
=
0 +Ω2x
= Ω2x;
=
0 + Ω2y
= Ω2y;
=
-(2-65)
Подставляя (2-65) в
(2-17), найдем
dpA
= ρ(Ω2xdx
+ Ω2ydy
–
,(2-66)
что после
интегрирования дает
dpA
= ρ(+–)
+ C =(x2
+
y2)
– ρC.
(2-67)
Постоянную
интегрирования С
устанавливаем, написав (2-67) применительно
к точке, находящейся в начале координат,
для которой x
= y
= z
=0; p
= p0.
Как видно,
C
= p0(2-68)
причем (2-67)
перепишется в виде:
pA
= p0
+
(x2
+y2)
– γz
(2-69)
Это последнее
уравнение и выражает закон распределения
давления в рассматриваемой жидкости.
Пользуясь таким уравнением, можно найти
поверхности равного давления.
Действительно,
уравнение поверхности, во всех точках
которой давление pA
= pi=
const,
запишется в виде
(x2
+y2)
– γz = pi
–
p0.
(2-70)
Уравнение (2-70)
выражает поверхность, являющуюся
параболоидом вращения (с вертикальной
осью).
Свободная поверхность
жидкости, характеризуемая постоянным
давлением pi
= p0,
представляет
собой также параболоид вращения;
уравнение ее будет:
(x2
+y2)
– γz
= 0.
(2-71)
Если учесть, что
x2
+ y2
= r2,
то, решив (2-71) относительно z,
получим следующее уравнение, по которому
легко построить параболу АОВ,
дающую свободную
поверхность:
z0
=
r2
(2-72)
где z0-
ордината кривой АОВ.
Распределение
давления в горизонтальной плоскости
MN,
лежащей ниже начала координат на величину
a,
можно найти,
пользуясь (2-69):
pA
= p0
+
(x2
+y2)
+γa = p0
+ ρr2+
γa = p0
+ γ(r2+
a). (2-73)
Учитывая (2-72),
получаем
pA
= p0
+ γ(a
+ z0)
= p0
+ γh
(2-74)
где h
= a
+z0
показано на рис. 2-14.
Таким образом,
давление в жидкости, находящейся внутри
равномерно вращающегося сосуда,
выражается зависимостью того же вида,
что и для случая тяжелой покоящейся
жидкости [см. (2-39)]; под величиной h
здесь надо
понимать только заглубление рассматриваемой
точки под криволинейной свободной
поверхностью.
Соседние файлы в папке Чугаев_1
- #
- #
- #
- #
- #
- #
Источник
Рассмотрим случай,
когда на жидкость, помимо объемных сил
тяжести, действует еще другая система
объемных сил, например, система
центробежных сил инерции.
Возьмем
круглоцилиндрический сосуд, наполненный
жидкостью, причем будем считать, что
этот сосуд вращается вокруг своей
вертикальной оси равномерно, т. е. с
постоянной угловой скоростью (рис.
2-14). Благодаря силам трения стенки
вращающегося сосуда будут вначале
увлекать за собой жидкость, а по истечении
некоторого времени вся жидкость начнет
вращаться вместе с сосудом с той же
угловой скоростью Ω,
находясь по отношению к стенкам сосуда
в покое. Силы трения при этом внутри
жидкости, а также между жидкостью,
стенками сосуда и его дном, будут
отсутствовать.

Рис. 2-14. Цилиндрический сосуд, вращающийся
относительно вертикальной оси Oz
АОВ— свободная поверхность жидкости
Если оси координат,
расположенные, как показано на чертеже,
будем считать скрепленными с вращающимся
сосудом, то по отношению к таким
вращающимся осям координат жидкость
также будет находиться в покое. Поэтому
для исследования вращающейся жидкости
при указанных подвижных осях координат
могут быть применены известные уравнения
Эйлера (2-14).
В эти уравнения
входит объемная сила
,
действующая
на единицу массы жидкости. В данном
случае сила
будет слагаться
из двух сил: силы тяжести и центробежной
силы.
С тем чтобы найти
проекцию центробежной силы на оси
координат, наметим внутри жидкости
точку т
и выделим у
нее элементарную массу жидкости δM.
Масса δM
будет вращаться вокруг оси сосуда,
двигаясь по окружности, имеющей радиус
r
и лежащей в
плоскости, нормальной к оси сосуда.
Центробежная сила, действующая на данную
массу, будет
I’=,
(2-62)
где υ
– скорость
движения массы δM
по окружности
радиуса r.
Центробежная сила,
отнесенная к единице массы жидкости,
сосредоточенной в точке т,
I
=
= Ω2r. (2-63)
Эта сила, так же
как и сила I’,
направлена по радиусу от оси сосуда
наружу. Проекции силы I
(отнесенной к единице м- ассы) на оси
координат
Ix
= Ω2rcos(r,x)
= Ω2x
Iy
= Ω2rcos(r,y)
= Ω2y
Iz
= 0 (2-64)
Проекции объемной
силы тяжести, отнесенной к единице
массы, выражаются зависимостью (2-28).
Складывая объемные силы тяжести и
объемные центробежные силы, отнесенные
к единице массы, получаем
=
0 +Ω2x
= Ω2x;
=
0 + Ω2y
= Ω2y;
=
-(2-65)
Подставляя (2-65) в
(2-17), найдем
dpA
= ρ(Ω2xdx
+ Ω2ydy
–
,(2-66)
что после
интегрирования дает
dpA
= ρ(+–)
+ C =(x2
+
y2)
– ρC.
(2-67)
Постоянную
интегрирования С
устанавливаем, написав (2-67) применительно
к точке, находящейся в начале координат,
для которой x
= y
= z
=0; p
= p0.
Как видно,
C
= p0(2-68)
причем (2-67)
перепишется в виде:
pA
= p0
+
(x2
+y2)
– γz
(2-69)
Это последнее
уравнение и выражает закон распределения
давления в рассматриваемой жидкости.
Пользуясь таким уравнением, можно найти
поверхности равного давления.
Действительно,
уравнение поверхности, во всех точках
которой давление pA
= pi=
const,
запишется в виде
(x2
+y2)
– γz = pi
–
p0.
(2-70)
Уравнение (2-70)
выражает поверхность, являющуюся
параболоидом вращения (с вертикальной
осью).
Свободная поверхность
жидкости, характеризуемая постоянным
давлением pi
= p0,
представляет
собой также параболоид вращения;
уравнение ее будет:
(x2
+y2)
– γz
= 0.
(2-71)
Если учесть, что
x2
+ y2
= r2,
то, решив (2-71) относительно z,
получим следующее уравнение, по которому
легко построить параболу АОВ,
дающую свободную
поверхность:
z0
=
r2
(2-72)
где z0-
ордината кривой АОВ.
Распределение
давления в горизонтальной плоскости
MN,
лежащей ниже начала координат на величину
a,
можно найти,
пользуясь (2-69):
pA
= p0
+
(x2
+y2)
+γa = p0
+ ρr2+
γa = p0
+ γ(r2+
a). (2-73)
Учитывая (2-72),
получаем
pA
= p0
+ γ(a
+ z0)
= p0
+ γh
(2-74)
где h
= a
+z0
показано на рис. 2-14.
Таким образом,
давление в жидкости, находящейся внутри
равномерно вращающегося сосуда,
выражается зависимостью того же вида,
что и для случая тяжелой покоящейся
жидкости [см. (2-39)]; под величиной h
здесь надо
понимать только заглубление рассматриваемой
точки под криволинейной свободной
поверхностью.
Соседние файлы в папке Чугаев
- #
- #
- #
- #
- #
- #
Источник
