Решение задач на сообщающиеся сосуды с разными жидкостями
План-конспект открытого урока по физике в 7А классе на тему «Сообщающиеся сосуды. Решение задач на сообщающие сосуды».
Цели урока:
Образовательные:
- Сформировать представление о сообщающихся сосудах и их свойствах;
- Показать примеры применение сообщающихся сосудов в быту и технике.
Развивающие:
- Развивать умения применять полученные знания на практике;
- Развивать экспериментальные умения, умения наблюдать, навыки логического мышления, умение обосновывать свои высказывания, делать выводы.
Воспитывающие:
- воспитывать интерес к познанию окружающего мира, любовь к родному краю;
- воспитывать коммуникативную культуру;
- создать условия для развития исследовательских навыков, навыков общения и совместной деятельности.
Тип урока: комбинированный.
Структура урока.
№ | Этапы урока | Время, мин | Приемы и методы |
1 | Организационный момент. | 3 | Рассказ учителя |
2 | Актуализация знаний. | 22 | Индивидуальные карточки, фронтальный опрос, индивидуальное задание, задание у доски. |
3 | Изучение нового материала. | 25 | Беседа. Записи на доске. Проведение эксперимента. Презентация на проекторе. Обсуждение результатов. Выводы. |
4 | Физическая пауза. | 3 | Делаем зарядку для глаз. Слушаем релаксирующую музыку. |
5 | Развитие знаний при решении задач. | 18 | Решение задач. |
6 | Подведение итогов. | 3 | Выделение главного учителем. Выставление оценок за работу на уроке. |
7 | Домашнее задание. | 1 | Запись на доске. |
Ход урока.
- Организационный момент.
(Поприветствовать класс, отметить отсутствующих, рассказать план урока)
План урока сегодня такой: проверяем д/з, изучаем новый учебный материал, учимся решать задачи по новой теме.
- Актуализация знаний.
Домой вам было задано повторить п.33-38. Проверим как вы выполнили Д/з.
- Выдать индивидуальные карточки на повторение материала (3-4 человека)
- Задание у доски (1-2 человека) – вывести формулу для расчета давления жидкости на дно и стенки сосуда.
- Провести фронтальный опрос по пройденному ранее материалу.
Остальные будут отвечать на мои вопросы:
– способы уменьшения давления (увеличивают площадь – шире колеса, гусеничный ход, фундамент зданий, широкие лямки рюкзака, лыжи, шпалы);
– способы увеличения давления (уменьшение площади – заточка инструментов, в природе – шипы, острый клюв, когти и зубы);
– чем вызвано давление газа (ударами молекул о станки сосуда);
– что происходит с газом при уменьшении объема (число ударов о стенки сосуда возрастет и давление увеличится);
– как зависит давление газа от температуры (увеличивается с увеличением температуры);
– почему сжатые газы содержат в специальных баллонах (т.к. при сжатии газа давление возрастает, что очень опасно, следовательно, баллоны должны быть очень прочные);
– сформулируйте Закон Паскаля (давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях);
– как показать на опыте, что давление внутри жидкости на разных уровнях разное (стеклянная колба с резиновой пленкой);
– почему во многих случаях не принимают во внимание давление газа, созданное его весом (из-за маленькой плотности газов);
– от каких величин зависит давление жидкости на дно сосуда (от плотности и от высоты столба жидкости);
– зависит ли давление жидкости на дно сосуда от формы сосуда, от площади поверхности (нет, нет).
- Проверяем правильность вывода формул у доски.
- Доклад учащегося на тему «Блез Паскаль. Биография и интересные факты жизни».
- Проверка карточек: 1 вариант (а, а, а, б, г, г)
2 вариант (в, б, г, в, в, а)
(Вопросы с ошибками предложить разобрать классу.)
- Изучение нового материала
А теперь приступим к НУМ.
Объявить тему урока. (Запись в тетрадях – число и тема урока)
- Сообщающие сосуды (определение, эксперименты)
Сегодня речь пойдет о сообщающихся сосудах. Как вы думаете, что это такое?
Записываем: «Сообщающимися сосудами называют сосуды, соединенные между собой в нижней части.»
Сообщающиеся сосуды мы встречаем в нашей жизни ежедневно. Попробуйте привести примеры (чайник, кофейник, лейка)
Научное открытие свойства сообщающихся сосудов датируется XI в (голландский ученый Стевин). Но оно было известно еще жрецам древней Греции. Археологи обнаружили в Грузии водопровод (XIII в), работающий по принципу сообщающихся сосудов.
С сообщающимися сосудами можно проделать простой опыт. Возьмем вот такие сообщающие сосуды (показываю). Наливаем воду и смотрим, что происходит (вода в обоих сосудах установилась на одном уровне). Возьмем теперь сообщающиеся сосуды разных форм и тоже нальем воду. Что вы заметили? (Вода тоже установилась во всех сосудах на одном уровне) Какой же вывод мы можем сделать?
Записываем: «Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне».
Докажем это с помощью формул:
Вывод формулы для случая с однородными жидкостями:
p1= ρgh1 p2= ρgh2
ρgh1= ρgh2
h1= h2
Ответим на вопросы: Изменится ли уровень жидкости, если правый сосуд будет шире левого? уже левого? если сосуды будут иметь разную форму? (Нет, жидкость установиться в обоих сосудах на одном уровне.) При изменении формы сосудов может изменяться лишь высота уровня воды в сосудах, отмеренная от уровня стола (из-за того, что изменяется объем сосудов). Однако уровни воды в сообщающихся сосудах не зависят от формы сосудов и останутся равны.
А как вы думаете, что произойдет, если в сообщающиеся сосуды налить две несмешивающиеся жидкости разной плотности?
Проверим это теоретически:
p1= ρ1gh1 p2= ρ2 gh2
ρ1gh1= ρ2gh2
ρ1h1= ρ2h2
Следовательно, высота столбов жидкостей в сосудах будет разной.
Записываем: При равенстве давлений высота столба жидкости большей плотности меньше, чем высота столба жидкости меньшей плотности.
- Применение сообщающихся сосудов в быту, природе, технике.
Где же применяются сообщающиеся сосуды?
Закон сообщающихся сосудов люди используют в разных технических устройствах: водопроводах с водонапорной башней; гидравлическом прессе; шлюзах; сифонах под раковиной, «водяных затворах» в системе канализации; действие артезианских колодцев и гейзеров основано на законе сообщающихся сосудов.
Еще один пример использования сообщающихся сосудов, это фонтаны. На них мы остановимся поподробнее.
В России существует единственный в мире комплекс фонтанов, который работает на принципе сообщающихся сосудов. Есть идеи, что это за фонтаны? Подсказка – эти фонтаны были созданы по распоряжению Петра 1. Это фонтаны в Петергофе. (Презентация1)
Рассмотрим для начала принцип действия фонтана (слайд2) Если уровень жидкости в обоих сосудах одинаковый, то фонтан бить не будет. Струя фонтана возникает под напором (давлением), который можно создать, если изменить уровень жидкости в одном из сосудов.
В современных фонтанах для создания давления на входе в трубы используются в большинстве случаев насосы (Слайд3). А в фонтанах Петергофа используется, как я уже говорила, принцип сообщающихся сосудов. Здесь нет ни насосов, ни сложных водонапорных сооружений. (Слайд4)
Петр не случайно выбрал именно это место для строительства загородной резиденции – Петергофа. (Слайд5) Обследуя местность вблизи Финского залива, он обнаружил множество водоемов и ключей, бьющихся из-под земли. По этим ключам можно было установить, что где-то неподалеку есть источник воды, расположенный выше уровня местности. Такой источник действительно был найден на Ропшинских высотах, расположенных на 100 м выше уровня моря.
Под руководством русского мастера Василия Туволкова в течение лета 1721 года были построены канал и другие водоводы, по ним из водоемов Ропшинских высот вода самотеком пошла в накопительные бассейны Верхнего сада Петродворца, объединив все озёра и ручьи. Здесь (в Верхнем саду) можно было уже устроить небольшие по высоте струи-фонтаны. А вот в Нижнем парке, на 16 метров ниже Верхнего сада, вода по трубам из накопительных бассейнов по принципу сообщающихся сосудов взмывает вверх множеством высоких струй в фонтанах парка. Далее она по прямому Морскому каналу, обрамленному множеством фонтанов, стекает в Финский залив.
У фонтанов есть свои секреты:
1. (Слайд6) Денег на возведение фонтанов в Петергофе потратили действительно немало, а вот энергии эти сооружения не расходуют совсем. Каждый фонтан в парке тратит 1000 литров в секунду, а в целом за день уходит до 8 млн литров воды. Однако, чтобы фонтан заработал, необходимо лишь с помощью вентиля открыть задвижку. При этом никакого постороннего звука от шумных моторов и механизмов вы не услышите, ведь их тут действительно нет.
2. (Слайд7) Под фонтанами находится огромное количество труб – маленьких и больших. Кстати, во времена Петра Великого не существовало прочных труб, их заменяли полые деревья, а чистить их приходилось изнутри очень худым детям. На ночь все фонтаны останавливают с помощью всё того же вентиля, а к утру всё вновь готово к полноценной работе. Зимой фонтаны не работают, а вода течёт задуманным ещё при Петре обходным путём через речку Шинкарка.
3. (Слайд8) Петергоф также известен своими фонтанами-шутками. По легенде, которую рассказывают экскурсоводы туристам, если наступить на один из камней, фонтан сразу же заработает. После рассказа все тут же спешат это проверить сами и тотчас попадают под брызги. Но никто из посетителей не замечает, что рядом с фонтаном сидит неприметный дяденька и держится за палку, которая со стороны похожа на трость. На самом деле именно он руководит процессом поступления воды. Рядом ещё с одним фонтаном находится будка с окошечком, в которой тоже сидит специальный человек. Такие невидимые сотрудники Петергофа несут свою вахту около каждого фонтана-шутки.
Многие уверены, что шикарные фонтаны дворцового комплекса работают на насосах. Однако из-за дороговизны такого процесса даже фонтаны во французском королевском дворце Версале включают только на 2 часа 2 раза в неделю. А в России, благодаря гениальной задумке Петра I и точному расчету русского инженера Туволкова, тысячи российских и иностранных туристов могут наслаждаться великолепием этих фонтанов ежедневно в течение всего лета.
На этом теоретическая часть нового материала закончена, приступим к практике, т.е. к решению задач.
- Развитие знаний при решении задач.
Физическая пауза. Прежде, чем приступить к решению задач, проведем “Гимнастику для глаз”.
- Зажмурьте глаза, а потом откройте их. Повторите 5 раз.
- Делайте круговые движения глазами: налево – вверх – направо – вниз – направо – вверх – налево – вниз. Повторите 10 раз.
- Закроем глаза, откинемся на спинку стула и послушаем музыку – 1 минуту. (Включить релаксирующую музыку)
Задача1: (Презентация2)
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16см?
Дано:
hрт = 16см = 0,16м
ρрт = 13600 кг/м3
ρн = 800 кг/м3
Найти:
hн – ?
Решение:
Запишем формулу для давления:
Р = ρgh
По условию задачи Ррт = Рн, или ρрт ghрт = ρнghн, отсюда
hн = (ρртhрт) / ρн
hн = 2,7м
Ответ: hн = 2,7м
Задача2: №26.22 (Задачник, стр. 130) Прочитаем условие задачи. Предложить учащимся выйти у доске и решить задачу.
Решение: Уровни ртути будут совпадать, если давление столба воды и столба керосина одинаково: pв = pк, т.к. давление определяется по формуле:
p = ρ · g · h ,
то ρв · g · h в = ρк · g · h к. Отсюда находим h к = ρв · g · h в/ ρк · g, производя математическое действие, получим: h к = ρв· h в/ ρк :
h к = ρв· h в/ ρк = 1000 кг/м3 ·0,2м /800 кг/м3 = 0,25м=25см
Ответ: 25см
Задача2: 26.7
В сосуде с керосином уровень будет больше, т.к. плотность керосина меньше плотности воды.
Задача3: №26.23 (Задачник) ?
- Итоги урока.
Сегодня мы с вами изучили сообщающиеся сосуды. Что вы запомнили из урока? Что такое сообщающиеся сосуда? Какой будет уровень в сообщающихся сосудах при однородных жидкостях? При неоднородных жидкостях? Где используется принцип сообщающихся сосудов?
Выставляются оценки за работу на уроке, оценки озвучиваются.
- Домашнее задание.
Запишите пожалуйста домашнее задание. На доске: п. 39, зад. 26.2, 26.13 (задачник)
Урок закончен. До свидания!
Источник
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
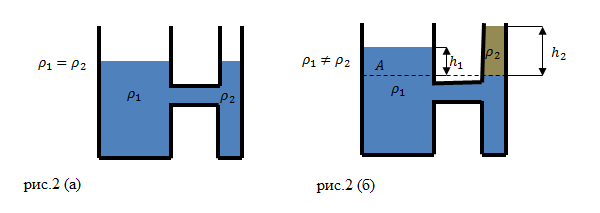
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
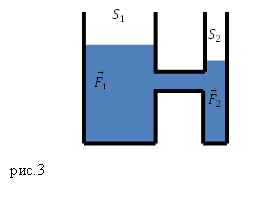
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.

Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
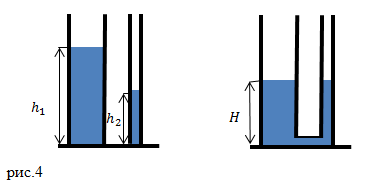
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник
