Решение задач по физике в сосуд с водой

В последнее время мы разбирали решения многих простейших физических задач по разным темам: законы Ньютона, сила трения, свободное падение и т.д. Пришла пора взяться за что-то посложнее. Сегодня решаем задачи по теме «гидростатика».
За полезными лайфхаками и новостями студенческой жизни добро пожаловать на наш телеграм-канал.
Задачи по гидростатике с решениями
Задача №1 на гидростатику
Условие
B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает?
Решение
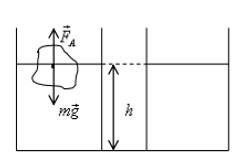
По условию плавания тел:
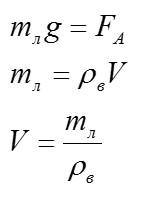
V – объем погруженной в воду части льда. После таяния льда образуется объем воды:
Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.
Ответ: уровень не изменится.
Задача №2 на гидростатику
Условие
Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?
Решение
Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:
Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:
В одном кубическом метре – тысяча литров.
Ответ: 2 литра.
Задача №3 на гидростатику
Условие
Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.
Решение
Вспоминаем основное уравнение гидростатики и записываем:
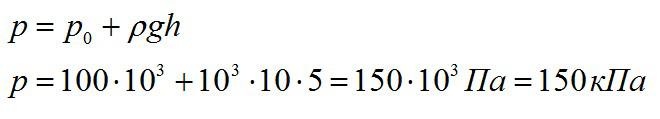
Ответ: 150 кПа.
Задача №4 на гидростатику
Условие
Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.
Решение
Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.
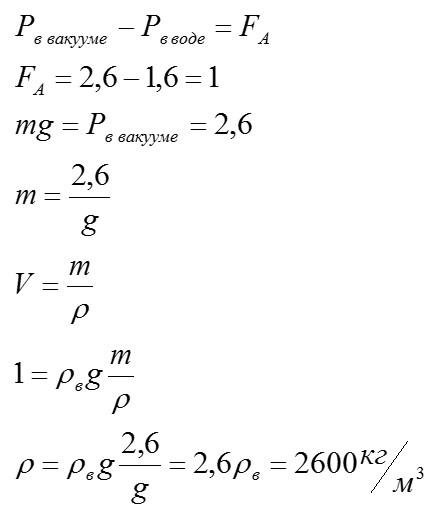
Ответ: 2600 кг/м3.
Задача №5 на гидростатику
Условие
Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?
Решение
Формула для гидростатического давления:
Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.
Ответ: высота увеличилась в 5 раз.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы по гидростатике
Вопрос 1. Что такое гидростатический парадокс?
Ответ. Гидростатический парадокс – явление, когда вес жидкости в сосуде не совпадает с весовым давлением, которое она оказывает на стенки сосуда. Возникает в сосудах конусообразной формы.
Вопрос 2. Какие есть внесистемные единицы изменения давления:
Ответ. Внесистемные единицы давления:
- миллиметр ртутного столба;
- бар;
- атмосфера.
Вопрос 3. В условиях физических задач часто можно встретить формулировку «нормальные условия». Что этот значить?
Ответ. Это значит, что давление нужно брать равным 101325 Па (или 760 мм рт. ст.), а температуру – 0 градусов Цельсия (или 273 Кельвина).
Вопрос 4. Что такое сообщающиеся сосуды?
Ответ. Сообщающиеся сосуды – это емкости, соединенные между собой. Жидкость может свободно перетекать из одного сосуда в другой. Уровень жидкости с одной плотностью в сообщающихся сосудах всегда одинаков. Простейший пример сообщающихся сосудов: обычный чайник. Если мы нальем в него воду, уровень будет одинаковым как в носике, так и в основном объеме. Если же плотности жидкостей разные, то выше будет уровень той, у которой плотность меньше.
Вопрос 5. Что такое гидравлический пресс?
Ответ. Гидравлический пресс – устройство, в основе действия которого лежит закон Паскаля и принцип сообщающихся сосудов. Пресс состоит из двух соединённых и заполненных маслом цилиндров: узкого и широкого. При нажатии на поршень узкого цилиндра, широкий цилиндр получает во столько раз большее давление, во сколько раз площадь большего поршня больше площади меньшего поршня.
Гидростатика: немного теории
Гидростатика – раздел физики, изучающий равновесие жидкостей.
Равновесие жидкостей – очень важный раздел. Например, если вы выпили много пива, просто необходимо, чтобы оно находилось в равновесии. Но шутки в сторону! Какие фундаментальные понятия нужно знать, чтобы решать задачи по гидростатике?
Давление и плотность
Давление – физическая величина, равная отношению модуля силы, перпендикулярно действующей на поверхность, к площади этой поверхности.
Давление столба жидкости называют гидростатическим, а измеряется оно в Паскалях. Гидростатическое давление столба жидкости высотой h на дно сосуда рассчитывается по формуле:
Греческое «ро» – плотность жидкости. Плотность измеряется в килограммах на кубический метр и равна отношению массы тела к его объему.
Жидкость – изотропная среда. Это значит, что ее свойства одинаковы в любой ее точке.
Закон Паскаля и основное уравнение гидростатики
Давление, оказываемое на жидкость или газ передается в любую точку этой жидкости одинаково и во всех направлениях.
Это и есть закон Паскаля. Согласно ему, давление жидкости зависит только от плотности жидкости и высоты ее столба. На глубине h жидкость оказывает одинаковое давление как на дно, так и на стенки сосуда.
В данном случае р нулевое – давление столба воздуха (атмосферы), которое действует на жидкость.
В своей другой формулировке основное уравнение гидростатики показывает, что гидростатический напор является постоянной величиной для всего объема неподвижной жидкости. Здесь мы не будем останавливаться на этом понятии, так как оно изучается в курсе гидравлики.
Закон Архимеда и условия плавания тел
Закон Архимеда – еще одна важнейшая часть гидростатики. Он гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Тело плавает, если выталкивающая сила Архимеда больше действующей на него силы тяжести. Это же условие можно переписать, используя понятие плотности: тело будет плавать, если плотность жидкости больше, чем плотность тела.
Подробнее о законе Архимеда и фактах из жизни этого выдающегося античного инженера читайте в нашем отдельном материале.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис за качественным и быстрым объяснением.
Источник
Условие задачи:
В сосуд с водой объемом 0,25 л при 20 °C поместили 50 г расплавленного свинца с температурой 400 °C. Какая температура установится в результате теплообмена в сосуде? Удельные теплоёмкости расплава и твердого свинца считать одинаковыми.
Задача №5.2.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(V_1=0,25) л, (t_1=20^circ) C, (m_2=50) г, (t_2=400^circ) C, (t-?)
Решение задачи:
В этой задаче нужно обязательно произвести оценку. Давайте для начала определим количество теплоты (Q_1), которое необходимо для нагревания воды массой (m_1) от температуры (t_1) до температуры кипения (t_к) ((t_к=100^circ) C). Это можно сделать по следующей формуле:
[{Q_1} = {c_1}{m_1}left( {{t_к} – {t_1}} right)]
Удельная теплоёмкость воды (c_1) равна 4200 Дж/(кг·°C).
Массу (m_1) представим как произведение плотности воды (rho) (она равна 1000 кг/м3) на объем (V_1), тогда:
[{Q_1} = {c_1}rho {V_1}left( {{t_к} – {t_1}} right)]
Посчитаем численное значение (Q_1) (объем при расчете мы перевели в кубические метры):
[{Q_1} = 4200 cdot 1000 cdot 0,25 cdot {10^{ – 3}} cdot left( {100 – 20} right) = 84000;Дж]
Так как температура расплавленного свинца (t_2) больше температуры его плавления (t_п) ((t_п=327^circ) C), то определим количество теплоты (Q_2), выделяемое при охлаждении расплава свинца от температуры (t_2) до температуры (t_п).
[{Q_2} = {c_2}{m_2}left( {{t_2} – {t_п}} right)]
Удельная теплоёмкость расплава свинца (и твёрдого свинца) (c_2) равна 130 Дж/(кг·°C).
[{Q_2} = 130 cdot 0,05 cdot left( {400 – 327} right) = 474,5;Дж]
Количество теплоты (Q_3), выделяемое при кристаллизации свинца массой (m_2), определим по формуле:
[{Q_3} = lambda {m_2}]
Удельная теплота кристаллизации (плавления) свинца (lambda) равна 25 кДж/кг.
[{Q_3} = 25 cdot {10^3} cdot 0,05 = 1250;Дж]
Количество теплоты (Q_4), выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t_к), равно:
[{Q_4} = {c_2}{m_2}left( {{t_п} – {t_к}} right)]
[{Q_4} = 130 cdot 0,05 cdot left( {327 – 100} right) = 1475,5;Дж]
Видно, что ({Q_1} > {Q_2} + {Q_3} + {Q_4}), значит температура теплового равновесия будет лежать в пределах от (t_1) до (t_к). Запишем уравнение теплового баланса:
[{Q_5} = {Q_2} + {Q_3} + {Q_6}]
Здесь (Q_5) – количество теплоты, необходимое для нагревания воды массой (m_1) от температуры (t_1) до температуры (t); (Q_6) – количество теплоты, выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t). Тогда:
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – {t_п}} right) + lambda {m_2} + {c_2}{m_2}left( {{t_п} – t} right)]
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – t} right) + lambda {m_2}]
Раскроем скобки:
[{c_1}{m_1}t – {c_1}{m_1}{t_1} = {c_2}{m_2}{t_2} – {c_2}{m_2}t + lambda {m_2}]
Все члены с множителем (t) перенесем в левую сторону, вынесем его за скобки, остальные перенесем в правую.
[tleft( {{c_1}{m_1} + {c_2}{m_2}} right) = {c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}]
[t = frac{{{c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}{m_1} + {c_2}{m_2}}}]
Массу (m_1) представим как произведение плотности воды (rho) на объем (V_1), как это уже было сделано выше:
[t = frac{{{c_1}rho {V_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}rho {V_1} + {c_2}{m_2}}}]
Переведём некоторые величины в систему СИ:
[0,25;л = 0,25 cdot {10^{ – 3}};м^3]
[50;г = 0,05;кг]
Численно температура (t) равна:
[t = frac{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} cdot 20 + 130 cdot 0,05 cdot 400 + 25 cdot {{10}^3} cdot 0,05}}{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} + 130 cdot 0,05}} = 23,5^circ;C = 296,5;К]
Ответ: 296,5 К.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
Модуль 17 Вариант 1 | Решение задач по теме «Закон Архимеда. Условия плавания тел» | |
Цель модуля. УМЕТЬ решать простейшие и комбинированные задачи по теме «Закон Архимеда. Условия плавания тел» |
Учебный материал
Свои способности человек может
узнать, только попытавшись применить их на деле.
Сенека
Проверка домашнего задания. Упражнение 22. Цель: ПРОВЕРИТЬ правильность выполнения домашнего задания. | ||||||||||||||||||
1. Однородные шары одинакового объема из парафина, пробки, оргстекла и алюминия опускают в воду. Изобразите положения шаров в воде. У каких из не потонувших шаров глубина погружения в воде больше? Решение: Определим плотности шаров. , , , Ответ: глубина погружения больше у парафина. 2. Массы кирпича и железного бруска одинаковы. Какое из этих тел легче держать в воздухе? В воде? Решение: В воздухе, если не учитывать выталкивающую силу воздуха, вес тел одинаковый. Значит, их держать одинаково легко. В воде вес тела становится меньше на значение равное выталкивающей силе, которая равна , ,, , . Значит, объем кирпича больше, чем объем железного бруска. Отсюда можем сделать вывод, что выталкивающая сила, действующая на кирпич, больше. Значит, кирпич легче держать в воде. Ответ: кирпич легче держать в воде. 3. Определите силу Архимеда, действующую на мальчика, нырнувшего в воду. Объем тела мальчика V=0,03 м3. Коэффициент g=10 Н/кг.
4. На гайку, погруженную в керосин, действует выталкивающая сила F= 16 мН. Определите объем гайки.
5. На сколько легче поднимать в воде. Чем в воздухе гранитную плиту объемом V=12. (Архимедовой силой, создаваемой воздухом можно пренебречь.)
6. Динамометр с висящим телом в воздухе показывает F1=2 Н, а в воде при полном погружении тела – F2=1,6 Н. Определите объем тела и плотность вещества.
7. На наполненный гелием шар объемом V=6 дм3 действует в воздухе выталкивающая сила F= 72 мН. Определите плотность воздуха.
8. Пенопластовый буй объемом V=4 дм3 удерживается леской так, что ровно половина его погружена в воду. Какие силы действуют на буй? Определите значение каждой из них. Плотность пенопласта ρпенопл.=200 кг/м3.
9. Сосуд с водой установлен на столике динамометра, который показывает силу F=6 Н. Какими станут показания динамометра, если алюминиевый груз объемом V=14 см3 опустить в воду сначала так, чтобы он не касался дна, а затем так, чтобы он лёг на дно сосуда при опущенной нитке?
10. Определите плотность вещества тела, частично погруженного в воду, если под водой находится одна треть его объема.
11. При полном погружении в воду алюминиевой детали массой m=405 г с воздушной полостью внутри действует выталкивающая сила F=2 H. Определите объем полости.
|
Самостоятельная работа. Решение несложных качественных и расчетных задач.
Цель: УМЕТЬ применять формулу для вычисления архимедовой силы и производные от неё. ЗНАТЬ условия плавания тел.
1. К одинаковым пружинам подвешены тела из меди, стали, цинка равной массы. Пружина с каким телом сократится больше, если тела полностью погрузить в воду?
а.  Пружина с телом из меди.
Пружина с телом из меди.
б. Пружина с телом из цинка.
в. Пружина с телом из стали.
г. Все пружины сократятся одинаково.
2. Сравните выталкивающие силы, действующие на шары одинаковой массы, погруженные в жидкость.
а. На все шары действуют одинаковые выталкивающие силы.
б. Большая сила действует на шар А.
в. Большая сила действует на шар Б.
г. Большая сил а действует на шар В.
Стальная деталь массой 4,68 кг погружена в машинное масло.
3. Каков объем вытесненной жидкости?
а. 600 см3. б. 60 см3. в. 6 см3. г. 0,6 см3.
4. Вычислите архимедову силу, действующую на эту деталь.
а. 5,4 Н. б. 0,54 Н. в. 6 Н. г. 4,68 Н.
5. Какую силу нужно приложить, чтобы поднять ее в жидкости?
а. 4,68 Н.
б. 46,8 Н.
в. 41,4 Н.
г. 36,8 Н.
Решение задач
Цель: РЕШАТЬ задачи на вычисление архимедовой силы, а так же задачи с применением знаний о условиях плавания тел.
Задача 1. Однородные шары одинакового объема из полиэтилена, сухого дуба, сухой сосны и бетона опускают в воду. Изобразите положения шаров в воде. У каких из не потонувших шаров глубина погружения в воде больше?
Задача 2. Массы кирпича и куска льда одинаковы. Какое из этих тел легче держать в воздухе? В воде?
Задача 3. Определите силу Архимеда, действующую на человека, нырнувшего в воду. Объем тела человека V=0,06 м3. Коэффициент g=10 Н/кг.
Задача 4. На болт, погруженный в машинное масло, действует выталкивающая сила F= 18 мН. Определите объем болта.
Задача 5. На сколько легче поднимать в воде, чем в воздухе железную плиту объемом V=20. (Архимедовой силой, создаваемой воздухом можно пренебречь.)
Задача 6. Вычислите выталкивающую силу, действующую на гранитную глыбу, которая при полном погружении в воду вытесняет её некоторую часть. Объем вытесненной воды равен 0,8 м3.
Задача 7*. Стальной брусок, вес которого 15,6 Н, погрузили в воду. Определите значение и направление силы натяжения пружины.
Выходной контроль
Цель: ПРОВЕРИТЬ усвоение учебных элементов.
1. На рисунке показаны одинаковые тела, находящиеся в сосудах с разными жидкостями. В каком сосуде плотность жидкости наибольшая?
а) А; в) В;
б) Б; г) Г.
2. В воду погружены бруски одинакового объема. У кого из них меньше плотность?
а) У всех брусков одинаковая плотность;
б) А; в)Б; г)В.
3. Не меньше какой длины нужно иметь верёвку, чтобы с плавающей льдины толщиной 2 м зачерпнуть ведро воды?
а) 0,2 м; б) 2 м; в) 1 м; г) 0,5 м.
Подведение итогов
Цель: ЗАПОЛНИТЬ лист контроля; ОЦЕНИТЬ знания.
ЛИСТ КОНТРОЛЯ
Учебный элемент | Ответ | Баллы | Результат |
Самостоятельная работа | 1. б 2. г 3. а 4. а 5. в | 2 2 3 3 3 | Поставьте себе итоговую оценку: 35-46 баллов – «отлично»; 23-34 баллов – «хорошо»; 11 -22 баллов – «зачет»; ≤ 10 баллов – «незачет». Сдайте лист контроля учителю. ОЦЕНКА ↓ |
Решение задач | 1. Наибольшая глубина погружения у шара из полиэтилена 2. В воздухе кирпич и лед имеют одинаковый вес. В воде легче держать лед. 3. 600 Н 4. 2 см3 5. 0,2 кН 6. 8 кН 7. 13,6 Н. Направлена вертикально вверх. | 2 2 3 4 4 4 8 | |
Выходной контроль | 1. б 2. в 3. а | 2 2 2 | |
Итого: | 46 |
ДОМАШНЕЕ ЗАДАНИЕ: повторить §§36-37, задачи:
«незачет» | «зачет» | «хорошо» | «отлично» |
№ 1-2 | № 3 | № 4, 5 | № 6, 7 |
1. Однородные шары одинакового объема из полиэтилена, сухой сосны, фарфора, мрамора и цинка опускают в воду. Изобразите положения шаров в воде. У каких из не потонувших шаров глубина погружения в воде больше?
2. Массы кирпича и сухого дуба одинаковы. Какое из этих тел легче держать в воздухе? В воде?
3. Определите силу Архимеда, действующую на человека, нырнувшего в воду. Объем тела человека V=0,08 м3. Коэффициент g=10 Н/кг.
4. На болт, погруженный в серную кислоту, действует выталкивающая сила F= 18 мН. Определите объем болта.
5. На сколько легче поднимать в воде, чем в воздухе плиту из олова объемом V=20. (Архимедовой силой, создаваемой воздухом можно пренебречь.)
6. Железобетонная плита размером 3,5×1,5×0,2 м полностью погружена в воду. Вычислите архимедову силу, действующую на плиту.
7*. Известно, что масса мраморной плиты равна 40,5 кг. Какую силу надо приложить, чтобы удержать эту плиту в воде?
Воспитанные люди уважают человеческую личность,
а потому всегда снисходительны, мягки, вежливы, уступчивы.
Антон Павлович Чехов
Рефлексия. Дайте эмоциональную оценку своей деятельности на уроке.
Источник
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела – и котёл, и вода – будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С – 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2. Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3. Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4. В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5. На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6. По графику определите удельную теплоёмкость образца, если его масса 50 г.
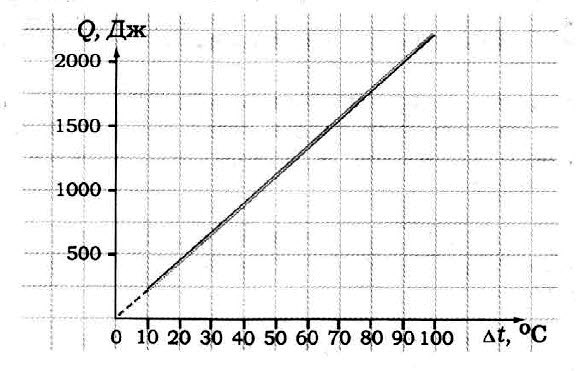

Задача № 7. Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8. Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
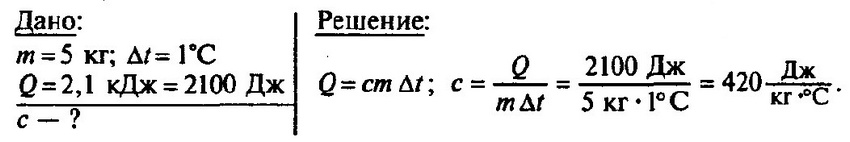
Задача № 9. Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10. Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11. а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12. ОГЭ Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13. В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Задача № 14. (повышенной сложности) Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
