Решение задач с теплоизолированным сосудом

Эти задачи я использовала при подготовке к олимпиаде семи- и восьмиклассников. Также можно решать их для подготовки к ЕГЭ, для более глубокого проникновения в тему.
Задача 1. На дне глубокой шахты лежало 700 кг льда при температуре С. В шахту сбросили 678 л горячей воды. В момент падения на лед ее температура равнялась С, весь лед при этом растаял. На какой наименьшей глубине находился в шахте лед, если удельная теплоемкость воды равна 4,2 кДж/(кгС), а удельная теплота плавления льда равна кДж/кг? Трением о воздух в процессе падения пренебречь.
Определим, сколько нужно джоулей, чтобы растопить весь лед:
Теперь посмотрим, сколько джоулей отдаст вода, если остынет на С, то есть до нулевой температуры:
Здесь подставлена масса воды, думаю, всем понятно, что 678 л воды имеют массу 678 кг?
То есть тепла, связанного с остыванием воды, нам не хватит, чтобы растопить весь лед. Поэтому надо подумать, откуда взялась разница между и . Вода, падая, набрала скорость, то есть обладала кинетической энергией. Эта энергия и преобразовалась в тепло. А превратилась эта энергия в кинетическую из потенциальной, которой вода обладала вверху. Тогда
Ответ: м – минимальная высота падения.
Задача 2. Сосуд наполнен до краев водой массой кг с температурой С. В него аккуратно опускают кусок льда массой кг, имеющий температуру С. Какая температура установится в сосуде? Удельная теплоемкость воды c = 4200 Дж/(кгC), удельная теплота плавления льда кДж/кг. Тепловыми потерями пренебречь.
Так как сосуд наполнен до самых краев, то часть воды выльется. Определим, какая это будет часть. Масса вылившейся воды совпадает с массой льда. В этом можно убедиться через давление на дно: если лед уже плавает в сосуде, то, растаяв, он тем самым давление на дно не изменит, а значит, объем вылившейся воды совпадает с объемом погруженной части льда или, попросту, равны массы льда и вылившейся воды.
Таким образом, вылилось 2,1 л воды. Зная плотность воды, находим, что масса этого объема воды 2,1 кг. Тогда воды в сосуде осталось
Составим уравнение теплового баланса: потребителями тепла будут лед (на таяние) и получившаяся изо льда вода (на согрев). Отдаст это тепло та вода, что была в сосуде ().
Ответ: .
Задача 3. В бассейн по трубе, в которой установлен нагреватель мощностью МВт, подается вода из резервуара. Температура воды в резервуаре С. В первый раз пустой бассейн заполняется за время мин, при этом температура воды после заполнения С. Во второй раз в бассейне было изначально некоторое количество воды при температуре С. Оставшуюся часть заполняли также время мин. Температура воды после заполнения оказалась C. Сколько воды первоначально было в бассейне во втором случае? Остыванием воды в бассейне пренебречь. Теплоемкость воды Дж/кгС.
Мощность нагревателя постоянна, следовательно, он от дал в обоих случаях одно и то же количество теплоты, так как работал одно и то же время. В первом случае тепло пошло на нагрев полного бассейна (вода нагрелась с 5 до 20 градусов, то есть на 15):
Откуда можно узнать, сколько всего воды по массе помещается в бассейне.
Итак, в бассейне 20 тонн воды. Пусть часть воды, которая была в бассейне во второй раз, равна , а часть, которую мы грели, . Следовательно,
Теперь составляем уравнение баланса. Воду массой мы нагрели на 10 градусов, а часть – на 20.
Так как
То
Ответ: 10000 кг, или 10 т
Задача 4. На плите стоит кастрюля с водой. При нагревании температура воды увеличилась от C до C за одну минуту. Какая доля теплоты, получаемой водой при нагревании, рассеивается в окружающем пространстве, если время остывания той же воды от C до C равно 9,0 минутам?
Так как вода нагрелась в первом случае на 5 градусов, и потом остыла на те же пять градусов, то приобретенное и потерянное количество теплоты – одно и то же. Сначала вода получала тепло от плиты, но и теряла его тоже:
Потом – только теряла тепло:
Тогда
Ответ: 0,1
Задача 5. В теплоизолированном сосуде находится смесь льда массой кг и воды. После начала нагревания температура смеси оставалась постоянной в течение времени мин, а затем за время мин повысилась на С. Определите массу смеси, если считать, что количество теплоты, получаемое системой в единицу времени, постоянно. Удельная теплота плавления льда кДж/кг, а удельная теплоемкость воды кДж/(кгК). Теплоемкостью сосуда пренебречь.
Сначала шло таяние льда, так как температура не менялась. Тогда можно записать, что на плавление льда пошло тепло, равное:
Потом нагревалась вода, которая была в сосуде и вода, получившаяся изо льда:
Так как – постоянно, то
Ответ: 3 кг
Задача 6. Кусок льда с вмерзшими в него свинцовыми дробинками общей массой 200 г осторожно опускают в стакан калориметра, доверху наполненный водой. Часть воды при этом выливается и в дальнейшем теплообмене не участвует. Когда система пришла в состояние теплового равновесия, оказалось, что температура воды в калориметре С . Начальные температуры воды С, льда С. Масса воды в калориметре была 1,2 кг. Определите объемное содержание свинца в куске льда. Теплоемкостью калориметра пренебречь.
Предположим, что лед со свинцом будет плавать, а не тонуть. Тогда по закону Архимеда он вытеснит такой объем воды, что вес этого объема 200 г. То есть воды останется литр. Запишем уравнение теплового баланса для этой системы.
Зная, что
Выразим массу льда (или свинца)
И подставим в уравнение теплового баланса:
Упрощая это выражение и подставляя все константы, получим
Тогда
Объемное содержание свинца равно
Ответ: .
Задача 7. Волшебник готовит в аптекарском стакане емкостью 0,3 л целебную смесь. Он налил в стакан доверху живую воду температурой С. К сожалению, стакан с водой остывает на С за пять минут. Для того, чтобы смесь не остывала, волшебник капает в стакан обыкновенную теплую воду с температурой С. Масса одной капли 0,2 г. Сколько капель в минуту нужно капать в стакан, чтобы температура в нем поддерживалась равной С? На сколько нагреется за одну минуту вода в стакане, если капать в три раза чаще? Теплоемкости живой и обычной воды совпадают. Лишняя вода выливается из носика.
Будем считать, что как только капля обычной воды попадает в стакан, из его носика сразу же падает капля живой, и более в теплообмене не участвует.
Давайте определим, какое количество теплоты теряет стакан за пять минут. Масса воды в нем нам известна, следовательно,
Следовательно, простая вода должна «принести» 1260 Дж, чтобы стакан не остывал. При этом простая вода охлаждается на градусов. Тогда
Приравнивая количества теплоты, имеем:
Разделим эту массу на массу капли, чтобы узнать их количество:
Так как капать надо в течение 5 минут, то получается, по 15 капель в минуту.
Если капать в три раза чаще, то число капель в минуту будет равняться 45, причем первые 15 капель в минуту будут приносить энергию, достаточную, чтобы поддерживать уровень температуры, а еще 30 капель уже будут нагревать воду в стакане. Следовательно, на нагрев пойдет Дж. Это количество тепла нагреет стакан массой 0,3 кг на
На 2 градуса за 5 минут, следовательно, на 0,4 градуса за минуту.
Ответ: а) 15 капель в минуту; б) на 0,4 градуса.
Задача 8. Теплоизолированный сосуд был до краев наполнен водой при температуре С. В середину этого сосуда быстро, но аккуратно опустили деталь, изготовленную из металла плотностью кг/м, нагретую до температуры С, и закрыли крышкой. После установления теплового равновесия температура воды в сосуде стала равна С. Затем в этот же сосуд, наполненный до краев водой при температуре С, вновь быстро, но аккуратно опустили две такие же детали, нагретые до той же температуры С, и закрыли крышкой. В этом случае после установления в сосуде теплового равновесия температура воды равна С. Чему равна удельная теплоемкость металла, из которого изготовлены детали? Плотность воды 1000 кг/м. Удельная теплоемкость воды Дж/(кг *К).
Запишем уравнение теплового баланса для обоих случаев. В первом случае из сосуда выльется объем воды, равный .
Во втором случае из сосуда выльется вода в количестве :
Выразим в обоих случаях и приравняем, таким образом мы исключим эту величину. Из первого уравнения:
Из второго уравнения:
Тогда
Объем детали сократится.
Подставим числа:
Подсчеты дают Дж/(кг*К)
Ответ: Дж/(кг*К).
Источник
1. Поскольку в указанном процессе газ не совершает работы и система является теплоизолированной, то в соответствии с первым законом термодинамики суммарная внутренняя энергия газов сохраняется:
где – температура в объединённом сосуде в равновесном состоянии после открытия крана.
2. В соответствии с уравнением Клапейрона – Менделеева для конечного состояния можно записать:
Исключая из двух записанных уравнений конечную температуру получаем искомое выражение для начальной температуры аргона:
K.
Ответ: K
Порядок назначения третьего эксперта
В соответствии с Порядком проведения государственной итоговой аттестации по образовательным программам среднего общего образования (приказ Минобрнауки России от зарегистрирован Минюстом России )
« По результатам первой и второй проверок эксперты независимо друг от друга выставляют баллы за каждый ответ на задания экзаменационной работы ЕГЭ с развёрнутым ответом…
В случае существенного расхождения в баллах, выставленных двумя экспертами, назначается третья проверка. Существенное расхождение в баллах определено в критериях оценивания по соответствующему учебному предмету.
Эксперту, осуществляющему третью проверку, предоставляется информация о баллах, выставленных экспертами, ранее проверявшими экзаменационную работу».
Если расхождение составляет и более балла за выполнение задания, то третий эксперт проверяет ответ на задание.
Критерии оценки
3 баллаПриведено полное решение, включающее следующие элементы:
I. записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: формула для заряда
конденсатора, закон сохранения заряда, выражение для энергии
конденсатора, ёмкости параллельно соединённых конденсаторов,
закон сохранения энергии);
II. описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов);
III. проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
IV. представлен правильный ответ с указанием единиц измерения
искомой величины
2 баллаПравильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения (не
зачёркнуты; не заключены в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в
записи единиц измерения величины)
1 баллПредставлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
данной задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения данной задачи (или утверждение, лежащее в основе
решения), но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной
задачи (или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи
0 балловВсе случаи решения, которые не соответствуют вышеуказанным
критериям выставления оценок в балла
Источник
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
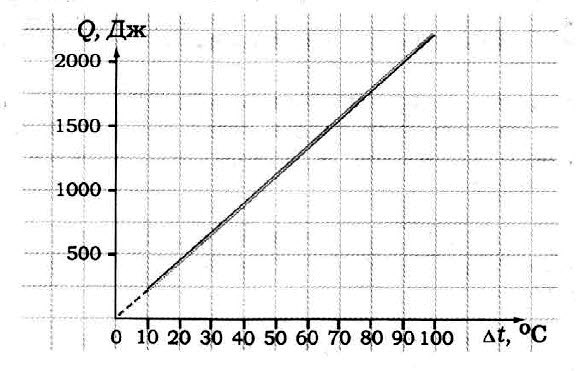

Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
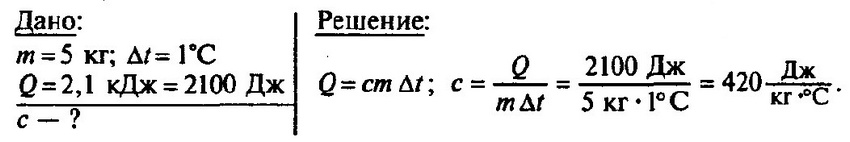
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Задача № 14. (повышенной сложности)
Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
Задачи из ДЕМОВАРИАНТОВ (с решениями)
1. Воздушный шар, оболочка
которого имеет массу М = 145 кг и объем V =
230 м3, наполняется горячим воздухом при нормальном
атмосферном давлении и температуре окружающего воздуха tо
= 0оС. Какую минимальную температуру t должен
иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка
шара нерастяжима и имеет в нижней части небольшое отверстие.
Образец возможного решения
2. Воздушный
шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием.
Он может удерживать в воздухе на высоте, где температура воздуха
17оС, а давление 105 Па, груз массой 225
кг. Какова масса гелия в оболочке шара? Считать, что оболочка
шара не оказывает сопротивления изменению объема шара.
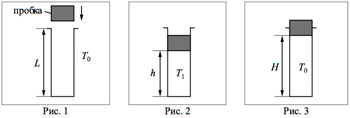
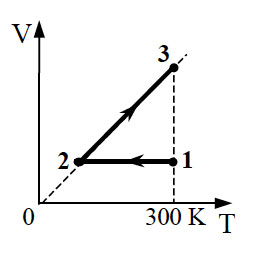
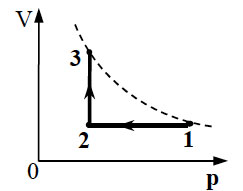
Образец возможного решения2*. В камере, заполненной азотом, при температуре T = 300 К находится открытый цилиндрический сосуд (см. рис. 1). Высота сосуда L = 50 см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до температуры T1. В результате расстояние от дна сосуда до низа пробки становится равным h = 40 см (см. рис. 2). Затем сосуд нагревают до первоначальной температуры T0. Расстояние от дна сосуда до низа пробки при этой температуре становится равным H = 46 см (см. рис. 3). Чему равна температура T1? Величину силы трения между пробкой и стенками сосуда считать одинаковой при движении пробки вниз и вверх. Массой пробки пренебречь. Давление азота в камере во время эксперимента поддерживается постоянным.
Образец возможного решения
3. В медный
стакан калориметра массой 200 г, содержащий 150 г воды, опустили
кусок льда, имевший температуру 0°С. Начальная температура калориметра
с водой 25°С. В момент времени, когда наступит тепловое равновесие,
температура воды и калориметра стала равной 5°С. Рассчитайте массу
льда. Удельная теплоемкость меди 390 Дж/кг•К, удельная теплоемкость
воды 4200 Дж/кг•К, удельная теплота плавления льда 3,35•105
Дж/кг. Потери тепла калориметром считать пренебрежимо малыми.
Образец возможного решения4. Необходимо расплавить лёд массой 0,2 кг,
имеющий температуру 0оС. Выполнима ли эта задача,
если потребляемая мощность нагревательного элемента – 400 Вт,
тепловые потери составляют 30%, а время работы нагревателя не
должно превышать 5 минут?
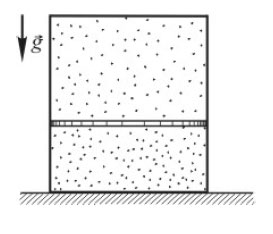
Образец возможного решения4*. Теплоизолированный горизонтальный сосуд разделён пористой перегородкой на две равные части. В начальный момент в левой части сосуда находится ν = 2 моль гелия, а в правой – такое же количество моль аргона. Атомы гелия могут проникать через перегородку, а для атомов аргона перегородка непроницаема. Температура гелия равна температуре аргона: Т = 300 К. Определите отношение внутренних энергий газов по разные стороны перегородки после установления термодинамического равновесия.
Образец возможного решения4**. Теплоизолированный цилиндр разделён подвижным теплопроводным поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К, а аргона – 900 К; объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Поршень медленно перемещается без трения. Теплоёмкость поршня и цилиндра пренебрежимо мала. Чему равно отношение внутренней энергии гелия после установления теплового равновесия к его энергии в начальный момент?
Образец возможного решения
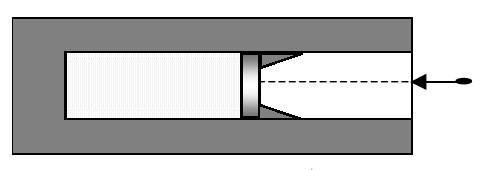
5. В вакууме
закреплен горизонтальный цилиндр с поршнем. В цилиндре находится
0,1 моль гелия. Поршень удерживается упорами и может скользить
влево вдоль стенок цилиндра без трения. В поршень попадает пуля
массой 10 г, летящая горизонтально со скоростью 400 м/с, и застревает
в нем. Температура гелия в момент остановки поршня в крайнем левом
положении возрастает на 64 К. Какова масса поршня? Считать, что
за время движения поршня газ не успевает обменяться теплом с поршнем
и цилиндром.
Образец возможного решения6. В горизонтальном цилиндрическом сосуде,
закрытом поршнем, находится одноатомный идеальный газ. Первоначальное
давление газа p1 = 4•105
Па. Расстояние от дна сосуда до поршня равно L. Площадь
поперечного сечения поршня S = 25 см2. В
результате медленного нагревания газ получил количество теплоты
Q = 1,65 кДж, а поршень сдвинулся на расстояние x
= 10 см. При движении поршня на него со стороны стенок сосуда
действует сила трения величиной Fтр = 3•103
Н. Найдите L. Считать, что сосуд находится в вакууме.
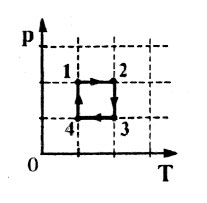
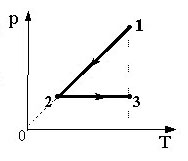
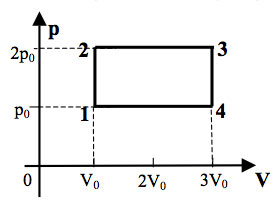
Образец возможного решения7. На pT-диаграмме показан
цикл тепловой машины, у которой рабочим телом является идеальный
газ (см. рисунок). На каком из участков цикла 1 – 2, 2 – 3, 3
– 4, 4 – 1 работа газа наибольшая по модулю?
Образец возможного решения
8. 10 моль одноатомного идеального
газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели
до первоначальной температуры 300 К (см. рисунок). Какое количество
теплоты получил газ на участке 2 – 3?
Образец возможного решения
9. 10 моль идеального одноатомного газа охладили,
уменьшив давление в 3 раза. Затем газ нагрели до первоначальной
температуры 300 К (см. рисунок). Какое количество теплоты сообщено
газу на участке 2 – 3?
Образец возможного решения
10. 1 моль идеального одноатомного газа сначала
охладили, а затем нагрели до первоначальной температуры 300
К, увеличив объем газа в 3 раза (см. рисунок). Какое количество
теплоты отдал газ на участке 1 – 2?
Образец возможного решения
10*. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А12 = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A31| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Qхол|, отданное газом за цикл холодильнику.
Образец возможного решения
11. Рассчитайте КПД тепловой
машины, использующей в качестве рабочего тела одноатомный идеальный
газ и работающей по циклу, изображенному на рисунке.
Образец возможного решения
Избранные задачи прошлых лет (с ответами)
12. Вертикально расположенный
замкнутый цилиндрический сосуд высотой 50 см разделен подвижным
поршнем весом 110 Н на две части, в каждой из которых содержится
одинаковое количество идеального газа при температуре 361 К. Сколько
молей газа находится в каждой части цилиндра, если поршень находится
на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.
13. В калориметре
находился лед при температуре t1 = – 5 °С.
Какой была масса m1 льда, если после добавления
в калориметр m2 = 4 кг воды, имеющей температуру
t2 = 20 °С, и установления теплового равновесия
температура содержимого калориметра оказалась равной t
= 0 °С, причем в калориметре была только вода?14. Теплоизолированный
цилиндр разделен подвижным теплопроводным поршнем на две части.
В одной части цилиндра находится гелий, а в другой — аргон. В
начальный момент температура гелия равна 300 К, а аргона — 900
К. При этом объемы, занимаемые газами одинаковы. Какую температуру
будут иметь газы в цилиндре после установления теплового равновесия,
если поршень перемещается без трения? Теплоемкостью сосуда и поршня
пренебречь.15. Теплоизолированный
сосуд объемом V = 2 м3 разделен теплопроводящей
перегородкой на две части одинакового объема. В одной части находится
m = 1 кг гелия, а в другой части m = 1 кг аргона.
Средняя квадратичная скорость атомов аргона равна средней квадратичной
скорости атомов гелия и составляет υ = 500 м/с. Рассчитайте
парциальное давление гелия после удаления перегородки.16. Теплоизолированный
сосуд объемом V = 2 м3 разделен пористой перегородкой
на две равные части. В начальный момент в одной части сосуда находится
νHe = 2 моль гелия, а в другой – νAr
= 1 моль аргона. Температура гелия ТHe = 300
К, а температура аргона ТAr = 600 К. Атомы
гелия могут свободно проникать через поры в перегородке, а атомы
аргона – нет. Определите температуру гелия после установления
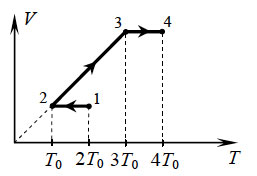
теплового равновесия в системе.17. С одним молем идеального
одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке
в координатах V-Т. Во сколько раз количество теплоты,
полученное газом в процессе 1-2-3-4 больше работы газа в этом
процессе?
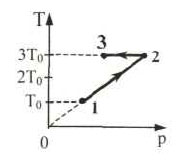
18. Один моль одноатомного
идеального газа совершает процесс 1-2-3 (см. рисунок). На участке
2 – 3 к газу подводят 3 кДж теплоты. Т0 =
100 К. Найдите отношение работы, совершаемой газом в ходе всего
процесса А123, к соответствующему полному
количеству подведенной к нему теплоты Q123.
19. Один моль идеального
одноатомного газа сначала изотермически сжали (Т1
= 300 К). Затем газ изохорно охладили, понизив давление в 3 раза
(см. рисунок). Какое количество теплоты отдал газ на участке 2
– 3?
20. Идеальный одноатомный
газ расширяется сначала адиабатно, а затем изобарно. Конечная
температура газа равна начальной (см. рисунок). За весь процесс
1-2-3 газом совершается работа, равная 5 кДж. Какую работу совершает
газ при адиабатном расширении?
21. На рисунке в координатах
p,T показан цикл тепловой машины, у которой
рабочим телом является идеальный газ. На каком участке цикла работа
газа наименьшая по модулю?
22. Один моль одноатомного
идеального газа совершает цикл, изображенный на pV-диаграмме
(см. рисунок). Участок 1 – 2 –– изотерма, 2 – 3 –?