Решение задач в сосуде полностью
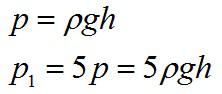
В последнее время мы разбирали решения многих простейших физических задач по разным темам: законы Ньютона, сила трения, свободное падение и т.д. Пришла пора взяться за что-то посложнее. Сегодня решаем задачи по теме «гидростатика».
За полезными лайфхаками и новостями студенческой жизни добро пожаловать на наш телеграм-канал.
Задачи по гидростатике с решениями
Задача №1 на гидростатику
Условие
B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает?
Решение
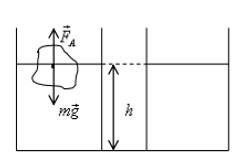
По условию плавания тел:
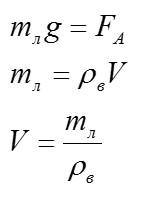
V – объем погруженной в воду части льда. После таяния льда образуется объем воды:
Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.
Ответ: уровень не изменится.
Задача №2 на гидростатику
Условие
Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?
Решение
Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:
Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:
В одном кубическом метре – тысяча литров.
Ответ: 2 литра.
Задача №3 на гидростатику
Условие
Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.
Решение
Вспоминаем основное уравнение гидростатики и записываем:
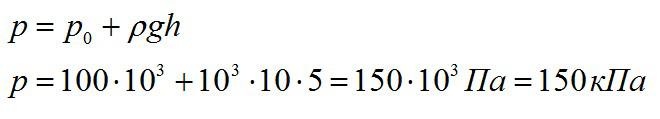
Ответ: 150 кПа.
Задача №4 на гидростатику
Условие
Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.
Решение
Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.
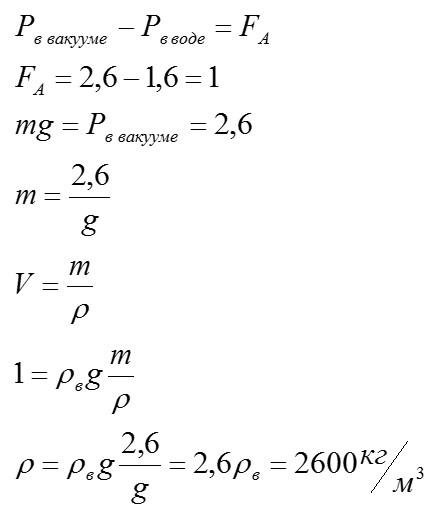
Ответ: 2600 кг/м3.
Задача №5 на гидростатику
Условие
Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?
Решение
Формула для гидростатического давления:
Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.
Ответ: высота увеличилась в 5 раз.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы по гидростатике
Вопрос 1. Что такое гидростатический парадокс?
Ответ. Гидростатический парадокс – явление, когда вес жидкости в сосуде не совпадает с весовым давлением, которое она оказывает на стенки сосуда. Возникает в сосудах конусообразной формы.
Вопрос 2. Какие есть внесистемные единицы изменения давления:
Ответ. Внесистемные единицы давления:
- миллиметр ртутного столба;
- бар;
- атмосфера.
Вопрос 3. В условиях физических задач часто можно встретить формулировку «нормальные условия». Что этот значить?
Ответ. Это значит, что давление нужно брать равным 101325 Па (или 760 мм рт. ст.), а температуру – 0 градусов Цельсия (или 273 Кельвина).
Вопрос 4. Что такое сообщающиеся сосуды?
Ответ. Сообщающиеся сосуды – это емкости, соединенные между собой. Жидкость может свободно перетекать из одного сосуда в другой. Уровень жидкости с одной плотностью в сообщающихся сосудах всегда одинаков. Простейший пример сообщающихся сосудов: обычный чайник. Если мы нальем в него воду, уровень будет одинаковым как в носике, так и в основном объеме. Если же плотности жидкостей разные, то выше будет уровень той, у которой плотность меньше.
Вопрос 5. Что такое гидравлический пресс?
Ответ. Гидравлический пресс – устройство, в основе действия которого лежит закон Паскаля и принцип сообщающихся сосудов. Пресс состоит из двух соединённых и заполненных маслом цилиндров: узкого и широкого. При нажатии на поршень узкого цилиндра, широкий цилиндр получает во столько раз большее давление, во сколько раз площадь большего поршня больше площади меньшего поршня.
Гидростатика: немного теории
Гидростатика – раздел физики, изучающий равновесие жидкостей.
Равновесие жидкостей – очень важный раздел. Например, если вы выпили много пива, просто необходимо, чтобы оно находилось в равновесии. Но шутки в сторону! Какие фундаментальные понятия нужно знать, чтобы решать задачи по гидростатике?
Давление и плотность
Давление – физическая величина, равная отношению модуля силы, перпендикулярно действующей на поверхность, к площади этой поверхности.
Давление столба жидкости называют гидростатическим, а измеряется оно в Паскалях. Гидростатическое давление столба жидкости высотой h на дно сосуда рассчитывается по формуле:
Греческое «ро» – плотность жидкости. Плотность измеряется в килограммах на кубический метр и равна отношению массы тела к его объему.
Жидкость – изотропная среда. Это значит, что ее свойства одинаковы в любой ее точке.
Закон Паскаля и основное уравнение гидростатики
Давление, оказываемое на жидкость или газ передается в любую точку этой жидкости одинаково и во всех направлениях.
Это и есть закон Паскаля. Согласно ему, давление жидкости зависит только от плотности жидкости и высоты ее столба. На глубине h жидкость оказывает одинаковое давление как на дно, так и на стенки сосуда.
В данном случае р нулевое – давление столба воздуха (атмосферы), которое действует на жидкость.
В своей другой формулировке основное уравнение гидростатики показывает, что гидростатический напор является постоянной величиной для всего объема неподвижной жидкости. Здесь мы не будем останавливаться на этом понятии, так как оно изучается в курсе гидравлики.
Закон Архимеда и условия плавания тел
Закон Архимеда – еще одна важнейшая часть гидростатики. Он гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Тело плавает, если выталкивающая сила Архимеда больше действующей на него силы тяжести. Это же условие можно переписать, используя понятие плотности: тело будет плавать, если плотность жидкости больше, чем плотность тела.
Подробнее о законе Архимеда и фактах из жизни этого выдающегося античного инженера читайте в нашем отдельном материале.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис за качественным и быстрым объяснением.
Источник
Задачи на смеси и сплавы при первом знакомстве
с ними вызывают у учащихся общеобразовательных
классов затруднения. Самостоятельно справиться
с ними могут немногие.
Задачи на смеси и сплавы, ранее встречающиеся
практически только на вступительных экзаменах в
ВУЗы и олимпиадах, сейчас включены в сборник для
подготовки и проведения экзамена по алгебре за
курс основной школы (9 класс) под редакцией С.А.
Шестакова. Эти задачи, имеющие практическое
значение, являются также хорошим средством
развития мышления учащихся.
Трудности при решении этих задач могут
возникать на различных этапах:
- составления математической модели (уравнения,
системы уравнений, неравенства и т. п.; - решения полученной модели;
- анализа математической модели (по причине
кажущейся ее неполноты:не хватает уравнения в
системе и пр.).
Все сложности преодолимы при тщательном
анализе задачи. Этому способствуют чертежи,
схемы, таблицы и пр. Каждый учащийся сам для себя
делает вывод об уровне сложности той или иной
задачи и месте, где эта сложность возникает.
Основными компонентами в этих задачах
являются:
- масса раствора (смеси, сплава);
- масса вещества;
- доля (% содержание) вещества.
При решении большинства задач этого вида, с
моей точки зрения, удобнее использовать таблицу,
которая нагляднее и короче обычной записи с
пояснениями. Зрительное восприятие
определенного расположения величин в таблице
дает дополнительную информацию, облегчающую
процесс решения задачи и её проверки.
Урок по решению этих задач целесообразно
провести в ходе обобщающего повторения по
алгебре в конце 9 класса.
Цель урока :обобщение, углубление,
систематизация знаний, умений, навыков учащихся,
развитие творческих способностей учащихся.
Ход урока.
I ) Актуализация опорных знаний обучаемых.
С помощью таблицы повторить основные
теоретические сведения по данной теме. При этом
учащиеся составляют опорный конспект (или
используют “Приложение 1”,
где уже напечатаны основные теоретические
сведения, тексты задач и незаполненные таблицы к
задачам).
Теоретические сведения.
Пусть m г некоторого вещества
растворяется в М г воды, тогда
–
доля вещества в растворе;
–
доля воды в растворе;
· 100
% – концентрация раствора, или процентное
содержание вещества в растворе;
·
100% – процентное содержание воды в растворе;
При этом · 100 % + · 100% = 100%.
Примечание 1. Вместо воды можно брать любую
жидкость – основание, в которой можно растворить
то или иное вещество.
Примечание 2. С математической точки зрения
растворы, смеси, сплавы не отличаются друг от
друга. Поэтому доля или процентное содержание
одного вещества в растворе, смеси, сплаве
определяются по одному правилу.
Примечание 3. Вместо весовых мер веществ и
воды можно брать доли или части (mчи
Мч ).
II) Знакомство учащихся с текстом задач и
выделение основных компонентов в них.
Таблица для решения задач имеет следующий вид:
| Наименование веществ, растворов, смесей, сплавов | % содержание вещества (доля содержания вещества) | Масса раствора (смеси, сплава) | Масса вещества |
III) Решение задач.
Рассмотрим решения задач с применением
таблицы.
Задача 1. В сосуд содержащий 2 кг 80 % -го
водного раствора уксуса добавили 3 кг воды.
Найдите концентрацию получившегося раствора
уксусной кислоты.
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (кг) | Масса вещества (кг) |
| Исходный раствор | 80 % = 0,8 | 2 | 0,8·2 |
| Вода | – | 3 | – |
| Новый раствор | х % = 0,01х | 5 | 0,01х·5 |
Масса уксусной кислоты не изменилась, тогда
получаем уравнение:
0,01х·5 = 0,8·2
0,05х = 1,6
х = 1,6:0,05
х = 32
Ответ:концентрация получившегося раствора
уксусной кислоты равна 32 %.
Очень часто в жизни приходится решать
следующую задачу.
Задача 2.Сколько нужно добавить воды в
сосуд, содержащий 200 г 70 % -го раствора уксусной
кислоты, чтобы получить 8 % раствор уксусной
кислоты?
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (г) | Масса вещества (г) |
| Исходный раствор | 70 % = 0,7 | 200 | 0,7·200 |
| Вода | – | х | – |
| Новый раствор | 8 % = 0,08 | 200 + х | 0,08(200 + х) |
Анализируя таблицу, составляем уравнение :
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ :1,55 кг воды.
Задача 3. Смешали некоторое количество 12%
раствора соляной кислоты с таким же количеством
20 % раствора этой же кислоты. Найти концентрацию
получившейся соляной кислоты.
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (кг) | Масса вещества (кг) |
| I раствор | 12 % = 0,12 | у | 0,12у |
| II раствор | 20 % = 0,2 | у | 0,2у |
| Смесь | х % = 0,01х | 2у | 0,01х·2у |
Анализируя таблицу, составляем уравнение :
0,12у + 0,2у = 0,01х·2у
Получили уравнение с двумя переменными,
учитывая, что , имеем
0,32 = 0,02х
х = 16
Ответ :концентрация раствора 16 %.
Задача 4. Смешали 8кг 18 % раствора некоторого
вещества с 12 кг 8 % раствора этого же вещества.
Найдите концентрацию получившегося раствора.
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (кг) | Масса вещества (кг) |
| I раствор | 18 % = 0,18 | 8 | 0,18·8 |
| II раствор | 8 % = 0,08 | 12 | 0,08·12 |
| Смесь | х % = 0,01х | 20 | 0,01х·20 |
Уравнение для решения задачи имеет вид:
0,01х·20 = 0,18·8 + 0,08·12
0,2х = 2,4
х = 12
Ответ:концентрация раствора 12 %.
Задача 5 Смешав 40 % и 15 % растворы кислоты,
добавили 3 кг чистой воды и получили 20 % раствор
кислоты. Если бы вместо 3 кг воды добавили 3 кг 80 %
раствора той же кислоты, то получили бы 50 %-ый
раствор кислоты. Сколько килограммов 40 % -го и 15 %
растворов кислоты было смешано?
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (кг) | Масса вещества (кг) |
| I раствор | 40 % = 0,4 | х | 0,4х |
| II раствор | 15 % = 0,15 | у | 0,15у |
| Вода | – | 3 | – |
| Смесь I | 20 % = 0,2 | х + у +3 | 0,2(х + у +3) |
Получаем уравнение:0,4х + 0,15у = 0,2(х + у +3)
Выполним вторую операцию:
| I раствор | 40 % = 0,4 | х | 0,4х |
| II раствор | 15 % = 0,15 | у | 0,15у |
| Кислота | 80 % = 0,8 | 3 | 0,8·3 |
| Смесь II | 50 % = 0,5 | х + у +3 | 0,5(х + у +3) |
Итак, 0,4х + 0,15у + 0,8·3 = 0,5(х + у +3).
Для решения задачи получаем систему уравнений:
Решаем систему уравнений:
Ответ:3,4 кг 40 % кислоты и 1,6 кг 15 % кислоты.
Задача 6. Имеется три сосуда. В первый сосуд
налили 4 кг 70 % сахарного сиропа, а во второй – 6 кг
40 % сахарного сиропа. Если содержимое первого
сосуда смешать с содержимым третьего сосуда, то
получим в смеси 55 % содержание сахара, а если
содержимое второго сосуда смешать с третьим, то
получим 35 % содержание сахара. Найдите массу
сахарного в третьем сосуде сиропа и концентрацию
сахара в нем.
Решение.
| Наименование веществ, смесей | % содержание (доля) вещества | Масса раствора (кг) | Масса вещества (кг) |
| I сосуд | 70 % = 0,7 | 4 | 0,7·4=2,8 |
| II сосуд | 40 % = 0,4 | 6 | 0,4·6 = 2,4 |
| III сосуд | у % = 0,01у | х | 0,01ху |
| I и III сосуды | 55 % = 0,55 | 4+х | 0,55(4+х) или 2,8+0,01ху |
| II и III сосуды | 35 % = 0,35 | 6+х | 0,35(6+х) или 2,4+0,01ху |
Итак, получаем систему уравнений :
Решаем её:
Ответ :1,5 кг сахарного сиропа 15 % концентрации.
Задача 7. Имеются два сплава, состоящие из
золота и меди. В первом сплаве отношение масс
золота и меди равно 8 :3, а во втором – 12 :5. Сколько
килограммов золота и меди содержится в сплаве,
приготовленном из 121 кг первого сплава и 255 кг
второго сплава?
Решение.
| Наименование веществ, смесей | Доля вещества | Масса сплава (кг) | Масса вещества (кг) | |||
| золото | медь | всего | Золото Мз | медь Мм | ||
| I сплав | 8 | 3 | 11 | 121 | ·121 | ·121 или 121- Мз |
| II сплав | 12 | 5 | 17 | 255 | ·255 | 255- Мз |
| III сплав | – | – | – | 376 | Сумма I и II сплавов | Сумма I и II сплавов |
·121
= 88 (кг) – масса золота в I сплаве
·255
= 180 (кг) масса золота в II сплаве
121+255=376 (кг) – масса III сплава
88+180=268 (кг) -масса золота в III сплаве
376-268=108 (кг) масса меди в III сплаве
Ответ :268 кг золота и 108 кг меди.
Задача 8. Одна смесь содержит вещества А и В
в отношении 4 :5, а другая смесь содержит те же
вещества, но в отношении 6 :7. Сколько частей
каждой смеси надо взять, чтобы получить третью
смесь, содержащую те же вещества в отношении 5 :6.
По условию задачи А :В = 5 :6, тогда
В данном случае получилось одно уравнение с
двумя переменными.
Решаем уравнение относительно .
Получим =.
Ответ : 9 частей первой смеси и 13 частей второй
смеси.
Задача 9.Из полного бака, содержащего 256 кг
кислоты, отлили п кг и долили бак водой.
После тщательного перемешивания отлили п
кг раствора и снова долили бак водой. После того
как такая процедура была проделана 8 раз, раствор
в баке стал содержать 1 кг кислоты. Найдите
величину п.
Решение.
В этой задаче важно правильно определить и
сохранить вид отдельных выражений – количество
кислоты и долю кислоты в растворах, чтобы выявить
закономерность.
Кроме того это должно тренировать и закреплять
соответствующие модели отдельных бытовых
действий.
Составляем уравнение для решения задачи :
=1
=
1
256-n= 27
n = 128
Ответ :n = 128.
IV) Домашнее задание: составить и решить не
менее двух задач на “растворы, смеси и сплавы”.
V ) Итоги урока.
Заключение.
Решение задач на “растворы, смеси и сплавы”
являются хорошим накоплением опыта решения
задач. В заключении очень полезно дать учащимся
составить свои задачи. При этом получаются
задачи и не имеющие решения, это позволяет им
моделировать реальные ситуации и процессы в
жизни. Такой вид работы делает мышление учащихся
оперативным, воспитывает творческое отношение к
тем задачам, которые ставит жизнь, учит учащихся
прогнозированию.
В задачах этого типа прослеживается системный
подход к решению задач. Происходит успешная
отработка и закрепление интеллектуальных умений
(анализ, синтез, аналогия, обобщение.
конкретизация и т.д.).
Опыт показал, что учащиеся не знавшие вначале,
как подойти к решению этих задач, в конце успешно
решали и составляли сами задачи.
Литература:
Крамор В.С., Лунгу К.Н. “Повторяем и
систематизируем школьный курс алгебры”, часть I.
– М.:Аркти, 2001.
Источник
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
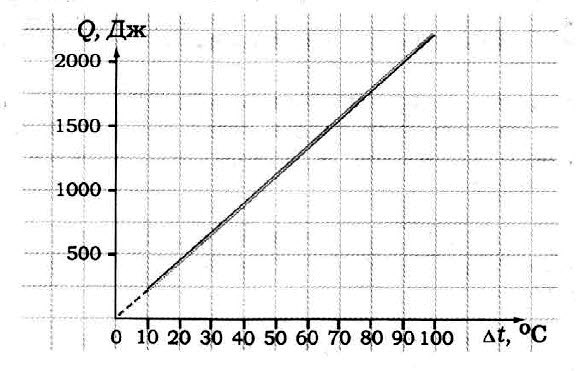

Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
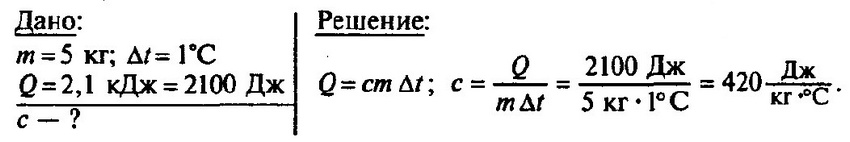
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Задача № 14. (повышенной сложности)
Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Источник
