Решение задачи про сообщающиеся сосуды

Из-за перепадов высот реки имеют разные глубины, что затрудняет или даже делает невозможным движение по ним судов. Поэтому строят шлюзы, которые рассчитывают по принципу сообщающихся сосудов. Формулы, используемые для вычислений, были получены в результате теоретического анализа, а после подтверждены экспериментально. Эти правила применяют при строении фонтанов, гидравлических прессов, плотин и различных устройств.

Общие сведения
В древние времена перед человечеством возникла проблема доставки воды в свои жилища. Так появились акведуки, а после и водопроводные трубы, канализация. В те времена механизмы ещё не были придуманы, поэтому задача решалась с помощью природных сил. Суть изобретений заключалась в организации самотёка жидкости за счёт изменения высот желобов и труб.
Использование таких систем хоть и позволяло справляться с поставленной задачей, но приносило определённые неудобства. Работа трубопроводов заключалась в использовании свойств жидкости перетекать из одного места в другое за счёт изменения оказываемого давления.
В 1684 году Паскаль продемонстрировал парадокс. Для этого он использовал:
- закрытую бочку с водой;
- герметичную трубку;
- кружку.

Его опыт заключался в следующем. Один конец трубки был вставлен в бочку, а второй вертикально поднят на высоту порядка шести метров. В свободный конец Паскаль вылил кружку воды. Из-за малого диаметра трубки вода стала подниматься, а бочка лопнула. Как оказалось, в середине ёмкости создалось большое давление, привёдшее к её повреждению.
Этот парадокс объясняется законом Архимеда. Он гласит, что на тело, погруженное в воду, действует выталкивающая сила, равная весу жидкости. Значит, тело не сможет плавать в ней. Но это ошибочное рассуждение. Так как на самом деле архимедова сила появляется из-за гидростатического давления, зависящего от размера водяного столба, а не веса воды.
Поэтому тело и может находиться на поверхности резервуара, если его масса будет меньше веса воды. Это возможно, когда резервуар ненамного превышает размеры физического тела. Например, судно не тонет в ограниченном доке, так же как в и открытом океане, несмотря на то что масса воды между плавающим средством и стенами порта может быть меньше, чем вес корабля.
Закон Паскаля описывается формулой давления: P = F / S, где:
- p — давление;
- F — приложенная сила;
- S — площадь поверхности сосуда.
Из выражения следует, что увеличение силы на стенки удерживающие возрастает пропорционально. Давление принято изменять в ньютонах на квадратный метр или в паскалях. Этот закон нашёл применение в тормозных системах, гидравлических прессах.
Условие равновесия
Пусть имеются два сосуда, при этом они могут иметь разную форму и размеры. В нижней части они сообщаются, то есть соединяются с помощью трубки, которая имеет запорный вентиль. Ёмкость, стоящую слева, удобно обозначить цифрой один, соответственно, с правой стороны — два. В первую колбу можно налить жидкость, высота столба которой составляет h1. Её плотность пусть будет равняться p1. Во втором сосуде налито другое вещество с плотностью p и расстоянием от поверхности до дна h2.

Можно предположить, что высоты столбов подобраны так, что при открытии крана движение водного раствора не произойдёт. То есть он не будет перетекать из одной ёмкости в другую. Это важно для рассуждений, так как в другом случае жидкости просто перемешаются. Поэтому пусть растворы находятся в состоянии равновесия. Значит, давление и в первом, и во втором сосудах в нижних точках трубки будет одинаковым.
Действительно, если представить, что вместо крана стоит лёгкая перегородка, то для того, чтобы она осталась на своём месте, давление с её двух сторон должно быть скомпенсировано. Другими словами, в системе должны действовать одинаковые силы.
Так как растворы находятся в равновесии, то можно записать: P1 = P2. Давление можно выразить через плотность и высоту столба. Для рассматриваемого случая оно будет гидростатическим. Определяют его по формуле: p = ρ * g * h, где:
- ρ — плотность искомой жидкости;
- g — ускорение свободного падения;
- h — высота столба.
Полученное равенство справедливо как для первой, так и второй ёмкости. Его можно подставить в равенство равновесия: ρ1 * g * h1 = ρ2 * g * h2. После того как левую и правую часть сократить на g, формула примет вид: ρ1 * h1 = ρ2 * h2. Последнее выражение для сообщающихся сосудов и описывает условие равновесия.

Теперь можно рассмотреть частный случай, когда обе ёмкости заполнены однородной жидкостью. Это означает, что ρ1 = ρ2 = ρ. Условие равновесия примет вид: ρh1 = ρh2. Выражение можно сократить на плотность. Отсюда следует, что h1 = h2. Найденное правило называют математическим действием закона сообщающихся сосудов.
Опираясь на выведенную формулу, можно сформулировать закон словами. Но для этого нужно вспомнить, что такое h1 и h2. По сути, это расстояние от свободной поверхности жидкости, рассчитываемое по вертикали. Отсюда следует определение, что свободные поверхности однородной жидкости в соединённых ёмкостях устанавливаются на одинаковой высоте.
Опыт на сообщение
Чтобы открыть свой закон, Паскалю понадобилось использовать для опытов только два сосуда. Всё дело в том, что, согласно формуле, на установившийся уровень жидкости не влияет форма, размер, масса и другие характеристики. Если они сообщающиеся, то высота столба во всех ёмкостях будет одинаковой.

Для того чтобы самостоятельно убедиться в действии закона, можно провести простой эксперимент. Понадобится взять два любых шприца, наполнить один из них водой и соединить с другим трубочкой. Затем поднять их на любой уровень и убедиться, что водяная линия столбов будет находиться в одной горизонтали. Причём она не изменится даже при наклоне сосудов.
Проведённый опыт не будет называться полным, если не провести эксперимент с разными жидкостями. Так, если налить растворы с отличающейся плотностью, то можно наблюдать, что водяной столб не сможет выровняться.
Например, такое явление особо заметно, если попробовать смешать раствор поваренной соли и воды. Интересно то, что высота столба будет настолько меньше, насколько отличается плотность.
Решение примеров
В школе после рассмотрения темы преподаватель часто предлагает школьникам написать реферат или подготовить небольшое сообщение для видеоурока. В таком докладе, кроме теории, рекомендуется приводить несколько задач. Их решение желательно сопровождать рисунками, чтобы наглядно продемонстрировать в проекте, как работают сообщающиеся сосуды.
Физики обычно демонстрируют полезность явления на следующих двух примерах:

- Труба с площадью сечения S погружена в чашу со ртутью на одну треть. Не изменяя положение нижнего конца трубки, её наклон изменили на угол j. Определить, как поменялась высота. Если принять размер столба ртути за h, то, зная площадь сечения трубки, можно вычислить объём жидкости: V = S * h. Длину, которую занимает жидкость, можно определить так: l = h / cos (j). Значит, объём будет равняться: V1 = S * l = (S * h) / cos (j). Отсюда возможно определить изменение объёма в трубке: ΔV = V1 — V = (S * h) / c o s (j) — S * h. Так как площадь ёмкости равняется: S = π * D2 / 4, то искомая высота составит: Δh = Δ V * S = 4 * S * h * (1 − cos (j) / cos (j) * π * D 2 ).
- Какой площадью нужно изготовить отливной поршень в водяном прессе, чтобы выигрыш был в шесть раз? Площадь большого рычага равна двум метрам. Рассматриваемая система есть не что иное, как гидравлический пресс. То есть это два сообщающихся сосуда. Если принять, что большему поршню S соответствует сил F, а меньшему — S1 и F1, то по закону Паскаля они будут относиться друг к другу как F / S = F1 / S1. Из этого равенства можно выразить искомую площадь: S1 = F1 * S / F. Согласно условию: F1 / F = 6. Значит, расчётная формула примет вид: S = S * n = 2 * 6 = 12.
Даже не заглядывая в Википедию, можно привести множество примеров использования свойства как в быту, так и в природе. Например, перелив в ванной, поилка для домашних птиц, различные устройства полива, чайник, фонтаны, шлюзы. В работе всех этих вещей используется закон для сообщающихся сосудов. Но самый простой пример — это применяемый в строительстве водяной уровень. Причём его конструкция настолько проста, что повторить её сможет любой даже в домашних условиях.
Источник
Продолжаем подготовку к олимпиадам. Тема сегодняшней статьи – сообщающиеся сосуды и сила Архимеда. Начнем, как обычно, со стартовых, более простых задач, и потом перейдем к тем, что посложнее. Интересное будет дальше…
Задача 1. В цилиндрических сообщающихся сосудах находится вода. Площадь поперечного сечения широкого сосуда в 4 раза больше площади поперечного сечения узкого сосуда. В узкий сосуд наливают керосин, который образует столб высотой 20 см. На сколько повысится уровень воды в широком сосуде и опустится в узком?

Рисунок 1
Сначала запишем условие несжимаемости:
На уровне однородной жидкости можно записать условие равенства давлений:
Тогда
Ответ: 3,2 см, 12,8 см.
Задача 2. Три одинаковых сообщающихся цилиндра частично заполнены водой. Когда в левый цилиндр налили слой керосина высотой см, а в правый высотой см, то уровень воды в среднем сосуде повысился. На сколько?

Рисунок 2
Условие несжимаемости:
Откуда
Теперь условие равновесия:
Откуда
Тогда можно подставить все в первое уравнение:
Или
Ответ: 12 см.
Задача 3. В сосуде с водой плавает деревянная дощечка с приклеенным сверху железным шариком. Изменится ли уровень воды в сосуде, если дощечку перевернуть шариком вниз?
Здесь мы познакомимся с методом решения задач такого типа серез силы, действующие на дно. Метод заключается в том, чтобы записать условие равновесия сил, действующих на дно сосуда до изменений и после них. Например, пусть в сосуде плавает кусок льда. Во-первых, полезно знать, что его масса равна массе воды, которую он вытеснил:

Рисунок 3
Сила, действующая на дно, с одной стороны:
Где – масса всего содержимого стакана (воды и льда).
С другой стороны,
Теперь лед растаял. Запишем новое условие равновесия сил, действующих на дно:
Масса содержимого не изменилась, поэтому
И
Теперь вернемся к задаче. Рассуждая таким же способом, заключаем, что после перевороте дощечки массы содержимых до переворота и после одинаковые, следовательно, уровень воды не изменится.
Задача 4. В стакане плавает кусок льда с вмороженной в него свинцовой дробинкой. Как изменится уровень воды, когда весь лед растает?
Запишем силу на дно в первом случае:
Когда лед растает, дробинка утонет, и будет давить на дно с силой
Для второго случая (масса содержимого не изменилась)
Но изменилась сила, действующая на дно:
Тогда
Так как правая часть, очевидно, положительное число, то , то есть уровень понизился.
Задача 5. В стакане с пресной водой плавает кусок дерева, к которому приклеен кусочек сахара. Как изменится уровень воды в стакане, когда сахар растворится?
Записываем силу на дно в первом случае:
Во втором случае
Масса содержимого не изменилась, следовательно,
Или
И плотность после растворения сахара стала больше, значит, уровень понизится.
Задача 6. Цилиндрическую гирю, подвешенную к динамометру, опускают в воду, пока показание динамометра не изменится на Н. На сколько изменится уровень воды в сосуде, если сечение сосуда S = 25 см?
Показания динамометра изменятся ровно на силу Архимеда:
Записываем силы на дно сначала:
После погружения гири сила давления на дно изменилась:
Тогда
Откуда
Ответ: на 4 см.
Источник
В последнее время мы разбирали решения многих простейших физических задач по разным темам: законы Ньютона, сила трения, свободное падение и т.д. Пришла пора взяться за что-то посложнее. Сегодня решаем задачи по теме «гидростатика».
За полезными лайфхаками и новостями студенческой жизни добро пожаловать на наш телеграм-канал.
Задачи по гидростатике с решениями
Задача №1 на гидростатику
Условие
B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает?
Решение
По условию плавания тел:
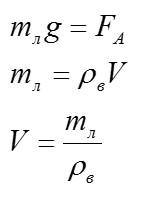
V – объем погруженной в воду части льда. После таяния льда образуется объем воды:
Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.
Ответ: уровень не изменится.
Задача №2 на гидростатику
Условие
Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?
Решение
Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:
Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:
В одном кубическом метре – тысяча литров.
Ответ: 2 литра.
Задача №3 на гидростатику
Условие
Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.
Решение
Вспоминаем основное уравнение гидростатики и записываем:
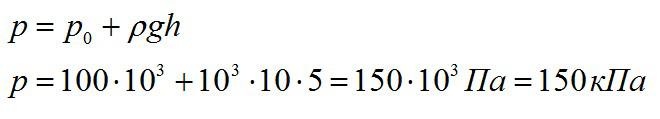
Ответ: 150 кПа.
Задача №4 на гидростатику
Условие
Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.
Решение
Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.
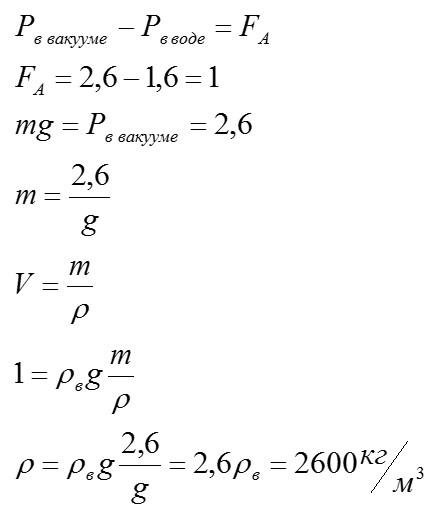
Ответ: 2600 кг/м3.
Задача №5 на гидростатику
Условие
Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?
Решение
Формула для гидростатического давления:
Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.
Ответ: высота увеличилась в 5 раз.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы по гидростатике
Вопрос 1. Что такое гидростатический парадокс?
Ответ. Гидростатический парадокс – явление, когда вес жидкости в сосуде не совпадает с весовым давлением, которое она оказывает на стенки сосуда. Возникает в сосудах конусообразной формы.
Вопрос 2. Какие есть внесистемные единицы изменения давления:
Ответ. Внесистемные единицы давления:
- миллиметр ртутного столба;
- бар;
- атмосфера.
Вопрос 3. В условиях физических задач часто можно встретить формулировку «нормальные условия». Что этот значить?
Ответ. Это значит, что давление нужно брать равным 101325 Па (или 760 мм рт. ст.), а температуру – 0 градусов Цельсия (или 273 Кельвина).
Вопрос 4. Что такое сообщающиеся сосуды?
Ответ. Сообщающиеся сосуды – это емкости, соединенные между собой. Жидкость может свободно перетекать из одного сосуда в другой. Уровень жидкости с одной плотностью в сообщающихся сосудах всегда одинаков. Простейший пример сообщающихся сосудов: обычный чайник. Если мы нальем в него воду, уровень будет одинаковым как в носике, так и в основном объеме. Если же плотности жидкостей разные, то выше будет уровень той, у которой плотность меньше.
Вопрос 5. Что такое гидравлический пресс?
Ответ. Гидравлический пресс – устройство, в основе действия которого лежит закон Паскаля и принцип сообщающихся сосудов. Пресс состоит из двух соединённых и заполненных маслом цилиндров: узкого и широкого. При нажатии на поршень узкого цилиндра, широкий цилиндр получает во столько раз большее давление, во сколько раз площадь большего поршня больше площади меньшего поршня.
Гидростатика: немного теории
Гидростатика – раздел физики, изучающий равновесие жидкостей.
Равновесие жидкостей – очень важный раздел. Например, если вы выпили много пива, просто необходимо, чтобы оно находилось в равновесии. Но шутки в сторону! Какие фундаментальные понятия нужно знать, чтобы решать задачи по гидростатике?
Давление и плотность
Давление – физическая величина, равная отношению модуля силы, перпендикулярно действующей на поверхность, к площади этой поверхности.
Давление столба жидкости называют гидростатическим, а измеряется оно в Паскалях. Гидростатическое давление столба жидкости высотой h на дно сосуда рассчитывается по формуле:
Греческое «ро» – плотность жидкости. Плотность измеряется в килограммах на кубический метр и равна отношению массы тела к его объему.
Жидкость – изотропная среда. Это значит, что ее свойства одинаковы в любой ее точке.
Закон Паскаля и основное уравнение гидростатики
Давление, оказываемое на жидкость или газ передается в любую точку этой жидкости одинаково и во всех направлениях.
Это и есть закон Паскаля. Согласно ему, давление жидкости зависит только от плотности жидкости и высоты ее столба. На глубине h жидкость оказывает одинаковое давление как на дно, так и на стенки сосуда.
В данном случае р нулевое – давление столба воздуха (атмосферы), которое действует на жидкость.
В своей другой формулировке основное уравнение гидростатики показывает, что гидростатический напор является постоянной величиной для всего объема неподвижной жидкости. Здесь мы не будем останавливаться на этом понятии, так как оно изучается в курсе гидравлики.
Закон Архимеда и условия плавания тел
Закон Архимеда – еще одна важнейшая часть гидростатики. Он гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
Тело плавает, если выталкивающая сила Архимеда больше действующей на него силы тяжести. Это же условие можно переписать, используя понятие плотности: тело будет плавать, если плотность жидкости больше, чем плотность тела.
Подробнее о законе Архимеда и фактах из жизни этого выдающегося античного инженера читайте в нашем отдельном материале.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис за качественным и быстрым объяснением.
Источник
Урок №51 Дата____________
Тема урока: Решение задач по теме «Сообщающие сосуды»
Тип урока: Урок формирования умений и навыков
Цели урока:
Развивающая: развитие аналитического чтения с целью глубокого осмысления содержания задачи с последующей записью её краткого условия; развитие логического мышления учащихся, навыков самостоятельной работы, коммуникативных способностей;
Обучающая: формирование умений решать комбинированные задачи по теме «Сообщающие сосуды».
Воспитательная: формирование умения выслушивать до конца и понять собеседника.
Оборудование и источники информации:
1. Исаченкова, Л.А. Физика: учеб. пособие для 7 кл. учреждений общ. сред. образования с рус.яз. обучения / Л.А. Исаченкова, Ю.Д. Лещинский; под ред. Л.А.Исаченковой. Минск: Народная асвета, 2017.-с.114-118.
2.Сборник задач по физике. 7 класс: пособие для учащихся учреждений общ. сред. образования с рус.яз. обучения / Ю.И.Гладков [и др.]. Минск: Аверсэв, 2016.-с.121-130.
3.Проектор,ЭСО «Наглядная физика. Введение».
Структура урока:
Организационный момент-1 мин.
Актуализация знаний-5 мин.
Основной этап урока-26 мин.
Физкультминутка-1 мин.
Закрепление знаний и умений-8 мин.
Рефлексия-2 мин.
Информация о домашнем задании- 2 мин.
1.Организационный момент.
-Здравствуйте! Садитесь.
Выявляем готовность класса к уроку. Проверяем выполнение домашнего задания, отвечаем на вопросы учащихся по домашнему заданию.
2.Актуализация знаний.
Актуализация знаний проводится в процессе диалога.
Используя модель «Двухкамерный шлюз» ЭСО «Наглядная физика. Введение», объясняем практическое применение закономерности, установленной для сообщающихся сосудов.
Подводя итоги первого этапа, ещё раз подчеркиваем, что уровни однородной жидкости в открытых покоящихся сосудах одинаковые.
3.Основной этап урока.
Решение задач в приложении 1.
Переходим к решению расчётных задач.
Задача №443 (Сб.)
В вертикальные открытые цилиндрические сообщающиеся сосуды, площади поперечных сечений которых различаются в n=4 раза, налита вода. Определите массу воды в широком сосуде, если вес воды в узком сосуде Р1=1,5 Н.
Задача упр.14 №3 (уч.)
Давление воды в кране водопроводной трубы, проходящей по дачному участку, p=200 кПа. Определите высоту от уровня крана до поверхности воды в баке водонапорной башни.
Задача № 448 (Сб.)
В две сообщающиеся цилиндрические трубки с разными диаметрами налита ртуть. В широкую трубку площадью поперечного сечения S=8,0см2 опустили деревянный брусок массой m=272 г. Определите разность уровней ртути в трубках.
4.Физкультминутка.
Раз, два, три , четыре,
Руки выше, руки шире.
Поворот направо, влево,
Всё мы делаем умело
Одну ногу поднимаем,
Этим площадь уменьшаем.
А давление растёт,
Прыгнем – вовсе пропадёт!
5.Закрепление знаний и умений.
Закрепление производим с помощью решения расчётной задачи.
Решение задачи в приложении 1.
Поверхность воды в водонапорной башне находится на h=40 м выше кухонного водопроводного крана. Определите давление воды в кране. Коэффициент g примите равным 10 .
6.Рефлексия.
Побуждаем учащихся к рефлексии.
На сколько % продвинулись в решении аналитических задач?
Учащиеся отвечают на вопрос рефлексии.
7.Информация о домашнем задании.
§32. Упр.14, №4-5
Источник
