Решение задачи сосуд с водой

Сосуды с водой I

Отмерьте ровно 4 литра, если у вас есть 3-литровая банка, 5-литровая банка и неограниченный доступ к воде.
Сосуды с водой II
Дано: 8-литровый сосуд, заполненный водой, и два пустых сосуда – объёмом 3 и 5 литров.
Как разделить воду на две равные части (4 и 4 литра), используя наименьшее количество переливаний?
Сосуды с водой III
Дано: 7-литровый сосуд, заполненный водой, и два пустых – объёмом 4 и 3 литра.
Поделите воду на 2, 2 и 3 литра, используя минимальное количество переливаний.
Сосуды с водой IV
Отмерьте 6 литров воды, используя 4 и 9-литровые сосуды.
Сосуды с водой V

Отмерьте 2 литра воды, используя:
1. 4 и 5-литровые сосуды;
2. 4 и 3-литровые сосуды.
Сосуды с водой VI
Даны 3 сосуда: сосуд А (8-литровый с 5-ю литрами воды); сосуд В (5-литровый с 3-мя литрами воды); и сосуд С (3-литровый с 2-мя литрами воды).
Отмерьте 1 литр, перелив воду только два раза.
Задача на взвешивание I

У вас 10 мешков с монетами, по 1000 монет в каждом. В одном из мешков все монеты фальшивые. Настоящая монета весит 1 г., фальшивая – 1,1 г.. Имея точные весы, как определить мешок с фальшивыми монетами с помощью только одного взвешивания?
Что если неизвестно, сколько мешков было с фальшивыми монетами?
Задача на взвешивание III
А эта задача ещё чуть посложнее предыдущей.
У вас есть 8 мешков с монетами по 48 монет в каждом. В пяти мешках настоящие монеты, а в остальных – фальшивые. С помощью одного взвешивания на точных весах определите все мешки с фальшивками, используя минимальное количество монет.
Задача на взвешивание IV

Один из 12-ти биллиардных шаров бракованный. Он весит или больше, или меньше, чем стандартный. У Вас есть чашечные весы-противовесы, на которых Вы можете сравнивать вес шаров.
Какое минимальное количество взвешиваний гарантирует нахождение бракованного шара?
Задача на взвешивание V
На рождественской ёлке висят три пары шаров: два белых, два голубых и два красных. Внешне шары одинакового размера. Однако в каждой паре есть один лёгкий и один тяжёлый шар. Все лёгкие шары весят между собой одинаково, и так же все тяжёлые шары. С помощью двух взвешиваний на чашечных весах определите все лёгкие и все тяжёлые шары.
Задача на взвешивание VI
Имеется девять мешков: восемь с песком и один – с золотом. Мешок с золотом только чуть тяжелее. Вам даётся два взвешивания на чашечных весах, чтобы найти мешок с золотом.
Задача на взвешивание VII
Имеется 27 теннисных шариков. 26 весят одинаково, а 27-й чуть потяжелее.
Какое минимальное количество взвешиваний на чашечных весах гарантирует нахождение тяжёлого шарика?
Задача на взвешивание VIII
Купец уронил 40-фунтовую гирю, и она раскололась на 4 неравные части. Когда эти части взвесили, то оказалось, что вес каждой из них (в фунтах) – целое число. Более того, с помощью этих частей можно было взвесить на чашечных весах любой вес (представляющий собой целое число) до 40 фунтов.
Сколько весила каждая часть?
Песочные часы I
![]()
![]()
Как отмерить 9 минут с помощью 7-минутных и 4-минутных песочных часов?
Песочные часы II
Учитель математики использовал необычный метод измерения времени, отведённого на экзамен. У него были 7-минутные и 11-минутные песочные часы. И чтобы отмерить 15 минут, он переворачивал часы только 3 раза. Объясните как.
(Примечание: одновременное переворачивание обоих часов можно считать за одно переворачивание.)
Бикфордовы шнуры
Имеется два огнепроводных шнура, каждый из которых сгорает ровно за час. Однако шнуры горят неравномерно – некоторые их части горят быстрее, а некоторые медленнее.
Как с помощью этих шнуров отмерить ровно 45 минут?
Девиз
Я не знаю каким оружием будут сражаться в 3-й мировой войне, но в 4-й мировой войне будут сражаться палками и камнями.
Альберт Эйнштейн
Источник
Условие задачи:
В сосуд с водой объемом 0,25 л при 20 °C поместили 50 г расплавленного свинца с температурой 350 °C. Какая температура установится в результате теплообмена в сосуде? Удельные теплоёмкости расплава и твёрдого свинца считать одинаковыми.
Задача №5.2.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(V_1=0,25) л, (t_1=20^circ) C, (m_2=50) г, (t_2=350^circ) C, (t-?)
Решение задачи:
Полностью аналогичная задача уже была представлена на сайте, правда в ней расплавленный свинец имел температуру 400 °C. Можете прорешать её после этой, дабы закрепить свои навыки.
В этой задаче нужно обязательно произвести оценку. Давайте для начала определим количество теплоты (Q_1), которое необходимо для нагревания воды массой (m_1) от температуры (t_1) до температуры кипения (t_к) ((t_к=100^circ) C). Это можно сделать по следующей формуле:
[{Q_1} = {c_1}{m_1}left( {{t_к} – {t_1}} right)]
Удельная теплоёмкость воды (c_1) равна 4200 Дж/(кг·°C).
Массу (m_1) представим как произведение плотности воды (rho) (она равна 1000 кг/м3) на объем (V_1), тогда:
[{Q_1} = {c_1}rho {V_1}left( {{t_к} – {t_1}} right)]
Посчитаем численное значение (Q_1) (объем при расчете мы перевели в кубические метры):
[{Q_1} = 4200 cdot 1000 cdot 0,25 cdot {10^{ – 3}} cdot left( {100 – 20} right) = 84000;Дж]
Так как температура расплавленного свинца (t_2) больше температуры его плавления (t_п) ((t_п=327^circ) C), то определим количество теплоты (Q_2), выделяемое при охлаждении расплава свинца от температуры (t_2) до температуры (t_п).
[{Q_2} = {c_2}{m_2}left( {{t_2} – {t_п}} right)]
Удельная теплоёмкость расплава свинца (и твёрдого свинца) (c_2) равна 130 Дж/(кг·°C).
[{Q_2} = 130 cdot 0,05 cdot left( {350 – 327} right) = 149,5;Дж]
Количество теплоты (Q_3), выделяемое при кристаллизации свинца массой (m_2), определим по формуле:
[{Q_3} = lambda {m_2}]
Удельная теплота кристаллизации (плавления) свинца (lambda) равна 25 кДж/кг.
[{Q_3} = 25 cdot {10^3} cdot 0,05 = 1250;Дж]
Количество теплоты (Q_4), выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t_к), равно:
[{Q_4} = {c_2}{m_2}left( {{t_п} – {t_к}} right)]
[{Q_4} = 130 cdot 0,05 cdot left( {327 – 100} right) = 1475,5;Дж]
Видно, что ({Q_1} > {Q_2} + {Q_3} + {Q_4}), значит температура теплового равновесия будет лежать в пределах от (t_1) до (t_к). Запишем уравнение теплового баланса:
[{Q_5} = {Q_2} + {Q_3} + {Q_6}]
Здесь (Q_5) – количество теплоты, необходимое для нагревания воды массой (m_1) от температуры (t_1) до температуры (t); (Q_6) – количество теплоты, выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t). Тогда:
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – {t_п}} right) + lambda {m_2} + {c_2}{m_2}left( {{t_п} – t} right)]
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – t} right) + lambda {m_2}]
Раскроем скобки:
[{c_1}{m_1}t – {c_1}{m_1}{t_1} = {c_2}{m_2}{t_2} – {c_2}{m_2}t + lambda {m_2}]
Все члены с множителем (t) перенесем в левую сторону, вынесем его за скобки, остальные перенесем в правую.
[tleft( {{c_1}{m_1} + {c_2}{m_2}} right) = {c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}]
[t = frac{{{c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}{m_1} + {c_2}{m_2}}}]
Массу (m_1) представим как произведение плотности воды (rho) на объем (V_1), как это уже было сделано выше:
[t = frac{{{c_1}rho {V_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}rho {V_1} + {c_2}{m_2}}}]
Переведём некоторые величины в систему СИ:
[0,25;л = 0,25 cdot {10^{ – 3}};м^3]
[50;г = 0,05;кг]
Численно температура (t) равна:
[t = frac{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} cdot 20 + 130 cdot 0,05 cdot 350 + 25 cdot {{10}^3} cdot 0,05}}{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} + 130 cdot 0,05}} = 23,2^circ;C = 296,7;К]
Ответ: 296,7 К.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
 задаÑи на пеÑеливание
задаÑи на пеÑеливаниеÐадаÑи на пеÑеливание водÑ
ÐÑи пÑоведении олимпиад по маÑемаÑике, оÑобенно в 6-Ñ ÐºÐ»Ð°ÑÑÐ°Ñ , воÑÑÑÐµÐ±Ð¾Ð²Ð°Ð½Ñ Ð·Ð°Ð´Ð°Ñи на пеÑеливание Ð²Ð¾Ð´Ñ Ð¸ дÑÑÐ³Ð¸Ñ Ð¶Ð¸Ð´ÐºÐ¾ÑÑей. Рданной ÑÑаÑÑе пÑиведен ÑÐ°Ð·Ð±Ð¾Ñ Ð½ÐµÑколÑÐºÐ¸Ñ Ð·Ð°Ð´Ð°Ñ Ñ Ð¸ÑполÑзованием маÑÑиÑ.
1. Ðожно ли Ð¸Ð¼ÐµÑ Ð´Ð²Ð° ÑоÑÑда емкоÑÑÑÑ 3 и 5 л, набÑаÑÑ Ð¸Ð· водопÑоводного кÑана 4 л водÑ?
РеÑение
1. ÐабиÑаем 5 лиÑÑов в пÑÑилиÑÑовÑй ÑоÑÑд,
2. Ðз пÑÑилиÑÑового ÑоÑÑда вливаем в ÑÑÐµÑ Ð»Ð¸ÑÑовÑй ÑÑи лиÑÑа, в пÑÑилиÑÑовом оÑÑаÑÑÑÑ Ð´Ð²Ð° лиÑÑа
3. Ðз ÑÑÐµÑ Ð»Ð¸ÑÑовой вÑливаем вÑе и оÑÑаеÑÑÑ 2 лиÑÑа в пÑÑилиÑÑовой.
4. Ðз пÑÑилиÑÑовой пеÑеливаем вÑе в ÑÑÐµÑ Ð»Ð¸ÑÑовÑÑ. РпÑÑилиÑÑовой 0 лиÑÑов в ÑÑÐµÑ Ð»Ð¸ÑÑовой 2 лиÑÑа.
5. ÐабиÑаем в пÑÑилиÑÑовÑÑ Ð¿ÑÑÑ Ð»Ð¸ÑÑов.
6. Ðз пÑÑилиÑÑовой пеÑеливаем лиÑÑ Ð² ÑÑÐµÑ Ð»Ð¸ÑÑовÑÑ.
7. ÐÑливаем 3 лиÑÑа из ÑÑÐµÑ Ð»Ð¸ÑÑовой и оÑÑаеÑÑÑ 4 лиÑÑа в пÑÑилиÑÑовой.
ÐаннÑй алгоÑиÑм ÑеÑÐµÐ½Ð¸Ñ Ð·Ð°Ð´Ð°Ñи можно изобÑазиÑÑ Ð² виде ÑаблиÑÑ
| 0 лиÑÑов | 0 лиÑÑов | 3 лиÑÑа | 0 лиÑÑов | 2 лиÑÑа | 2 лиÑÑа | 3 лиÑÑа | 0 лиÑÑов |
| 0 лиÑÑов | 5 лиÑÑов | 2 лиÑÑа | 2 лиÑÑа | 0 лиÑÑов | 5 лиÑÑа | 4 лиÑÑа | 4 лиÑÑа |
2. Ðак ÑазделиÑÑ Ð¿Ð¾ÑÐ¾Ð²Ð½Ñ Ð¼ÐµÐ¶Ð´Ñ Ð´Ð²ÑÐ¼Ñ ÑемÑÑми 12 л кваÑа , коÑоÑÑй Ð½Ð°Ñ Ð¾Ð´Ð¸ÑÑÑ Ð² 12-Ñи лиÑÑовом ÑоÑÑде, Ð´Ð»Ñ ÑÑого Ñ Ð²Ð°Ñ ÐµÑÑÑ 2 ÑоÑÑда 8-ми лиÑÑовÑй и 3-ÐµÑ Ð»Ð¸ÑÑовÑй.
РеÑение задаÑи на пеÑеливание
| 12л емкоÑÑÑ | 12л | 9л | 9л | 6л | 6л |
| 8л емкоÑÑÑ | 0л | 0л | 3л | 3л | 6л |
| 3л емкоÑÑÑ | 0л | 3л | 0л | 3л | 0л |
3. Ðидон емкоÑÑÑÑ 10 л наполнен кеÑоÑином. ÐмеÑÑÑÑ Ð¿ÑÑÑÑе ÑоÑÑÐ´Ñ Ð² 7 и 2 лиÑÑа. Ðак ÑазлиÑÑ ÐºÐµÑоÑин в два ÑоÑÑда по 5 лиÑÑов?
РеÑение
| 10л емкоÑÑÑ | 10л | 3л | 3л | 5л |
| 2л емкоÑÑÑ | 0л | 0л | 2л | 0л |
| 7л емкоÑÑÑ | 0л | 7л | 5л | 5л |
4. ÐÑÑÑ 2 ÑоÑÑда. ÐмкоÑÑÑ Ð¾Ð´Ð½Ð¾Ð³Ð¾ 9 л дÑÑгого 4л. Ðак Ñ Ð¸Ñ Ð¿Ð¾Ð¼Ð¾ÑÑÑ Ð¸Ð· бака набÑаÑÑ 6л водÑ? ÐÐ¾Ð´Ñ Ð¼Ð¾Ð¶Ð½Ð¾ ÑливаÑÑ Ð¾Ð±ÑаÑно в бак.
РеÑение
| 9л емкоÑÑÑ | 0л | 9л | 5л | 5л | 1л | 1л | 0л | 9л | 6л |
| 4лемкоÑÑÑ | 0л | 0л | 4л | 0л | 4л | 0л | 1л | 1л | 1л |
5. Ðак, Ð¸Ð¼ÐµÑ Ð´Ð²Ð° ÑоÑÑда емкоÑÑÑÑ 6л и 9л, набÑаÑÑ 3л водÑ?
РеÑение
| 0л | 0л | 5л | 0л | 4л | 4л | 5л | 0л | 5л | 0л |
| 0л | 9л | 4л | 4л | 0л | 9л | 8л | 8л | 3л | 3л |
ÐамеÑание. ÐодÑобное ÑеÑение пÑиведено ÑолÑко в пеÑвом ÑлÑÑае. РпоÑÐ»ÐµÐ´Ð½Ð¸Ñ Ð¿ÑÐ¸Ð²ÐµÐ´ÐµÐ½Ñ ÑолÑко ÑаблиÑÑ. ÐадеÑÑÑ Ñ Ð¿Ð¾Ð¼Ð¾ÑÑÑ Ð¸Ñ Ð»ÐµÐ³ÐºÐ¾ воÑÑÑанавливаеÑÑÑ ÑеÑение Ð·Ð°Ð´Ð°Ñ Ð½Ð° пеÑеливание.
Источник
В последнее время мы разбирали решения многих простейших физических задач по разным темам: законы Ньютона, сила трения, свободное падение и т.д. Пришла пора взяться за что-то посложнее. Сегодня решаем задачи по теме «гидростатика».
За полезными лайфхаками и новостями студенческой жизни добро пожаловать на наш телеграм-канал.
Задачи по гидростатике с решениями
Задача №1 на гидростатику
Условие
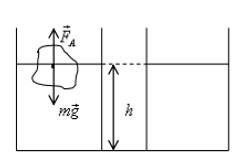
B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает?
Решение
По условию плавания тел:
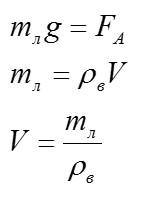
V – объем погруженной в воду части льда. После таяния льда образуется объем воды:
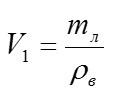
Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.
Ответ: уровень не изменится.
Задача №2 на гидростатику
Условие
Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?
Решение
Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:
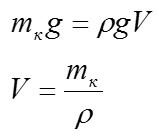
Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:
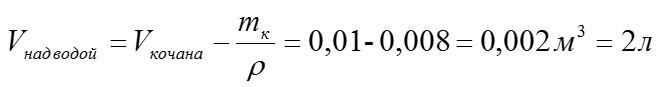
В одном кубическом метре – тысяча литров.
Ответ: 2 литра.
Задача №3 на гидростатику
Условие
Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.
Решение
Вспоминаем основное уравнение гидростатики и записываем:
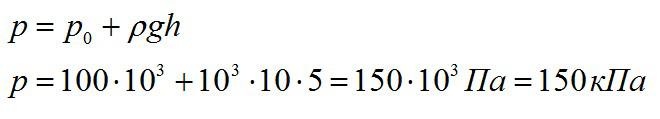
Ответ: 150 кПа.
Задача №4 на гидростатику
Условие
Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.
Решение
Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.
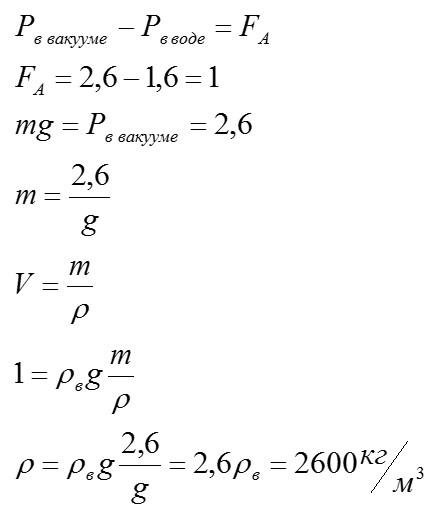
Ответ: 2600 кг/м3.
Задача №5 на гидростатику
Условие
Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?
Решение
Формула для гидростатического давления:
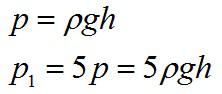
Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.
Ответ: высота увеличилась в 5 раз.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы по гидростатике
Вопрос 1. Что такое гидростатический парадокс?
Ответ. Гидростатический парадокс – явление, когда вес жидкости в сосуде не совпадает с весовым давлением, которое она оказывает на стенки сосуда. Возникает в сосудах конусообразной формы.
Вопрос 2. Какие есть внесистемные единицы изменения давления:
Ответ. Внесистемные единицы давления:
- миллиметр ртутного столба;
- бар;
- атмосфера.
Вопрос 3. В условиях физических задач часто можно встретить формулировку «нормальные условия». Что этот значить?
Ответ. Это значит, что давление нужно брать равным 101325 Па (или 760 мм рт. ст.), а температуру – 0 градусов Цельсия (или 273 Кельвина).
Вопрос 4. Что такое сообщающиеся сосуды?
Ответ. Сообщающиеся сосуды – это емкости, соединенные между собой. Жидкость может свободно перетекать из одного сосуда в другой. Уровень жидкости с одной плотностью в сообщающихся сосудах всегда одинаков. Простейший пример сообщающихся сосудов: обычный чайник. Если мы нальем в него воду, уровень будет одинаковым как в носике, так и в основном объеме. Если же плотности жидкостей разные, то выше будет уровень той, у которой плотность меньше.
Вопрос 5. Что такое гидравлический пресс?
Ответ. Гидравлический пресс – устройство, в основе действия которого лежит закон Паскаля и принцип сообщающихся сосудов. Пресс состоит из двух соединённых и заполненных маслом цилиндров: узкого и широкого. При нажатии на поршень узкого цилиндра, широкий цилиндр получает во столько раз большее давление, во сколько раз площадь большего поршня больше площади меньшего поршня.
Гидростатика: немного теории
Гидростатика – раздел физики, изучающий равновесие жидкостей.
Равновесие жидкостей – очень важный раздел. Например, если вы выпили много пива, просто необходимо, чтобы оно находилось в равновесии. Но шутки в сторону! Какие фундаментальные понятия нужно знать, чтобы решать задачи по гидростатике?
Давление и плотность
Давление – физическая величина, равная отношению модуля силы, перпендикулярно действующей на поверхность, к площади этой поверхности.
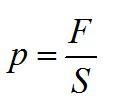
Давление столба жидкости называют гидростатическим, а измеряется оно в Паскалях. Гидростатическое давление столба жидкости высотой h на дно сосуда рассчитывается по формуле:
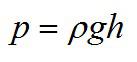
Греческое «ро» – плотность жидкости. Плотность измеряется в килограммах на кубический метр и равна отношению массы тела к его объему.
Жидкость – изотропная среда. Это значит, что ее свойства одинаковы в любой ее точке.
Закон Паскаля и основное уравнение гидростатики
Давление, оказываемое на жидкость или газ передается в любую точку этой жидкости одинаково и во всех направлениях.
Это и есть закон Паскаля. Согласно ему, давление жидкости зависит только от плотности жидкости и высоты ее столба. На глубине h жидкость оказывает одинаковое давление как на дно, так и на стенки сосуда.
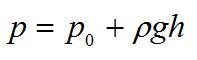
В данном случае р нулевое – давление столба воздуха (атмосферы), которое действует на жидкость.
В своей другой формулировке основное уравнение гидростатики показывает, что гидростатический напор является постоянной величиной для всего объема неподвижной жидкости. Здесь мы не будем останавливаться на этом понятии, так как оно изучается в курсе гидравлики.
Закон Архимеда и условия плавания тел
Закон Архимеда – еще одна важнейшая часть гидростатики. Он гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.
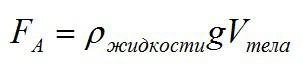
Тело плавает, если выталкивающая сила Архимеда больше действующей на него силы тяжести. Это же условие можно переписать, используя понятие плотности: тело будет плавать, если плотность жидкости больше, чем плотность тела.
Подробнее о законе Архимеда и фактах из жизни этого выдающегося античного инженера читайте в нашем отдельном материале.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис за качественным и быстрым объяснением.
Источник
Условие задачи:
В сосуд с водой объемом 0,25 л при 20 °C поместили 50 г расплавленного свинца с температурой 400 °C. Какая температура установится в результате теплообмена в сосуде? Удельные теплоёмкости расплава и твердого свинца считать одинаковыми.
Задача №5.2.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(V_1=0,25) л, (t_1=20^circ) C, (m_2=50) г, (t_2=400^circ) C, (t-?)
Решение задачи:
В этой задаче нужно обязательно произвести оценку. Давайте для начала определим количество теплоты (Q_1), которое необходимо для нагревания воды массой (m_1) от температуры (t_1) до температуры кипения (t_к) ((t_к=100^circ) C). Это можно сделать по следующей формуле:
[{Q_1} = {c_1}{m_1}left( {{t_к} – {t_1}} right)]
Удельная теплоёмкость воды (c_1) равна 4200 Дж/(кг·°C).
Массу (m_1) представим как произведение плотности воды (rho) (она равна 1000 кг/м3) на объем (V_1), тогда:
[{Q_1} = {c_1}rho {V_1}left( {{t_к} – {t_1}} right)]
Посчитаем численное значение (Q_1) (объем при расчете мы перевели в кубические метры):
[{Q_1} = 4200 cdot 1000 cdot 0,25 cdot {10^{ – 3}} cdot left( {100 – 20} right) = 84000;Дж]
Так как температура расплавленного свинца (t_2) больше температуры его плавления (t_п) ((t_п=327^circ) C), то определим количество теплоты (Q_2), выделяемое при охлаждении расплава свинца от температуры (t_2) до температуры (t_п).
[{Q_2} = {c_2}{m_2}left( {{t_2} – {t_п}} right)]
Удельная теплоёмкость расплава свинца (и твёрдого свинца) (c_2) равна 130 Дж/(кг·°C).
[{Q_2} = 130 cdot 0,05 cdot left( {400 – 327} right) = 474,5;Дж]
Количество теплоты (Q_3), выделяемое при кристаллизации свинца массой (m_2), определим по формуле:
[{Q_3} = lambda {m_2}]
Удельная теплота кристаллизации (плавления) свинца (lambda) равна 25 кДж/кг.
[{Q_3} = 25 cdot {10^3} cdot 0,05 = 1250;Дж]
Количество теплоты (Q_4), выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t_к), равно:
[{Q_4} = {c_2}{m_2}left( {{t_п} – {t_к}} right)]
[{Q_4} = 130 cdot 0,05 cdot left( {327 – 100} right) = 1475,5;Дж]
Видно, что ({Q_1} > {Q_2} + {Q_3} + {Q_4}), значит температура теплового равновесия будет лежать в пределах от (t_1) до (t_к). Запишем уравнение теплового баланса:
[{Q_5} = {Q_2} + {Q_3} + {Q_6}]
Здесь (Q_5) – количество теплоты, необходимое для нагревания воды массой (m_1) от температуры (t_1) до температуры (t); (Q_6) – количество теплоты, выделяемое при охлаждении свинца массой (m_2) от температуры (t_п) до температуры (t). Тогда:
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – {t_п}} right) + lambda {m_2} + {c_2}{m_2}left( {{t_п} – t} right)]
[{c_1}{m_1}left( {t – {t_1}} right) = {c_2}{m_2}left( {{t_2} – t} right) + lambda {m_2}]
Раскроем скобки:
[{c_1}{m_1}t – {c_1}{m_1}{t_1} = {c_2}{m_2}{t_2} – {c_2}{m_2}t + lambda {m_2}]
Все члены с множителем (t) перенесем в левую сторону, вынесем его за скобки, остальные перенесем в правую.
[tleft( {{c_1}{m_1} + {c_2}{m_2}} right) = {c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}]
[t = frac{{{c_1}{m_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}{m_1} + {c_2}{m_2}}}]
Массу (m_1) представим как произведение плотности воды (rho) на объем (V_1), как это уже было сделано выше:
[t = frac{{{c_1}rho {V_1}{t_1} + {c_2}{m_2}{t_2} + lambda {m_2}}}{{{c_1}rho {V_1} + {c_2}{m_2}}}]
Переведём некоторые величины в систему СИ:
[0,25;л = 0,25 cdot {10^{ – 3}};м^3]
[50;г = 0,05;кг]
Численно температура (t) равна:
[t = frac{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} cdot 20 + 130 cdot 0,05 cdot 400 + 25 cdot {{10}^3} cdot 0,05}}{{4200 cdot 1000 cdot 0,25 cdot {{10}^{ – 3}} + 130 cdot 0,05}} = 23,5^circ;C = 296,5;К]
Ответ: 296,5 К.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
