Решить задачу в одном сосуде

При решении задач на сплавы и смеси считают, что сумма масс сплавляемых веществ равна массе получаемого сплава, что сумма масс вещества, входящего в сплавы равна массе этого вещества в полученном сплаве. Аналогичное допущение принимаем и для сумм масс (объёмов) при смешивании жидкостей.
Рассмотрим подготовительную задачу.
Задача 1. Имеется уксусный раствор массой 1,5 кг, содержащий 40 % уксуса. Сколько килограммов воды нужно добавить в раствор, чтобы новый раствор содержал 10 % уксуса?
Решение. I способ.
1) 40 : 10 = 4 (раза) — во столько раз уменьшилась концентрация уксуса в растворе и увеличилась масса раствора,
2) 1,5 * 4 = 6 (кг) — масса нового раствора,
3) 6 – 1,5 = 4,5 (кг) — воды надо добавить.
II способ. 1) 0,4 * 1,5 = 0,6 (кг) — масса уксуса в первом растворе.
2) Пусть добавили x кг воды. Составим уравнение:
0,1(1,5 + x) = 0,6.
Оно имеет единственный корень 4,5. Значит, надо добавить 4,5 кг воды.
Ответ. 4,5 кг.
Рассмотрим способы решения задач на смеси и сплавы из сборников вариантов для подготовки к ЕГЭ.
Задача 2. (2017) В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Определите процентную концентрацию того же вещества в новом растворе.
Задача 3. (2018) Имеется два сплава. Первый содержит 25 % никеля, второй — 30 % никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 28 % никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение. Пусть масса первого сплава x кг, второго (150 – x) кг, третьего — 150 кг. Найдём массу никеля в каждом из трёх сплавов. Никеля было
в первом сплаве 0,25x кг,
во втором — 0,3(150 – x) кг,
в третьем — 0,28 *150 = 42 (кг).
Составим уравнение:
0,25x + 0,3(150 – x) = 42.
Решив уравнение, получим его единственный корень x = 60. Теперь ответим на вопрос задачи. Масса первого сплава 60 кг, масса второго сплава 90 кг, первая меньше второй на 30 кг.
Ответ. На 30 кг.
Задача 4. (2019) Первый сплав содержит 5 % меди, второй — 14 % меди. Масса второго сплава больше массы первого сплава на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.
Решение. Пусть масса первого сплава x кг, второго (x + 7) кг, третьего — (2x + 7) кг. Меди было в первом сплаве 0,05x кг, во втором — 0,14(x + 7) кг, в третьем — 0,1(2x + 7) кг. Составим уравнение:
0,05x + 0,14(x + 7) = 0,1(2x + 7).
Решив уравнение, получим его единственный корень x = 28. При x = 28 масса третьего сплава 2x + 7 равна 63 кг.
Ответ. 63 кг.
Задача 5. (2017) Смешав 70 %-й и 60 %-й растворы кислоты и добавив 2 кг чистой воды, получили 50 %-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90 %-го раствора той же кислоты, то получили бы 70 %-й раствор кислоты. Сколько килограммов 70 %-го раствора кислоты использовали для получения смеси?
Решение. Пусть масса первого раствора x кг, второго y кг. Приравняв массы кислоты до смешивания и после смешивания, составим два уравнения:
0,7x + 0,6y = 0,5(x + y + 2),
0,7x + 0,6y + 0,9*2 = 0,7(x + y + 2).
Решив систему этих двух уравнений, получим её единственное решение:
x = 3, y = 4. Использовали 3 кг 70 %-го раствора кислоты.
Ответ. 3 кг.
Задача 6. (2017) Имеется два сосуда. Первый содержит 100 кг, а второй — 50 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 28 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Для второго смешивания возьмём 1 кг первого раствора и 1 кг второго, получим 2 кг смеси. Составим первое уравнение:
Решив систему уравнений (1) и (2), получим её единственное решение: x = 12, y = 60. В первом сосуде содержится x * 100 / 100 = 12 (кг) кислоты. Ответ. 12 кг.
Для самостоятельного решения
7. Имеется 400 г морской воды, содержащей 4 % соли. Сколько граммов чистой воды нужно добавить в эту морскую воду, чтобы новый раствор содержал 2 % соли?
8. (2016) В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Определите процентную концентрацию того же вещества в новом растворе.
9. (2009) В бидон налили 4 литра молока трёхпроцентной жирности и 6 литров молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?
10. (2017) Имеется два сплава. Первый содержит 5 % никеля, второй — 20 % никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 15 % никеля. На сколько килограммов масса первого сплава меньше массы второго?
11. (2017) Первый сплав содержит 5 % меди, второй — 11 % меди. Масса второго сплава больше массы первого сплава на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.
12. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?
13. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?
Ответы. 7. 400 г. 8. 16 %. 9. 4,8 %. 10. На 75 кг. 11. 6 кг. 12. 5 : 2. 13. 5 : 2.
Для работы с задачами в классе можно использовать вариант заметки в виде презентации: Сплавы и смеси. Задачи 11 из ЕГЭ.
Источник
Другие методические материалы по теме
- Решение задач на взвешивание (определение фальшивой монеты)
Рассказываем, как в 4-5 классе решать задачи на переливание из одного сосуда в другой.
Задачи на переливание заключаются в том, что даётся два (иногда больше) сосудов разного объема, и путём манипуляций с наливанием воды в сосуды и переливанием из одного сосуда в другой надо добиться, чтобы в одном из сосудов оказался ровно заданный объём воды. Меток, указывающий объём, на сосудах нет, “на глазок” наливать нельзя.
Самый простой пример – пусть у нас есть два сосуда – 5 и 7 литров. Надо в один из сосудов налить ровно три литра воды.
Шаг 1. Наливаем в сосуд 5 л воды до краёв. Тем самым мы получаем 5 литров воды.
Шаг 2. Переливаем эту воду в сосуд 7 л. Теперь в нём 5 литров, а сосуд 5 литров пустой.
Шаг 3. Опять наливаем в сосуд 5 л. воду. В сосуде 7 л сейчас налито 5 л воды, значит есть ещё место для двух литров.
Шаг 4. Переливаем воду из сосуда 5 л в сосуд 7 л, пока он не наполнится до краёв. Те самым мы нальём в него ровно 2 л, т.к. в нём уже было 5 л, и оставалось ещё место для 2 л воды.
Раз мы из сосуда 5 л отлили 2 л, то в нём осталось 3 л. Задача решена.
Задача
Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов получить 1 л воды?
Изобразим решение на схеме. Прямоугольники означают сосуды, синий цвет – воду в сосудах. Под прямоугольниками – объём сосуда, над прямоугольником – объём воды в нём.
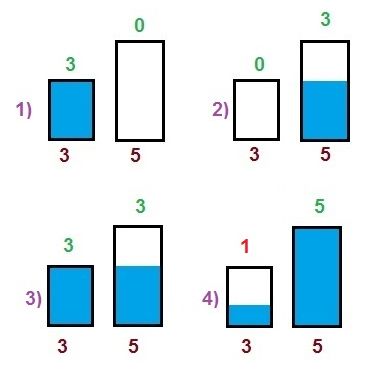
Пояснение к решению.
1 л воды можно получить, если из трёхлитрового сосуда отлить 2 литра воды. Значит нам надо добиться такой ситуации, когда в пятилитровом будем 3 литра воды, тем самым останется место ровно для двух литров, которые мы сможем перелить из трёхлитрового сосуда.
Шаг 1. Наливаем с трёхлитровый сосуд воду до краёв, получаем 3 литра воды
Шаг 2. Переливаем эту воду в пятилитровый сосуд. Теперь в нём 3 л воды, а в трёхлитровом пусто
Шаг 3. Опять наливаем в трёхлитровый сосуд воду, теперь по 3 л воды в каждом из сосудов.
Теперь мы добились той ситуации, которая нам была нужна – в пятилитровом сосуде есть место ровно для 2 л воды, а в трёхлитровом – 3 л воды.
Шаг 4. Переливаем воду из сосуда 3 л в сосуд 5 л, пока он не заполнится до краёв. Т.к. в нём было место для 2 л воды, то ровно эти 2 л и перельются, и в сосуде 3 л останется ровно 1 л. Залача решена.
Дата публикации
18.04.2020
Другие методические материалы по теме
- Решение задач на взвешивание (определение фальшивой монеты)
Купить наш видеокурс по подготовке к поступлению в 5-й класс физматшкол и участию в математических олимпиадах
Как готовиться к математическим олимпиадам и поступлению в физматшколу
Задачи раздела:
Более лёгкие задачи находятся внизу списка.
 | Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов налить 4 л воды? Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов налить 4 л воды? Подробно |
 | На столе стоят десять одинаковых банок, в каждой из них по 10 монет одного достоинства, в одной банке все монеты фальшивые На столе стоят десять одинаковых банок, в каждой из них по 10 монет одного достоинства. В одной из банок все монеты фальшивые. Настоящая монета весит 10 г, а фальшивая 9 г. У вас есть весы со шкалой в граммах. Как всего лишь за одно взвешивание определить, в какой из банок находятся фальшивые монеты? Подробно |
 | Сколько взвешиваний для определения фальшивой монеты надо, если монет от 28 до 81, и от 82 до 243 Имеется набор монет одинакового достоинства, одна из которых фальшивая. Подробно |
 | Решение задач на взвешивание (определение фальшивой монеты) Рассказываем, как в 4-5 классе решать задачи на определение фальшивой монеты за минимальное число взвешиваний. Подробно |
Источник
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 – x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 – x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 – x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 – x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 – x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 – x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
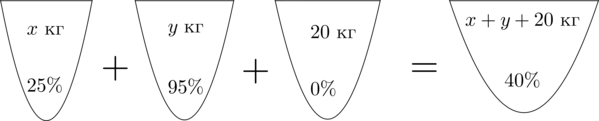
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
Аналогично составим схему, описывающую получение (50)-процентного раствора:
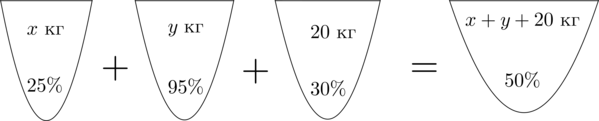
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20
Источник
