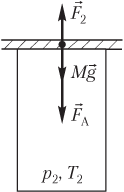Рисунок идеального газа в сосуде

5.4. Практическое применение уравнения состояния идеального газа

5.4.3. Уравнение состояния для газа, находящегося в сосуде под поршнем

Для идеального газа, находящегося в сосуде под поршнем, необходимо учитывать следующее:

• масса газа, находящегося в сосуде под поршнем, вследствие изменения термодинамических параметров газа не изменяется:

m = const;

• постоянным остается также количество вещества (газа):

ν = const;

• плотность газа и концентрация его молекул (атомов) изменяются:

ρ ≠ const, n ≠ const.

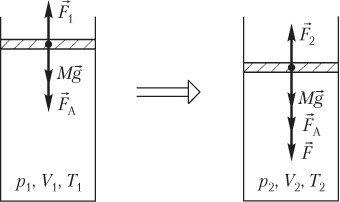
Пусть изменение состояния идеального газа, находящегося в цилиндрическом сосуде под поршнем, вызвано действием на поршень внешней силы F→ (рис. 5.9).

Рис. 5.9

Начальное и конечное состояния газа в сосуде под поршнем описываются следующими уравнениями:

p1V1=νRT1,p2V2=νRT2,}

где p
1, V
1, T
1 — давление, объем и температура газа в начальном состоянии; p
2, V
2, T
2 — давление, объем и температура газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).

Условия равновесия поршня, закрывающего идеальный газ в сосуде (см. рис. 5.9), в начале процесса и в конце процесса выглядят следующим образом:

Mg+FA=F1,Mg+FA+F=F2,}

где M — масса поршня; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; S — площадь сечения поршня; F
1 — модуль силы давления газа на поршень в начале процесса, F
1 = p
1S; p
1 — давление газа в сосуде в начальном состоянии; F — модуль силы, вызывающей сжатие газа; F
2 — модуль силы давления газа на поршень в конце процесса, F
2 = p
2S; p
2 — давление газа в сосуде в конечном состоянии.

Температура идеального газа, находящегося в сосуде под поршнем, может как изменяться, так и оставаться неизменной:

• если процесс движения поршня происходит достаточно быстро, то температура газа изменяется —

T ≠ const;

• если процесс происходит медленно, то температура газа остается постоянной –

T = const.

Давление идеального газа, находящегося в сосуде под поршнем, также может изменяться или оставаться неизменным:

• если в задаче сказано, что поршень является легкоподвижным, то давление газа под поршнем — неизменно (в том случае, когда из условия задачи не следует обратное) — p = const;
• в остальных случаях давление газа под поршнем изменяется — p ≠ const.

Масса поршня, закрывающего газ в сосуде, либо равна нулю, либо имеет отличное от нуля значение:

• если в задаче сказано, что поршень является легким или невесомым, то масса поршня считается равной нулю —

M = 0;

• в остальных случаях поршень обладает определенной ненулевой массой —

M ≠ const.

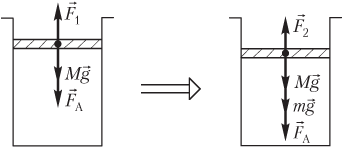
Пример 19. В вертикальном цилиндре под легкоподвижным поршнем сечением 250 мм2 и массой 1,80 кг находится 360 см3 газа. Атмосферное давление равно 100 кПа. На поршень поставили гири, и он сжал газ до объема 240 см3. Температура газа при его сжатии не изменяется. Определить массу гирь.

Решение. На рисунке показаны силы, действующие на поршень:

• сила тяжести поршня Mg→;
• сила атмосферного давления F→A;
• сила давления газа F→1, действующая со стороны газа (до его сжатия);
• сила давления газа F→2, действующая со стороны газа (после его сжатия);
• mg→ — вес гирь.

Условие равновесия поршня запишем в следующем виде:

• до сжатия газа —

F
1 = Mg + F
A,

где F
1 — модуль силы давления газа, F
1 = p
1S; p
1 — давление газа до сжатия; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление; g — модуль ускорения свободного падения;

• после сжатия газа —

F
2 = Mg + F
A
+ mg,

где F
2 — модуль силы давления газа, F
2 = p
2S; p
2 — давление газа после сжатия; mg — вес гирь; m — масса гирь.

Считая процесс сжатия газа изотермическим, запишем уравнение Менделеева — Клапейрона для газа под поршнем следующим образом:

• до его сжатия —

p
1V
1 = νRT,

где V
1 — первоначальный объем газа под поршнем; ν — количество газа под поршнем; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);

• после его сжатия —

p
2V
2 = νRT,

где V
2 — объем сжатого поршнем газа.

Равенство

p
1V
1 = p
2V
2

и два условия равновесия, записанные в явном виде, образуют полную систему уравнений:

p1S=Mg+pAS,p2S=Mg+pAS+mg,p1V1=p2V2,}

которую требуется решить относительно массы гирь m.

Для этого выразим отношение давлений p
2/p
1 из первой пары уравнений:

p2p1=Mg+pAS+mgMg+pAS

и из третьего уравнения:

p2p1=V1V2,

запишем равенство правых частей полученных отношений:

Mg+pAS+mgMg+pAS=V1V2.

Отсюда следует, что искомая масса определяется формулой

m=(M+pASg)(V1V2−1).

Вычисление дает результат:

m=(1,80+100⋅103⋅250⋅10−610)(360⋅10−6240⋅10−6−1)=2,15 кг.

Указанное сжатие газа вызвано гирями массой 2,15 кг.

Пример 20. Открытый цилиндрический сосуд сечением 10 см2 плотно прикрывают пластиной массой 1,2 кг. Атмосферное давление составляет 100 кПа, а температура окружающего воздуха равна 300 К. На сколько градусов нужно нагреть воздух в сосуде, чтобы он приподнял пластину?

Решение. На рисунке показаны силы, действующие на пластину после нагревания газа:

• сила тяжести пластины Mg→;
• сила атмосферного давления F→A;
• сила давления газа F→2, действующая на пластину со стороны нагретого газа.

Пластина находится в состоянии неустойчивого равновесия; условие равновесия пластины выглядит следующим образом:

F
2 = Mg + F
A,

где F
2 — модуль силы давления нагретого газа, F
2 = p
2S; p
2 — давление нагретого газа; S — площадь сечения сосуда; Mg — модуль силы тяжести пластины; M — масса пластины; g — модуль ускорения свободного падения; F
A — модуль силы атмосферного давления, F
A = p
AS; p
A — атмосферное давление.

Запишем уравнение Менделеева — Клапейрона следующим образом:

• для газа в сосуде до его нагревания

p
1V = νRT
1,

где p
1 — давление газа в сосуде до нагревания (совпадает с атмосферным давлением), p
1 = p
A; V — объем газа в сосуде; ν — количество вещества (газа) в сосуде; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в сосуде до нагревания (совпадает с температурой окружающей среды);

• для газа в сосуде после его нагревания

p
2V = νRT
2,

где p
2 — давление нагретого газа; T
2 — температура нагретого газа.

Два уравнения состояния газа (до и после нагревания) и условие равновесия пластины, записанные в явном виде, образуют полную систему уравнений:

pAV=νRT1,p2V=νRT2,p2S=Mg+pAS;}

систему необходимо решить относительно температуры T
2, до которой следует нагреть газ.

Для этого делением первой пары уравнений

pAVp2V=νRT1νRT2

получим выражение для давления нагретого газа:

p2=pAT2T1

и подставим его в третье уравнение системы:

pAT2ST1=Mg+pAS.

Преобразуем полученное выражение к виду

T2=T1(Mg+pAS)pAS=T1(MgpAS+1),

а затем найдем разность

ΔT=T2−T1=MgT1pAS.

Произведем вычисление:

ΔT=1,2⋅10⋅300100⋅103⋅10⋅10−4=36 К=36 °С.

Пример 21. В цилиндрическом сосуде поршень массой 75,0 кг и площадью сечения 50,0 см2 начинает двигаться вверх. Давление газа под поршнем постоянно и равно 450 кПа, атмосферное давление составляет 100 кПа. Считая, что поршень движется без трения, определить модуль скорости поршня после прохождения им 3,75 м пути.

Решение. На рисунке показаны силы, действующие на поршень:

• сила тяжести поршня Mg→;
• сила атмосферного давления F→A;
• сила давления газа F→, действующая на поршень со стороны нагретого газа.

Под действием указанных сил, направленных вверх, поршень движется с ускорением a→:

F→+F→A+Mg→=ma→,

или в проекции на вертикальную ось —

F − F
A − Mg = Ma,

где F — модуль силы давления газа под поршнем, F = pS; p — давление газа; S — площадь поршня; Mg — модуль силы тяжести поршня; M — масса поршня; g — модуль ускорения свободного падения; a — модуль ускорения поршня.

Преобразуем записанное уравнение, выразив модуль ускорения и выполнив подстановку выражений для модулей сил:

a=F−FA−MgM=(p−pA)SM−g.

Скорость поршня, его ускорение и пройденный путь связаны между собой соотношением

l=v22a,

где l — пройденный путь; v — модуль скорости поршня.

Выразим отсюда модуль скорости поршня:

v=2al

и подставим в записанную формулу выражение для модуля ускорения:

v=2l((p−pA)SM−g).

Выполним расчет:

v=2⋅3,75((450−100)⋅103⋅50⋅10−475,0−10)≈10 м/с.

После прохождения 3,75 м пути поршень приобретет скорость, приблизительно равную 10 м/с.