Рубашки сосудов и аппаратов
52857.8- 2007 |
2008 |
27 2002 . 184- , – 1.0-2004 .
1 – ( ); ( ); – – ( ); , ()
2 260
3 27 2007 . 503-
4 : 97/23 29 1997 . -, , ; 13445-3:2002 , . 3. (EN 13445-3:2002 Unfired pressure vessel – Part 3: De)
5
, – . () . , –
Vessels and apparatus. Norms and methods of strength calculation. Jacketed vessels and apparatus
– 2008-04-01
1
U- , , , , () , .
52857.1.
2
:
52857.1-2007 . .
52857.2-2007 . . ,
52857.6-2007 . .
– – , 1 , , . (), () . , , , , .
3
:
– ;
– , 2;
– , ;
– ;
b – , ;
b0 – , ;
b1 – , ;
b2 – , ;
– , ;
D1 – , ;
D2 – , ;
D3 – (D3 = D1 + s1), ;
D4 – (D4 = D2 + s2), ;
D – , ;
Dp – , : Dp = D1, Dp = D1;
d0 – , ;
d1 – , ; , d1 ;
1 – , ;
2 – , ;
0 – , ;
2 – , ;
F – , ;
F – , ;
f1, f2, f3, f4 – ;
f5, f6 – ;
G1 – , ;
G2 – , ;
– ;
h0 – , ;
h0 – , ;
h1 – , ;
h2 – [h2 = r3 (1 – cos γ)], ;
I – , , 4;
0, 1, 2 – ;
3, 4, 5, 6, 7, 8 – ;
9, 10, 11 – ;
L – , ;
l1, l2 – , ;
l3 – , , ; 52857.2;
l – , , ;
lR – , ;
0 – ;
M1, 2, 3 – ;
m – ;
N – ;
[N]i – Δσi 2.6.3 (i = 0; 1; 2;… 6);
1 – ;
2 – ;
3 – ;
– , ;
p1 – , . ( ), p1 > 0; (), p1 < 0;
2 – , ;
[2] – , ;
Q – ;
R1 – , ;
R2 – , ;
r0 – , ;
r1 – , ;
r2 – , ;
r3 – (r3 = r2 – 0,5s2), ;
s0 – , ;
sop – , ;
s1 – , ;
s1p – , ;
s2 – , ;
s2p – , ;
s3 – , ;
s4 – , ;
sp – , ; sp = s2, sp = s4;
T – , ;
ΔT1 – 20 ;
ΔT2 – 20 ;
t0 – , ;
t1, t2 – , ;
tp – ;
t – , :
tl – , ;
t – ;
ts – , ;
V – ;
W1 – , 2;
W2 – , 2;
1, 2, 3 – ;
α – ,… ;
α1 – , 1/;
α2 – , 1/;
β1, β2 – ;
γ – ;
γ – ,… ;
δT – ,…;
δD – ,…;
δ – ,…;
Δσi – (i = 0; 1; 2;… 6), ;
ε – ;
[ε] – ;
ε – ;
ε – , ;
η – ;
λ – ;
μ – ;
ρ – ;
σ – , ;
[σ]0 – , ;
[σ]1 – , ;
[σ]2 – , ;
[σ] – N, ;
[]i – (i = 0; 1; 2;…. 6), ;
φ0 – ;
φ1 – ;
φ2 – ;
φ3, φ4 – ;
φp1, φp2, φ3, φ4, φ5, φ6 – ;
φ0 – ;
φ1 – ;
φ2 – ;
φ1 – ;
φ2 – ;
χ – ;
ψ – ,… .
4
4.1
4.1.1 , (2 ≥ 0).
4.1.2 (. 5-8) , , , , 52857.1, ( ). , , :
380 – ;
420 – ;
525 – .
4.1.3 [] , , (r0, r1, r2), .
4.1.4 . , , 52857.6.
4.1.5 , . 15 , 52857.6.
4.2 U-
4.2.1 :
–
–
–
4.2.2 α = 30, α = 45
4.2.3 , N > 103 – (. .1, ).
4.2.4
h0 ≥ 1,5s2 – U- ,
– .
4.2.5 (. .2, ).
4.2.6.
d1 ≤ 0,4D2.
, .3, .
4.3 ,
4.3.1 δ
4.3.2 4.3-4.5
4.3.3 30 45 (. .4, ) .
4.3.4
a ≥ 0,7min{s0; s2}.
4.3.5 4.6
4.4
4.4.1 5 :
– b2 ≤ 0,1D1;
– h2 ≥ s2;
– 20 ≤ γ ≤ 90 .
4.4.2 V- , .
4.4.3 8.6
5 U-
5.1
5.1.1 52857.1. 2 – 1, 1 > 0.
5.1.2 52857.2. 1 < 0 |1|, 2 + |1|.
1 > 0 2 2 – 1, 1 2.
L 52857.2.
5.1.3 52857.2.
, :
) ts 0,3D1 n1 ≤ 1, ;
) l2 (. .5, ) , . , , l2 52857.2;
) b, l1, le 52857.2 :
b = max{ts – b1; l2 – 0,5b1}, (1)
(2)
(3)
) (. .6, ) ;
)
(4)
φ0 . s1, . .
5.2
5.2.1 52857.2. 5.1.1 5.1.2. , 2, , d1.
5.2.2 d1 .
5.3 (. .1, )
5.3.1 :
) :
(5)
) , :
(6)
) :
(7)
) :
(8)
) :
(9)
(1 < 0), (9) 1 = 0;
) :
(10)
(11)
)
(12)
5.3.2
(13)
5.3.3
(14)
(15)
(16)
(17)
f1, f2, f3 f4 .
f1:
–
–
f1 = λ + min (1; χ).
f2:
– α = 30
f2 = 1,22 (1 + 0,51ρ + 2εz),
– α = 45
f2 = 0,71 + 0,52ρ + εz,
f3:
– α = 30
– α = 45
f4:
– α = 30
– α = 45
5.3.4
. ,
:
(18)
s2 ≥ s2p + c. (19)
(5), B – (14), s2 .
5.4 (. .2, ).
5.4.1 :
)
(20)
(21)
)
(22)
(23)
(24)
)
(25)
)
(26)
1 > 2 > 0, (26) 1, 0;
)
(27)
)
3 = min {QH2; (1 + 2) 1}. (28)
5.4.2
(29)
5.4.3
(30)
h0 ≥ h0p + c. (31)
(30) . , 4.2.4.
5.4.4
(. .2,, , )
(32)
5.5
G1 G2
(33)
[2] – (13) (29) .
5.6
(34)
[p2] – (13) , (29) – .
5.6.1
(35)
ε, .
5.6.2 γ 1.
1 –
β1 | β2 | γ | ||
U- .5, | .1, | 4,0 | ||
.1, | – | – | ||
.1, | – | – | ||
.1, | – | – | , | |
.2, | 3,5 | |||
.2, | – | – | 3,5 | |
.2, | – | – | 3,0 | |
.2, | – | – | 5,5 | |
.6, | .1, | 2,5 | ||
.1, | 2,0 | 1,6 | 2,5 | |
.1, | 2,0 | |||
.1, | 2,0 | |||
.2, | 2,0 | 1,6 | 2,5 | |
.2, | 1,6 | 1,6 | 2,5 | |
.2, | 2,0 | 1,2 | 2,0 | |
.2, | 2,0 | 2,0 | 3,5 | |
, .8, | .4, | 2,0 | – | – |
.10, | 2,0 | – | – | |
.9, | .11, | 2,0 | – | – |
5.6.3
(36)
(37)
52857.6. [N]0 52857.6.
(38)
6 (. .7, )
6.1
5.1.1 – 5.1.3.
6.2 (. .1, )
, , , 4.2.2
(39)
6.3 (. .2, )
6.3.1 :
(40)
h0 ≥ max {s2; h0 + }. (41)
6.3.2
, .2, , , ,
(42)
– , .2, ,
= h0. (43)
6.4
(. 6.6.3), [2] (13) (29).
(44)
2
6.5
(45)
[p2] – (13) (29) .
(45) , .
6.6
6.6.1 (. .1, )
(46)
ε 5.6.1;
(47)
ε (6).
(48)
(49)
φ1 – 52857.2, .
(50)
β1, γ – . 1;
(51)
(52)
, .1, , , :
(53)
(54)
(55), – .1, , , – (56)
(55)
(56)
2.6.3. 1 , 2 .
6.6.2 (. .2, )
(57)
ε – . 5.6.3.
(58)
(59)
φ1 – 52857.2, ;
φ2 – 2.
2 –
(60)
(61)
(55) (56), 5.6.3. 1 , 2 .
6.6.3 6.6.1 6.6.2, , .
, Lε . 6.4.
6.6.4 , 52857.6.
7 , , (. .8, )
7.1
7.1.1 52857.2 1, 1 > 0.
7.1.2 1 < 0, 52857.2 |1|.
7.1.3 , , 2 7.4.3, .
1 < 0, (62) 7.3.1,
(62)
7.2
7.2.1 52857.2 1 1 > 0, |1|, 1 < 0.
7.2.2 , , 2 7.3, . s1 s3 s2 s4.
7.3
7.3.1
– :
(63)
– :
(64)
f5 f6 d0/t0 , (66),
(65)
(66)
7.3.2
:
(67)
(68)
(69)
d0/t0 m f5 f6. d0, t1 t2 . tp t (69) (65) 4.3.2.
:
(70)
s1 ≥ s1p + c, (71)
(72)
s2 ≥ s2p + c. (73)
s2 s2 .
7.3.3 ,
6.2 – 6.3.
:
(74)
(75)
f6 (66).
7.4 (. .4, )
(76)
s2 = a ≥ s2p + c, (77)
(78)
t0 (65).
7.5 (. .4, )
(79)
η (78).
s0 ≥ s0p + . (80)
:
a ≥ 1,41s0p + c. (81)
(80) (81) 4.3.4.
7.6
7.6.1 :
)
(82)
)
(83)
– :
(84)
(85)
– :
(86)
(87)
– :
7.6.2
(88)
(89)
7.6.3 :
(90)
(91)
5.6.3. 3 , 4 .
7.7 , 7, , .
8
8.1
8.1.1 52857.2 1, 1 > 0.
8.1.2 1 > 0, 52857.2 |1|.
8.1.3 ( .9, ) , 52857.2, , :
) ts 0,3D1. 2 ≤ 3 + 1, , ;
) l2 52857.2 , (. .9, ) , ;
) b, l1 l 52857.2 :
(92)
(93)
(94)
) 52857.2 , I A :
(95)
(96)
(97)
8.1.4 2 , b2 8.3.
8.2
8.2.1 52857.2 1 1 > 0, 1 1 < 0.
8.2.2 2 , b2 8.3.2.
8.3
8.3.1 :
(98)
1 < 0, :
(99)
2 > 1 > 0, :
(100)
8.3.2
(101)
8.4
8.4.1
V 52857.3. , V
(102)
:
– V- (. .9, , ):
φ5 = φ6 = φ2. (103)
– (. .9, ):
(104)
φ6 = 0,4. (105)
φ3 φ4 :
φ3 = min {V; φ5}; (106)
φ4 = min {V; φ6}. (107)
8.4.2
(108)
8.4.3 :
(109)
s2 ≥ s2p + c, (110)
a ≥ 0,6s2p. (111)
8.5 (. .9, ).
8.4, V, φ3, φ4 :
(112)
φ3 = Vφp5, (113)
φ4 = Vφp6. (114)
8.6
8.6.1
(115)
(116)
(117)
(118)
8.6.2
(119)
8.6.3 :
(120)
(121)
5.6.3. 5 , 6 – .
()
,
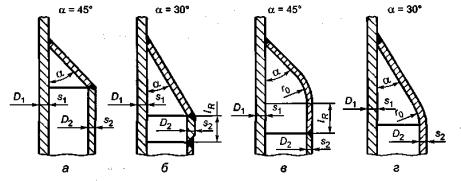
.1 –
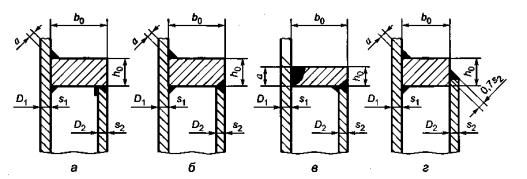
.2 –
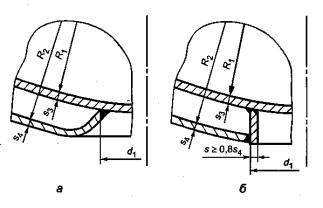
– –
.3 –
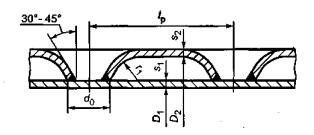
.4 –
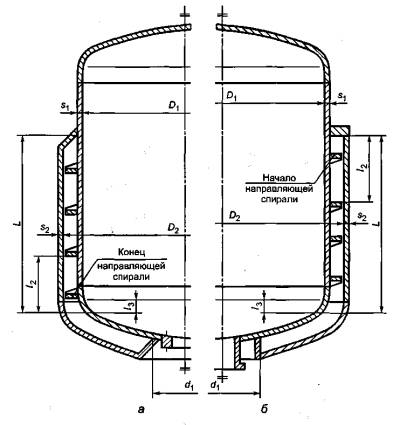
– ; –
.5 – U-
.6 –
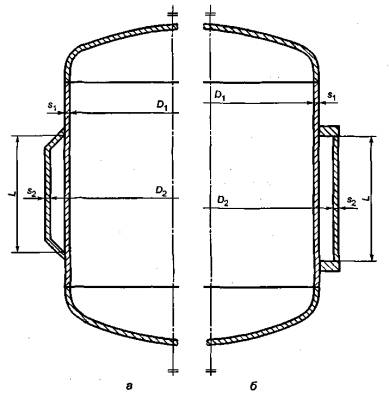
– ; –
.7 –
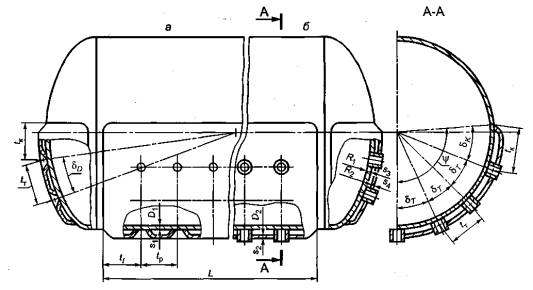
– ; –
.8 – ,
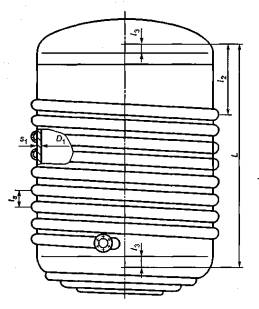
.9 –
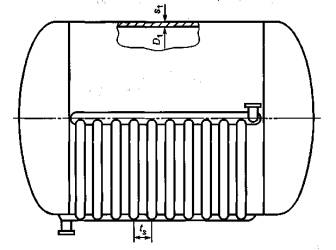
.9 –
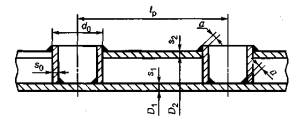
.10 –
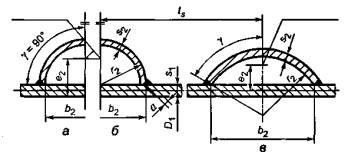
– V- ; – ; –
.11 –
: ,
Источник
|
Источник
27 2002 . 184- , – 1.0-2004 . 1 – ( ); ( ); – – ( ); , () 2 260 3 27 2007 . 503- 4 : 97/23 29 1997 . -, , ; 13445-3:2002 , . 3. (EN 13445-3:2002 Unfired pressure vessel – Part 3: De) 5 , – . () . , – Vessels and apparatus. Norms and methods of strength calculation. Jacketed vessels and apparatus – 2008-04-01 U- , , , , () , . 52857.1. : 52857.1-2007 . . 52857.2-2007 . . , 52857.6-2007 . . – – , 1 , , . (), () . , , , , . : – ; – , 2; – , ; – ; b- , ; b0- , ; b1- , ; b2- , ; – , ; D1- , ; D2- , ; D3- (D3= D1+ s1), ; D4- (D4= D2+ s2), ; D- , ; Dp – , : Dp= D1, Dp = D1; d0- , ; d1- , ; , d1 ; 1- , ; 2- , ; 0- , ; 2- , ; F – , ; F- , ; f1, f2, f3, f4- ; f5, f6- ; G1- , ; G2- , ; – ; h0- , ; h0- , ; h1- , ; h2- [h2= r3(1 – cosγ)], ; I- , , 4; 0, 1, 2 – ; 3, 4, 5, 6, 7, 8 – ; 9, 10, 11 – ; L – , ; l1, l2- , ; l3- , , ; 52857.2; l- , , ; lR- , ; 0- ; M1, 2, 3 – ; m- ; N- ; [N]i – Δσi 2.6.3 (i= 0; 1; 2;… 6); 1- ; 2- ; 3- ; – , ; p1- , . ( ), p1> 0; (), p1< 0; 2- , ; [2] – , ; Q – ; R1- , ; R2- , ; r0- , ; r1- , ; r2- , ; r3- (r3= r2- 0,5s2), ; s0- , ; sop – , ; s1 – , ; s1p – , ; s2- , ; s2p – , ; s3- , ; s4- , ; sp – , ; sp = s2, sp = s4; T – , ; ΔT1- 20 ; ΔT2- 20 ; t0- , ; t1, t2- , ; tp – ; t- , : tl- , ; t- ; ts – , ; V – ; W1- , 2; W2- , 2; 1, 2, 3 – ; α – ,… ; α1 – , 1/; α2 – , 1/; β1, β2 – ; γ – ; γ – ,… ; δT – ,…; δD – ,…; δ – ,…; Δσi – (i= 0; 1; 2;… 6), ; ε – ; [ε] – ; ε – ; ε – , ; η – ; λ – ; μ – ; ρ – ; σ – , ; [σ]0 – , ; [σ]1 – , ; [σ]2 – , ; [σ] – N, ; []i- (i = 0; 1; 2;…. 6), ; φ0 – ; φ1 – ; φ2 – ; φ3, φ4 – ; φp1, φp2, φ3, φ4, φ5, φ6 – ; φ0 – ; φ1 – ; φ2 – ; φ1 – ; φ2 – ; χ – ; ψ – ,… . 4.1 4.1.1 , (2 ≥ 0). 4.1.2 (. 5-8) , , , , 52857.1, ( ). , , : 380 – ; 420 – ; 525 – . 4.1.3 [] , , (r0, r1, r2), . 4.1.4 . , , 52857.6. 4.1.5 , . 15 , 52857.6. 4.2 U- 4.2.1 : – – – 4.2.2 α = 30, α = 45 4.2.3 , N > 103 – (. .1, ). 4.2.4 h0≥ 1,5s2 – U- , – . 4.2.5 (. .2, ). 4.2.6. d1≤ 0,4D2. , .3, . 4.3 , 4.3.1 δ 4.3.2 4.3-4.5 4.3.3 30 45 (. .4, ) . 4.3.4 a ≥ 0,7min{s0; s2}. 4.3.5 4.6 4.4 4.4.1 5 : – b2 ≤ 0,1D1; – h2 ≥ s2; – 20 ≤ γ ≤ 90 . 4.4.2 V- , . 4.4.3 8.6 5.1 5.1.1 52857.1. 2 – 1, 1 > 0. 5.1.2 52857.2. 1 < 0 |1|, 2 + |1|. 1 > 0 2 2 – 1, 1 2. L 52857.2. 5.1.3 52857.2. , : ) ts 0,3D1 n1≤ 1, ; ) l2 (. .5, ) , . , , l2 52857.2; ) b, l1, le 52857.2 : b = max{ts – b1; l2 – 0,5b1}, (1) (2) (3) ) (. .6, ) ; ) (4) φ0 . s1, . . 5.2 5.2.1 52857.2. 5.1.1 5.1.2. , 2, , d1. 5.2.2 d1 . 5.3 (. .1, ) 5.3.1 : ) : (5) ) , : (6) ) : (7) ) : (8) ) : (9) (1 < 0), (9) 1 = 0; ) : (10) (11) ) (12) 5.3.2 (13) 5.3.3 (14) (15) (16) (17) f1, f2, f3 f4 . f1: – – f1= λ + min(1; χ). f2: – α = 30 f2= 1,22 (1 + 0,51ρ + 2εz), – α = 45 f2= 0,71 + 0,52ρ+ εz, f3: – α = 30 – α = 45 f4: – α = 30 – α = 45 5.3.4 . , : (18) s2 ≥ s2p + c. (19) (5), B – (14), s2 . 5.4 (. .2, ). 5.4.1 : ) (20) (21) ) (22) (23) (24) ) (25) ) (26) 1 > 2 > 0, (26) 1, 0; ) (27) ) 3= min {QH2; (1 + 2) 1}. (28) 5.4.2 (29) 5.4.3 (30) h0≥ h0p + c. (31) (30) . , 4.2.4. 5.4.4 (. .2,, , ) (32) 5.5 G1 G2 (33) [2] – (13) (29) . 5.6 (34) [p2] – (13) , (29) – . 5.6.1 (35) ε, . 5.6.2 γ 1. 1 –
5.6.3 (36) (37) 52857.6. [N]0 52857.6. (38) 6.1 5.1.1 – 5.1.3. 6.2 (. .1, ) , , , 4.2.2 (39) 6.3 (. .2, ) 6.3.1 : (40) h0≥ max{s2; h0+ }. (41) 6.3.2 , .2, , , , (42) – , .2, , = h0. (43) 6.4 (. 6.6.3), [2] (13) (29). (44) 2 6.5 (45) [p2] – (13) (29) . (45) , . 6.6 6.6.1 (. .1, ) (46) ε 5.6.1; (47) ε (6). (48) (49) φ1- 52857.2, . (50) β1, γ – . 1; (51) (52) , .1, , , : (53) (54) (55), – .1, , , – (56) (55) (56) 2.6.3. 1 , 2 . 6.6.2 (. .2, ) (57) ε – . 5.6.3. (58) (59) φ1 – 52857.2, ; φ2 – 2. 2 – (60) (61) (55) (56), 5.6.3. 1 , 2 . 6.6.3 6.6.1 6.6.2, , . , Lε . 6.4. 6.6.4 , 52857.6. 7.1 7.1.1 52857.2 1, 1 > 0. 7.1.2 1 < 0, 52857.2 |1|. 7.1.3 , , 2 7.4.3, . 1 < 0, (62) 7.3.1, (62) 7.2 7.2.1 52857.2 1 1 > 0, |1|, 1 < 0. 7.2.2 , , 2 7.3, . s1 s3 s2 s4. 7.3 7.3.1 – : (63) – : (64) f5 f6 d0/t0 , (66), (65) (66) 7.3.2 : (67) (68) (69) d0/t0 m f5 f6. d0, t1 t2 . tp t (69) (65) 4.3.2. : (70) s1≥ s1p + c, (71) (72) s2≥ s2p + c. (73) s2 s2 . 7.3.3 , 6.2 – 6.3. : (74) (75) f6 (66). 7.4 (. .4, ) (76) s2 = a ≥ s2p + c, (77) (78) t0 (65). 7.5 (. .4, ) (79) η (78). s0≥ s0p + . (80) : a ≥ 1,41s0p + c. (81) (80) (81) 4.3.4. 7.6 7.6.1 : ) (82) ) (83) – : (84) (85) – : (86) (87) – : 7.6.2 (88) (89) 7.6.3 : (90) (91) 5.6.3. 3 , 4 . 7.7 , 7, , . 8.1 8.1.1 52857.2 1, 1 > 0. 8.1.2 1 > 0, 52857.2 |1|. 8.1.3 ( .9, ) , 52857.2, , : ) ts 0,3D1. 2 ≤ 3 + 1, , ; ) l2 52857.2 , (. .9, ) , ; ) b, l1 l 52857.2 : (92) (93) (94) ) 52857.2 , I A : (95) (96) (97) 8.1.4 2 , b2 8.3. 8.2 8.2.1 52857.2 1 1 > 0, 1 1 < 0. 8.2.2 2 , b2 8.3.2. 8.3 8.3.1 : (98) 1 < 0, : (99) 2 > 1 > 0, : (100) 8.3.2 (101) 8.4 8.4.1 V 52857.3. , V (102) : – V- (. .9, , ): φ5 = φ6 = φ2. (103) – (. .9, ): (104) φ6 = 0,4. (105) φ3 φ4 : φ3 = min {V; φ5}; (106) φ4 = min {V; φ6}. (107) 8.4.2 (108) 8.4.3 : (109) s2≥ s2p + c, (110) a≥ 0,6s2p. (111) 8.5 (. .9, ). 8.4, V, φ3, φ4 : (112) φ3 = Vφp5, (113) φ4 = Vφp6. (114) 8.6 8.6.1 (115) (116) (117) (118) 8.6.2 (119) 8.6.3 : (120) (121) 5.6.3. 5 , 6 – .
.1 –
.2 –
– – .3 –
.4 –
– ; – .5 – U- .6 –
– ; – .7 –
– ; – .8 – ,
.9 –
.9 –
.10 –
– V- ; – ; – .11 – : , |
Источник






















