Сила архимеда давление в сосудах
С. Н. Манида
Установлена зависимость силы гидростатического давления (силы Архимеда) от плотности свободного тела, погруженного в жидкость.
1. Закон Архимеда для неподвижных тел
Любое тело, погруженное в жидкость, подвергается сжимающему и выталкивающему действию со стороны жидкости.
Представим такую ситуацию: ученый, владеющий современными приборами и мощным математическим аппаратом, решил вычислить силу, выталкивающую из жидкости погруженное в нее тело.
Он экспериментально установит, что на единицу поверхности тела, погруженного в жидкость с плотностью действует по нормали к поверхности сила гидростатического давления p, зависящая от глубины погружения h по определенному закону (gh) и не зависящая от ориентации поверхности.
Он сложит векторы сил давления, действующих на различные элементы поверхности тела и направленные по нормали к ним; для этого потребуется вычислить так называемый поверхностный интеграл от некоторой векторной функции по поверхности тела сложной формы. С помощью современного математического аппарата и мощных компьютеров этот интеграл может быть вычислен. Но каково же будет изумление этого ученого, когда окажется, что полученный результат численно равен весу жидкост и в объеме погруженной части тела! Этот результат был получен греческим ученым Архимедом 2200 лет назад, причем в общем виде — для тел любой формы!
Попробуем восстановить ход рассуждений Архимеда и вывести его закон.
На рис. 1, изображено тело, помещенное в жидкость. На это тело со стороны жидкости действует описанная выше сила гидростатического давления. Для нахождения этой силы вместо вычисления сложных интегралов проведем мысленный эксперимент: уберем тело и рассмотрим жидкость в объеме V, который занимала погруженная часть тела (рис. 2). На эту жидкость действует сила тяжести Vg и сила гидростатического давления F. Выделенный объем находится в равновесии, следовательно, сумма сил, действующих на жидкость в этом объеме, равна нулю: F+ Vg =0.
Отсюда следует выражение для силы гидростатического давления: F=-Vg.
Мы нашли силу, действующую на поверхность жидкости, заполняющей объем V. Но поверхность тела, погруженного в жидкость, совпадает с поверхностью жидкости в нашем мысленном эксперименте, следовательно, найденное выражение и есть «выталкивающая’’ сила — сила Архимеда
F Арх = -Vg. (*)
Это равенство и носит название закон Архимеда.
2. Неприменимость закона Архимеда для случая свободных тел
Казалось бы, решение задач с использованием этого закона не должно вызывать затруднений. Однако неверные решения отдельных задач на закон Архимеда встречаются не только у школьников, но и в ряде задачников.
Дело в том, что при использовании этого (как и любого другого) закона надо всегда помнить, как и для каких ситуаций он выводился. Так, например, мы вычисляли силу гидростатического давления, действующую на поверхность неподвижного объема жидко сти, находящейся в равновесии, т. е. имеющей нулевые скорость и ускорение. Следовательно, и использовать выведенное выражение для силы Архимеда можно только в тех случаях, когда и скорость, и ускорение тела равны нулю.
Покажем, что применение этого закона в других ситуациях абсолютно неправомочно, так как приводит к неверным результатам.
Рассмотрим легкое тело, привязанное ниткой к дну сосуда, заполненного жидкостью (рис. 3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg= Vg и сила натяжения нити T, а вверх — сила гидростатического давления
F=FАрх=- Vg, (*)
где – плотность тела, – плотность жидкости. Условие равновесия тела
-Vg +T+Vg =0. (1)
Пусть в некоторый момент нить обрывается (т. е. исчезает сила натяжения T), равенство (1) перестает выполняться, и тело начинает двигаться вве рх (всплывать) с некоторым ускорением a, которое можно найти из уравнения движения
F+ V g = V a. (2)
Предположив, что в этом случае можно использовать закон Архимеда, подставим – Vg в левую часть равенства (2) вместо F. Для ускорения тела получаем выражение
a = — g (-)/ (3)
Исследуем выражение (3). Ускорение тела направлено против ускорения свободного падения (что абсолютно верно), а его величина неограниченно возрастает при уменьшении плотности тела. Такой результат противоречит как здравому смыслу, так и наблюдениям.
Таким образом, закон Архимеда в форме (*) неприменим к телам, ускорение которых относительно жидкости отлично от нуля (даже при равной нулю скорости).
3. Сила гидростатического давления для случая свободных тел
Точный расчет гидростатического давления на поверхность ускоренно движущегося тела возможен только с применением аппарата математической физики, а ответ представим в аналитическом виде лишь для некоторых частных случаев. Уравнения, описывающие движение тела в жидкости, были впервые получены профессором Петербургского университета Леонардом Эйлером в середине XVIII века. Решение этой задачи для случая тела сферической формы, размеры которого много меньше размеро в сосуда, приведено в Приложении (для читателей, владеющих методами постановки и решения граничных задач математической физики). Полученное там выражение (**) для силы давления отличается от (*):
(4)
и, с учетом (2), ускорение тела имеет вид:
(5)
4. Выводы
Сравнивая выражения (4) и (*) видим, что они совпадают только при = . Зависимость силы гидростатического давления, действующей на свободное тело, от его плотности представлена на графике рис. 4 в сравнении со стандартным выражением для силы Архимеда Vg:
Из графика на рис.4 видно, что для малых плотностей тела сила давления убывает до нуля, а при увеличении плотности эта сила стремится к величине 1,5Vg.
На следующем графике (рис. 5) приведена зависимость ускорения свободного тела в жидкости от его плотности [уравнение (5)]. Для сравнения приведен график ускорения, получающийся непосредственн о из закона Архимеда [уравнение (3)]
Из этого графика видно, что даже бесконечно легкий шарик всплывает с конечным ускорением, равным -2g, а тяжелые тела тонут с ускорением, меньшим, чем это следует из закона Архимеда.
Источник
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Закон Архимеда
На погружённое в жидкость или газ тело действует выталкивающая сила, и равная весу среды, объём которой равен объёму тела.
Выталкивающая сила (сила Архимеда) равна
[F_A=rho_text{ж} g V_text{пчт}] где (displaystyle V_text{пчт}) — объём погружённой части тела, (displaystyle rho_text{ж}) — плотность жидкости.
Плавание тел
Рассмотрим тело плотности (rho) и жидкость плотности (rho_0). Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести (mg) и архимедова сила (F_A). Если объём тела равен V, то
[mg=rho g V,] [F_A=rho_0 g V]
Имеются три возможности дальнейшего движения тела.
Сила тяжести больше архимедовой силы: (displaystyle mg > F_A), или (displaystyle rho>rho_0). В этом случае тело тонет.
Сила тяжести равна архимедовой силе: (displaystyle mg = F_A), или (displaystyle rho=rho_0). В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
Сила тяжести меньше архимедовой силы: (displaystyle mg < F_A), или (displaystyle rho<rho_0). В этом случае тело всплывает, достигая поверхности жидкости.
Таким образом, условие плавания тела можно записать в виде неравенства (displaystyle rholeq rho_0).
Два жестко связанные друг с другом одинаковых бруска, имеющие толщину (h=5) см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.)
Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
(displaystylerho_1) – плотность материала, из которого изготовлены бруски, а (displaystyle V) – объем двух брусков. Тогда масса этих брусков будет равна [displaystyle m=rho_1V] Сила, с которой льдинки действуют на воду, равна силе тяжести [displaystyle F=mg=rho_1Vg] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда [F_text{Арх}=rho gfrac{V}2,] где (displaystyle rho) – плотность воды, (displaystyle frac{V}2) – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: [rho_1Vg=rho gfrac{V}2,] откуда (displaystyle rho_1=dfrac{rho}2,) то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину [frac72h=3,5cdot5text{ см}=17,5 text{ см}.] Глубина увеличится на (displaystyle 17,5 -5=12,5) см.
Ответ: 12,5
Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна (displaystyle rho_text{ ал}=2700 text{ кг}/text{м}^3. ) Какова длина ребра куба, если выталкивающая сила равна (displaystyle F_text{Арх}=33,75text{ Н}?) (Ответ дайте в сантиметрах.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV,] где (displaystyle rho_text{в}) – плотность жидкости, в которую погружен кубик, (displaystyle V) – объем погруженной части тела. Так как куб погружен целиком, то (displaystyle V=a^3), получим: [F_text{Арх}=rho_text{в} ga^3] Выразив из этой формулы сторону (displaystyle a), получаем [a=sqrt[3]{frac{F_text{Арх}}{rho_text{в}g }}] Подставив значения в формулу, получим: [a=sqrt[3]{frac{33,75text{ Н}}{10text{ м}/{c^2}cdot1000text{ кг}/text{м}^3}}=0,15text{ м}=15text{ cм }]
Ответ: 15
Однородный цилиндр, изготовленный из материала плотностью (displaystyle rho=600) кг/м(^3), с радиусом основания (displaystyle R=25) см и высотой (displaystyle H=20) см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)

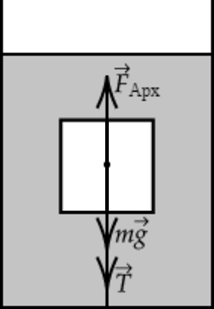
Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: [vec T+vec F_text{Арх}+mvec g=mvec a,] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [T- F_text{Арх}+mg=0, quad(1)] массу цилиндра можно рассчитать, исходя из формулы (displaystyle rho=frac {m}{V} Rightarrow m=rho V,) где V – объем цилиндра, который можно вычислить по формуле [V=pi R^2 H] Из формулы (1) выразим силу натяжения нити T:[T=F_text{Арх}-mg=rho_text{в}gV-rho gV=Vg(rho_text{в}-rho)=pi R^2 Hg(rho_text{в}-rho),] где (displaystyle rho_text{в}) – плотность воды, подставим в получившееся выражение численные значения:[T=3,14cdot0,25^2text{ м}cdot0,2text{ м}cdot 10text{ м}/text{с}^2 cdot (1000text{ кг}/text{м}^3-600text{ кг}/text{м}^3)=157text{ Н }]
Ответ: 157
Однородный кубический предмет с ребром (displaystyle a=18) см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна (displaystyle rho_text{др}=340) кг/м(^3), плотность эфира (displaystyle rho_text{э}=720) кг/м(^3). (Ответ дайте в сантиметрах.)
Запишем условие равновесия кубика на поверхности эфира: [F_text{ Арх}=mg, quad(1)] где (F_text{ Арх}) – выталкивающая сила, действующая на брусок, (displaystyle m) – масса кубика, которую можно рассчитать, исходя из формулы (displaystyle rho_text{др}=frac {m}{V} Rightarrow m=rho_text{др} V,) где V – объем кубика, который можно вычислить по формуле [V=a^3.] Выталкивающая сила равна: [F_text{ Арх}=rho_text{э}gV_text{пчт},] где (displaystyle V_text{пчт}) – объем погруженной части кубика,[V_text{пчт}=xa^2,] где (displaystyle x) – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: [rho_text{э}gxa^2=rho_text{др}a^3] [rho_text{э}x=rho_text{др}a, text{ выразим } x=frac{rho_text{др}a}{rho_text{э}}.] Пусть (displaystyle y) – длина части стороны, находящейся над эфиром, можем записать: [y=a-x,] искомая разница длин (displaystyle delta=y-x=a-2x=a-2cdot dfrac{rho_text{др}a}{rho_text{э}}=a(1-2cdot dfrac{rho_text{др}}{rho_text{э}})) подставим в получившееся выражение численные значения: [displaystyle delta=0,18text{ м}(1-2cdot dfrac{340text{ кг}/text{м}^3}{720text{ кг}/text{м}^3})=0,01text{ м}=1text{ см}]
Ответ: 1
В некий резервуар было налито 1000 литров жидкости плотностью (displaystyle rho_1=1500) кг/м(^3). В этой жидкости в равновесии плавает кубик, погруженный в воду на (displaystyle x=130) см. Длина стороны кубика равна (displaystyle a=200) см. В сосуд доливают ещё 1000 литров жидкости плотностью (displaystyle rho_2=1100) кг/м(^3) и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)
В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. [rho_text{нов}=dfrac{rho_1+rho_2}{2}] Так как кубик плавает на поверхности, то можно записать: [mg=F_text{Арх},] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна:[F_text{Арх1}=rho_1 g V_text{пчт1},] где (displaystyle V_text{пчт1}=a^2x) – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: [F_text{Арх2}=rho_text{нов} g V_text{пчт2}=dfrac{rho_1+rho_2}{2}g V_text{пчт2},]где (displaystyle V_text{пчт2}=a^2y) – объем погруженной части куба до смешивания, (displaystyle y) – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим [rho_1 g a^2x=dfrac{rho_1+rho_2}{2} g a^2y] [rho_1x=dfrac{rho_1+rho_2}{2}y,] выразим отсюда y: [y=frac{2rho_1 x}{rho_1+rho_2},] подставим в получившееся выражение численные значения: [y=frac{2cdot1500text{ кг}/text{м}^3 cdot1,3text{ м}}{1500text{ кг}/text{м}^3+1100text{ кг}/text{м}^3}=1,5text{ м}]
Ответ: 1,5
Стеклянный шарик опускается в воде с ускорением (displaystyle a=6) м/с(^2). Найти плотность стекла. Плотность воды (displaystyle rho_text{в}=1000) кг/м(^3). Силами вязкого трения пренебречь. (Ответ дайте в кг/м(^3).)
При движении шарика в воде на него действует сила тяжести (displaystyle mvec g) и сила Архимеда (displaystyle F_text{Арх}). Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: [vec F_text{Арх}+mvec g=mvec a,] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [mg- F_text{Арх}=ma,] Отсюда с учетом выражения для силы Архимеда (displaystyle F_text{Арх}=rho_text{в} g V), где V – объем шарика, а
(displaystyle rho_text{в}) – плотность воды, получим: [mg- rho_text{в} g V=ma,] Выразим массу шарика:[m=frac{rho_text{в} g V}{g-a}.] Исходя из формулы, плотность стекла равна [displaystyle rho_text{ст}=frac {m}{V}=frac{rho_text{в} g V}{(g-a)V}=frac{rho_text{в} g }{g-a},] подставим в получившееся выражение численные значения: [rho_text{ст}=frac{1000 text{ кг}/text{м}^3cdot 10text{ м}/text{с}^2 }{10text{ м}/text{с}^2-6text{ м}/text{с}^2}=2500text{ кг}/text{м}^3]
Ответ: 2500
Однородный шарик, изготовленный из материала плотностью (displaystyle rho=2000) кг/м(^3) погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
(displaystyle F_text{Арх}=100) Н? (Ответ дайте в сантиметрах и округлите до целых.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV_text{пчт},] где (displaystyle rho_text{в}) – плотность воды, (displaystyle V_text{пчт}) – объем погруженной части тела. Так как шар полностью опущен в воду, то [V_text{пчт}=frac43pi R^3,] где (displaystyle R) – радиус шара, получим: [F_text{Арх}=rho_text{в} gfrac43pi R^3, (1)] выразим из формулы R: [R=sqrt[3]{frac{3F_text{Арх}}{4rho_text{в}gpi}}] Подставив значения в формулу, получим: [R=sqrt[3]{frac{3 cdot100text{ Н}} {4 cdot1000 text{ кг}/text{м}^3cdot10text{ м}/{c^2}cdot3,14}} approx0,13text{ м}=13text{ см }]
Ответ: 13
Источник
Çàêîí Àðõèìåäà — çàêîí ñòàòèêè æèäêîñòåé è ãàçîâ, ñîãëàñíî êîòîðîìó íà âñÿêîå òåëî, ïîãðóæåííîå â æèäêîñòü (èëè ãàç), äåéñòâóåò ñî ñòîðîíû ýòîé æèäêîñòè (èëè ãàçà) âûòàëêèâàþùàÿ ñèëà, ðàâíàÿ âåñó âûòåñíåííîé òåëîì æèäêîñòè (ãàçà) è íàïðàâëåííàÿ ïî âåðòèêàëè ââåðõ.
Ýòîò çàêîí áûë îòêðûò äðåâíåãðå÷åñêèì ó÷åíûì Àðõèìåäîì â III â. äî í. ý. Ñâîè èññëåäîâàíèÿ Àðõèìåä îïèñàë â òðàêòàòå «Î ïëàâàþùèõ òåëàõ», êîòîðûé ñ÷èòàåòñÿ îäíèì èç ïîñëåäíèõ åãî íàó÷íûõ òðóäîâ.
Íèæå ïðèâåäåíû âûâîäû, ñëåäóþùèå èç çàêîíà Àðõèìåäà.
Äåéñòâèå æèäêîñòè è ãàçà íà ïîãðóæåííîå â íèõ òåëî .
Åñëè ïîãðóçèòü â âîäó ìÿ÷èê, íàïîëíåííûé âîçäóõîì, è îòïóñòèòü åãî, òî îí âñïëûâåò. Òî æå ñàìîå ïðîèçîéäåò ñî ùåïêîé, ñ ïðîáêîé è ìíîãèìè äðóãèìè òåëàìè. Êàêàÿ æå ñèëà çàñòàâëÿåò èõ âñïëûâàòü?
Íà òåëî, ïîãðóæåííîå â âîäó, ñî âñåõ ñòîðîí äåéñòâóþò ñèëû äàâëåíèÿ âîäû (ðèñ. à).  êàæäîé òî÷êå òåëà ýòè ñèëû íàïðàâëåíû ïåðïåíäèêóëÿðíî åãî ïîâåðõíîñòè. Åñëè áû âñå ýòè ñèëû áûëè îäèíàêîâû, òåëî èñïûòûâàëî áû ëèøü âñåñòîðîííåå ñæàòèå. Íî íà ðàçíûõ ãëóáèíàõ ãèäðîñòàòè÷åñêîå äàâëåíèå ðàçëè÷íî: îíî âîçðàñòàåò ñ óâåëè÷åíèåì ãëóáèíû. Ïîýòîìó ñèëû äàâëåíèÿ, ïðèëîæåííûå ê íèæíèì ó÷àñòêàì òåëà, îêàçûâàþòñÿ áîëüøå ñèë äàâëåíèÿ, äåéñòâóþùèõ èà òåëî ñâåðõó.
Åñëè çàìåíèòü âñå ñèëû äàâëåíèÿ, ïðèëîæåííûå ê ïîãðóæåííîìó â âîäó òåëó, îäíîé (ðåçóëüòèðóþùåé èëè ðàâíîäåéñòâóþùåé) ñèëîé, îêàçûâàþùåé íà òåëî òî æå ñàìîå äåéñòâèå, ÷òî è âñå ýòè îòäåëüíûå ñèëû âìåñòå, òî ðåçóëüòèðóþùàÿ ñèëà áóäåò íàïðàâëåíà ââåðõ. Ýòî è çàñòàâëÿåò òåëî âñïëûâàòü. Ýòà ñèëà íàçûâàåòñÿ âûòàëêèâàþùåé ñèëîé, èëè àðõèìåäîâîé ñèëîé (ïî èìåíè Àðõèìåäà, êîòîðûé âïåðâûå óêàçàë íà åå ñóùåñòâîâàíèå è óñòàíîâèë, îò ÷åãî îíà çàâèñèò). Íà ðèñóíêå á îíà îáîçíà÷åíà êàê FA.

Àðõèìåäîâà (âûòàëêèâàþùàÿ) ñèëà äåéñòâóåò íà òåëî íå òîëüêî â âîäå, íî è â ëþáîé äðóãîé æèäêîñòè, ò. ê. â ëþáîé æèäêîñòè ñóùåñòâóåò ãèäðîñòàòè÷åñêîå äàâëåíèå, ðàçíîå íà ðàçíûõ ãëóáèíàõ. Ýòà ñèëà äåéñòâóåò è â ãàçàõ, áëàãîäàðÿ ÷åìó ëåòàþò âîçäóøíûå øàðû è äèðèæàáëè.
Áëàãîäàðÿ âûòàëêèâàþùåé ñèëå âåñ ëþáîãî òåëà, íàõîäÿùåãîñÿ â âîäå (èëè â ëþáîé äðóãîé æèäêîñòè), îêàçûâàåòñÿ ìåíüøå, ÷åì â âîçäóõå, à â âîçäóõå ìåíüøå, ÷åì â áåçâîçäóøíîì ïðîñòðàíñòâå.  ýòîì ëåãêî óáåäèòüñÿ, âçâåñèâ ãèðþ ñ ïîìîùüþ ó÷åáíîãî ïðóæèííîãî äèíàìîìåòðà ñíà÷àëà â âîçäóõå, à çàòåì îïóñòèâ åå â ñîñóä ñ âîäîé.
Óìåíüøåíèå âåñà ïðîèñõîäèò è ïðè ïåðåíîñå òåëà èç âàêóóìà â âîçäóõ (èëè êàêîé-ëèáî äðóãîé ãàç).
Åñëè âåñ òåëà â âàêóóìå (íàïðèìåð, â ñîñóäå, èç êîòîðîãî îòêà÷àí âîçäóõ) ðàâåí P0, òî åãî âåñ â âîçäóõå ðàâåí:
,
ãäå F´A — àðõèìåäîâà ñèëà, äåéñòâóþùàÿ íà äàííîå òåëî â âîçäóõå. Äëÿ áîëüøèíñòâà òåë ýòà ñèëà íè÷òîæíî ìàëà è åþ ìîæíî ïðåíåáðå÷ü, ò. å. ìîæíî ñ÷èòàòü, ÷òî Pâîçä.=P0=mg.
Âåñ òåëà â æèäêîñòè óìåíüøàåòñÿ çíà÷èòåëüíî ñèëüíåå, ÷åì â âîçäóõå. Åñëè âåñ òåëà â âîçäóõå Pâîçä.=P0, òî âåñ òåëà â æèäêîñòè ðàâåí Pæèäê = Ð0 — FA. Çäåñü FA — àðõèìåäîâà ñèëà, äåéñòâóþùàÿ â æèäêîñòè. Îòñþäà ñëåäóåò, ÷òî
Ïîýòîìó ÷òîáû íàéòè àðõèìåäîâó ñèëó, äåéñòâóþùóþ íà òåëî â êàêîé-ëèáî æèäêîñòè, íóæíî ýòî òåëî âçâåñèòü â âîçäóõå è â æèäêîñòè. Ðàçíîñòü ïîëó÷åííûõ çíà÷åíèé è áóäåò àðõèìåäîâîé (âûòàëêèâàþùåé) ñèëîé.
Äðóãèìè ñëîâàìè, ó÷èòûâàÿ ôîðìóëó (1.32), ìîæíî ñêàçàòü:
Âûòàëêèâàþùàÿ ñèëà, äåéñòâóþùàÿ íà ïîãðóæåííîå â æèäêîñòü òåëî, ðàâíà âåñó æèäêîñòè, âûòåñíåííîé ýòèì òåëîì.
Îïðåäåëèòü àðõèìåäîâó ñèëó ìîæíî òàêæå òåîðåòè÷åñêè. Äëÿ ýòîãî ïðåäïîëîæèì, ÷òî òåëî, ïîãðóæåííîå â æèäêîñòü, ñîñòîèò èç òîé æå æèäêîñòè, â êîòîðóþ îíî ïîãðóæåíî. Ìû èìååì ïðàâî ýòî ïðåäïîëîæèòü, òàê êàê ñèëû äàâëåíèÿ, äåéñòâóþùèå íà òåëî, ïîãðóæåííîå â æèäêîñòü, íå çàâèñÿò îò âåùåñòâà, èç êîòîðîãî îíî ñäåëàíî. Òîãäà ïðèëîæåííàÿ ê òàêîìó òåëó àðõèìåäîâà ñèëà FA áóäåò óðàâíîâåøåíà äåéñòâóþùåé âíèç ñèëîé òÿæåñòè mæg (ãäå mæ — ìàññà æèäêîñòè â îáúåìå äàííîãî òåëà):
.
Íî ñèëà òÿæåñòè ðàâíà âåñó âûòåñíåííîé æèäêîñòè Ðæ. Òàêèì îáðàçîì.
.
Ó÷èòûâàÿ, ÷òî ìàññà æèäêîñòè ðàâíà ïðîèçâåäåíèþ åå ïëîòíîñòè ρæ íà îáúåì, ôîðìóëó (1.33) ìîæíî çàïèñàòü â âèäå:
ãäå Væ — îáúåì âûòåñíåííîé æèäêîñòè. Ýòîò îáúåì ðàâåí îáúåìó òîé ÷àñòè òåëà, êîòîðàÿ ïîãðóæåíà â æèäêîñòü. Åñëè òåëî ïîãðóæåíî â æèäêîñòü öåëèêîì, òî îí ñîâïàäàåò ñ îáúåìîì V âñåãî òåëà; åñëè æå òåëî ïîãðóæåíî â æèäêîñòü ÷àñòè÷íî, òî îáúåì Væ âûòåñíåííîé æèäêîñòè ìåíüøå îáúåìà V òåëà (ðèñ. 1.39).
Ôîðìóëà (1.33) ñïðàâåäëèâà è äëÿ àðõèìåäîâîé ñèëû, äåéñòâóþùåé â ãàçå. Òîëüêî â ýòîì ñëó÷àå â íåå ñëåäóåò ïîäñòàâëÿòü ïëîòíîñòü ãàçà è îáúåì âûòåñíåííîãî ãàçà, à íå æèäêîñòè.

Ñ ó÷åòîì âûøåèçëîæåííîãî çàêîí Àðõèìåäà ìîæíî ñôîðìóëèðîâàòü òàê:
Íà âñÿêîå òåëî, ïîãðóæåííîå â ïîêîÿùóþñÿ æèäêîñòü (èëè ãàç), äåéñòâóåò ñî ñòîðîíû ýòîé æèäêîñòè (èëè ãàçà) âûòàëêèâàþùàÿ ñèëà, ðàâíàÿ ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè (èëè ãàçà), óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ è îáúåìà òîé ÷àñòè òåëà, êîòîðàÿ ïîãðóæåíà â æèäêîñòü (èëè ãàç).
Источник
