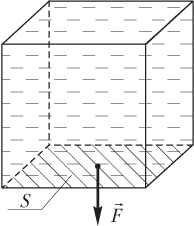
Сила давления жидкости на стенку цилиндрического сосуда
Рассмотрим (рис. 3.16) некоторую ограниченную часть твердой цилиндрической поверхности, которую назовем цилиндрической стенкой. Пусть рассматриваемая стенка находится под односторонним воздействием покоящейся жидкости, которое сводится к тому, что в каждой точке на стенку действует давление жидкости. Разобьем стенку на элементарные площадки. В силу малости площадок будем считать их плоскими и выразим элементарную силу давления на них в общем виде dP = pdw. Силы dP уже не будут направлены параллельно друг другу, их линии действия могут не пересекаться в одной точке, и их сумма может не сводиться к одной равнодействующей.
Для шаровой или круговой цилиндрической стенки элементарные силы давления, будучи нормальными к элементарным площадкам на этих поверхностях, направлены по радиусам и, следовательно, пересекутся в центре сферы или в центре круга (поперечного сечения цилиндра).
Определение сил давления на цилиндрические и шаровые поверхности имеет большое значение, так как в гидротехнических сооружениях обычно применяются конструкции с такими поверхностями (секторные, сегментные, вальцовые и шаровые затворы, водонапорные баки и т.п.).
Рис. 3.16. Схема к определению силы давления жидкости на цилиндрическую стену
Рассмотрим цилиндрические стенки, находящиеся под односторонним воздействием покоящейся жидкости. Определим силу избыточного давления. При этом условимся одну из осей координат направлять вдоль образующей цилиндрической поверхности.
Цилиндрическая поверхность с горизонтальной образующей. Направим ось OY параллельно образующей (см. рис. 3.16), а ось OZ – вертикально вверх.
Значение силы давления на цилиндрическую поверхность в данном случае определяется следующим образом:
(3.17)
где Рх и Рz –горизонтальная и вертикальная составляющие силы давления.
Выделим на цилиндрической поверхности элементарную площадку dw, на которую действует направленная по нормали элементарная сила dP = rghdω. Найдем горизонтальную dPx и вертикальную dPу составляющие силы dP:
.
Учитывая, что
И ,
имеем
;
,
где dwх – проекция элементарной площадки dw на плоскость, перпендикулярную оси OX;
dωz – проекция элементарной площадки dw на плоскость, перпендикулярную оси OZ.
Проинтегрировав, получим для горизонтальной составляющей силы Р:
, (3.18)
где wх – проекциявсей цилиндрической поверхности на плоскость, нормальную к оси ОХ;
– глубина центра тяжести проекции wх под пьезометрической плоскостью.
Для вертикальной составляющей получим:
.
Интеграл представляет собой объем призмы, ограниченной снизу цилиндрической поверхностью, а сверху – ее проекцией wz на пьезометрическую плоскость. Направляющие этой призмы – вертикальные прямые. Полученное таким образом тело называется телом давления.
Тело давления – это объемная фигура, ограниченная снизу цилиндрической поверхностью, по бокам – вертикальными плоскостями, проходящими через крайние точки цилиндрической поверхности, и сверху – горизонтальной плоскостью, совпадающей с пьезометрической.
Вертикальная составляющая Pz численно равна весу жидкости в объеме тела давления:
, (3.19)
где – объем тела давления.
На рис. 3.16 тело давления заштриховано вертикальными линиями.
Горизонтальная составляющая Рх проходит через центр давления проекции wх, а вертикальная составляющая Рzпроходит через центр тяжести тела давления.
Направление вертикальной составляющей Рz для схемы, изображенной на рис. 3.16, а – вниз, а на рис. 3.16, б – вверх.
Направление линии действия силы Р определяется направляющими косинусами:
(3.20)
Источник
Задача нахождения силы давления жидкости на поверхность произвольной формы является достаточно сложной задачей. Эта задача решается, как правило, графическим методом путем построения эпюры гидростатического давления.
Однако на практике чаще всего приходится иметь дело с цилиндрическими или сферическими поверхностями, имеющими вертикальную плоскость симметрии, например стенки труб, резервуаров и всевозможных цилиндрических сосудов, шаровыми клапанами. Сила давления в этом случае может быть найдена аналитическим путем.
Рассмотрим цилиндрическую стенку АВ шириной b (перпендикулярно к плоскости чертежа) и определим силу давления жидкости на эту стенку (рис. 2.31).
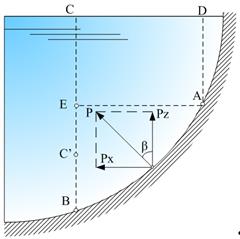
Рис. 2.31.Расчетная схема давления жидкости на цилиндрическую
поверхность сверху
Проведем из точек А и В перпендикуляры AD и ВС к свободной поверхности жидкости. Объем жидкости в отсеке ABCD называется телом давления. Жидкость в этом объеме находится в равновесии, поэтому составим обычные условия равновесия в вертикальном и горизонтальном направлениях.
Если жидкость действует на поверхность АВ с силой Р, то и поверхность АВ действует на жидкость с силой Р, направленной в обратную сторону. Эту силу реакции разложим на две составляющие: горизонтальную Рx и вертикальную Рz.
На выделенный объем жидкости сверху вниз действуют следующие силы: сила давления на свободной поверхности жидкости равная произведению поверхностного давления p0 на площадь горизонтальной проекции поверхности АВ, и сила тяжести жидкости в объеме ABCD. Эти две силы уравновешиваются снизу вертикальной составляющей Рв, В связи с этим условие равновесия рассматриваемого объема в вертикальном направлении имеет вид:
(2.37)
где Sx– площадь горизонтальной проекции поверхности АВ; VABCD – выделенный объем жидкости.
Если давление p0 на свободной поверхности жидкости равно атмосферному и находится сила избыточного давления, то очевидно, что
, (2.38)
т. е. вертикальная составляющая силы избыточного давления жидкости на криволинейную стенку равна весу жидкости в объеме тела давления.
Для нахождения горизонтальной составляющей силы давления Рx проведем из точки А горизонтальную линию до пересечения с линией ВС в точке Е. Легко видеть, что горизонтальные силы давления жидкости на поверхности ЕС и AD взаимно уравновешиваются и остается лишь сила давления на площадь ВЕ, которая для равновесия выделенного объема жидкости должна быть равна горизонтальной составляющей Рx. Из рисунка видно, что площадь ВЕ представляет собой вертикальную проекцию поверхности АВ. Таким образом, с учетом сказанного, условие равновесия объема жидкости ABCD в горизонтальном направлении запишется в виде
(2.39)
где pc – гидростатическое давление жидкости в центре тяжести площади ВЕ, т. е. в точке C’, hc’, – глубина расположения центра тяжести площади ВЕ; ωB – площадь вертикальной проекции поверхности АВ.
Горизонтальная составляющая силы избыточного давления жидкости при pо= pа равна
(2.40)
Полная сила гидростатического давления, являющаяся равнодействующей ее составляющих Рв и Рг, определяется зависимостью:
(2.41)
а ее направление – углом β, значение которого может быть определено из выражения:
( 2.42)
Когда жидкость расположена снизу от стенки гидростатическое давление во всех точках поверхности АВ имеет те же значения, что и в рассмотренном случае, но направление силы будет противоположным, и составляющие силы Рz и Рx определяются по тем же формулам (2.37) и (1.39), но с обратным знаком. При этом при вычислении Рz также определяется вес жидкости в объеме тела давления ABCD, этот объем и не заполнен жидкостью и поэтому называется фиктивным телом давления.
Рассмотрим другой пример и определим давление на стенку цилиндрического сегментного щита, служащего для выпуска воды из турбинных аванкамер (рис. 2.32).
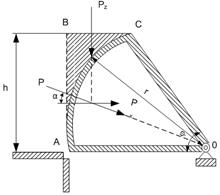
Рис. 2.32. Давление на стенку цилиндрического сегментного щита
Горизонтальная составляющая силы полного давления на такую стенку будет равна давлению на вертикальную проекцию этой стенки, т. е. на плоскость, размер которой по высоте равен h (глубине) и по ширине равен ширине щита b.
Таким образом, проекция полного давления на ось Х равна на основании предыдущего
(2.43)
Для определения вертикальной слагающей полного давления необходимо определить вес жидкости в объеме заштрихованной фигуры, изображающей столб жидкости, расположенный над стенкой. Этот объем равен умноженной на ширину щита b площади криволинейной фигуры АВС, величина которой в свою очередь может быть найдена как разность площадей трапеции ОАВС и кругового сектора ОАС.
Итак:
При этом очевидно:
Отсюда и, следовательно, вертикальная слагающая силы полного давления
(2.44)
Так как все истинные давления, действующие на щит, перпендикулярны его поверхности (а, следовательно, направлены по радиусам), то они образуют систему сходящихся в одной точке сил и их равнодействующая будет проходить обязательно через ось вращения щита, т. е. через точку О. Таким образом, величина полного давления на щит будет равна:
а тангенс угла наклона этой силы к горизонту будет равен
Если , то
Источник
4.2. Элементы гидростатики
4.2.3. Гидростатическое давление
Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление.
Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле
pгидр = ρ0gh,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости.
В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).
Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:
Fгидр = pгидрS = ρ0ghS,
где pгидр — гидростатическое давление на дно сосуда; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь дна сосуда.
Рис. 4.10
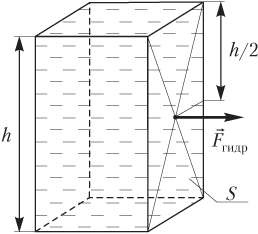
Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле
pгидр=ρ0gh2,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота вертикальной стенки сосуда (столба жидкости).
Рис. 4.11
Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:
Fгидр=pгидрS=ρ0gh2S,
где pгидр — гидростатическое давление на дно сосуда; ρж — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь вертикальной стенки.
Рис. 4.11
При расчете давленияна днооткрытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — глубина водоема.
Рис. 4.12
Сила давления на дно открытого водоема определяется произведением:
F = pS = (pатм + ρ0gh)S,
где S — площадь дна водоема.
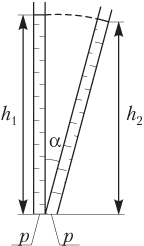
Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:
p = ρ0gh1 cos α,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h1 — высота столба жидкости при вертикальном положении мензурки; h2 = h1 cos α — высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.
Рис. 4.13
Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см3. Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.
Решение. Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:
〈Fгидр〉=〈p〉S,
где 〈p〉 — среднее гидростатическое давление на боковую поверхность цилиндра; S — площадь боковой поверхности цилиндра.
Найдем каждый из сомножителей следующим образом:
- среднее гидростатическое давление на боковую поверхность цилиндра
〈p〉=ρ0gh2,
где ρ0 — плотность жидкости, заполняющей сосуд; g — модуль ускорения свободного падения; h — высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;
- площадь боковой поверхности цилиндра
S = 2πRh,
где 2πr — длина окружности; R — радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямоугольника, одна из сторон которого равна высоте цилиндра, а другая — периметру круга (длине окружности), лежащего в его основании.
Подстановка среднего гидростатического давления 〈p〉 и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:
〈Fгидр〉=πρ0gRh2.
Расчет дает значение:
〈Fгидр〉=π⋅2,5⋅103⋅10⋅10⋅10−2⋅(30⋅10−2)2≈707 Н≈0,71 кН.
Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см3. Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.
Решение. Давление в открытом водоеме определяется формулой
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность воды; g — модуль ускорения свободного падения; h — искомая глубина водоема.
По условию задачи
p = 4pатм.
Подстановка указанного значения в исходную формулу дает:
4pатм = pатм + ρ0gh,
или
3pатм = ρ0gh.
Выразим отсюда искомую глубину водоема
h=3pатмρ0g
и произведем вычисление:
h=3⋅100⋅1031,0⋅103⋅10=30 м.
Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.
Источник
Æèäêîñòè (è ãàçû) ïåðåäàþò ïî âñåì íàïðàâëåíèÿì íå òîëüêî âíåøíåå äàâëåíèå, íî è òî äàâëåíèå, êîòîðîå ñóùåñòâóåò âíóòðè íèõ áëàãîäàðÿ âåñó ñîáñòâåííûõ ÷àñòåé.
Äàâëåíèå, îêàçûâàåìîå ïîêîÿùåéñÿ æèäêîñòüþ, íàçûâàåòñÿ ãèäðîñòàòè÷åñêèì.
Ïîëó÷èì ôîðìóëó äëÿ ðàñ÷åòà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè íà ïðîèçâîëüíîé ãëóáèíå h (â îêðåñòíîñòè òî÷êè A íà ðèñóíêå).

Ñèëà äàâëåíèÿ, äåéñòâóþùàÿ ñî ñòîðîíû âûøåëåæàùåãî óçêîãî ñòîëáà æèäêîñòè, ìîæåò áûòü âûðàæåíà äâóìÿ ñïîñîáàìè:
1) êàê ïðîèçâåäåíèå äàâëåíèÿ p â îñíîâàíèè ýòîãî ñòîëáà íà ïëîùàäü åãî ñå÷åíèÿ S:
2) êàê âåñ òîãî æå ñòîëáà æèäêîñòè, ò. å. ïðîèçâåäåíèå ìàññû m æèäêîñòè íà óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ:
F=mg. (1.28)
Ìàññà æèäêîñòè ìîæåò áûòü âûðàæåíà ÷åðåç åå ïëîòíîñòü p è îáúåì V:
m = pV, (1.29)
à îáúåì — ÷åðåç âûñîòó ñòîëáà è ïëîùàäü åãî ïîïåðå÷íîãî ñå÷åíèÿ:
V=Sh. (1.30)
Ïîäñòàâëÿÿ â ôîðìóëó (1.28) çíà÷åíèå ìàññû èç (1.29) è îáúåìà èç (1.30), ïîëó÷èì:
F = pVg=pShg. (1.31)
Ïðèðàâíèâàÿ âûðàæåíèÿ (1.27) è (1.31) äëÿ ñèëû äàâëåíèÿ, ïîëó÷èì:
pS = pSkg.
Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî ðàâåíñòâà íà ïëîùàäü S, íàéäåì äàâëåíèå æèäêîñòè íà ãëóáèíå h:
p = phg.
Ýòî è åñòü ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.
Ãèäðîñòàòè÷åñêîå äàâëåíèå íà ëþáîé ãëóáèíå âíóòðè æèäêîñòè íå çàâèñèò îò ôîðìû ñîñóäà, â êîòîðîì íàõîäèòñÿ æèäêîñòü, è ðàâíî ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè, óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ è ãëóáèíû, íà êîòîðîé îïðåäåëÿåòñÿ äàâëåíèå.
Âàæíî åùå ðàç ïîä÷åðêíóòü, ÷òî ïî ôîðìóëå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ìîæíî ðàññ÷èòûâàòü äàâëåíèå æèäêîñòè, íàëèòîé â ñîñóä ëþáîé ôîðìû, â òîì ÷èñëå, äàâëåíèå íà ñòåíêè ñîñóäà, à òàêæå äàâëåíèå â ëþáîé òî÷êå æèäêîñòè, íàïðàâëåííîå ñíèçó ââåðõ, ïîñêîëüêó äàâëåíèå íà îäíîé è òîé æå ãëóáèíå îäèíàêîâî ïî âñåì íàïðàâëåíèÿì.
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ .
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ — ÿâëåíèå, çàêëþ÷àþùååñÿ â òîì, ÷òî âåñ æèäêîñòè, íàëèòîé â ñîñóä, ìîæåò îòëè÷àòüñÿ îò ñèëû äàâëåíèÿ æèäêîñòè íà äíî ñîñóäà.
 äàííîì ñëó÷àå ïîä ñëîâîì «ïàðàäîêñ» ïîíèìàþò íåîæèäàííîå ÿâëåíèå, íå ñîîòâåòñòâóþùåå îáû÷íûì ïðåäñòàâëåíèÿì.
Òàê, â ðàñøèðÿþùèõñÿ êâåðõó ñîñóäàõ ñèëà äàâëåíèÿ íà äíî ìåíüøå âåñà æèäêîñòè, à â ñóæàþùèõñÿ — áîëüøå.  öèëèíäðè÷åñêîì ñîñóäå îáå ñèëû îäèíàêîâû. Åñëè îäíà è òà æå æèäêîñòü íàëèòà äî îäíîé è òîé æå âûñîòû â ñîñóäû ðàçíîé ôîðìû, íî ñ îäèíàêîâîé ïëîùàäüþ äíà, òî, íåñìîòðÿ íà ðàçíûé âåñ íàëèòîé æèäêîñòè, ñèëà äàâëåíèÿ íà äíî îäèíàêîâà äëÿ âñåõ ñîñóäîâ è ðàâíà âåñó æèäêîñòè â öèëèíäðè÷åñêîì ñîñóäå.

Ýòî ñëåäóåò èç òîãî, ÷òî äàâëåíèå ïîêîÿùåéñÿ æèäêîñòè çàâèñèò òîëüêî îò ãëóáèíû ïîä ñâîáîäíîé ïîâåðõíîñòüþ è îò ïëîòíîñòè æèäêîñòè: p = pgh (ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè). À òàê êàê ïëîùàäü äíà ó âñåõ ñîñóäîâ îäèíàêîâà, òî è ñèëà, ñ êîòîðîé æèäêîñòü äàâèò íà äíî ýòèõ ñîñóäîâ, îäíà è òà æå. Îíà ðàâíà âåñó âåðòèêàëüíîãî ñòîëáà ABCD æèäêîñòè: P = oghS, çäåñü S — ïëîùàäü äíà (õîòÿ ìàññà, à ñëåäîâàòåëüíî, è âåñ â ýòèõ ñîñóäàõ ðàçëè÷íû).
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ îáúÿñíÿåòñÿ çàêîíîì Ïàñêàëÿ — ñïîñîáíîñòüþ æèäêîñòè ïåðåäàâàòü äàâëåíèå îäèíàêîâî âî âñåõ íàïðàâëåíèÿõ.
Èç ôîðìóëû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñëåäóåò, ÷òî îäíî è òî æå êîëè÷åñòâî âîäû, íàõîäÿñü â ðàçíûõ ñîñóäàõ, ìîæåò îêàçûâàòü ðàçíîå äàâëåíèå íà äíî. Ïîñêîëüêó ýòî äàâëåíèå çàâèñèò îò âûñîòû ñòîëáà æèäêîñòè, òî â óçêèõ ñîñóäàõ îíî áóäåò áîëüøå, ÷åì â øèðîêèõ. Áëàãîäàðÿ ýòîìó äàæå íåáîëüøèì êîëè÷åñòâîì âîäû ìîæíî ñîçäàâàòü î÷åíü áîëüøîå äàâëåíèå.  1648 ã. ýòî î÷åíü óáåäèòåëüíî ïðîäåìîíñòðèðîâàë Á. Ïàñêàëü. Îí âñòàâèë â çàêðûòóþ áî÷êó, íàïîëíåííóþ âîäîé, óçêóþ òðóáêó è, ïîäíÿâøèñü íà áàëêîí âòîðîãî ýòàæà, âûëèë â ýòó òðóáêó êðóæêó âîäû. Èç-çà ìàëîé òîëùèíû òðóáêè âîäà â íåé ïîäíÿëàñü äî áîëüøîé âûñîòû, è äàâëåíèå â áî÷êå óâåëè÷èëîñü íàñòîëüêî, ÷òî êðåïëåíèÿ áî÷êè íå âûäåðæàëè, è îíà òðåñíóëà.

Источник
Что это такое?
В сосуде, заполненном водой, на дно давит сила, равная весу столба жидкости. Это вызванное силой тяжести давление называется гидростатическим.
Оно определяется отношением силы к площади, то есть его физический смысл – это сила, действующая на единицу площади (см2).
 Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Вставив в бочку, заполненную водой, длинную узкую трубку, он налил в нее несколько кружек воды, и бочку разорвало.
Согласно закону Паскаля, приложенное к H2O усилие распространяется равномерно во всем объеме. Это объясняется тем, что вода почти не сжимается. В гидравлических прессах используют это свойство.
Плотность воды все же растет при высоком давлении. Это учитывается при расчетах конструкций глубоководных аппаратов.
Факторы, влияющие на показатель
При отсутствии внешнего воздействия, играют роль два фактора:
- высота столба;
- плотность.
Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.
Сверху на содержимое сосуда давит также атмосферный воздух. Поэтому в сообщающихся сосудах уровень одинаков, ведь в каждом из них над поверхностью атмосфера одна и та же.
Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:
- внешней силы;
- веса воды.
При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.

На дно и стенку сосуда – в чем разница?
Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.
Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.
Наполнив сосуд, имеющий отверстия одного диаметра в стенках на разной высоте, можно наблюдать различный напор вытекающей струи. Чем выше отверстие – тем слабее струя. То есть, давление на стенки емкости тем больше, чем ближе ко дну.
Единицы измерения
 Давление воды измеряют в:
Давление воды измеряют в:
- паскалях – Па;
- метрах водяного столба – м. в. ст.
- атмосферах – атм.
Практически достаточно знать, что 1 атмосфера равна 10 метрам водяного столба или 100000 Па (100кПа).
Формулы расчета
Давление на дно сосуда рассчитывается делением силы на площадь, то есть оно равно произведению плотности воды, высоты столба и ускорения свободного падения g (величина постоянная, равна 9,8 м/с2).
Пример расчета: бак наполнен водой (плотность 1000 кг/м3) до высоты 1,2 м. Нужно найти, какое давление испытывает дно бака. Решение: P = 1000*1, 2*9, 8 = 11760 Па, или 11, 76 кПа.
Для расчета давления на стенки сосуда применяют все ту же формулу напора, приведенную выше. При расчете берется глубина от точки, в которой нужно рассчитать напор, до поверхности воды.
Пример расчета: на глубине 5 м на стенку резервуара с водой будет оказываться давление P=1000 *5 * 9, 8=49000 кПа, что составляет 0,5 атмосферы.
Расчет давления воды на дно и стенки сосуда в видео:
Применение на практике
Примеры использования знаний свойств воды:
-
 Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм.
Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм. - Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
- Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
- Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.
Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:
- выжимка масла из семян растений;
- спуск на воду со стапелей построенного судна;
- ковка и штамповка деталей;
- домкраты для подъема грузов.
Заключение
Такие свойства воды, как текучесть и несжимаемость, дают возможность использовать силу ее давления для самых различных целей.
Опасность этого явления учитывают при расчетах на прочность корпусов подводных лодок, стенок и днищ резервуаров, в которых хранят воду. Сила давления воды совершает полезную работу, она же способна и разрушать.
А какова Ваша оценка данной статье?
Источник