Сила тяжести в сосуде с водой
s7È2nbáý ÐÜ°Éu«ÀÖ
AMî^ÌDT4´3f”ù ø«
endstream
endobj
368 0 obj
> >>
/Contents 390 0 R
/Group >
/Tabs /S
/StructParents 0
/Parent 364 0 R
/Rotate 0
/CropBox [ 0 0 595.32 841.92 ]
>>
endobj
369 0 obj
>
endobj
370 0 obj
[ 371 0 R ]
endobj
371 0 obj
>
endobj
372 0 obj
>
endobj
373 0 obj
>
endobj
374 0 obj
>
stream
xí| t[Õµè>wÐhIW³dÙ¾¯$ÛÙ²b;$qF@bæ@Zæ×mdC ¸e*-4î@¡À#i ¡ÆÖßçÊ ðÿ½þ®¿Ö_-îÍ>ûûLûìé; 0,ÈD¢þþßbÍKý+·mõ~ú׳ H!&80¸æ¼µÞÐvð®Ù¸}à¯;¸À4 ðÞÚÕ+V½QÅJ²bì_¾+¬þN,¯Å²íy[/Ú÷¡î,ßc¼¹qÓÊ÷|:º Û¹cç¸hP¿É¦hîAzïù+Î[ì®Gúæp
Ü´ekÊÏ ´.§íWn8¿óXe×3Oþv¾{ÒÝ
ð£aÕ¥&à¢gèîhò¾*ß0ÓJJÕ>rPJ¥°÷üt6àøïy
YìÀú3ÂQ÷f¤Nò@Y:ÂZqnf ~xn§!¿fXh!s 8â70¤
Ú NàòAvè;,wöA |@Zár
p’äB’8 ¾{ɼÔûp9ü¬±÷DEÐzç ¨[àvb[tDJ½
#lkà ø#¤`ÜÊïÅQº`1zÃoÉ2rv*Úà|¸n
»à)8J®%ê2865±|vGêA¨ä_Ó>z65 Òß
£~ĹÖÔÇ Ã{IEɲB)¾çÃÝ°Þ$.RÆ6b8W.
}l>®q>{{Bö±ÆÔ½¸
X ÃpD&ÿ,u1Xp1éN¸~ð!ÖJºÙófêS@@ahÁ®«á§È¹_àû,1iÃNÞ”fÏgßÅ)8#ùd¹©gvðÑéËSAw(ãm°6Â#$Hdr6ö½¹¹f÷³orùÜ’©ÊÔ3 Òîp_¿ßëx^¤ü¹ã¯N]ëÀZÜÅpÏO´$Ø
ÜÙ%düÉf$¦=ÝÇßÚú.øPVâ°{®+à*xÁ_àC”Ø3=ëIù.ÙEe±KÙåìÍÌÝÌ=Ìý;Éù_ÌüværSøÆa .F^ãû¼NXâ!98Ò² Gê#äR²üÜCî’ûÉd¼O>!ÿÁ¸0çCÌ$ÍØfvûçã^çþ®^1=óôÌ’)}**MíNÝz#5¥BJ|=4¡tm@Ûr%ì¿ Ï
á»ÃÊ{áü¨Pܸ¢”
&ßSÎ,`3;¬Øö”ööwìÜv>ïÃücü1ÕQu@óÒÉ;¦ßu37ÏÜ*CYT¡äYQçbÐ2· OyỶÁ
È£ãw¢äì$_¢%ð¦²^ú¾’q¦a0xJK?Yg~/!;ÈuäV|ï ?”w!K~G~O·Ég¸’`fî¨9ãÛǬd.g®gÅ÷7Ì7¿0_°kfE6maװײ;Ùû(ûö.È5pó¹
ÜÜoqçóù6¾_É_ÏßÅßÃÿÿO©nRÝW½§Ö©ËÕ]ênõuꫪßT§4y(O¸úøò¹ÍEÝ$Åã¾ÆleÍü
àwâ
VA3Î>ÅüË¥»Ù¿°0;Ð7+ÍsѽOÂKüï9;ÿ¼ÀdÂÇhÀ®`~ÆÜƸH9[Ã]ŽVg;®óæ0£fö!Åx}p&qçÜYð òÿ¿yÚʼEfg $¿÷2á6Ø«I®n_À÷ÉÖKö£Ü
Ã$|G¾-ndêU.fªOè Yz)H}Zÿgr¼Á~²é$¸ÞÆS
ÄÈÍpø-Z¾¸¥öß`uðW5è38ÀÆ`wÏð8å^H1Úà[ÑVQ;j}( hEþ^&¹ÈÅß«^Ûan#ì8ëwÐ>et¬Ã}xSïÎÜ#¬J¨$çeÐ-ó!’u®ü~´Erjyê6¾ÃoÈÄO£õr!oæµ3SHù(êá0c3«`ýH¥ißÆïæâåÆ¿¬*PkïÀSüG¯á%+Àç(ë¨=
¨?
¸ùèÃ62½ìSÐD2am`>ÚíFäÁ2¸õé>ô!¿cD Ëágðjõ|%ίÁqÚáLÖ¬!¾ FRÉlÅù¨½íì®éMx-GJYW!©!Íxz+ásªË8C9tQôÉû¡
=e3û¼~ô®¨£÷b¿~
#dCÿ6a p¦3Uɬc”ôFªnôìsÉ®Âû;Ye3óp´Ñuñ÷¡÷
£g°3vn)&®ûuôd¿Í©r»5@n+GæCùyÁ_ÊõyÅì,O¦ÛåtØmVY0
zV£VñË(lZû½`JóçѲ´+V|¥¢?áŪ֯Ó$¼ý
÷ë2Rü’J9M)¦$·j
½-7ñr³ä’Ëõ`þ»ÍR¯71¥ä;ün%oÀ¼Ï¼-®µÍÞé÷¶$Z·ÝÙÒßÃêuMRÓj]Q!êôÕc.áG³(ÆÙR=ÊÆJdJÍ- ·ÔLW`-+V%ºõ´4{|¾Þ¢ÂiZ) ©1a
+$ФLP5%ÔÊ4Þut7p½w´pbç
ãÛÎX%Z±¼’Á®è¥sÃ8osÂyñQ×EÜÒÔsÍW[=ìÎ×:/-îÜy7±wQÏW[}4ííÅ1°/híßÙSßLl_âÅÙ«z{ä*ÒKwBwÞßj©
Öô¯÷&´R£´vçú~¤@fwgwäKÔ{¤ÞÍY£6عxû[öº¿ÞRT8*Ó5f3¯fVnSr
9͵/>ÍYBW$µ¡@$¼+½¸ ÷TIÕ°se%áÓK°WbȺ¶©§PMëiÿ$ïÎÏ %@úèë5+fkTá3 Y*’§E
ÛOåáp”¢”¢nÂ3Å5Ö)å²¢ÂmãÌiPð”BöAòvEouÙïóѾ~s±YÔ.{áOäH¸7ÁôÓS-ö3iËÈ©ÓÝû%äGÞì Mðô?à°¶¬NÇÓ¼:ÝÞ¾Dj_´¬ÇÛ²³·íÝ_+¥Û+O·ÍæÖ¦ÖÃÌæ«´¢P.?ML= .ÿTP¯WkP*âmMýóÓi¯Îçû;§Ñ^
ú²Ûì2Õá¯k¾VþÚò2v²¸`.È´w/Û¹S÷µ¶V´@;w¶JÞÖý;W§Fμ´ó Æ3y;[úOèxêë=ÖzqkI5J+£¹vѨL®]²¬ç7±k»{aú{GýØÖsÀFW©eN×Òðf
d4Jç0¢´rJ
R^9N@©Óª#°rI× J>TѺ{¾z^ô¡H0$=zFPCã£yF¥g5²xîtjîna$
EÇ{¸ÂÂÚéÚNáxmÇt-Ôc^8II±Ïì30!Yô²’eþ^nç»ð ~-ðI±|S® ·ÔÛ¥k«¥ê
cø%r%ɧ3ê³uN+Û©×-£ÉÖ:Ìölñë ×±E2 ^ |ñI¯È,ØÌfAb$o4ÙF³ÍHºÍÄ®sH>³áS2åúó1l#ä¨ &ÖépèÐÄñÙ#K^»88 î
NѽA9Ø
5» z×y®pç?îÎ쫾VÀ·¾6S#’ÌUf³Ð$n©W]cÖ|Gx±fâÏÍUUøÏÂ&Òiü«µP[«®EBÄIøÔ*»ÍépÚ}eååxs¤¥Ñò²X^0/eÙî_UÖÏú¹mç´w¬äý֢ܺéAÏB¯CÅdÿÕ$Ùqec¸Ê#hýÊ;¸ê¿?ø£BŪmüwòû”¤E©?óKù
xRÙÀÓêbYãi¬ÅÄr/f22µrkGæÕë3wy®ËÒl0o°l7o·g~@õ á>çÎ_{t*
Y#«W{®Ìz;£×ª¶¶y®¶>aRWÍ6,c² ‘6³¾-F~}6ko×¾3$h DQ;
¦YkÒ:F×ávïx?îKç¦z;
øxÇQ¨ªBvtY;u|
KÛlj¶Ë~GÊt4ZµQy. ª,Lô.c ´|Ãø/
/¿Ä >DabA)WEÇâ(WØU*)×ÏÅ,þÒ¨S©âæ»uø%õ˽säm?¿ïO3ûÿ5éýÅ®=ËÝÞß0öÆm·Ø?óÊm×]páÖñ_åuþH)Õå©gßb¨eÈv Tq^¡**×6Ç®/»I}G[7W´í¯”©ï/z¤öñ¢ç^ó½ZôZÙ»EÚ2uzu³¬Ç9 ù!ÜQv^÷k2JÕd¤î6îö¢;K8¨ëª[éè¯Ûì¼Ù¾ÜWý49R§Ó8ºê¶Ö°ó5Ýbgjè,Ï:«>©!ÑR
FáÂüpa XP[úpéÁR+[ÚQúÒïî)ýIéS¥¿)ý×Ò©Rý`))±i|Õ4£©Ñ¡¹Xsfæ~Í/5ÒhõfPÃÚ,Öea±` R3ÞñHqÉáÉ%ºú{ûO»Ô]¹NºXK6
1#ª½©P,Ör
ÍM¦` D´õÚaíÓZÎ e´ãä ,Èu#u×_ÇÔ=h’vÝ]~W~}ÊC
*(/KØ&þÏó2ßÅ÷óï[y¦k
xî:>þyÇ7×¢!8q4õõªpÛÑ>¦éãG
)3Ú
¡Í T¢¨ª^ÔµÆÚZÉæQ5Úf¸²]Ä{KQJ£ÕYN`9S ;èèUAc92¼Ú+U³9 dr.J®&J(ÎN?ãC6Å
aë(Á²Xy ,F9mdì¶ÙÚòÒ(»Ùæ@A®pRÑæUiªÒ(Óöðµ]ëÇISÎoefÛjêÏÜüÒùWÝá4êlLONtCs×2Ýö7d[v1_ÒrFéü+ZC·ÌüPö צöªyÊ+æH´ÒÐ:Êö¡ÜKðWù¼ÏTį%½Úûsc^#¿0j2!ÛRq@»FܦݦÛsõë#¶qæ Ûþ’¤çrÌ@ìV`Yxb`!èlx©óYí.·ëÚ]A½Ú7ÓÐq JÂXÔ]O±ìÑc&BööÈÜø¥Ê%f1YQõ,ÅûóñI5¡YYa©ÝþÊïQu£Ä{|ï8ºY±ISCBâ âCUC¿ ÄOhóP@á8Ú
zéSAK?{Nź°²ØøܦG.yíû·TÖthUN§Xën«h/éù«ëÒí$óù§¿¿ïÆeUÍ«êÝîÒ=Wþµ&^R&÷¨,í¶¸mm}µk»MÐ=ÀØM¹²Ã¹W°W?0¼g×4)ÑhµaЯÕÄy¯H«cä?ê ZÕü8ÉËÐkAzdCvçÆëò&
·/÷.×[`””@Tå¹s,i,Q,g ã'”¸}³¼Sáï¥Ü©®Ãµ
ÿOSÇ}/)j*p9ÝNFes ÓæÈ!9fOqÚ1ÅÂèÂô/}iíÈC±àY©c§ÉÎƧSÚe-+jÏÌ=c|û䳦úÞo?v)æ«!=±qIÓRÇï½üéýý»ïºH´öÞ!áé,ÀÓyOÇ >Ò-»^È$yIJTc¨AµV£Ï9ºi#rh 9ÂeJXl/Sм4ªWÐXÕÜŲ%uBÄHK¥~fÑÊíÁøÉd-EÔý,CS¼«wçâ#æU¹ÂtÃñ´tmVLÍ *ãSÖNQP8ÛLPÁãÍaT6«ÝʨTAOVf;Uqh-9àRgçs1ä°ÆbÕ9s wæâtÃ’Qg¾¿$T6Ò&lÏàUÃà{Dµ+c0âþ%ó¼¨VMî]êÃiKúê%x|Qª:dg®J1lÔÖWéwÞê_ýýÑ÷¶9úùsrò¶` }æ²÷v¾põÝ$ÿIx^ÇÛ¿Ú·À;·øζSýÊYÀ!!äBlÝƤÂPÛ,ªµ`VY#¿¨’ËúâUÏI¿h¦eTt¥Sm¶¨,fU (êUj£P@
dO¦¥$}¾ÕÌQ,£NvL0Å%rIWÉ` WbI«KÈ`3HqÑ11Ág¸;hÂÖÈÀaܾú:Ë«à¤S¬G.÷ÖbJ 8ªU-M±5b[[KâÊù{
®w Ìæ
]y$I(³(ägò fz*¿?/&ÑdØ53.ä¶ÚÝÙJyÃá«l7H7ÛnqÝs[îþûm?Î}È¿ßö¤ßÒl’T5ã8^o@ñ]4hÆ0hÏ^®SjOÍs¡QaÉ>gqëôu9¶9äÚÒ¶³Öü¸çì¬ïhVun¹«
Ê«úfîsÏÙϾ±²2ßÙñÎßûðÜÌ{/®êþèÓÞ©ÿàåê0û T3ÏÊíyÙ·LfPÍXÈ!ÕT³£M27o/y®Õ hh§àâNZvëEuúU«UîXY0 øßOuQoª÷K*zú#VwýíåO3sH$;G4D²¢¡ÚE¤Ú¤6hDµ;;Stû¢¿¼ºB,BETU.StIb®(EbbÙ#p*%Ü{“Då”OFØHö-¦Gª¬fWßPý¹]jºÆ´§Ín5UÛL¦ê¢Y[øòÕ{ì픲¤h¤è¢ßqEÄbÈ·Øbr3¹ð×?Ùnñ
ñ&ñA»Çð¦á½ÜFöOx;;Ç Ú±Z¶Hõ&b2”¦jN$¢AÕu¤HÌ6Fu:ç./óK*·KÒí¨ejqI̱Z§3òh©þîú bÄÛ_N2²;û)EÌ
PAuëïÓ3Ñ:1.£³euó»a*еµû³jh(|±cN8N¡´NÔ1¥±-?M9
NfØêÉîÅ[`rÄ!”(·E¯]¿øÿ®ÅOe[¶KgÄ#Mrh¢ØL!iþN$îª}«óFâafIÞgp’rfY¸%̬uú59ëçñmxß #Ô`¢Ù$VÇ©K(jLZÓ>°
*¦½¬:©^)5*9ÿîîOdúó¹ÙÞE-Æê+¹±yhcÇ];ñÞÓð¬»-Ø%ö¹ë¹3/Ýv2~?ï°fÕÞººÅ`Ea5ùýí{6Ð @,jÁ$¨#×_hÏÆ{,3ojy¦B¢AvDþ©Õ^G¾°À0?³7s§gÎúÌõµs®ó{~é1æ[ómPÙ
5ª5ê5·F3_upTCÄ1ª2Ô¢Êîvvþ$yÑ*ÚBö¼|Ø´fºmîÁepÔÎb8_$Óm4dÚ?ÍÏôÞcòc·¡=âU ï/9Rr¬U¬ºÁ+A6Ù#vÆ>NXÙÉxóbyÍylÞ¾0ðÇ1ÜÁ+HZ7S³¬|¡èhÐIÅ
@7-U×hæÃÆS_’hÒÿÝ× ¼¬hji¤aP’ÁÙCÆS·Z¿ræQÏ^%3íZɧ3¿knCþZÝ{^MI©SÝ¢Ñüò óØ¿Ì7â¹æº37Ï-5B&àçN·Ï¬íîkª>Cn
êõÙ¡!:õq ýM©?³òÐÿ@nViÚÞì5Õ¶5ùÛl×Ø4U1ùó%ÉQ¯aÝYù²C2×Å1ÍtK
:´z½Ø¡µô0ãä/².=H?ªºÝÅæÒHi$>}T8Ѿ¨’1Ù;Ui_Ü3=´45WEÌ¥P_TúÌéhiý¥*2UURC$n5*
Ôü6¸ò^+Xc/M°öQ¬mOç²0&A`¤@ Õb³Y,6µ¶ËÚRë3F1¦²²ÖÖf¢®ôHÐ% i¥ÚÝÞfkoo+THf¦)j’
±úy¤f7/j0µ·qK:KüùþÂn?J@^¶.B%K
¡¾ â©G½hà`GO=’,ª4] ëJDt¦fS«Ø,¶[ùÖæ2®»,`,-`á-6)À¹8ÍÄü£ñÔ¤¥7Åãtú6Oó½cÑÝãÚÛ»ÚqÝ#µÇ0Þª5-^Æ.’¹,Ò¹§éìä¼=Å=LÔ]z})iK”Ý{ºîî~× q¹&QhsL:¢;@4Ð+FPO1µªÓµÇãô¢^övè]TbÚNýÞçÓ³JÉ¢´fNcÈØúZjzk#ñ£èÑ”ñ¡ÙokKÑA¸w*]> QÒÒUÔSEWü¤ÛL;
kiþäòßTá¬tV¦/3ñ¡¡¡ÍJ5«DJÖòò
¼^*ß¾ê!¥§§ÝE¢òÓ~òb=É0cyTåìä³H ëùñükG 묲”wÍÍñ¡æeg´-4-ÆÈѹÑ6a~M㪺â>Æ_.=»3t±=ÞÊR³W>3pGzA©¡öÆ3åæêú¹ÕÐ÷Û?o«F×ËÅz>
µpFÏü궫+nø~¹¡ê¬Ï
3 ÙUAfþ8¯@ :Ú¾ãL´qAâ}ÌäòÅjãüEôïÉ©åÎ@ëîr:[yÎÆóã]>¿ú
!æò;üF¿9×Ïú¦ÖJk¡áók=ÖAÌ2«@ j¨ÕeõÁxãÌërÀ%påæ¤D.1å.ÌíËÎÝËwåjór;ó-Jã4ñ”O!Y+É.à aÄÀõÈÓIc ^É
yèEâgÈñÚY+.Åk©q¬U~ü£à£SḔ>GÃSôËî5sÂ×|çÙÙ]Ç»ÐÊs4%*úu
E¢ÌL¸:Jý 3ÆU§²èyìÌöe3ÇɲUñ:òf,dP¼YÔ®&¿)¿
ä.¦á*ÏTÉÕ$ÇLÿdIe ÏdÉ´¥äzùµ>O_¡g5BSk,YÉ褼ìÖÌmN$Aø+Åùâ
ÒuÙFÓêvÚÜn§_ªHtmÅlÎíä*bï/öCÐñUémÂ`,%m,5Sþ^
û
Å0¡Óp61è³=Ùd_Í])ÞýpöÙofý©¨©ÍÌò1QÊösAMv¸c6¢
o ñQÏouÅ(~gù|e¤@ùr«7Æ
¤ ¥o
A&:!É”³QCd6jtÆf£2à1S³Æzá°bnè§{grôbf /NmÌÐÔ)óQ¥¡ðiãÿOf~/!ë)uÿª¶§MCZÝQ0¤(û©Dç,;ï
ÛZ*[yóV½ ·µcæÖjC%3þHuQ-úW¦òìwÛÖ|So[宬lÍÛwmVÈ3′{PlHñ¹L~¼
úÖÔ1.JõNÊÖ¶B;Oû¢óR
6ìÄN¹ÕØSp¤RÁòdÝl×ës©sòùÝþì A§jͳÄlU¶¤n@m=×e%V«dúWâPIåÜç8Ày¹CÇÉ-óbÜTÆÉUÕ)+Ǥ¸p&yùäú1É1Ì1n|,ßÉgâÊÉÙm÷)Gy4LÃuê¦N~Ô(ÇEOv RI;Ómù[áeóºVÌ«Üà,,Îe+W
ª$²ùùÌ}pÙú¹;jn
ZêÅFb|Íç!¯ýÄ-¿á gÑß´]d¿ÜÎÞn»üý#y 6r&aTÄAäc¦ÕfµÙb³9Çî°ÙÖîÐú-~§ßëÏÒø}~tÆaeI)3[4ÚìY:Þ/Ê,QýÑFìØåFÉÒj9ÐÒ2&íBmvX»KËwiV®¨i;¦ ñHV/dI²·Ë;èñr}^Rì}Ú;áôr^ÅLVż/ÍäѸp2m$g¹U¨ô&9|PNTÙfþÑ)z
å©zhP=ø´zmSí°ZOÙÀS
@$ò5uÈk#×LMïTÌ WÏXë¢3OÎSÅ>0ý$Ó`kÎ>¸°ÊºÜÁ,=yIMßÛPMO¤f>sfK
{Êkuãá¹4ÓoFÄ£ËñûýyT´MÁ ØôNhת¼ãQ1·÷y÷ ;QfPd¦èBgðg¡§Ï3ìÙåá»ÐBRäé,Ò
d4åyL^ÓDoÜÇõqäin]ã¬â:éOþAD¯3
G¤¤¸4íSNyäY:û5úÓZSCÞZò-Í¢ù3Ç¢%L]Or«øÌÏ?omª¦ÒÃõ÷Ìǽe«ÏþÔcõÅÊrö8(åÙèa¹UåQØãN¸s¿òب£&%£LηêUÊc[t÷¹7¹ÝÝ*÷8;Gb=öôÕl8b`ºÄ`àïªhH.±Z÷X’l=beË£1ÐܤÖ1ºì4J’âCx©A~ÒO&x¯¡Ù©w+þC@íCIqÚ5Ó;8eý±Ú”¦¶(~î {oÀÒº¾¯¨6P·ùqë¦ãÇW-^ÚWM®Ì~Â]/W¸0û]Ëg+¡Ü!B0){zÛ5_+`Àcôë8Ð/b0i
(kæ`C É$è%³9S£uºP&)ÈrªàÐÓ¡C!6D&þt¨
u#cñD+
ò#|g¿ñ:Xè¡ô¯HÄP¦´ÛAÀ1át°?¢,úRö>::þôMSÑCëz2|Zþèo_SÞ2jOe_séºB)se¥¼ÜfïoóùëÉï”ê¹èÅøØÒéW7Dt.ºöC¹cÙÂËúJ5ª(~m,~¾´J ·ëäíIä¥DHÊÕ¼Ec³[¶«³¯U¢×îeÑÄNs%&Tæ¨N’è5¢Vå Ró)?¦cÆPlgËe§d£5U6ÂM ¢²Ül$ÁÍFâfûPq½éHâ+f°6ó#azêÝ¡°òbúº
Gû4ަ㥧Ú,{fCöÔ×êp%y«6oþñ¿½ùÚH·sK@3w1SvF6Ð6yøúK¶î$ÏÍük³wÃÙ?å×ÿø>õ·Þ>SígFùó»ß.£Ïøþ߯¾A MÒjzP¤Ô¾X*À߯ûâ° §[fæBUý2åF}Ü$àÿàÁ~Ëþ’ aþÿDÇ¿@¿ *xÑ?2·ú»Pð?Sýã®þ?/`¿ÜXxá?ØoÒçÍömÿßÐDÌÿ÷Vûíóíóíóíóíóíóíóß=§âoz¸ª,øGcoc6®àèÿÍ£8Cò/Ó
`ùNå6Eñc°CàTAã _Aoÿi¾ECùÿdàûÊ?ÿ²ØE®;ô__>¡ýú«Ù¨]÷íûíûíûÿå;ôÕWßðjþÛWÀ÷IÝúnýrÃ|ÿføIg®3ÌQ|«ÍæÇÌOáûù9ËÓïqz»e.^`a.ýOîhñ#pæzk¶Ñ»¯oª,ZGú8¶Ìæ Ú¸³yðÐl
NÍshU³y¤v6¯ÂúÅÐ
kalïlºa 6Áù8®.TZWbzª}+¬ó`)6#íf¬ÝÛÖó±}+ÖmÄw5¬9XÛt^lÙ¤vR¬4ÀbX]Ð;ã
Öá«Ñ;_x1ö8Ç:
j¸
ëVÃc£2oÝ
ÕÿäXÕPo ®±Xyÿ¹QζÍHµNáwv¼n,åDéòÑ¿Ùò_Ñnï81aR´:£ã~,ß+Î#0GèC`ÌYÊã6§Ñùi´>ºKå’p¦&8ËÓ¥ÕcºèÅ–ËJå-gÆMS:3nQÁÉ®R¥¹byéÚ±æt¯ÆtuÝ,qu©ØàDzAFDØpA
«7Ca7B
SJnaÂ^#VMSjjðp¶ÊÞ”,ô+ÚPR§A®h`!ÂN
§KÂFñ µ(+eÇÂsÌ/*
É̬èSËÜy bI:
$g3åéÌX¨(z¸AaÍ’òÓ½ÆòçD=eÂÎZËl8;=f²FåýèB` ÁÂØÏ`Aò}É¢:»oLg
Hÿ xFXØ)QÊ2¥ÿdÌê Ãÿ[ÒdVúNÇÒ1Áíj°±oâz^dì_ç ~q6âçÙ_AYç½c&!:óÝä÷°Û1ÚÙûØ!øAö2ð(dJÓóü)6èØØK-ìx”»ÝÞì½TÙÆ´zº¾=úû>»lHu©¢é)ö| Ði
ÑÝ
ì8nsÙ”â ìQRý]Âù~ÌÐO®ì!ör°#~Ý´ÙϲtïnÆÆèD½Jû)rüSe¶ãcÁÊ(4Ù A¦¾¹·©AÆðµ¡aÂ0Âêí¶L!M}Ù7`7ÂÌs8äö$rðñçG°ßa/ENwk/ÓéÊ.MZ¬
Ù¥TÁëb_
.þ5ª²ßS¶²{Ìå¡þÔf ë.Iv¼ÁSì»CáÄå
?ÔÊ?{
Ò95aãéwcq¦»&>Aà¬÷Ð
},wMQÓAvÒ¹-i,bçãÖç+Ü´ç*k7áLIONôg4Eè³¢S%#â¢l;ÊÏB¶3¹Jĵ/J⸴cçXeu´ø Û©ð¢3)Jéê¤ÕdZÚ´5éÌt%Í
a8©1*ÕáYdCc6gTD9Vv[J=&[ÇWGSzRªFtL° ô¯b£Ê¢Ð°!ÀáG
#J-ÇíC
ų-chjبGØ
ð4Â^©íG`°¾gèÇt7#F°,`*#ô# ìE@8 ClÎSÔÅ $#pxV
¸Bl³°^Ö 0ÌÜ&Wa&ÃÌ0;Ì
óðY#
£òzÌ¡I>&ýÚAí-ÖÊÚ.-+h½Zþ÷ uu)ý9EU]úzÇ_t°ÝªÝjæPC1ÃaOX8D, XäkØCuë>©cuîø¤=ôÖá·>y=Tt¸è”VîðTG+úÈ&2LvN$RO®Ýij»XNd#l=ÊׯÔèÙb½¬ïÒ³Þ«gvë÷êú ý¤¯VªIÕÕ1ߥêW
ªFT»U{U*QQ׫ew¬¡yºÓ#îVrÒ2é¤RÞû1TÊ2¦]JN´æ$ëu¤Át7¥£e ÓbZFкÿ ë1ÝÀ0³rý²ü^?~rÌO&ýGüLÂ?ág&ª×U¾«|MYåkØó5eî×pÌ!H¸ÚWºWîU
îU¤£¹oªëÇtPÉÉv)9 Óbc^MJ¦’sØéÃ,D0GؤDJÁÜ©ÌÜ>W¹=D(7rÒ(KAcîÌh_¹¼¼¡%¡RÌmÉfJ{[rnUn¨@/JrìC“!¦{Óz%·O¡1.’0=¢ä1Ý{º_1=ÕenÇ÷6̱öbYÏÃ1Ŭ±3O$×YÄqæÑd¾h,5Xyo +éOtþ@I*©IÖKÿÏI$CY ~¬>¦¤ï+ézÙè7¼ç7$oC.6øäÌÃ;¹Í5Æ&¦ä%Í^ÃI¯áÏ^ï½_z
wy
½^CµÉɧèO
äN%½EIËÄ!;fxAËDÎN@{aÈÙ“uÉP8ÎjÄøDYÉDdÇbDÉͬÉÄ-c”£¬j(ÎH.Çf}i¡sñÉP8Nf! ÑßÙ¾Hä :!ú¢’ɿà ÿ&~à Kþ
ÌÃÇõHýxzvò(Ô V’1ê£d$C¸8ò`2èdÈèþ4º’ÝèGÉýKrà(¢Ûùéx·A¾2ÎTðdtÁdGѦdG¢
ɺKÖ¥]×QM ¤¬tEr Í}³C¾Ò¼Êç%;(KZé
Ò2»fÒDc>ÒHFQäd¨Éê¡ ¢¹iÎÕ&Â*ùÈcRÌÿr®|vz>O?.$%C#(@hAä¡=qQÖÙY-P§,ÊQ*!ò?#zPFÔAܾ_Æqÿ^7NÎJ_Èã?ÏG´_ü¨ãñÃqxÅP
Þ/FÒ·ê0+ëÅ7CGÅ7rÅ_
Bö/æÏ·ãùűq8WÜ7 ðÓ vKæ3{ï8C¼5o Ó5ÜÄ×Ð9p «BÛÅÁËÅP¶v’n eùçëóéDNq]h±¸7²û¬X#®Ý$ö)+>’ô²¸¤LÙCû²£¶:¥aþÀb±W
õ´WPrÅ®sÊRa¤Ò4ö²xfÅza2°Y£~J}úu·ºýM: ö©sÔ6E#húKÓ0Ð c£¿”¦?¢¶©TM9%/04¥? ¦w|¢a𢰲íLûÆDE¸}Z¨·’4]g÷ò½^ÒX íçz’HãD·hYIÂÒíÝ.$N0×èî’)Úã*ýsL«¾ë¡¸õªïööc[½«ÞRg®jmþ¤6miþòWÖ®pøk¥ìÄÍíKze÷&¢4ÊîmOÐ?ÙtÙȬoi>Àl ¨·ç YËllYLëÉÚæ^$«QÈ ÙdÐA1Ë¡aýò¯Q¬n«K-$£f¡B´,MÔôU”özÒ¤5±×+D?JOÂuà2EHÆo2aߨ¹(Ùh0#
)Éh4£Á¨Ò¼èËæütóOÒÍ?¡Íã|Ù^L¯6ÊA&iÂÿÕÿD’26wÛù=ôOmõK-«ú×o[ëJëõ¿möopûÏ]¹â«Û¤ÕÍó¥fïèÜohî¡Ís¥æQèiéîíW7’çÊs[¤Í½cW}m®ëNÏUyù7v9¬ÎÕ9ô
ÍC´¹Î5Dç¢suÊÊíI{WϨ{§ñ£×¡¶ô{|½a°NQë2ÏAîMdH m*j(j M¨Ò´ÉHÿÚlë²ç òàlÕf©¶ºZÖ5ã¿-ølÝz>Èã-[Ò¼v¥¶[v$عʧ°E©mß
|ùÃiZØnêíèhqk¦9dÆÝáÞ-§’çÄ]+¾C ôõ*Gé+ït|ÖÁN(þ$Â%ÂÀè~áFø9ìDÝdÝ:v¢c²ãÒ¾5ùַآɢ#ElÅì
èT½Wøå{AxË[?ý¡ìVÙ7].3tקذEiت0t½Ò5
OwÙn¼@é®Ýò¥c~ëáÿúÌÖ¢ þ_ñÒ-
endstream
endobj
375 0 obj
[ 0 [ 778 ] 3 [ 250 ] 17 [ 250 ] 26 [ 500 500 ] 570 [ 722 ] 577 [ 528 ] 587
[ 722 ] 602 [ 500 ] 604 [ 540 ] 606 [ 506 444 725 ] 610 [ 576 ] 612 [ 576
561 681 576 500 ] 618 [ 556 444 491 500 ] 623 [ 500 ] 625 [ 564 ] 630 [ 529
] ]
endobj
376 0 obj
>
stream
xeMn0
÷ÂËtÆ,%Ä¢?*í=¤±³àöµ=I6ôyÞ3v×*iIüf&Þ%TÂÀr£TQÊÜ)|ùØë(væn-¦¨,Iüî³5YÕb:ÀC¿Fª#Y}6ãî¤õ7 ,I¢ª”è¹×/ý$¶u+\Úeí¡SlOfÝs0½:BT&nU¤Ü»UE Ä¿x®ÃÀ¿zÔS’ M*G4«=±¥H¤Ç@4
£2CeÞ ÑPó=½Ôº´Fó’/£EjvVc-(ʶ·Ié]ÒaÒ-ªëÐPQãá.²äO¥ì®ÒeyðnðÚ¯½)Û.üõó¿Nq$LÊÏH*¸¾#=iïòû*¥·¿
endstream
endobj
377 0 obj
>
endobj
378 0 obj
>
endobj
379 0 obj
[ 250 0 0 0 0 0 0 0 0 0 0 0 0 0 250 0 0 0 0 0 0 0 0 500 500 ]
endobj
380 0 obj
>
endobj
381 0 obj
[ 382 0 R ]
endobj
382 0 obj
>
endobj
383 0 obj
>
endobj
384 0 obj
>
stream
xíý |TÕÙ8sî}»³ïûÜLfÌL Ü $Y0vÁÄ5TKµUÜ-!,°}µ.ÕJ߶Vm-´E«Õ´´EëB&¿çÜ°Xßïû¾ßß÷óý/wnÎrÏ9÷Þsç9ÏvιA!¤F½ABËDÊ8óMPòÎEë×úrÉßFǽ·tõ²+ÿíQ7¡#$-[¶rÃÒÔ³ºÒÕ t]éò%ÿ&ºâYn_ ×W,Ã_UPû#pZ~åÚkÞXleáüU¸Ç+W-Z MнÇbsW.¸fµÂÈ
zÎïªW. üÛSp~úpdõª5kGBh1B;¤õ«»¬Î~øªÎ>Ô#)Ç;É%ߤá
>2»ÑRbÀB¤=G¡kêà.
hæÔ >$ Ï(¹-×Ó2?>* Wß-BXÉAÞÁÅÜüôoä£ÓÈYÉ
Ì]1r1Bûg
!Ýv¡:ËÐèjB¢:ÔîFÐ[h/Ò¢
ø§EA4=xìE5 + ûÑ»èRÔ>@’QjF¿Ã¸O=Z,(;ò1ÄÍèÖÃÐJ& ¢#x%Lâ8Oî×´¢¢7GÞ³ï£phd¹EPú2 +Ðë#g)ÐBôÞ?F~Ô¶³vÛÈ
4D¿ÂÍ6HÞQD+᪱91ò’ôc£%p§ÐÐãt2$»ba4MC öZô.6â2F¹JC’1òFý¡F4Ýh¼N¡Ï°
ãïã§àø9þäè[3Z6~ ÷zÆe¸X eEQ4êúÐxþ~t7ãv|¿Àì$sµ#¦óÈ Å¨
z¸½ Ï8ÐÀµ¬]+I
_o¸=£C?~pÿ}áø=¹ôÌy|äèyQºÍE«Ðzt5ú`õEôúþ( å[ìËÓ#wlÃhZÏ{o,
A8Þ·Ôc¼E§ãe¸ßñ»ø]”%~ÒEþÌô3?e~ËVH$#Õp’òÀshZ¸ }’¼ïãèeô6ã0.7z®ÿ!áx¼E~ÇÜÌô±g%·äNæ>É}=²
ÉÊ&Ö¡’
ÅèC_×à?BÏwá SÎÔ13væVænæUægl7ûû¤Q²@òlAîªÜÏGGnX`$
~EPeP%ÐÏR ¦Ð¿Õpt£Mèz´
Ýôr’Ú÷~½~
ÞGöC/§_ Tw3¾ûñÓøü2~
ÿN£TZ24eäf8î&ÇÉÛä#ÆÅ,bz^8v2wYIJì$ÇdÉvÉcÒÊdeåo.nþ]å¹y¹{r/äþ42{dôG%¨zºzy?Ðà8J|ð×b_ÿ ÅÛp¨!X«Åp#Sñ%pÌcǼ/£÷âðø&|;þ®xÜï¶?Áñ,>ǯð ü!þ3þ;”&P3O”$A²ð¦È$ÒB¦Ã±¬c5é&ëCýä0y12
Источник
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Закон Архимеда
На погружённое в жидкость или газ тело действует выталкивающая сила, и равная весу среды, объём которой равен объёму тела.
Выталкивающая сила (сила Архимеда) равна
[F_A=rho_text{ж} g V_text{пчт}] где (displaystyle V_text{пчт}) — объём погружённой части тела, (displaystyle rho_text{ж}) — плотность жидкости.
Плавание тел
Рассмотрим тело плотности (rho) и жидкость плотности (rho_0). Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести (mg) и архимедова сила (F_A). Если объём тела равен V, то
[mg=rho g V,] [F_A=rho_0 g V]
Имеются три возможности дальнейшего движения тела.
Сила тяжести больше архимедовой силы: (displaystyle mg > F_A), или (displaystyle rho>rho_0). В этом случае тело тонет.
Сила тяжести равна архимедовой силе: (displaystyle mg = F_A), или (displaystyle rho=rho_0). В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
Сила тяжести меньше архимедовой силы: (displaystyle mg < F_A), или (displaystyle rho<rho_0). В этом случае тело всплывает, достигая поверхности жидкости.
Таким образом, условие плавания тела можно записать в виде неравенства (displaystyle rholeq rho_0).
Два жестко связанные друг с другом одинаковых бруска, имеющие толщину (h=5) см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.)
Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
(displaystylerho_1) – плотность материала, из которого изготовлены бруски, а (displaystyle V) – объем двух брусков. Тогда масса этих брусков будет равна [displaystyle m=rho_1V] Сила, с которой льдинки действуют на воду, равна силе тяжести [displaystyle F=mg=rho_1Vg] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда [F_text{Арх}=rho gfrac{V}2,] где (displaystyle rho) – плотность воды, (displaystyle frac{V}2) – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: [rho_1Vg=rho gfrac{V}2,] откуда (displaystyle rho_1=dfrac{rho}2,) то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину [frac72h=3,5cdot5text{ см}=17,5 text{ см}.] Глубина увеличится на (displaystyle 17,5 -5=12,5) см.
Ответ: 12,5
Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна (displaystyle rho_text{ ал}=2700 text{ кг}/text{м}^3. ) Какова длина ребра куба, если выталкивающая сила равна (displaystyle F_text{Арх}=33,75text{ Н}?) (Ответ дайте в сантиметрах.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV,] где (displaystyle rho_text{в}) – плотность жидкости, в которую погружен кубик, (displaystyle V) – объем погруженной части тела. Так как куб погружен целиком, то (displaystyle V=a^3), получим: [F_text{Арх}=rho_text{в} ga^3] Выразив из этой формулы сторону (displaystyle a), получаем [a=sqrt[3]{frac{F_text{Арх}}{rho_text{в}g }}] Подставив значения в формулу, получим: [a=sqrt[3]{frac{33,75text{ Н}}{10text{ м}/{c^2}cdot1000text{ кг}/text{м}^3}}=0,15text{ м}=15text{ cм }]
Ответ: 15
Однородный цилиндр, изготовленный из материала плотностью (displaystyle rho=600) кг/м(^3), с радиусом основания (displaystyle R=25) см и высотой (displaystyle H=20) см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)

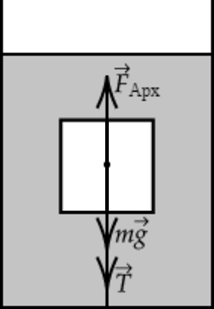
Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: [vec T+vec F_text{Арх}+mvec g=mvec a,] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [T- F_text{Арх}+mg=0, quad(1)] массу цилиндра можно рассчитать, исходя из формулы (displaystyle rho=frac {m}{V} Rightarrow m=rho V,) где V – объем цилиндра, который можно вычислить по формуле [V=pi R^2 H] Из формулы (1) выразим силу натяжения нити T:[T=F_text{Арх}-mg=rho_text{в}gV-rho gV=Vg(rho_text{в}-rho)=pi R^2 Hg(rho_text{в}-rho),] где (displaystyle rho_text{в}) – плотность воды, подставим в получившееся выражение численные значения:[T=3,14cdot0,25^2text{ м}cdot0,2text{ м}cdot 10text{ м}/text{с}^2 cdot (1000text{ кг}/text{м}^3-600text{ кг}/text{м}^3)=157text{ Н }]
Ответ: 157
Однородный кубический предмет с ребром (displaystyle a=18) см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна (displaystyle rho_text{др}=340) кг/м(^3), плотность эфира (displaystyle rho_text{э}=720) кг/м(^3). (Ответ дайте в сантиметрах.)
Запишем условие равновесия кубика на поверхности эфира: [F_text{ Арх}=mg, quad(1)] где (F_text{ Арх}) – выталкивающая сила, действующая на брусок, (displaystyle m) – масса кубика, которую можно рассчитать, исходя из формулы (displaystyle rho_text{др}=frac {m}{V} Rightarrow m=rho_text{др} V,) где V – объем кубика, который можно вычислить по формуле [V=a^3.] Выталкивающая сила равна: [F_text{ Арх}=rho_text{э}gV_text{пчт},] где (displaystyle V_text{пчт}) – объем погруженной части кубика,[V_text{пчт}=xa^2,] где (displaystyle x) – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: [rho_text{э}gxa^2=rho_text{др}a^3] [rho_text{э}x=rho_text{др}a, text{ выразим } x=frac{rho_text{др}a}{rho_text{э}}.] Пусть (displaystyle y) – длина части стороны, находящейся над эфиром, можем записать: [y=a-x,] искомая разница длин (displaystyle delta=y-x=a-2x=a-2cdot dfrac{rho_text{др}a}{rho_text{э}}=a(1-2cdot dfrac{rho_text{др}}{rho_text{э}})) подставим в получившееся выражение численные значения: [displaystyle delta=0,18text{ м}(1-2cdot dfrac{340text{ кг}/text{м}^3}{720text{ кг}/text{м}^3})=0,01text{ м}=1text{ см}]
Ответ: 1
В некий резервуар было налито 1000 литров жидкости плотностью (displaystyle rho_1=1500) кг/м(^3). В этой жидкости в равновесии плавает кубик, погруженный в воду на (displaystyle x=130) см. Длина стороны кубика равна (displaystyle a=200) см. В сосуд доливают ещё 1000 литров жидкости плотностью (displaystyle rho_2=1100) кг/м(^3) и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)
В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. [rho_text{нов}=dfrac{rho_1+rho_2}{2}] Так как кубик плавает на поверхности, то можно записать: [mg=F_text{Арх},] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна:[F_text{Арх1}=rho_1 g V_text{пчт1},] где (displaystyle V_text{пчт1}=a^2x) – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: [F_text{Арх2}=rho_text{нов} g V_text{пчт2}=dfrac{rho_1+rho_2}{2}g V_text{пчт2},]где (displaystyle V_text{пчт2}=a^2y) – объем погруженной части куба до смешивания, (displaystyle y) – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим [rho_1 g a^2x=dfrac{rho_1+rho_2}{2} g a^2y] [rho_1x=dfrac{rho_1+rho_2}{2}y,] выразим отсюда y: [y=frac{2rho_1 x}{rho_1+rho_2},] подставим в получившееся выражение численные значения: [y=frac{2cdot1500text{ кг}/text{м}^3 cdot1,3text{ м}}{1500text{ кг}/text{м}^3+1100text{ кг}/text{м}^3}=1,5text{ м}]
Ответ: 1,5
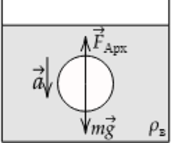
Стеклянный шарик опускается в воде с ускорением (displaystyle a=6) м/с(^2). Найти плотность стекла. Плотность воды (displaystyle rho_text{в}=1000) кг/м(^3). Силами вязкого трения пренебречь. (Ответ дайте в кг/м(^3).)
При движении шарика в воде на него действует сила тяжести (displaystyle mvec g) и сила Архимеда (displaystyle F_text{Арх}). Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: [vec F_text{Арх}+mvec g=mvec a,] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [mg- F_text{Арх}=ma,] Отсюда с учетом выражения для силы Архимеда (displaystyle F_text{Арх}=rho_text{в} g V), где V – объем шарика, а
(displaystyle rho_text{в}) – плотность воды, получим: [mg- rho_text{в} g V=ma,] Выразим массу шарика:[m=frac{rho_text{в} g V}{g-a}.] Исходя из формулы, плотность стекла равна [displaystyle rho_text{ст}=frac {m}{V}=frac{rho_text{в} g V}{(g-a)V}=frac{rho_text{в} g }{g-a},] подставим в получившееся выражение численные значения: [rho_text{ст}=frac{1000 text{ кг}/text{м}^3cdot 10text{ м}/text{с}^2 }{10text{ м}/text{с}^2-6text{ м}/text{с}^2}=2500text{ кг}/text{м}^3]
Ответ: 2500
Однородный шарик, изготовленный из материала плотностью (displaystyle rho=2000) кг/м(^3) погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
(displaystyle F_text{Арх}=100) Н? (Ответ дайте в сантиметрах и округлите до целых.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV_text{пчт},] где (displaystyle rho_text{в}) – плотность воды, (displaystyle V_text{пчт}) – объем погруженной части тела. Так как шар полностью опущен в воду, то [V_text{пчт}=frac43pi R^3,] где (displaystyle R) – радиус шара, получим: [F_text{Арх}=rho_text{в} gfrac43pi R^3, (1)] выразим из формулы R: [R=sqrt[3]{frac{3F_text{Арх}}{4rho_text{в}gpi}}] Подставив значения в формулу, получим: [R=sqrt[3]{frac{3 cdot100text{ Н}} {4 cdot1000 text{ кг}/text{м}^3cdot10text{ м}/{c^2}cdot3,14}} approx0,13text{ м}=13text{ см }]
Ответ: 13
Источник
