Сколько газа в сосуде
Random converter
- Калькуляторы
- Термодинамика — теплота
Калькулятор закона состояния идеального газа (давление–объем–температура–количество)

Калькулятор закона состояния идеального газа определяет одну из четырех величин, входящих в уравнение состояния (давление, объем, температура или количество), если известны три другие величины.
Пример: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 800 молей метана при 30 °С.
Еще несколько примеров решения задач о состоянии идеального газа под приводится калькулятором.
Выберите неизвестную величину для решения уравнения состояния идеального газа:
PVTn
Абсолютное давление
P
Объем
V
Температура
T
ИЛИ
Поделиться ссылкой на этот калькулятор, включая входные параметры
Для расчета выберите неизвестную величину и введите три известные величины из четырех имеющихся в уравнении состояния газа (давление, объем, температура, количество). Четвертая величина будет рассчитана после нажатия на кнопку Рассчитать. Количество можно ввести в молях или указать молярную массу и массу газа. Для определения молярной массы любого газа можно использовать калькулятор молярной массы. Если нужно определить молярную массу смеси газов, например, сухого воздуха, нужно определить молярные массы каждого газа и умножить их на процентное содержание по массе каждого газа в воздухе.
Примеры решения задач по уравнению состояния идеального газа (уравнению Менделеева — Клапейрона)
Задача 1: Плотность воздуха при нормальных условиях (температура 0 °С и атмосферное абсолютное давление 100 кПа) составляет 1,28 кг/м³. Определить среднюю молярную массу воздуха.
Решение: Поскольку плотность воздуха задана, это означает, что в калькулятор можно ввести массу одного кубического метра воздуха, равную 1,28 кг. Введите в калькулятор данные:
- Выберите n (Количество в молях) в селекторе Выберите неизвестную величину.
- Введите абсолютное давление P = 100 кПа.
- Введите объем V = 1 м³.
- Введите температуру T = 0 °C.
- Нажмите кнопку Рассчитать.
- Калькулятор покажет количество молей в 1 м3 воздуха.
- Введите массу воздуха m = 1,28 кг и нажмите кнопку Рассчитать.
- Калькулятор рассчитает молярную массу воздуха M = 0,029 кг/моль
Задача 2: Молярная масса газа кислорода (O₂) M = 32 г/моль. Определить абсолютную температуру 128 г. кислорода, находящегося в 10-литровом сосуде под давлением P = 3 МПа.
Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:
- Выберите T (Температура) в селекторе Выберите неизвестную величину.
- Введите молярную массу кислорода N = 32 г/моль.
- Введите массу кислорода m = 128 г.
- Калькулятор рассчитает количество кислорода в молях.
- Введите объем V = 4 л и давление P = 3 МПа.
- Нажмите кнопку Рассчитать.
- Считайте температуру в кельвинах.
Задача 3: В сосуде высокого давления находится газ под давлением P = 0.5 МПа при температуре T = 15 °С. Объем газа V = 5 л. Рассчитать объем этой массы газа при нормальных условиях (P = 100 кПа, T = 0 °С).
Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:
- Выберите T (Температура) в селекторе Выберите неизвестную величину.
- Введите давление P = 500 кПа.
- Введите температуру T = 15 °C.
- Введите объем V = 5 л.
- Нажмите кнопку Рассчитать.
- Калькулятор рассчитает количество в молях, которое будет использовано в следующем шаге.
- Выберите Объем в селекторе Выберите неизвестную величину.
- Введите температуру и давление P = 100 kPa, T = 0 °C (нормальные условия) и нажмите кнопку Рассчитать.
- Калькулятор рассчитает новый объем газа V = 23.69 л при нормальных условиях.
Задача 4: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 12,8 кг метана (молярная масса 16 г/моль) при 30 °С.
Определения и формулы
Идеальный газ
Идеальный газ — теоретическая модель, в которой газ представляется в виде множества свободно движущихся частиц бесконечно малого размера, которые взаимодействуют друг с другом абсолютно упруго, то есть при столкновении двух частиц их кинетическая энергия не изменяется и не превращается ни в какую другую форму энергию, например, в потенциальную энергию или в тепло. Считается, что суммарный размер частиц настолько мал, что занимаемый ими объем в сосуде пренебрежимо мал. Эта теоретическая модель полезна, так как она упрощает многие расчеты, а также в связи с тем, что идеальный газ подчиняется законам классической механики. Идеальный газ можно представить себе в виде множества абсолютно твердых сфер, которые только сталкиваются друг с другом и больше никак не взаимодействуют.
В обычных условиях, например, при стандартных условиях (при температуре 273,15 К и давлении в 1 стандартную атмосферу) большинство реальных газов ведут себя как идеальный газ. В общем случае, газ ведет себя как идеальный при низком давлении и высокой температуре, когда расстояния между молекулами газа относительно велики. В этих условиях потенциальная энергия вследствие действия межмолекулярных сил намного меньше кинетической энергии частиц. Размер молекул также незначителен по сравнению с расстоянием между ними. Идеальная модель не работает при низких температурах и высоких давлениях, а также для тяжелых газов. При понижении температуры и повышении давления реальный газ может стать жидкостью или даже перейти в твердое состояние, то есть может произойти фазовый переход. В то же время, модель идеального газа не допускает жидкого или твердого состояния.
Закон идеального газа
Идеальный газ, как и любой другой газ, можно охарактеризовать четырьмя переменными и одной константой, а именно:
- давление (P),
- объем (V),
- количество в молях (n),
- температура (T), and
- универсальная газовая постоянная (R)
Эти четыре переменные и одна константа объединены в приведенном ниже уравнении, которое называется уравнением состояния идеального газа:
Это уравнение также известно под названием закона идеального газа и уравнения Менделеева — Клапейрона или уравнения Клапейрона, так как уравнение было впервые выведено в 1834 г. французским инженером Эмилем Клапейроном (1799–1864). О вкладе Д. И. Менделеева — чуть ниже. В этом уравнении:
- P — абсолютное давление, измеряемое в СИ в паскалях (Па),
- V — объем, измеряемый в СИ в кубических метрах (м³),
- n — количество вещества (газа) в молях (сокращение моль). Один моль любого вещества в граммах численно равен средней массы одной молекулы в соединении, выраженной в атомных единицах массы. Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.
- T — абсолютная температура.
- R — универсальная газовая постоянная, являющаяся физическим коэффициентом пропорциональности уравнения состояния идеального газа.
Приведенное выше уравнение показывает, что при нулевой абсолютной температуре получается нулевой объем. Однако это не означает, что объем реального газа действительно исчезает. При очень низких температурах все газы становятся жидкостями и уравнение идеального газа к ним неприменимо.
Универсальная газовая постоянная соответствует работе, выполненной при расширении одного моля идеального газа при нагревании на 1 К при постоянном давлении. Размерность постоянной — работа на количество вещества на температуру. Постоянная в точности равна 8,31446261815324 Дж⋅К⁻¹⋅моль⁻¹. Универсальная газовая постоянная также определяется как произведение числа Авогадро NA и постоянной Больцмана k:
Входящая в уравнение состояния идеального газа универсальная газовая постоянная была предложена и введена в уравнение Дмитрием Менделеевым в 1877 г. Поэтому уравнение состояния идеального газа в литературе на русском языке и ее переводах на другие языки, называется уравнением Менделеева — Клапейрона.
Количество газа в молях часто бывает удобно заменить массой газа. Количество газа в молях n, его масса m в граммах и молярная масса M в граммах на моль связаны формулой:
Заменяя в уравнении состояния идеального газа n на m/M, имеем:
Для определения молярной массы элемента, его относительная атомная масса умножается на коэффициент молярной массы в кг/моль
Например, молярная масса кислорода в единицах системы СИ
Если ввести в уравнение состояния идеального газа плотность ρ = m/V, мы получим:
Теперь введем понятие удельной газовой постоянной, которая представляет собой отношение универсальной газовой постоянной R к молярной массе M:
Например, удельная газовая постоянная сухого воздуха приблизительно равна 287 Дж·кг⁻¹·К⁻¹. Подставив удельную газовую постоянную в уравнение состояния идеального газа, получим:
Закон идеального газа объединяет четыре более простых эмпирических газовых закона, открытых в XVII–XIX вв. несколькими учеными, которые аккуратно измеряли свойства газа. Простые газовые законы можно также вывести из уравнения состояния идеального газа (PV=nRT). Поскольку в этом уравнении R является постоянной величиной, можно записать
Поскольку PV/NT — постоянная величина, можно записать это иначе:
Здесь индексы 1 и 2 показывают начальное и конечное состояние газа в системе. Мы будем использовать это уравнение ниже при описании четырех газовых законов.
Отметим, что исторически именно эмпирические законы поведения газа, описанные ниже, привели к открытию обобщенного закона состояния идеального газа. Эти законы были открыты несколькими учеными, которые проводили эксперименты, изменяя только две переменные состояния газа и оставляя две другие переменные постоянными.
Закон Бойля — Мариотта (T=const, n=const)
Роберт Бойль
Изменим предыдущее уравнение с учетом, что количество газа в молях n и его температура Т остаются неизменными:
или
Эдм Мариотт
Это закон Бойля — Мариотта, описывающий зависимость объема V фиксированного количества газа в молях n от давления P при постоянной температуре T. Давление фиксированной массы газа при неизменной температуре обратно пропорционально его объему. Закон был сформулирован англо-ирландским химиком и физиком Робертом Бойлем в 1662 г. В России и континентальной Европе это закон называют законом Бойля — Мариотта с учетом вклада в открытие закона французского физика и священника Эдма Мариотта.
Закон Авогадро (T=const, P=const)
Амедео Авогадро
Если температура и давление остаются неизменными, можно записать
Это закон Авогадро, указывающий, что при неизменных температуре и давлении равные объемы любых газов содержат одинаковое количество молекул. Это уравнение показывает, что, если количество газа увеличивается, объем газа пропорционально растет. Иными словами, количество атомов или молекул газа не зависит от их размеров или от молярной массы газа. Закон назван в честь итальянского ученого Амедео Авогадро, который опубликовал гипотезу об отношениях объема газа и его количества в молях в 1811 году. Число Авогадро также носит его имя.
Закон Гей-Люссака (P=const, n=const)
Жак Шарль
При постоянном давлении объем фиксированного количества газа в молях пропорционален абсолютной температуре системы с газом.
В англоязычной литературе этот закон называется законом объемов и законом Шарля. Закон описывает как расширяется любой газ при увеличении его абсолютной температуры. Закон был сформулирован в неопубликованной работе французским ученым Жаком Шарлем в 80-х гг. XVIII в. Его соотечественник Жозеф Луи Гей-Люссак опубликовал этот закон в 1803 г. и указал, что приоритет открытия принадлежит Жаку Шарлю. Поэтому этот закон в литературе не на английском языке часто называют законом Гей-Люссака. В русскоязычной литературе закон носит имя Гей-Люссака. Итальянцы называют этот закон первым законом Гей-Люссака (ит. prima legge di Gay-Lussac).
Закон Шарля (или второй закон Гей-Люссака) (V=const, n=const)
Жозеф Луи Гей-Люссак
Закон Шарля (называемый также вторым законом Гей-Люссака) гласит, что давление фиксированного количества газа в молях при его неизменном объеме прямо пропорционально абсолютной температуре газа:
Закон был сформулирован Гей-Люссаком в 1802 г. В литературе на других языках этот закон также называют законом Амонтона по имени французского ученого Гийома Амонтона, который на сто лет раньше обнаружил количественную зависимость объема газа от его температуры. Иногда закон называют вторым законом Гей-Люссака и законом Шарля, так как сам Гей-Люссак считал, что закон открыт Шарлем. Закон зависимости давления от температуры был также независимо открыт английским физиком Джоном Дальтоном в 1801 г. Итальянцы называют этот закон вторым законом Вольта–Гей-Люссака (ит. seconda legge di Volta – Gay-Lussac), потому что итальянец Алессандро Вольта независимо проводил исследования газов и получил аналогичные результаты.
При нагревании воздуха в оболочке воздушного шара его плотность уменьшается и становится меньше плотности окружающего воздуха; в результате шар приобретает положительную плавучесть
Источник
8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В сосуде объёмом 2 л находится 10 г идеального газа при давлении 1 атм. и температуре 300 К. Во втором сосуде объёмом 4 л находится 20 г того же газа при давлении 2 атм. Чему равна температура газа во втором сосуде? (Ответ дайте в кельвинах.)
Уравнение состояния газа: [pV=nu RT=dfrac{m}{mu}RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества, (R) — универсальная газовая постоянная, (T) — температура газа, (m) — масса газа, (mu) — молярная масса газа.
Для первого сосуда: [p_1V_1=dfrac{m_1}{mu}RT_1] Для второго сосуда: [p_2V_2=dfrac{m_2}{mu}RT_2] Поделим уравнения друг на друга: [dfrac{p_1V_1}{p_2V_2}=frac{m_1T_1}{m_2T_2}] [T_2=T_1cdotdfrac{m_1}{m_2}cdotdfrac{V_2}{V_1}cdotdfrac{p_2}{p_1}=300text{ К}cdotdfrac{1}{2}cdot2cdot2=600 text{ К}]
Ответ: 600
При уменьшении абсолютной температуры газа на 300 К давление уменьшилось в 5 раз. Какова начальная температура газа, если в ходе эксперимента количество вещества уменьшилось втрое, а объём оставался постоянным? (Ответ дайте в кельвинах.)
Запишем уравнение Менделеева-Клапейрона для первого и второго состояния: [begin{cases}
p_1 V=nu_1 R T_1\
p_2 V=nu_2 R T_2
end{cases}] где (p_1) и (p_2) — давления газа в первом и втором состояниях, V — объём газа, (nu_1) и (nu_2)— количество вещества в первом и втором состояниях, (R) — универсальная газовая постоянная, (T_1) и (T_2) — абсолютная температура в первом и втором состояниях.
Поделив одно уравнение на другое, получим: [dfrac{p_1}{p_2} = dfrac{nu_1 T_1}{nu_2 T_2}] Так как (nu_1 = 3nu_2) и (p_1 = 5p_2), то: [dfrac{5p_2}{p_2} = dfrac{3nu_2cdot T_1}{nu_2cdot T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5=dfrac{3T_1}{T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_2 = 3T_1] Так как (T_2 = (T_1 – 200) К), то: [5(T_1 – 300text{ K}) = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_1 – 1500text{ K } = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
2T_1 = 1500text{ K }
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
T_1 = 750text{ K }]
Ответ: 750
На графиках приведены зависимости давления (p) и объема (V) от времени (t) для 1 моля идеального газа. Чему равна температура газа в момент (t) = 30 минут? (Ответ дайте в градусах Кельвина с точностью до 10 К.)
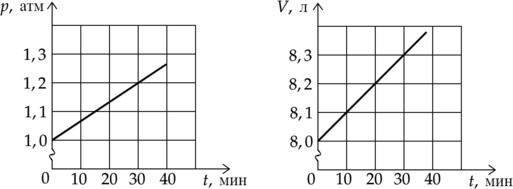
Уравнение состояния идеального газа: [displaystyle pV=nu RT,] где (p)—давление газа, (V)—объем газа, (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (T) — температура. Выразим температуру газа: [T=dfrac{pV}{nu R}] Из графика найдем давление и объем в момент времени 30 мин:
(p=1,2cdot10^5) Па
(V=8,3cdot10^{-3}text{ м$^3$})
Подставим известные и найденные значения в формулу: [T=dfrac{1,2cdot10^5text{ Па}cdot8,3cdot10^{-3}text{ м$^3$}}{1text{ моль}cdot8,31text{ }dfrac{text{Дж}}{text{моль}}} approx 120 text{ К}]
Ответ: 120
В сосуде неизменного объёма находится разреженный газ в количестве 3 моль. Во сколько раз изменится давление газа в сосуде, если выпустить из него 1 моль газа, а абсолютную температуру газа уменьшить в 2 раза?
“Демоверсия 2019”
Запишем уравнение Клапейрона – Менделеева: [p1V=nu_1RT_1=3RT_1] [p_2V=nu_2RT_2=2Rdfrac{T_1}{2}=RT_1] [dfrac{p_1}{p_2}=dfrac{3RT_1}{RT_1}=3]
Ответ: 3
В сосуде неизменного объёма находится идеальный газ. Во сколько раз нужно увеличить количество газа в сосуде, чтобы после уменьшения абсолютной температуры газа в 2 раза его давление стало вдвое больше начального?
“Досрочная волна 2020 вариант 1”
Из уравнения Клапейрона –Менделеева: [pV=nu RT] чтобы давление ((p)) увеличилось в 2 раза, при уменьшении температуры ((T)) в 2 раза, количество вещества ((nu)) должно увеличится в 4 раза
Ответ: 4
В сосуде неизменного объема находится разреженный газ в количестве 4 моль. Во сколько раз нужно увеличить абсолютную температуру газа, чтобы после удаления из сосуда 3 моль газа, давление осталось неизменным?
“Основная волна 2020 ”
Уравнение Клайперона – Менделеева: [pV=nu RT] если удалить 3 моль газа, то количество вещества уменьшится в 4 раза (nu_1=dfrac{nu}{4}), следовательно, температуру надо увеличить в 4 раза.
Ответ: 4
Источник
5.4. Практическое применение уравнения состояния идеального газа
5.4.2. Уравнение состояния для газа в закрытом сосуде
При рассмотрении идеального газа, находящегося в закрытом сосуде (баллоне), необходимо учитывать, что изменение термодинамических параметров происходит при постоянной массе газа.
Для идеального газа, находящегося в закрытом сосуде, необходимо учитывать следующее:
- масса газа, находящегося в закрытом сосуде, вследствие изменения его термодинамических параметров не изменяется:
m = const;
- объем газа, заполняющего сосуд определенного объема, также фиксирован: V = const;
- постоянными также остаются следующие параметры газа:
ρ = const; ν = const; n = const;
где ρ — плотность газа; ν — количество вещества (газа); n — концентрация молекул (атомов) газа.
Для идеального газа, находящегося в закрытом сосуде и изменяющего свое состояние, уравнение Менделеева — Клапейрона записывается в виде системы (рис. 5.8):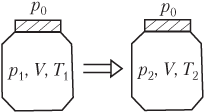
p1V=νRT1,p2V=νRT2,}
где p
1, T
1 — давление и температура газа в начальном состоянии; p
2, T
2 — давление и температура газа в конечном состоянии; V — объем баллона; ν — количество газа; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Термин избыточное давление, встречающийся в задачах об идеальном газе в закрытом сосуде (баллоне), означает абсолютную разность между давлением газа, находящегося в сосуде, и давлением на стенки сосуда снаружи:
p
изб = |p − p
0|,
где p — давление газа, находящегося внутри сосуда; p
0 — давление (атмосферное либо гидростатическое) на стенки сосуда снаружи.
Пример 13. Баллон рассчитан на максимальное избыточное давление 150 МПа. В него накачали газ при температуре 300 К до давления 120 МПа. Постепенно нагревая газ, баллон погружают в воду плотностью 1000 кг/м3 на глубину 1000 м. До какой максимальной температуры можно нагреть газ в баллоне, чтобы он не взорвался?
Решение. Запишем уравнение Менделеева — Клапейрона для двух состояний газа, находящегося в баллоне:
- в начале нагревания
p
1V = νRT
1;
- в конце нагревания
p
2V = νRT
2;
где p
1 — первоначальное давление газа в баллоне; p
2 — давление газа в баллоне в конце нагревания; V — объем газа (баллона), V = const; ν — количество вещества (газа) в баллоне; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в начале процесса; T
2 — температура газа в конце процесса.
Отношение уравнений
p1Vp2V=νRT1νRT2
позволяет определить давление газа в конце процесса:
p2=p1T2T1.
В условии задачи задано максимальное избыточное давление, определяемое формулой
pизбmax=|p2−p0|,
где p
0 — давление снаружи баллона; p
2 — давление газа внутри баллона.
При погружении баллона в воду с одновременным нагреванием указанные давления снаружи и внутри баллона определяются следующими формулами:
- снаружи (сумма атмосферного и гидростатического давлений) —
p
0 = p
атм + p
гидр = p
атм + ρ0gh,
где p
атм — атмосферное давление; p
гидр — гидростатическое давление, p
гидр = ρ0gh; ρ0 — плотность воды; g — модуль ускорения свободного падения; h — глубина погружения баллона;
- внутри (давление газа) —
p2=p1T2T1,
где T
2 — максимальная температура газа (искомая величина).
Подстановка выражений для давлений внутри и снаружи баллона в формулу для избыточного давления дает
pизбmax=|p1T2T1−ρ0gh−pатм|≈|p1T2T1−ρ0gh|,
так как p
атм << ρ0gh, p
атм << p
2.
Данное уравнение содержит модуль разности, что приводит к двум независимым уравнениям:
pизбmax=p1T2T1−ρ0gh, pизбmax=ρ0gh−p1T2T1,
из которых следуют две формулы для расчета искомой величины:
T2=T1⋅ρ0gh+pизбmaxp1, T2=T1⋅ρ0gh−pизбmaxp1.
Максимальному значению искомой температуры соответствует значение, рассчитанное по первой формуле:
T2=300⋅1000⋅10⋅1000+150⋅106120⋅106=400 К.
Чтобы баллон не взорвался, его можно погрузить на заданную глубину, одновременно нагревая до температуры 400 К.
Пример 14. Бутылка емкостью 0,75 л выдерживает максимальное избыточное давление 150 кПа. Из бутылки откачивают воздух и запечатывают некоторое количество твердого углекислого газа с молярной массой 44,0 г/моль. Атмосферное давление равно 100 кПа. Считая, что объем твердого углекислого газа пренебрежимо мал по сравнению с объемом бутылки, найти его максимальную массу, которая не вызовет взрыва бутылки при температуре 300 К?
Решение. Запишем уравнение Менделеева — Клапейрона для углекислого газа, находящегося в бутылке, после его превращения в газообразное состояние:
pV=mMRT,
где p — давление углекислого газа в бутылке; V — объем газа (бутылки); m — масса углекислого газа в бутылке; M — молярная масса углекислого газа; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа.
Записанное уравнение позволяет получить выражение для расчета давления газа внутри бутылки:
p=mRTVM.
В условии задачи задано максимальное избыточное давление, определяемое формулой
pизбmax=|p−p0|,
где p
0 — давление снаружи бутылки.
Указанные давления снаружи и внутри бутылки определяются следующим образом:
- снаружи (атмосферное давление) — p
0; - внутри (давление углекислого газа) —
p=mRTVM,
где m соответствует искомой величине — максимальной массе углекислого газа.
Подстановка выражений для давлений внутри и снаружи баллона в формулу для избыточного давления дает
pизбmax=|mRTVM−p0|.
Данное уравнение содержит модуль разности, что приводит к двум независимым уравнениям:
pизбmax=mRTVM−p0, pизбmax=p0−mRTVM,
из которых следуют две формулы для расчета искомой величины:
m=VM(p0+pизбmax)RT, m=VM(p0−pизбmax)RT.
Максимальному значению искомой массы соответствует значение, рассчитанное по первой формуле:
m=0,75⋅10−3⋅44,0⋅10−3(100+150)⋅1038,31⋅300=3,3⋅10−3 кг=3,3 г.
Чтобы бутылка не взорвалась, в нее можно запечатать не более 3,3 г твердого углекислого газа.
Пример 15. В наличии имеется неограниченное количество баллонов объемом по 4,0 л, заполненных некоторым идеальным газом до давления 500 кПа. Баллоны предназначены для наполнения газом оболочки аэрозонда и их можно соединять между собой. Сколько баллонов с газом необходимо одновременно подсоединить к пустой оболочке аэрозонда объемом 800 дм3, чтобы наполнить ее до давления 100 кПа, равного атмосферному? Температура газа при заполнении оболочки не изменяется.
Решение. Для осуществления процесса, описанного в условии задачи, требуется определенное количество газа ν.
Необходимое количество газа заполняет следующий объем:
- в начале процесса (до заполнения оболочки)
V
1 = NV
бал,
где N — количество баллонов; V
бал — объем одного баллона, V
бал = 4,0 л;
- в конце процесса (после заполнения оболочки)
V
2 = NV
бал + V
обол,
где V
обол — объем оболочки, V
обол = 800 дм3.
Указанное количество газа находится при давлении:
- в начале процесса (до заполнения оболочки) —
p
1 = 500 кПа
и совпадает с давлением газа в каждом из баллонов;
- в конце процесса (после заполнения оболочки) —
p
2 = 100 кПа
и совпадает с давлением в оболочке.
Считая процесс заполнения газом оболочки аэрозонда изотермическим, запишем уравнение Менделеева — Клапейрона следующим образом:
- в начале процесса (до заполнения оболочки) —
p
1V
1 = νRT,
где ν — количество вещества (газа) в оболочке; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- в конце процесса (после заполнения оболочки) —
p
2V
2 = νRT.
Равенство
p
1V
1 = p
2V
2,
записанное в явном виде
p
1NV
бал = p
2(NV
бал + V
обол),
позволяет получить формулу для вычисления искомого числа баллонов:
N=VоболVбал⋅p2p1−p2.
Произведем расчет:
N=800⋅10−34,0⋅10−3⋅100⋅103(500−100)⋅103=50.
Следовательно, для заполнения оболочки до указанного давления необходимо 50 баллонов с газом.
Пример 16. Аэростат, оболочка которого заполнена азотом с молярной массой 28 г/моль, находится в воздухе. Молярная масса воздуха равна 29 г/моль. Массы гондолы и оболочки аэростата пренебрежимо малы. Во сколько раз возрастет подъемная сила аэростата, если азот в его оболочке заменить на водород с молярной массой 2,0 г/моль, не изменяя при этом объем аэростата?
Решение. Силы (сила тяжести mg→ и сила Архимеда F→A), действующие на аэростат, показаны на рисунке.
Подъемная сила — это векторная сумма силы тяжести и силы Архимеда:
F→под=F→A+mg→,
где F→A — сила Архимеда, действующая на оболочку со стороны воздуха; mg→ — сила тяжести; m — масса газа, заполняющего оболочку аэростата; g→ — ускорение свободного падения.
В проекциях на вертикальную ось подъемная сила определяется следующими выражениями:
- при заполнении оболочки азотом —
F
под1 = F
A1 − m
1g,
где F
A1 — модуль силы Архимеда, действующей на оболочку аэростата при заполнении оболочки азотом, F
A1 = ρ0gV
1; ρ0 — плотность воздуха; V
1 — объем оболочки аэростата при заполнении ее азотом (объем воздуха, вытесненного оболочкой); m
1 — масса азота, заполняющего оболочку, m
1 = ρ1V
1; ρ1 — плотность азота;
- при заполнении оболочки водородом —
F
под2 = F
A2 − m
2g,
где F
A2 — модуль силы Архимеда, действующей на оболочку аэростата при заполнении оболочки водородом, F
A2 = ρ0gV
2; V
2 — объем оболочки аэростата при заполнении ее водородом (объем воздуха, вытесненного оболочкой); m
2 — масса водорода, заполняющего оболочку, m
2 = ρ2V
2; ρ2 — плотность водорода.
Искомой величиной является отношение
Fпод2Fпод1=FA2−m2gFA1−m1g.
С учетом записанных выражений для сил Архимеда, масс азота и водорода, а также равенства объемов оболочки при заполнении ее азотом и водородом (V
1 = V
2), указанное отношение принимает вид
Fпод2Fпод1=ρ0gV2−ρ2V2gρ0gV1−ρ1V1g=(ρ0−ρ2)V2g(ρ0−ρ1)V1g=ρ0−ρ2ρ0−ρ1.
Плотности воздуха, азота и водорода определим как отношения:
- для воздуха
ρ0=M0Vμ0,
где M
0 — молярная масса воздуха; V
µ0 — молярный объем воздуха;
- для азота
ρ1=M1Vμ1,
где M
1 — молярная масса азота; V
µ1 — молярный объем азота;
- для водорода
ρ2=M2Vμ2,
где M
2 — молярная масса водорода; V
µ2 — молярный объем водорода.
Молярные объемы (объемы одного моля) воздуха, азота и водорода равны между собой, так как газы находятся при одних и тех же условиях:
V
µ0 = V
µ1 = V
µ2 = V
µ.
Поэтому формула для расчета искомого отношения приобретает вид
Fпод2Fпод1=ρ0−ρ2ρ0−ρ1=M0−M2M0−M1.
Расчет дает значение:
Fпод2Fпод1=29⋅10−3−2,0⋅10−329⋅10−3−28⋅10−3=27.
При замене азота на водород в оболочке аэростата его подъемная сила возрастет в 27 раз.
Пример 17. Воздушный шар с температурой 300 К находится в воздухе при атмосферном давлении 100 кПа. Молярная масса воздуха составляет 29,0 г/моль. Объем воздушного шара равен 830 дм3, а масса его оболочки равна 333 г. На сколько градусов необходимо нагреть газ в оболочке, чтобы шар взлетел? Воздух в оболочке шара сообщается с атмосферой.
Решение. Силы, действующие на воздушный шар, показаны на рисунке:
- сила Архимеда
F
A = ρ0gV,
где ρ0 — плотность воздуха, окружающего шар; g — модуль ускорения свободного падения; V — объем оболочки шара (объем вытесненного оболочкой воздуха);
- сила тяжести
mg = (m
обол + m
возд)g,
где m
обол — масса оболочки; m
возд — масса воздуха в оболочке, m
возд = ρV; ρ — плотность воздуха внутри оболочки.
Шар взлетает, когда выполняется равенство
F→A+mg→=0,
или, в проекции на вертикальную ось, —
F
A − mg = 0.
Преобразуем равенство (условие равновесия шара в воздухе)
F
A = mg
с учетом записанных выше выражений
ρ0gV = (m
обол + m
возд)g, или (ρ0 − ρ)V = m
обол.
Входящие в равенство плотности воздуха не известны, но фигурируют в качестве параметра в уравнении состояния:
- для воздуха снаружи оболочки воздушного шара
p0=ρ0RT1M,
где p
0 — атмосферное давление; ρ0 — плотность воздуха снаружи оболочки; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура окружающего шар воздуха; M — молярная масса воздуха;
- для воздуха внутри оболочки воздушного шара
p=ρRT2M,
где p — давление воздуха внутри оболочки; ρ — плотность воздуха внутри оболочки; T
2 — температура воздуха внутри оболочки.
Давления воздуха внутри и снаружи оболочки воздушного шара одинаковы, так как воздух, находящийся в оболочке, сообщается с атмосферой; поэтому
p = p
0.
Плотности:
- для воздуха снаружи оболочки воздушного шара
ρ0=p0MRT1;
- для воздуха внутри оболочки воздушного шара
ρ=p0MRT2.
Подставим выражения для плотностей в условие равновесия шара в воздухе:
(1T1−1T2)p0MVR=mобол.
Температура воздуха внутри оболочки, при которой шар начинает взлетать, определяется как
T2=p0MVT1p0MV−RT1mобол,
а искомая разность —
ΔT=T2−T1=p0MVT1p0MV−RT1mобол−T1=T1p0MVRT1mобол−1.
Произведем вычисление:
ΔT=300100⋅103⋅29,0⋅10−3⋅830⋅10−38,31⋅300⋅333⋅10−3−1=158 К.
Следовательно, чтобы воздушный шар начал взлетать, воздух в его оболочке необходимо нагреть на 158 К, или 158 °С.
Пример 18. Камеру футбольного мяча объемом 3,00 л накачивают с помощью насоса, забирающего из атмосферы 0,150 л воздуха при каждом качании. Атмосферное давление составляет 100 кПа. Определить давление в камере после 30 качаний, если первоначально она была пустой. Температура постоянна.
Решение. За N качаний насос забирает из атмосферы определенное количество воздуха ν. Это же количество воздуха попадает в камеру футбольного мяча.
Указанное количество воздуха имеет следующий объем:
- воздух, забранный из атмосферы за N качаний насоса, —
V
1 = NV
нас,
где V
нас — объем насоса, V
нас = 0,150 л; N — количество качаний;
- воздух, накачанный в камеру футбольного мяча, —
V
2 = V
мяч,
где V
мяч — объем камеры мяча, V
мяч = 3,00 л.
Данное количество воздуха находится при следующем давлении:
- воздух, забранный из атмосферы за N качаний насоса, —
p
1 = 100 кПа
совпадает с атмосферным давлением;
