Сколько молей идеального газа находится в сосуде
8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В сосуде объёмом 2 л находится 10 г идеального газа при давлении 1 атм. и температуре 300 К. Во втором сосуде объёмом 4 л находится 20 г того же газа при давлении 2 атм. Чему равна температура газа во втором сосуде? (Ответ дайте в кельвинах.)
Уравнение состояния газа: [pV=nu RT=dfrac{m}{mu}RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества, (R) — универсальная газовая постоянная, (T) — температура газа, (m) — масса газа, (mu) — молярная масса газа.
Для первого сосуда: [p_1V_1=dfrac{m_1}{mu}RT_1] Для второго сосуда: [p_2V_2=dfrac{m_2}{mu}RT_2] Поделим уравнения друг на друга: [dfrac{p_1V_1}{p_2V_2}=frac{m_1T_1}{m_2T_2}] [T_2=T_1cdotdfrac{m_1}{m_2}cdotdfrac{V_2}{V_1}cdotdfrac{p_2}{p_1}=300text{ К}cdotdfrac{1}{2}cdot2cdot2=600 text{ К}]
Ответ: 600
При уменьшении абсолютной температуры газа на 300 К давление уменьшилось в 5 раз. Какова начальная температура газа, если в ходе эксперимента количество вещества уменьшилось втрое, а объём оставался постоянным? (Ответ дайте в кельвинах.)
Запишем уравнение Менделеева-Клапейрона для первого и второго состояния: [begin{cases}
p_1 V=nu_1 R T_1\
p_2 V=nu_2 R T_2
end{cases}] где (p_1) и (p_2) — давления газа в первом и втором состояниях, V — объём газа, (nu_1) и (nu_2)— количество вещества в первом и втором состояниях, (R) — универсальная газовая постоянная, (T_1) и (T_2) — абсолютная температура в первом и втором состояниях.
Поделив одно уравнение на другое, получим: [dfrac{p_1}{p_2} = dfrac{nu_1 T_1}{nu_2 T_2}] Так как (nu_1 = 3nu_2) и (p_1 = 5p_2), то: [dfrac{5p_2}{p_2} = dfrac{3nu_2cdot T_1}{nu_2cdot T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5=dfrac{3T_1}{T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_2 = 3T_1] Так как (T_2 = (T_1 – 200) К), то: [5(T_1 – 300text{ K}) = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_1 – 1500text{ K } = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
2T_1 = 1500text{ K }
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
T_1 = 750text{ K }]
Ответ: 750
На графиках приведены зависимости давления (p) и объема (V) от времени (t) для 1 моля идеального газа. Чему равна температура газа в момент (t) = 30 минут? (Ответ дайте в градусах Кельвина с точностью до 10 К.)
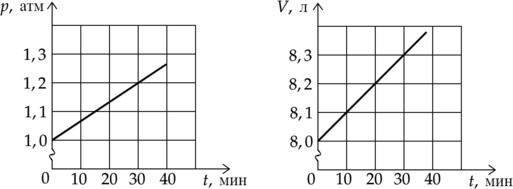
Уравнение состояния идеального газа: [displaystyle pV=nu RT,] где (p)—давление газа, (V)—объем газа, (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (T) — температура. Выразим температуру газа: [T=dfrac{pV}{nu R}] Из графика найдем давление и объем в момент времени 30 мин:
(p=1,2cdot10^5) Па
(V=8,3cdot10^{-3}text{ м$^3$})
Подставим известные и найденные значения в формулу: [T=dfrac{1,2cdot10^5text{ Па}cdot8,3cdot10^{-3}text{ м$^3$}}{1text{ моль}cdot8,31text{ }dfrac{text{Дж}}{text{моль}}} approx 120 text{ К}]
Ответ: 120
В сосуде неизменного объёма находится разреженный газ в количестве 3 моль. Во сколько раз изменится давление газа в сосуде, если выпустить из него 1 моль газа, а абсолютную температуру газа уменьшить в 2 раза?
“Демоверсия 2019”
Запишем уравнение Клапейрона – Менделеева: [p1V=nu_1RT_1=3RT_1] [p_2V=nu_2RT_2=2Rdfrac{T_1}{2}=RT_1] [dfrac{p_1}{p_2}=dfrac{3RT_1}{RT_1}=3]
Ответ: 3
В сосуде неизменного объёма находится идеальный газ. Во сколько раз нужно увеличить количество газа в сосуде, чтобы после уменьшения абсолютной температуры газа в 2 раза его давление стало вдвое больше начального?
“Досрочная волна 2020 вариант 1”
Из уравнения Клапейрона –Менделеева: [pV=nu RT] чтобы давление ((p)) увеличилось в 2 раза, при уменьшении температуры ((T)) в 2 раза, количество вещества ((nu)) должно увеличится в 4 раза
Ответ: 4
В сосуде неизменного объема находится разреженный газ в количестве 4 моль. Во сколько раз нужно увеличить абсолютную температуру газа, чтобы после удаления из сосуда 3 моль газа, давление осталось неизменным?
“Основная волна 2020 ”
Уравнение Клайперона – Менделеева: [pV=nu RT] если удалить 3 моль газа, то количество вещества уменьшится в 4 раза (nu_1=dfrac{nu}{4}), следовательно, температуру надо увеличить в 4 раза.
Ответ: 4
Источник
5.4. Практическое применение уравнения состояния идеального газа
5.4.1. Уравнение состояния для идеального газа в открытом сосуде
При рассмотрении идеального газа, находящегося в открытом сосуде, необходимо учитывать, что вследствие изменения термодинамических параметров часть газа выходит из сосуда. При этом уравнение состояния записывается только для той части газа, которая остается в сосуде.
Для идеального газа, находящегося в открытом сосуде, необходимо учитывать следующее:
- масса газа изменяется в результате изменения его термодинамических параметров:
m ≠ const;
- рассматривается газ, оставшийся в сосуде определенного объема, т.е. объем газа фиксирован:
V = const;
- давление газа может изменяться или оставаться постоянным (в зависимости от условия задачи), причем на изменение давления в условии задачи обычно бывает четкое указание.
Если давление идеального газа в открытом сосуде по условию задачи изменяется (p ≠ const), то уравнение Менделеева — Клапейрона записывается для двух состояний газа в виде системы (рис. 5.7):Рис. 5.7
p1V=m1MRT1,p2V=m2MRT2,}
где p
1, m
1, T
1 — давление, масса и температура газа в начальном состоянии; p
2, m
2, T
2 — указанные параметры газа в конечном состоянии; V — объем сосуда; M — молярная масса газа; R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К).
Если давление идеального газа в открытом сосуде по условию задачи остается постоянным (p = const), то изменения некоторых характеристик газа в открытом сосуде можно вычислить по следующим формулам:
- изменение массы
Δm=m1−m2=m1(1−T1T2),
где m
1 — первоначальная масса газа; m
2 — масса газа в конце процесса; T
1 — термодинамическая (абсолютная) температура газа в начале процесса; T
2 — термодинамическая (абсолютная) температура газа в конце процесса;
- изменение плотности
Δρ=ρ1−ρ2=ρ1(1−T1T2),
где ρ1 — первоначальная плотность газа; ρ2 — плотность газа в конце процесса;
- изменение количества вещества
Δν=ν1−ν2=ν1(1−T1T2),
где ν1 — первоначальное количество вещества (газа) в сосуде; ν2 — количество вещества (газа) в сосуде в конце процесса.
Пример 11. В открытом сосуде объемом 450 дм3 содержится некоторое количество идеального газа. Температуру газа увеличивают от 27 до 177 °С. Давление газа остается постоянным и равным 166 кПа. Сколько моль газа выйдет из сосуда?
Решение. Запишем уравнение Менделеева — Клапейрона для двух состояний газа, находящегося в открытом сосуде, при нагревании:
- для начального состояния
pV = ν1RT
1;
- для конечного состояния
pV = ν2RT
2;
где p — давление газа, p = const; V — объем газа (сосуда), V = const; ν1, ν2 — количество вещества (газа) в начале и в конце процесса; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1, T
2 — температура газа в начале и в конце процесса.
Первое уравнение позволяет получить формулу для расчета количества вещества (газа) в начале процесса:
ν1=pVRT1.
Подстановка полученной формулы в уравнение
Δν=ν1(1−T1T2)
дает искомую разность
Δν=pVRT1(1−T1T2)=pV(T2−T1)RT1T2.
Для вычисления искомой величины необходимо перевести температуру из градусов Цельсия в кельвины:
T
1 = t
1 + 273 = 27 + 273 = 300 К,
T
2 = t
2 + 273 = 177 + 273 = 450 К.
Произведем вычисление:
Δν=166⋅103⋅450⋅10−3(450−300)8,31⋅450⋅300=10 моль.
При нагревании из сосуда вышло 10 моль газа.
Пример 12. В баллоне при температуре 15 °С находится идеальный газ. Из баллона выходит 40 % газа, а температура при этом понижается на 8,0 °С. Во сколько раз уменьшится давление газа в баллоне?
Решение. Запишем уравнение Менделеева — Клапейрона для двух состояний газа, находящегося в открытом сосуде:
- для начального состояния
p
1V = ν1RT
1;
- для конечного состояния
p
2V = ν2RT
2;
где p
1 — давление газа в начальном состоянии; p
2 — давление газа в конечном состоянии; V — объем газа (сосуда), V = const; ν1, ν2 — количество вещества (газа) в начале и в конце процесса соответственно; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1, T
2 — температура газа в начале и в конце процесса соответственно.
Искомой величиной является отношение давлений p
1/p
2, которое определим из отношения уравнений:
p1Vp2V=ν1RT1ν2RT2, т.е. p1p2=ν1T1ν2T2.
В результате процесса из баллона выходит 40 % газа, поэтому количество вещества (газа) ν2, оставшегося в баллоне, составляет 60 % от количества вещества (газа) ν1, которое было в начале процесса:
ν2 = 0,6ν1.
Для вычисления искомой величины необходимо сделать перевод температуры, заданной в градусах Цельсия, в кельвины:
T
1 = t
1 + 273 = 15 + 273 = 288 К,
T
2 = t
2 + 273 = (t
1 − Δt) + 273 = (15 − 8,0) + 273 = 280 К.
Подстановка температур и количества вещества (газа), оставшегося в баллоне, в выражение для искомой величины дает
p1p2=ν1T10,6ν1T2=T10,6T2=2880,6⋅280=1,7.
Давление газа в баллоне понизится в 1,7 раза.
Источник
2011 год 109 вариант СЗ
В сосуде лежит кусок льда. Температура льда t1 = 0°С. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20°С? Тепловыми потерями на нагрев сосуда пренебречь.
(Решение)
2011 год. 01-2 вариант. С3
В бутылке объемом V = 1 л находится гелий при нормальном атмосферном давлении. Горлышко бутылки площадью S = 2 см2 заткнуто короткой пробкой, имеющей массу m = 20 г. Если бутылка лежит горизонтально, то для того, чтобы медленно вытащить из ее горлышка пробку, нужно приложить к пробке горизонтально направленную силу F = 1 Н. Бутылку поставили на стол вертикально горлышком вверх. Какое количество теплоты нужно сообщить гелию в бутылке для того, чтобы он выдавил пробку из горлышка? (Решение)
2011 год. 01-1 вариант. С3
Один моль идеального одноатомного газа переводят из состояния 1 с температурой Т1 = 300 К в состояние 2 таким образом, что в течение всего процесса давление газа возрастает прямо пропорционально его объему. В ходе этого процесса газ получает количество теплоты Q = 14958 Дж. Во сколько раз n уменьшается в результате этого процесса плотность газа? (Решение)
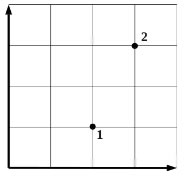 2010 год. 11 вариант. С1
2010 год. 11 вариант. С1
В кабинете физики проводились опыты с разреженным газом постоянной массы. По невнимательности ученик, отметив на графике начальное и конечное состояния газа (см. рисунок), не указал, какие две величины из трёх (давление р, объём V, температура Т) отложены по осям. В журнале осталась запись, согласно которой названные величины изменялись следующим образом: p1 < р2, V1 > V2, Τ1 < Ί2. Пользуясь этими данными, определите, какие величины были отложены на горизонтальной и вертикальной осях. Ответ поясните, указав, какие физические закономерности вы использовали. (Решение)
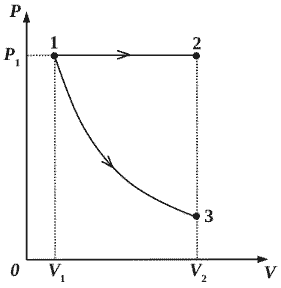 2010 год
2010 год
304 вариант СЗ
Некоторое количество одноатомного идеального газа расширяется из одного и
того же начального состояния (p1, V1) до одного и того же конечного объёма V2
первый раз по изобаре, а второй – по адиабате (см. рисунок). Отношение количества теплоты Q12, полученного газом на изобаре от нагревателя, к модулю изменения внутренней энергии газа |U3 — U1| на адиабате k = Q12/|U3 — U1| = 6 . Чему равно
отношение х работы газа на изобаре А12 к работе газа на адиабате А13? (Решение)
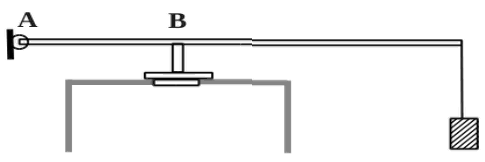 2010 год. 135 вариант. С5
2010 год. 135 вариант. С5
В цилиндр закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие площадью 5·10-4 м2, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии невесомым стержнем длиной 0,5 м, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). Расстояние АВ равно 0,1 м. К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через
580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите объём цилиндра. (Решение)
2009 год. 133 вариант. С1
В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
жидкости в сосуде? Ответ поясните. (Решение)
 2009 год. 133 вариант. С3
2009 год. 133 вариант. С3
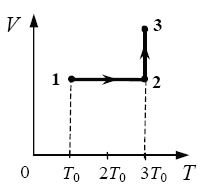
Один моль одноатомного идеального газа
переходит из состояния 1 в состояние 3 в
соответствии с графиком зависимости его объёма
V от температуры T (T0 = 100 К). На участке 2 − 3
к газу подводят 2,5 кДж теплоты. Найдите
отношение работы газа А123 ко всему количеству
подведенной к газу теплоты Q123. (Решение)
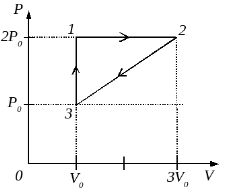 2009 год. 304 вариант. С3
2009 год. 304 вариант. С3
Постоянная масса одноатомного идеального газа совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты QH = 8 кДж. Какую работу совершают внешние силы при переходе газа из состояния 2 в состояние 3?
(Решение)
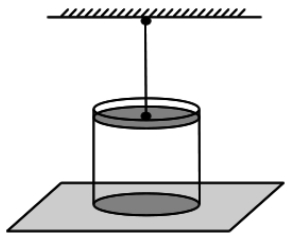 2008 год. 131 вариант. С2
2008 год. 131 вариант. С2
Разогретый сосуд прикрыли поршнем, который с помощью вертикальной нерастяжимой нити соединили с потолком. На сколько процентов от начальной понизится температура воздуха в сосуде к моменту, когда сосуд оторвется от поверхности, на которой он расположен? Масса сосуда 5 кг. Поршень может скользить по стенкам сосуда без трения. Площадь дна сосуда 125 см2. Атмосферное давление 105 Па. Тепловым расширением сосуда и поршня пренебречь. (Решение)
2008 год. 5941 вариант. С2
В калориметре находился m1 = 1 кг льда при температуре t1 = -5°С. После добавления в калориметр m2 = 25 г воды в нем установилось тепловое равновесие при температуре t = 0°С. Какова температура t2 добавленной в калориметр воды, если в калориметре оказался в итоге только лёд? Теплоёмкостью калориметра пренебречь. (Решение)
2008 год. 05205939 вариант. С2
В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз. На сколько градусов следует нагреть воздух в трубке, чтобы объём, занимаемый воздухом, стал прежним? Температура воздуха в лаборатории 300 К, а атмосферное давление составляет 750 мм рт.ст. (Решение)
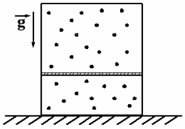 2008 год. 2 вариант. С2
2008 год. 2 вариант. С2
Вертикально расположенный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество водорода при температуре 361 К. Какая масса газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда? Толщиной поршня пренебречь. (Решение)
2007 год. 19 вариант. С2
В сосуде находится одноатомный идеальный газ, масса которого 12 г, а молярная масса 0,004 кг/моль. Вначале давление в сосуде было равно 4•105 Па при температуре 400 К. После охлаждения газа давление понизилось до 2•105 Па. Какое количество теплоты отдал газ? (Решение)
2006 год. 61 вариант. С2
В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м, закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м3- мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки мешка 2710 кг. Определите массу груза. Температура воды равна 7°С, атмосферное давление на уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. (Решение)
2006 год. 86 вариант. С2
Теплоизолированный сосуд объемом V = 2 м3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль гелия, а в другой – такое же количество молей аргона. Начальная температура гелия равна 300 К, а температура аргона 600 К. Определите давление смеси после удаления перегородки. Теплоемкостью сосуда пренебречь. (Решение)
2006 год. 33 вариант. С2
Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. При какой минимальной разности температур воздуха внутри шара и снаружи шар взлетит вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Оболочку шара считать нерастяжимой. (Решение)
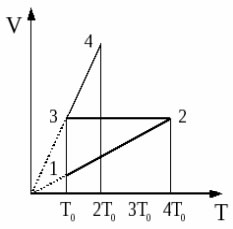
2006 год. 222 вариант. С2
С одним молем идеального одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке в координатах V-Т. Во сколько раз количество теплоты, полученное газом в процессе 1-2-3-4, больше работы газа в этом процессе? (Решение)
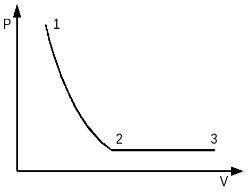 2005 год. 58 вариант. С2
2005 год. 58 вариант. С2
Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился при температуре T1 = 300 К. Затем газ изобарно нагрели, повысив температуру в 3 раза. Какое количество теплоты получил газ на участке 2-3? (Решение)
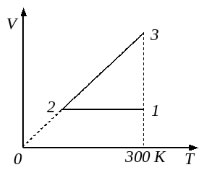
2004 год. 92 вариант. С2
10 моль одноатомного идеального газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2-3? (Решение)
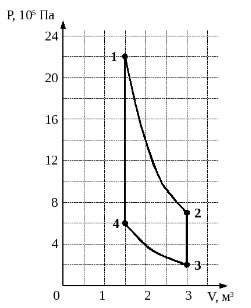 2004 год. 77 вариант. С5
2004 год. 77 вариант. С5
Идеальный одноатомный газ используется в качестве рабочего тела в тепловом двигателе. В ходе работы двигателя состояние газа изменяется в соответствии с циклом, состоящим из двух адиабат и двух изохор (см. рисунок). Вычислите КПД такого двигателя. (Решение)
2004 год. 49 вариант. С5
При электролизе воды образуется кислород О2 и водород Н2. Газы отводят в сосуд объёмом 100 л, поддерживая в нём температуру 300 К. Чему равна масса воды, которая разложилась в результате электролиза, чтобы суммарное давление в сосуде достигло 0,1 атм? Считать, что ничего не взрывается.
(Решение)
2004 год. 35 вариант. С5
Смесь одинаковых масс гелия, водорода и азота помещена в сосуд и нагрета до температуры 350 К. Плотность смеси оказалась равной 50 г/м3. Чему равно давление в сосуде? (Решение)
Источник
