Сколько молей идеального газа находится в сосуде объемом
8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В сосуде объёмом 2 л находится 10 г идеального газа при давлении 1 атм. и температуре 300 К. Во втором сосуде объёмом 4 л находится 20 г того же газа при давлении 2 атм. Чему равна температура газа во втором сосуде? (Ответ дайте в кельвинах.)
Уравнение состояния газа: [pV=nu RT=dfrac{m}{mu}RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества, (R) — универсальная газовая постоянная, (T) — температура газа, (m) — масса газа, (mu) — молярная масса газа.
Для первого сосуда: [p_1V_1=dfrac{m_1}{mu}RT_1] Для второго сосуда: [p_2V_2=dfrac{m_2}{mu}RT_2] Поделим уравнения друг на друга: [dfrac{p_1V_1}{p_2V_2}=frac{m_1T_1}{m_2T_2}] [T_2=T_1cdotdfrac{m_1}{m_2}cdotdfrac{V_2}{V_1}cdotdfrac{p_2}{p_1}=300text{ К}cdotdfrac{1}{2}cdot2cdot2=600 text{ К}]
Ответ: 600
При уменьшении абсолютной температуры газа на 300 К давление уменьшилось в 5 раз. Какова начальная температура газа, если в ходе эксперимента количество вещества уменьшилось втрое, а объём оставался постоянным? (Ответ дайте в кельвинах.)
Запишем уравнение Менделеева-Клапейрона для первого и второго состояния: [begin{cases}
p_1 V=nu_1 R T_1\
p_2 V=nu_2 R T_2
end{cases}] где (p_1) и (p_2) — давления газа в первом и втором состояниях, V — объём газа, (nu_1) и (nu_2)— количество вещества в первом и втором состояниях, (R) — универсальная газовая постоянная, (T_1) и (T_2) — абсолютная температура в первом и втором состояниях.
Поделив одно уравнение на другое, получим: [dfrac{p_1}{p_2} = dfrac{nu_1 T_1}{nu_2 T_2}] Так как (nu_1 = 3nu_2) и (p_1 = 5p_2), то: [dfrac{5p_2}{p_2} = dfrac{3nu_2cdot T_1}{nu_2cdot T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5=dfrac{3T_1}{T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_2 = 3T_1] Так как (T_2 = (T_1 – 200) К), то: [5(T_1 – 300text{ K}) = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_1 – 1500text{ K } = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
2T_1 = 1500text{ K }
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
T_1 = 750text{ K }]
Ответ: 750
На графиках приведены зависимости давления (p) и объема (V) от времени (t) для 1 моля идеального газа. Чему равна температура газа в момент (t) = 30 минут? (Ответ дайте в градусах Кельвина с точностью до 10 К.)
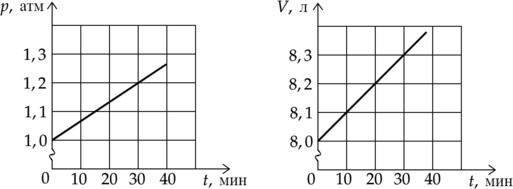
Уравнение состояния идеального газа: [displaystyle pV=nu RT,] где (p)—давление газа, (V)—объем газа, (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (T) — температура. Выразим температуру газа: [T=dfrac{pV}{nu R}] Из графика найдем давление и объем в момент времени 30 мин:
(p=1,2cdot10^5) Па
(V=8,3cdot10^{-3}text{ м$^3$})
Подставим известные и найденные значения в формулу: [T=dfrac{1,2cdot10^5text{ Па}cdot8,3cdot10^{-3}text{ м$^3$}}{1text{ моль}cdot8,31text{ }dfrac{text{Дж}}{text{моль}}} approx 120 text{ К}]
Ответ: 120
В сосуде неизменного объёма находится разреженный газ в количестве 3 моль. Во сколько раз изменится давление газа в сосуде, если выпустить из него 1 моль газа, а абсолютную температуру газа уменьшить в 2 раза?
“Демоверсия 2019”
Запишем уравнение Клапейрона – Менделеева: [p1V=nu_1RT_1=3RT_1] [p_2V=nu_2RT_2=2Rdfrac{T_1}{2}=RT_1] [dfrac{p_1}{p_2}=dfrac{3RT_1}{RT_1}=3]
Ответ: 3
В сосуде неизменного объёма находится идеальный газ. Во сколько раз нужно увеличить количество газа в сосуде, чтобы после уменьшения абсолютной температуры газа в 2 раза его давление стало вдвое больше начального?
“Досрочная волна 2020 вариант 1”
Из уравнения Клапейрона –Менделеева: [pV=nu RT] чтобы давление ((p)) увеличилось в 2 раза, при уменьшении температуры ((T)) в 2 раза, количество вещества ((nu)) должно увеличится в 4 раза
Ответ: 4
В сосуде неизменного объема находится разреженный газ в количестве 4 моль. Во сколько раз нужно увеличить абсолютную температуру газа, чтобы после удаления из сосуда 3 моль газа, давление осталось неизменным?
“Основная волна 2020 ”
Уравнение Клайперона – Менделеева: [pV=nu RT] если удалить 3 моль газа, то количество вещества уменьшится в 4 раза (nu_1=dfrac{nu}{4}), следовательно, температуру надо увеличить в 4 раза.
Ответ: 4
Источник
Пример 1.
Определите число молекул, содержащихся в 2 мм³ воды при 4°С.
Дано
Решение
V = 2·10-9 м³
T = 277 К
______________
N = ?
Число молекул определим, используя выражение
,
(1)
где ν – количество вещества, NA–число
Авогадро.
Учитывая, что ν=m/μ, где μ-молярная масса,
использовав (1), получим:
. (2)
Массу воды определим через плотность и объем : m=ρV.
Тогда формула (2) примет вид:
. (3)
Молярную массу молекулы H2O воды вычислим:
(2·1+1·16)·10-3
кг/моль=18·10-3 кг/моль.
Окончательно, из формулы (3) получаем N≈6,68·1019
.
Пример 2. Поршневой насос, объем
цилиндра которого равен 0,5л, соединен с баллоном емкостью 3л, содержащим
воздух при нормальном атмосферном давлении. Определите давление воздуха в
баллоне после 5 рабочих ходов поршня, если насос работает в режиме: а) нагнетательном,
б) разрежающем. Считать процесс изотермическим.
Дано
Решение
V1=5·10-4 м³
V2=3·10-3 м³
p0=1,013·10-3 Па
n=5
______________
pн, pр –?
а) Поршневой насос после n-рабочих
ходов в нагнетательном режиме заберет из атмосферы объем воздуха Vn=nV1
при давлении p0. Этот воздух, попадая в баллон, создает там
парциальное давление pn. Тогда, согласно закону
Бойля-Мариотта (по условию Т=const),
, отсюда . Искомое
давление воздуха в баллоне:
(1) |
б) По условию задачи воздух в баллоне занимает объем V2 при давлении р0. К концу первого
хода в разрежающем режиме та же масса воздуха займет объем V2+V1 при давлении p1.
Тогда по закону Бойля-Мариотта
, отсюда
В начале второго хода поршня объем и давление газа в баллоне
соответственно равны V2 и p1, а в конце хода – (V2+V1)
и p2, тогда
,
Следовательно, к концу n-го рабочего хода:
(2) |
Подставляя числовые значения в выражения (1) и (2), получим
pн=1,86·105 Па; pр=0,48·105
Па.
Пример 3. Идеальный газ находится
под давлением 250 кПа и занимает объем 2,5л при температуре 200К. Сначала газ
изохорно нагревают до температуры 400К. Затем, изотермически расширяя, газ
доводят до первоначального давления. После этого газ возвращают в начальное
состояние путем изобарного сжатия. Изобразите процесс графически на
рV-диаграмме. Определите давление p2 и объем V3.
Дано
Решение
p1=2,5·103 Па
V1=2,5·10-3 м³
Т1=200К,
Т2=400К
______________
p2 – ? V3-?
Построим график цикла:

При переходе газа из состояния 1 в состояние 2 осуществляется
изохорный процесс. Следовательно, по закону Шарля имеем p1/Т1=p2/Т2,
откуда
(1)
При переходе газа из состояния 3 в состояние 1 осуществляется
изобарный процесс. Тогда, согласно закону Гей-Люссака , отсюда .
Учитывая, что Т3=Т2 (точки 2 и 3
принадлежат одной изотерме), получим
. (2)
Произведем вычисления по формулам (1) и (2): p2=5·105
Па; V3= 5·10-3 м³.
Пример 4. Идеальный газ находится в
баллоне при 27°С и давлении 3·106 Па. Какой станет температура,
если из баллона будет выпущено 0,3 массы газа, а его давление понизится до
2·106 Па?
Дано
Решение
Т1=300К
p1=3·106 Па
p2=2·106 Па
k=0,3
____________________
Т2-?
Рассмотрим два состояния идеального газа. В первом состоянии
газ имеет массу m и характеризуется параметрами p1, V и T, во
втором состоянии он имеет массу и характеризуется параметрами p2,
V и Т2.
Параметры каждого из этих состояний связаны уравнением
Менделеева-Клапейрона:
,(1)
. (2)
Разделив почленно уравнение (1) на уравнение (2), имеем:
, откуда .
Произведем вычисления, получим Т2=286К
Пример 5. В закрытом сосуде объемом
2м³ находится 2г водорода и 32г кислорода при температуре 500К.
Определите: а) давление в сосуде, б) молярную массу смеси, в) плотность
смеси.
Дано
Решение
V= 2м³
Т= 500К
m1=0,002 кг
m2=0,032 кг
µ1=2·10-3кг/моль
µ2=32·10-3кг/моль
R=8,31Дж/моль·К
_______________
p-? µсм-? ρсм-?
Давление смеси определим по закону Дальтона
, (1)
где p1- давление водорода, p2-
давление кислорода.
Из уравнения Менделеева-Клапейрона:
, .(2)
С учетом (2) преобразуем выражение (1):
.(3)
Для определения молярной массы смеси используем (3) в виде
(4)
Обозначив через µсм молярную массу смеси,
запишем уравнение Менделеева-Клапейрона для смеси в виде
. (5)
Из выражений (4) и (5) получим
. (6)
Плотность смеси газов определим из:
, (7)
где m=m1+m2 – масса смеси газов. Объем смеси газов из(4):
.(8)
Решая совместно уравнения (7) и (8), получим:
.(9)
Произведем вычисления по формулам (3), (6) и (9):
р=4,2 кПа, µсм=17·10-3 кг/моль,
ρсм= 0,017кг/м³.
Пример 6. Чтобы не стать помехой
движению самолетов, олимпийский аэростат «Миша», наполненный гелием при p1=105Па
и температуре T0=300К, должен был подняться над Лужниками на высоту
h=1,5км, где плотность воздуха на 20% меньше, чем у поверхности Земли. Какова
масса M оболочки аэростата, если его объем V=500м3 (оболочку
считать герметичной и нерастяжимой).
Дано
Решение
V=500м3
p0=105Па
T0=300K
h=1.5×103м
mв=29×10-3кг/моль
mг=4×10-3кг/моль
_____________________
Mобл=?
Анализ
Предполагаем, что T =const, а V =const из условия. Условия
равновесия аэростатавыполняются на высоте h =1500м. Тогда, из закона
Архимеда:
,
где mв – масса вытесненного воздуха, mг-масса
гелия.
Решив это уравнение, ответим на вопрос задачи
Выразим mв и mг mв=rвV, где rв = 0,8rвп,
где rвп – плотность
воздуха у поверхности земли.
Тогда
, а .
Следовательно
.
Аналогично .
Тогда
.
Произведем вычисление: M=380кг.
Пример 7. Спутник погрузился в тень
Земли. При этом температура внутри спутника, равная вначале T1=300K,
упала на 1%, вследствие чего давление воздуха изменилось на величину Dp=10,5×102Па.
Определите массу воздуха в спутнике, если его объем V=10м3.
Дано
Решение
T1=300K
DT=0.01
T=3K
Dp=10,5×102Па
V=10м3
m=29×10-3кг/моль
________________
m=?
Считаем, что газ (воздух) внутри спутника является идеальным.
Запишем уравнение Менделеева – Клайперона для каждого состояния:
,(1)
,(2)
(3)
Объем V, масса m, молярная масса m газа являются постоянными. В системе трех уравнений не
известны три величины: m, p1 и р2. Следовательно,
система разрешима.
Так как температура упала, то T1=T2+DT. Вычитая из уравнения (1) уравнение (2),
получаем
.
Но p1–p2=Dp, а T1–T2=DT. Тогда приходим к уравнению:
.
Отсюда: .
Произведем вычисления: m=12кг.
Пример 8. Идеальный газ, масса
которого равна 6,1кг, занимает объем 5м3 при давлении 2∙105Па.
Определите среднюю квадратичную скорость движения молекул газа.
Дано
Решение
m=6,1кг
V=5м3
р=2∙105Па
_____________
<кв>-?
Средняя квадратичная скорость молекулы: . Из уравнения
Менделеева – Клапейрона: найдем: . Тогда .
Произведя вычисления, получим: <кв> = 700м/с
Пример 9. В баллоне находится азот
массой 4г при 300К. Определите среднюю энергию поступательного движения
молекул, находящихся в баллоне.
Дано
Решение
m=4г= 4•10-3кг
Т=300К
μ = 28•10-3кг/моль
________________
<Wn> – ?
Средняя энергия поступательного движения всех молекул определяется
выражением:
; (1)
где <εn> – средняя энергия поступательного
движения одной молекулы; N – число молекул, находящихся в баллоне. Известно,
что ,(2)
где k=1,38•10-23Дж/К – постоянная Больцмана, Т
– термодинамическая температура. Число N молекул найдем по формуле:
, (3)
где n- количество
вещества, NА =6,02•1023моль-1 – постоянная
Авогадро.
Известно, что
,(4)
где m – масса азота, μ = 28•10-3кг/моль –
молярная масса азота.
Выражение (1) с учетом (2), (3) и (4) примет вид:
. (5)
Произведем вычисления по формуле (5), получим:
<Wn>≈534 Дж.
Пример 10. Смесь водорода и гелия
при температуре 27˚C находится под давлением 2∙102Па.
Масса водорода составляет 60% от общей массы смеси. Определите концентрацию
молекул каждого газа.
Дано
Решение
Т=300К
р=2•102Па
k=1,38•10-23Дж/К
τ1=0,6
τ2=0,4
_______________
n1, n2 – ?
Масса каждого из газов определяется из соотношений
, , (1)
где m – масса смеси, τ1 и τ2
– массовые доли соответственно водорода и гелия.
С другой стороны, масса каждого из газов:
, .
(2)
Сравнив (1) и (2), получим:
,
, откуда
. (3)
Для смеси газов
. (4)
Из выражения (3) и (4) получим:
,. (5)
При заданном давлении водород и гелий можно считать идеальными
газами, подчиняющимися уравнению , отсюда (6). С учетом
(6) преобразуем соотношения (5):
, . (7)
Произведем вычисления: n1 ≈ 0,36•1023,
n2 ≈ 0,12•1023.
Пример 11. Определите полную энергию
и количество молекул воздуха между рамами окна, если площадь окна S=2м2,
расстояние между рамами ℓ=0,2м. Давление воздуха между рамами
атмосферное, а температура его линейно изменяется вдоль ℓ от t1=
-10˚C (t1 – температура наружного стекла) до t2=20˚C
(t2–температура внутреннего стекла).
Дано
Решение
S=2м2
ℓ=0,2м
Т1=263K
Т2=293K
________________
W-?
N-?
По условию задачи, воздух между рамами находится в неравновесном
состоянии, так как температура изменяется вдоль оси Оx (Рис.2), ее
распределение в объеме воздуха не изменяется со временем. В пределах
достаточно тонкого слоя толщиной dx, температуру можно считать постоянной и
равной Т. Тогда энергия
.(1)
Концентрации молекул в пределах этого слоя определив из
уравнения состояния:
.(2)
Тогда число dN молекул в объеме слоя:
,(3)
а их энергия
.(4)
По условию задачи температура между рамами изменяется
линейно:
,
(5)
где α – постоянная.
Решая совместно уравнения (2), (3), (5), получим:
.
Тогда
(6)
Постоянные α и Т0 найдем из граничных условий: при
х=0 Т=Т1, следовательно, Т0=Т1; при
х=ℓ, Т= Т2, следовательно,
,
отсюда
.
Тогда
.(7)
Полная энергия dW всех молекул в слое dx:
.
Тогда
.(8)
Произведем вычисления по формулам (7) и (8), учитывая, что
i=5, р=1,01•105Па, N = 1,06•1025, W = 1•105Дж.
Пример 12. Определите среднюю
кинетическую энергию, среднюю энергию вращательного и среднюю энергию
поступательного движения одной молекулы аммиака NH3 при 27˚C.
Дано
Решение
Т=300К
________________
<ε>-?
<εn>-?
<εвр>-?
Средняя полная энергия молекулы:
,(1)
где i – число степеней свободы, k =1,38•10-23Дж/К
– постоянная Больцмана, Т – термодинамическая температура.
Средняя энергия поступательного движения молекулы:
, (2)
где число 3 означает число степеней поступательного движения
молекул. Средняя энергия поступательного движения молекул:
.
Учтя, что молекула аммиака является четырехатомной, т.е.
ее число степеней свободы равно 6, получим:
,
откуда
. (3)
Произведем вычисления по формулам (1) и (3):
<ε>=1,24•10-20Дж; =6,2•10-21Дж.
Пример 13. Определите среднюю
арифметическую скорость молекул идеального газа, плотность которого при
давлении 35кПа составляет 0,3кг/м3.
Дано
Решение
р=35×103Па
ρ=0,3кг/м3
_______________
<υ>-?
Согласно уравнению молекулярно – кинетической теории
идеальных газов
,(1)
где n – концентрация молекул, m0–масса одной
молекулы, <υкв> – средняя квадратичная скорость
молекул.
Учитывая, что , а , получаем:
.(2)
Так как плотность газа , где m – масса газа, V
– его объем, N – число всех молекул газа, то уравнение (1) можно записать в
виде:
или .
Подставляя это выражение в формулу (2), находим искомую
среднюю арифметическую скорость:
.
Вычисляя, получаем: <υ> = 545 м/с.
Пример 14. Используя функцию
распределения молекул идеального газа по относительным скоростям , где , определите число
молекул, скорости которых меньше 0,002 наиболее вероятной скорости, если в
объеме газа содержится N=1,67×1024
молекул.
Дано
Решение
υmax =0,002 υв
N=1,67×1024
_______________
DN-?
Число dN(u) молекул, относительные скорости которых заключены
в пределах от u до u+du
,(1)
где N – число молекул в объеме газа.
По условию задачи, υmax=0,002υв,
то umax= υmax/υв=0,002.
Так как u<1, то e-u² ≈ 1-u2. Пренебрегая
u2<1, выражение (1) можно записать в виде:
.(2)
Проинтегрировав выражение (2) по u в пределах от 0 до umax,
найдем
.
Вычисляя, получаем ∆N=1016 молекул.
Пример 15. Средняя длина
<ℓ> свободного пробега молекулы углекислого газа при нормальных
атмосферных условиях равна 40 нм. Определите среднюю арифметическую скорость
<υ> молекул и среднее число <z> соударений, которые испытывает
молекула в 1 секунду.
Дано
Решение
<ℓ> = 40×10-9м
_______________
<υ>-?, <z>-?
Средняя арифметическая скорость молекул определяется по
формуле:
,(1)
где μ- молярная масса вещества.
Среднее число соударений молекулы в 1 секунду равно отношению
средней скорости <υ> молекулы к средней длине <ℓ> ее
свободного пробега:
.(2)
Произведем вычисления по формулам (1) и (2):
<υ>=362м/с, <z>=9,05·109с-1.
Пример 16. Барометр в кабине
летящего самолета все время показывает одинаковое давление р=79кПа, благодаря
чему летчик считает высоту h1 полета неизменной. Однако температура
воздуха за бортом изменилась с t=5˚C до t=1˚C. Какую ошибку
∆h в определении высоты допустил летчик? Давление р0 у
поверхности Земли считать нормальным.
Дано
Решение
р=79 ×103Па
t1=5˚C,
Т1=278К
t2=1˚C,
Т2=274К
_____________
∆h – ?
Для решения задачи воспользуемся барометрической формулой:
.
Барометр может показывать одинаковое давление р при изменении
температуры за бортом от Т1 до Т2 только в том случае,
если самолет изменяет высоту полета от h1 (которую летчик считает
неизменной), до некоторой другой h2. Запишем барометрическую формулу
для этих двух случаев:
Найдем отношение р0/р и обе части полученного
равенства прологарифмируем:
;
.
Из полученных соотношений выразим высоты h2 и h1
и найдем их разность:
.(1)
Подставим в выражение (1) значения величин (давления в отношении
р0/р можно выразить в килопаскалях, это не повлияет на окончательный
результат): ∆h=-28,5 м. Знак “–“ означает, что h2<h1
и, следовательно, самолет спустился на 28,5 метров по сравнению с предполагаемой высотой.
Пример 17. Определите, во сколько
раз отличаются коэффициенты диффузии азота (μ1=28·10-3кг/моль)
и углекислого газа (μ2=44·10-3кг/моль), если оба
газа находятся при одинаковых температуре и давлении. Эффективные диаметры
молекул этих газов считать одинаковыми.
Дано
Решение
μ1=28·10-3кг/моль
μ2=44·10-3кг/моль
________________
D1/D2-?
Коэффициент диффузии газа
,(1)
где – средняя арифметическая
скорость его молекул, – средняя длина свободного
пробега молекул. Поскольку p=nkT,
из условия задачи (p1=p2, Т1=Т2)
следует, что n1=n2. Подставив значения
<υ>,<ℓ> в формулу (1) и учитывая условие задачи,
найдем Вычисляя, получим D1/D2=1,25.
Источник
