Скорость молекул газа в сосуде
Значительная часть явлений молекулярной физики определяется скоростями молекул. Несмотря на это, нахождение скоростей молекул газа приобретает как теоретического, так и практического значения.
Виды скоростей молекул газа
Скорости газовых молекул в результате их хаотического движения отличаются как по величине, так и по направлению. Скорость данной молекулы газа в данный момент времени есть величина случайная. В молекулярно-кинетической теории газов пользуются понятиями средней ( v v v), средней квадратичной ( v к в v_{кв} vкв) и наиболее вероятной ( ν H ν_H νH) скоростей. Эти скорости задаются для равновесных состояний газа.
Средняя (или среднеарифметическая) скорость определяется уравнением
v = 1 n ∑ i = 1 n v i v=frac{1}{n}sumlimits_{i=1}^{n}{{{v}_{i}}} v=n1i=1∑nvi
где v i v_i vi – скорость i i i-й молекулы;
n n n -количество молекул.
Средняя квадратичная скорость определяется как:
v к в = v 2 = 3 k T m {{v}_{кв}}=sqrt{{{v}^{2}}}=sqrt{frac{3kT}{m}} vкв=v2 =m3kT
По этой формуле можно вычислить также скорость броуновских частиц. Конечно, при этом m m m -масса броуновской частицы.
Выражению v к в v_{кв} vкв можно придать более удобный вид, умножив числитель и знаменатель под корнем на число Авогадро и учитывая, что k N = R kN = R kN=R и m N = М mN = М mN=М,
v к в = 3 R T M {{v}_{кв}}=sqrt{frac{3RT}{M}} vкв=M3RT
Среднюю квадратичную скорость называют еще тепловой. Значение vкв для газов достаточно велики. Так, для водорода при комнатной температуре v к в = 1 , 9 ⋅ 1 0 3 v_{кв} = 1,9 · 10^3 vкв=1,9⋅103 м/с, то есть около 2 км/с.
Тепловая скорость, как видно из уравнения, пропорциональна корню температуры и обратно пропорциональна корню массы. Это обстоятельство определяет, что тепловое движение- достаточно интенсивно для молекул, заметно для микроскопически малых частиц, которые осуществляют броуновское движение, и совершенно незаметно для тяжелых тел.
Экспериментальное определение скоростей газовых молекул
Большой интерес представляет непосредственное экспериментальное определение скоростей газовых молекул. Оно является прямым подтверждением многих результатов и положений молекулярно-кинетической теории. Впервые такое исследование провел А. Штерн в 1920 г. Источником атомов, скорость которых измерялась, в опыте Штерна был молекулярный пучок атомов серебра Ag. Схема установки приведены на рис. 1. На оси системы двух коаксиальных цилиндрических поверхностей натянуто платиновый провод, покрытый слоем серебра.
Примечание
В других опытах использовали также висмут, кадмий, цезий.
Проволока разогревается электрическим током. Так, при температуре около 1300°С серебро с поверхности проволоки испаряется. Таким образом создавался линейный источник «Ag-лучей» и в камере цилиндров, воздух из которой предварительно откачивался при давлении 1,3 · 10-4 Па, образовывался одноатомный газ серебра. Часть атомов серебра через диафрагмы s1 и s2 проходила, образуя молекулярный пучок, к поверхности внешнего цилиндра, где оседала на прозрачной пластинке, создавая слой в виде узкой полосы.
Рис. 1
На первой стадии опыта Штерна установка находится в состоянии покоя. При достижении равновесного состояния (температура проволоки достигала определенного значения, которое определяли по её свечению) атомы серебра оседали у точки а1. На второй стадии опыта оба цилиндра приводились в достаточно быстрое вращение с частотой 41,7 с-1.
При этом атомы серебра, двигаясь в вакууме прямолинейно, оседали у точки b. Смещение полосы объясняется тем, что пока атомы серебра пролетают по инерции путь r, внешний цилиндр успевает вернуться на угол φ = ω t φ = ωt φ=ωt, то есть каждая точка внешнего цилиндра смещается на расстояние Δ s = ω r t Δs = ωrt Δs=ωrt, где ω ω ω -угловая скорость его вращения; t t t -время, за который атомы серебра проходят путь r. Таким образом,
t = r v = Δ s ω r t=frac{r}{v}=frac{Delta s}{omega r} t=vr=ωrΔs
где v v v – скорость атомов серебра.
Отсюда
v = ω r 2 Δ s v=frac{omega {{r}^{2}}}{Delta s} v=Δsωr2
Измеряя смещение полос атомов серебра Δ s Δs Δs и угловую скорость вращения прибора, можно определить скорость атомов серебра. Она приблизительно описывалась выражением
( 3 , 5 k T m ) 1 2 {{left( 3,5frac{kT}{m} right)}^{frac{1}{2}}} (3,5mkT)21
что согласуется со средней скоростью молекул, которые определяются по формуле
v = 8 k T π m v=sqrt{frac{8kT}{pi m}} v=πm8kT
Результаты опытов Штерна показали, что на самом деле картина структуры полосы сложнее.
Смещенная возле точки b полоса была не резко ограниченной, а размытой (рис. 2).
Рис. 2
Несмотря на то, что атомы серебра имеют разные скорости, более быстрым атомам должны соответствовать меньшие смещения, а тем более медленным – большие. Таким образом, результаты опыта Штерна вполне передают реальную картину теплового движения молекул.
Тест по теме «Скорость движения молекул»
Источник
В этом разделе приводятся некоторые следствия, вытекающие из формул (3.29) и (3.30). В качестве примера на рис. 3.3 изображены две кривые, соответствующие распределениям f(v) молекул кислорода O2 по абсолютным величинам скоростей при температурах Т1 = 300 К и Т2 = 1 300 К.
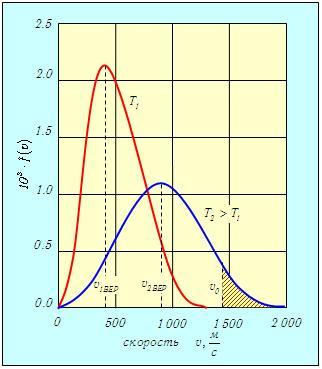
Рис. 3.3. Распределение молекул кислорода по скоростям при разных температурах T1 = 300 К и T2 = 1 300 К
Наиболее вероятная скорость. При бесконечно малых и неограниченно больших значениях скоростей функция распределения стремится к нулю
то есть такие предельные значения скоростей маловероятны в системе. Следовательно, при каком-то значении скорости функция f(v) достигает своего максимума.
Наиболее вероятная скорость vВЕР – это скорость, отвечающая максимальному значению функции распределения.
Ее можно найти, решая уравнение
откуда следует, что
(3.31) |
Иными словами, наиболее вероятной называется скорость, вблизи которой на единичный интервал приходится наибольшее число молекул. В этой точке f(v) принимает максимальное значение:
(3.32) |
Соотношения (3.31), (3.32) могут быть полезны для анализа изменения функции распределения при изменении температуры газа или при изменении рода газа, то есть массы молекул. Отметим, что как следует из (3.26) – (3.29), распределение Максвелла зависит не отдельно от массы молекул и отдельно от температуры газа, а от их отношения . Поэтому распределение не только «буквенно» но и численно одно и тоже, например, для молекулярного водорода при температуре и для гелия при температуре .
С ростом температуры наиболее вероятная скорость vВЕР (3.31) увеличивается, то есть максимум функции f(v) сдвигается вправо (см. рис. 3.3), Т2 > Т1. При этом f(vВЕР) уменьшается, то есть кривая становится более пологой. Так же деформируется кривая, если температура постоянна, но масса молекул уменьшается. Напомним, что при любых деформациях функции распределения f(v) площадь под кривыми постоянна и равна единице в соответствии с формулой (3.30).
Относительное количество молекул, скорость которых превышает некоторое значение v0, определяется выражением
(3.33) |
На графике (см. рис. 3.3) этому интегралу соответствует лежащая справа от v0часть площади (отмечена штриховкой), ограниченная кривой f(v) и осью скоростей. Как видно из рис. 3.3, относительное количество молекул, имеющих скорости, превышающие v0, растет с повышением температуры.
В заключение этого раздела заметим, что во всех формулах для функции распределения и характерных скоростей входит отношение массы молекулы к постоянной Больцмана
Умножая числитель и знаменатель на число Авогадро NAи учитывая, что
– молярная масса газа, a
– универсальная газовая постоянная, мы всюду можем использовать это отношение в наиболее удобной для конкретной задачи форме
Распределение молекул по величинам безразмерной скорости. Если при графическом изображении функции распределения Максвелла (3.29) по оси абсцисс откладывать скорости молекул v, то форма кривой и положение максимума будут зависеть от массы молекул и от температуры газа. Но если по горизонтальной оси откладывать отношение скорости к наиболее вероятной скорости, то есть безразмерную скорость
то для всех температур и любых масс молекул (любых газов) получится одна и та же кривая (рис. 3.4).
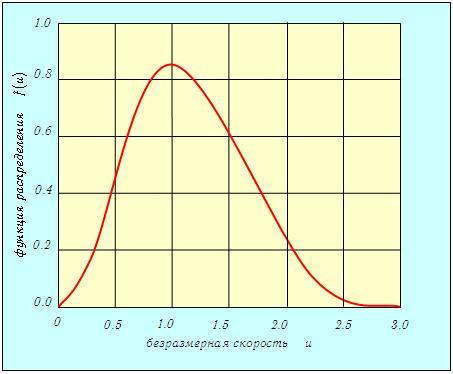
Рис. 3.4. Распределение Максвелла по величинам безразмерной скорости
Сделав замену переменной
в (3.29) и учитывая, что
получим распределение Максвелла в форме
(3.34) |
Эта формула и соответствующий ей график (см. рис. 3.4) удобны для решения многих задач.
Пример. Найдем, какая часть общего числа молекул кислорода имеет при температуре 27 °С скорости, отличающиеся от наиболее вероятной не более, чем на 1 %; а также скорости в интервале 562-572 м/с.
Произведем необходимые вычисления. Чтобы ответить на первый вопрос задачи, учтем, что u = 1 при v = vВЕР. Величина интервала du = 0,02. Следовательно,
Вычислим наиболее вероятную скорость:
Найдем отношение v = 562 м/с к vВЕР = 395 м/с
Определим по кривой (см. рис. 3.4) значение функции f(u) при u = 1,42. Получаем f(u) = 0,62. Ширина интервала Dv = 10 м/с (Du = 10/395 = 0,0253). Следовательно, доля молекул в этом интервале
Интересно отметить, что молекула кислорода проходит за секунду путь, равный в среднем 0,4 км. Но не нужно забывать о соударениях молекул. Из-за них молекула по прямой движется очень недолго, и ее путь представляет собой ломаную линию. Поэтому молекула, двигаясь с огромной скоростью по отдельным звеньям ломаной траектории, передвигается от слоя к слою газа со сравнительно небольшой скоростью.
Средняя арифметическая скорость. Знание функции распределения молекул по скоростям f(v) дает возможность найти среднее значение скорости, а также любой величины, являющейся функцией скорости, например квадрата скорости v2или кинетической энергии молекулы mv2/2.
Средняя арифметическая скорость <v> – это отношение суммы абсолютных величин скоростей всех молекул в системе к числу этих молекул.
Разобьем интервал всех возможных значений скорости от 0 до бесконечности на малые интервалы Dvi. Каждому интервалу соответствует количество молекул
(3.35) |
Так как интервалы Dvi, малы, то можно приближенно считать скорости молекул данного интервала одинаковыми и равными vi. Сумма значений скоростей молекул интервала
(3.36) |
Сумма значений скоростей всех молекул
(3.37) |
Разделив эту сумму на число молекул, получим выражение для средней арифметической скорости
(3.38) |
Переходя от суммы к интегралу, получаем
(3.39) |
Вычисляя интеграл, получаем среднюю арифметическую скорость молекул
(3.40) |
Среднеквадратичная скорость. Чтобы найти среднее значение произвольной функции L(v) скорости, нужно эту функцию умножить на функцию распределения и проинтегрировать по всем возможным значениям скорости:
(3.41) |
В частности, при L(v) = v отсюда находится <v>.
Среднее значение квадрата скорости равно отношению суммы квадратов скоростей всех молекул системы к общему числу молекул. Таким образом,
(3.41) |
Среднеквадратичная скорость – это корень квадратный из среднего значения квадрата скорости молекул
Следует отметить, что характерные скорости отличаются друг от друга лишь численными множителями, причем
(3.43) |
а зависимость от Т и m0(или m) у них одинаковая.
Через среднеквадратичную скорость выражается средняя кинетическая энергия поступательного движения молекул
(3.44) |
Этот результат находится в согласии с формулой (1.14) кинетической теории идеальных газов и с законом о равнораспределении энергии, который гласит, что на каждую степень свободы молекулы приходится энергия kBТ/2. Три степени свободы поступательного движения молекулы как раз соответствуют полученному здесь результату (3.44). В сущности, именно для того, чтобы получить такое соответствие, мы выбрали должным образом коэффициент α в (3.26).
Эксперимент по проверке распределения Максвелла. Необходимо еще раз подчеркнуть, что установленный Максвеллом закон распределения молекул по скоростям и все вытекающие из него следствия справедливы только для газа, находящегося в равновесии.
Закон справедлив для любого числа молекул N, если только это число достаточно велико. Закон Максвелла – статистический, а законы статистики выполняются тем точнее, чем к большему числу одинаковых объектов они применяются. При малом числе объектов могут наблюдаться значительные отклонения от предсказанной статистики – флуктуации.
Экспериментальное определение распределения скоростей молекул было осуществлено впервые О. Штерном в 1920 г. Исследовалось распределение по скоростям одноатомных молекул паров металлов (Ag или Pt), из которых была изготовлена нить, расположенная на оси двух цилиндров. Нить нагревалась электрическим током, и металл испарялся (см. рис 3.5).
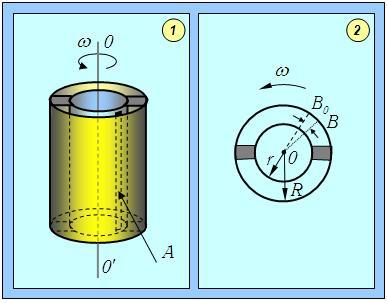
Рис. 3.5 Схема опыта Штерна: 1 – вид установки сбоку; 2 – вид установки сверху
Молекулы, прошедшие через щель во внутреннем цилиндре, летели по прямой и оседали на стенке холодного внешнего цилиндра. Если привести всю установку во вращение (щель все время против точки В0), то молекулы, обладающие большой скоростью v, попадут в некоторую точку вблизи В0, а более медленные затратят на путь больше времени и попадут в точки, отстоящие дальше от В0. Следует обратить внимание, что вылетающие молекулы движутся по прямой, они не участвуют во вращательном движении. Поскольку молекулы в зависимости от скорости попадают в разные точки внешнего цилиндра, то исследуя толщину слоя металла, осевшего на его стенку, можно составить представление о распределении молекул по скоростям.
Найдем распределение молекул по расстояниям S от точки В0 до места их попадания на стенку цилиндра. Если R и r – радиусы большого и малого цилиндров, соответственно (см. рис.), то время полета от щели до стенки цилиндра
За это время цилиндр повернется на угол
где ω – угловая скорость вращения установки. Соответственно, точка попадания будет смещена относительно В0 на расстояние
Подставляя сюда время полета, получаем связь скорости молекулы с расстоянием S:
Подставляя, в свою очередь, полученное выражение в распределение Максвелла и учитывая, что
находим распределение молекул по расстояниям S:
(мы опускаем выражение для нормировочной постоянной С).
Опыты Штерна подтвердили справедливость закона, установленного Максвеллом.
Источник
©2015- 2021 zdamsam.ru Размещенные материалы защищены законодательством РФ.
| ||
Основные представления молекулярно-кинетической теории газов, как известно, базируются на модели идеального газа. Эта простая модель позволяет объяснить многие свойства газов в широком интервале давлений и температур. Прежде всего, надо освоиться с порядком величин, характеризующих молекулярную теорию газов. Много ли молекул находится, скажем, в единице объема воздуха? Лучше всего за единицу объема взять не 1 м3, а 1 см3. Получится нагляднее. Ранее была получена формула P = nkT, связывающая давление, оказываемое газом на стенки сосуда с числом молекул в единице объема n и абсолютной температурой Т. Величина k – это постоянная Больцмана, одна из универсальных физических констант, надежно определенная опытным путем. Подсчитаем число молекул воздуха при нормальных условиях, то есть при давлении в 1 атмосферу, что соответствует 1,01·105 Па, и при температуре Т = 273 К. Постоянную Больцмана возьмем из таблицы физических констант. . Итак, . Полученное число молекул заключено в 1 м3, так как все величины были выражены в системе СИ. В 1 cм3 будет в миллион раз меньше, потому что в 1 м3 миллион cм3. Учитывая это, запишем . Это число называется числом Лошмидта. С чем сравнить это число? Если бы в 1 cм3 было миллион молекул, то , если бы миллион миллионов, то . На самом же деле число Лошмидта еще в десять миллионов раз больше. Этот пример прекрасно характеризует масштабы, с которыми приходится иметь дело при изучении молекулярно-кинетической теории газов. В технике очень часто используются приборы, в которых создается вакуум, то есть откачивается газ. Самые совершенные вакуумные насосы откачивают воздух до давления Па. Но и при этом в каждом кубическом сантиметре остаются десятки тысяч молекул. Обсудив этот вопрос, перейдем к рассмотрению средней длины свободного пробега. Раньше было получено, что молекулы в единицу времени сталкиваются в среднем z раз и эта величина равна , где r – радиус молекулы, v – средняя скорость ее движения, n – число молекул в единице объема. Число это легко подсчитать. По порядку – это миллиарды столкновений в единицу времени при нормальных условиях. Путь, проходимый молекулой между двумя столкновениями, называется средней длиной свободного пробега. Получим среднюю длину свободного пробега, поделив путь, проходимый ею за единицу времени, на число столкновений в единицу времени. Но этот путь численно равен скорости, следовательно, длина свободного пробега равна . Оценим для воздуха при нормальных условиях . При этом расчете радиус молекулы, полученный экспериментально . Длина свободного пробега примерно равна миллионной доли миллиметра. Это при нормальных условиях. Если же уменьшать давление, то будет уменьшаться n-число молекул в единице объема. Но , то есть линейно зависит от давления. И если давление уменьшать, то соответственно будет увеличиваться длина свободного пробега. Когда длина свободного пробега становится больше размеров сосуда, молекулы не сталкиваются друг с другом, а только со стенками сосуда. В этом случае вакуум считается высоким. Умножим левую и правую часть основного уравнения молекулярно-кинетической теории на объем одного моля газа Отсюда можно получить среднюю квадратичную скорость молекул, которая приписывается газовым молекулам, чтобы объяснить производимое ими давление. Действительно, в этом уравнении величины Р и V легко измеримы, величины же NA и m, хотя и неизмеримы непосредственно в отдельности, но произведение их, входящее в формулу, представляет собой численно молекулярную массу. Подсчитаем среднюю квадратичную скорость молекул воздуха при нормальных условиях: . Принимая для воздуха µ = 29 , получим . Как велика эта скорость? Сравним ее со скоростью звука при тех же условиях. Скорость звука, равная 332 м/с, меньше скоростей молекул воздуха. В соответствии с расчетной формулой молекулы газа с меньшей молярной массой имеют большую скорость. Так для водорода при тех же условиях средняя квадратичная скорость равна 1840 м/с. Пуля в стволе винтовки разгоняется ударами молекул газа, получающегося при взрыве пороха, поэтому создатели оружия стремятся увеличить температуру газа, толкающего пулю. Пуля вылетает из ствола, со скоростью большей скорости звука, но меньшей средней квадратичной скорости молекул газа. При выводе основного уравнения молекулярно-кинетической теории предполагалось, что скорости молекул неодинаковы. При рассмотрении вопроса о скоростях молекул Максвелл исходил из основной идеи, заключающейся в том, что сколь бы велико ни было число молекул, сколь бы ни были разнообразны условия столкновений молекул друг с другом, в среднем весь этот хаос должен удовлетворять одному непременному условию: состояние газа не должно меняться со временем. Это, в свою очередь, означает, что распределение молекул по скоростям должно быть не произвольным, а вполне определенным. Нельзя ставить вопрос о том, сколько молекул обладает заданной скоростью. Дело в том, что число молекул, имеющих математически точно заданную скорость, равно нулю. Число различных значений скорости бесконечно большое, а число молекул, хотя и велико, но конечно. Поэтому вопрос надо ставить следующим образом: какая часть, или лучше, какая доля молекул (от общего числа) обладает скоростями, лежащими в некотором интервале вблизи заданной скорости? Пусть в единице объема находится n молекул. Обозначим через dn число молекул, обладающих скоростью в интервале от v до v + dv . Очевидно, что эти dn тем больше, чем шире этот интервал, , или , где а – некоторый коэффициент пропорциональности. Этот коэффициент не постоянный, так как в равных интервалах скоростей число молекул должно быть различно. Учитывая это, запишем, что а есть функция от скорости . Учтем еще, что dn зависит и от числа молекул n в единице объема. Теперь запишем, что формула для величины dn будет выглядеть так: , или , Величина справа в этой формуле – доля молекул, скорости которых лежат в интервале от v до v + dv . Функция называется функцией распределения молекул по скоростям. Смысл функции распределения ясен из этой формулы. Перепишем ее так и положим интервал скоростей , тогда и численно равна доле молекул, скорости которых лежат в единичном интервале скоростей вблизи скорости v. Максвелл получил теоретически эту функцию. Вывод ее требует применения высшей математики, поэтому приводим ее без вывода. , По кривой распределения можно графически определить относительное число молекул, обладающих скоростями в любом заданном интервале. Это число выражается площадью заштрихованной полосы, основанием которой является заданный интервал скоростей. Тогда, очевидно, что площадь, ограниченная кривой и осью скоростей, равна единице. Распределение молекул по скоростям зависит от температуры газа. На рис.10 приведены кривые распределения молекул азота для температур 20oС и 500oС. Повышение температуры увеличивает скорости всех молекул, растет наивероятнейшая скорость, вся кривая смещается в сторону больших температур. Площади, ограниченные этими кривыми и осью скоростей одинаковы для разных температур. Естественно, что максимумы кривых при увеличении температуры понижаются. Кривые, отвечающие разным температурам, могут быть приведены к одной, если по оси ординат откладывать не скорости v, а относительную скорость. . В этом случае функция распределения Максвелла . На рис.11 дан точный график функции в зависимости от U. Этот график позволяет легко найти число молекул, обладающих скоростями в любом интервале при любой температуре для любого газа. В качестве примера рассмотрим такую задачу. Какая доля молекул кислорода обладает скоростью, лежащей между и при температуре 300 К? Сначала определим наивероятнейшую скорость: . Относительная скорость . Согласно графику при функция . Величина . Величина . Отсюда искомое число , то есть 0,41 % молекул кислорода при Т = 300 К обладают скоростями в интервале от 790 м/с до 800 м/с.
Легко связать это смещение S со скоростью молекул v. Молекулы достигают стенки за время t, равное . За это время каждая точка на стенке сосуда пройдет путь , где – угловая скорость вращения прибора. Из этого выражения получим время t: . Приравнивая выражение для времени, получим или . По этой формуле и рассчитывалась скорость. Но след в точке В был не таким, как в точке А, он был размазан. Этого и следовало ожидать, так как атомы серебра вылетают с различными скоростями. Измерение плотности осевшего серебра позволило подтвердить справедливость распределения Максвелла молекул по скоростям. Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: |
Источник

