Скорость вытекания из сосуда
Закон Торричелли
Итальянский ученый Эванджелиста Торричелли, изучавший движение жидкостей,
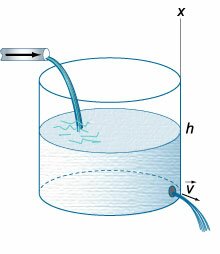
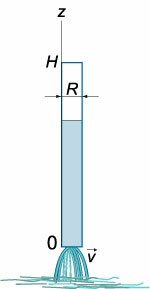
в (1643) году экспериментально обнаружил, что скорость вытекания жидкости через малое отверстие на дне открытого сосуда (рисунок (1)) описывается формулой:
[v = sqrt {2gh} ,]
где (h) − высота уровня жидкости над отверстием, (g) − гравитационная постоянная.
| |
Рис.1 | Рис.2 |
Такая же формула описывает скорость тела, свободного падающего с высоты (h) в поле тяжести Земли в вакууме.
В действительности, найденная формула не совсем точна. В более точном приближении скорость жидкости зависит от формы и размера отверстия, от вязкости жидкости и режима течения. Поэтому,
формула Торричелли часто записывается с дополнительным множителем (varphi:)
[v = varphisqrt {2gh} ,]
где коэффициент (varphi) близок к (1.) Значения параметра (varphi) для отверстий различной формы и размера можно найти в гидравлических справочниках.
Вытекание жидкости из тонкой трубки
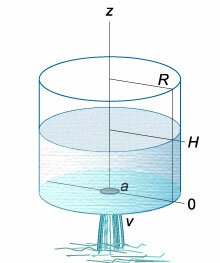
Вытекание жидкости из тонкой длинной трубки (рисунок (2)) имеет ряд особенностей. Здесь важную роль играют капиллярные эффекты, обусловленные
поверхностным натяжением и смачиванием вследствие контакта со стенками трубки.
Скорость вытекания жидкости из капиллярных трубок приблизительно пропорциональна высоте столба жидкости над отверстием, то есть
[v = kh,]
где (k) − некоторая константа, зависящая от вязкости жидкости, геометрии и материала трубки.
Далее мы будем описывать вытекание жидкости с помощью дифференциальных уравнений из сосудов обоих типов (широкого и тонкого).
Дифференциальное уравнение вытекания жидкости
Данное дифференциальное уравнение можно вывести, рассматривая баланс жидкости в сосуде. Возьмем, например, цилиндрический сосуд с широким основанием, радиус
которого равен (R.) Предположим, что жидкость вытекает через малое отверстие радиуса (a) на дне сосуда (рисунок (3)).
|
|
Рис.3 | Рис.4 |
Скорость жидкости описывается формулой Торричелли:
[v = sqrt {2gz} ,]
где (z) − высота жидкости над отверстием. Тогда поток жидкости определяется выражением:
[q = – pi {a^2}sqrt {2gz} .]
Здесь (pi {a^2}) соответствует площади отверстия, через которое вытекает жидкость, а знак “минус” означает,
что уровень жидкости уменьшается по мере ее вытекания из резервуара.
Уравнение баланса жидкости в резервуаре описывается следующим образом:
[frac{{dV}}{{dt}} = q.]
Поскольку изменение объема (dV) можно выразить как
[dV = Sleft( z right)dz,]
то мы получаем дифференциальное уравнение
[frac{{Sleft( z right)dz}}{{dt}} = qleft( z right).]
Подставим функцию (qleft( z right)) в это уравнение:
[frac{{Sleft( z right)dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
Поперечное сечение ({Sleft( z right)}) цилиндрического сосуда не зависит от высоты (z) и равно
[Sleft( z right) = pi {R^2},]
где (R) − радиус основания цилиндра. Тогда
[require{cancel}
cancel{pi} {R^2}frac{{dz}}{{dt}} = – cancel{pi} {a^2}sqrt {2gz} .
]
В результате получаем уравнение с разделяющимися переменными:
[frac{{dz}}{{sqrt z }} = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt.]
Теперь проинтегрируем полученное уравнение, считая, что начальный уровень жидкости составляет (H,) и за время (T) он уменьшается до (0:)
[
{intlimits_H^0 {frac{{dz}}{{sqrt z }}} = – intlimits_0^T {frac{{{a^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow 2left[ {left. {left( {sqrt z } right)} right|_H^0} right] = – frac{{{a^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow 2sqrt H = frac{{{a^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow sqrt {2H} = frac{{{a^2}}}{{{R^2}}}sqrt g T.}
]
Отсюда следует выражение для полного времени вытекания жидкости (T:)
[T = frac{{{R^2}}}{{{a^2}}}sqrt {frac{{2H}}{g}} .]
Интересно, что в предельном случае (a = R) (когда площади отверстия и самого цилиндра равны), полученная
формула преобразуется в известную формулу (T = sqrt {largefrac{{2H}}{g}normalsize}, )
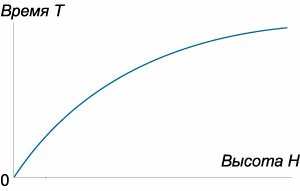
которая определяет время падения материального тела с высоты (H.) Зависимость времени (T) от высоты (H) схематически показана на рисунке (4.)
Аналогично можно описать вытекание жидкости и из сосуда другой формы.
Вывести дифференциальное уравнение вытекания жидкости из конического сосуда и определить полное время вытекания (T.)
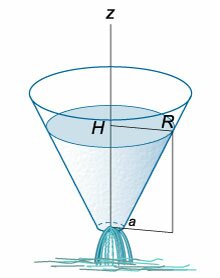
Радиус верхнего основания конического сосуда равен (R,) а радиус нижнего основания (a.) Начальная уровень жидкости составляет (H) (рисунок (5)).
| |
Рис.5 | Рис.6 |
Изменение уровня жидкости на высоте (z) описывается дифференциальным уравнением
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right),]
где (Sleft( z right)) − площадь поперечного сечения сосуда на высоте (z,) а (qleft( z right)) − поток жидкости, зависящий от высоты (z.)
Принимая во внимание геометрию сосуда, можно предположить, что закон Торричелли выполняется. Поэтому, можно записать:
[qleft( z right) = – pi {a^2}sqrt {2gz} ,]
где (a) − радиус отверстия на дне конического сосуда. Учитывая, что отверстие достаточно малое, осевое сечение можно рассматривать как треугольник
(рисунок (6) выше). Из подобия треугольников следует, что
[frac{R}{H} = frac{r}{z}.]
Следовательно, площадь поверхности жидкости на высоте (z) будет равна
[
{Sleft( z right) = pi {r^2} }
= {pi {left( {frac{{Rz}}{H}} right)^2} }
= {frac{{pi {R^2}{z^2}}}{{{H^2}}}.}
]
Подставляя (Sleft( z right)) и (qleft( z right)) в дифференциальное уравнение, имеем:
[frac{{pi {R^2}{z^2}}}{{{H^2}}}frac{{dz}}{{dt}} = – pi {a^2}sqrt {2gz} .]
После простых преобразований получаем следующее дифференциальное уравнение:
[{z^{largefrac{3}{2}normalsize}}dz = – frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt.]
Проинтегрируем обе части, учитывая, что уровень жидкости уменьшается от начального значения (H) до нуля за время (T:)
[
{intlimits_H^0 {{z^{largefrac{3}{2}normalsize}}dz} = – intlimits_0^T {frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} dt} ,};;
{Rightarrow left. {left( {frac{{{z^{largefrac{5}{2}normalsize}}}}{{frac{5}{2}}}} right)} right|_0^H = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} left[ {left. {left( t right)} right|_0^T} right],};;
{Rightarrow frac{2}{5}{H^{largefrac{5}{2}normalsize}} = frac{{{a^2}{H^2}}}{{{R^2}}}sqrt {2g} T,};;
{Rightarrow frac{1}{5}sqrt {frac{{2H}}{g}} = frac{{{a^2}}}{{{R^2}}}T,};;
{Rightarrow T = frac{{{R^2}}}{{5{a^2}}}sqrt {frac{{2H}}{g}} .}
]
Здесь мы снова видим аналогию с падением материального тела с высоты (H) в гравитационном поле Земли. Как известно,
время падения описывается формулой:
[T = sqrt {frac{{2H}}{g}}. ]
Если мы сравним этот результат со случаем вытекания жидкости из цилиндрического сосуда, то видно, что при тех же самых
значениях (H, R) и (a) время вытекания жидкости из конического сосуда ровно в (5) раз меньше, чем из цилиндра (хотя
объем конического сосуда меньше лишь в (3) раза!). Такие целочисленные отношения в природе выглядят удивительными, не правда ли?
Исследовать вытекание жидкости из тонкой трубки радиусом (R) и высотой (H,) считая трубку полностью заполненной жидкостью.
|
|
Рис.7 | Рис.8 |
Аналогично разобранным выше примерам, мы можем записать уравнение баланса жидкости на некоторой произвольной высоте (z) в следующей форме:
[Sleft( z right)frac{{dz}}{{dt}} = qleft( z right).]
В данном случае площадь поперечного сечения (Sleft( z right)) является константой:
[Sleft( z right) = S = pi {R^2},]
и поток жидкости, вытекающей из сосуда, определяется формулой:
[qleft( z right) = – kz,]
где (k) зависит от размера отверстия, смачиваемости и других параметров.
В результате получаем простое дифференциальное уравнение:
[pi {R^2}frac{{dz}}{{dt}} = – kz,]
или после разделения переменных:
[frac{{dz}}{z} = – frac{k}{{pi {R^2}}}dt.]
Теперь это уравнение можно проинтегрировать, считая, что уровень жидкости уменьшается с высоты (H) до (h) за время от (0) до (t:)
[
{intlimits_H^h {frac{{dz}}{z}} = – intlimits_0^t {frac{k}{{pi {R^2}}}dt} ,};;
{Rightarrow left. {left( {ln z} right)} right|_h^H = frac{k}{{pi {R^2}}}t,};;
{Rightarrow t = frac{{pi {R^2}}}{k}left( {ln H – ln h} right) = frac{{pi {R^2}}}{k}ln frac{H}{h}.}
]
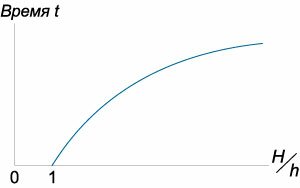
Зависимость времени (t) от отношения (largefrac{H}{h}normalsize) показана схематически на рисунке (8.)
Данная кривая аналогична зависимости времени (T) от высоты (H) для широкого цилиндрического сосуда, для которого справедлив закон Торричелли.
Интересно, что в данной простой модели время вытекания жидкости (t) формально стремится к бесконечности при (h to 0.)
Источник
Рассмотрим бак с водой. В днище бака выполнено отверстие. Задача — рассчитать, как будет выливаться вода из бака, а также проанализировать расчет в Simscape Fluids для применения такого источника жидкости в других схемах. Расчеты по аналитическим формулам для простоты работы с единицами измерения делал в Mathematica. Решение ОДУ расхода и построение графика уровня от времени также выполнено в Mathematica.
Время истечения жидкости — Схема
Схема вот:
Схема для моделирования задачи в Simscape Fluids.
Аналитические расчеты
Характеристики бака и аналитические расчеты:
Характеристики бака и расчеты. Блокнот Mathemetica из двух ячеек (in[11] и in[22]). — диаметр отверстия в баке, — площадь отверстия, — площадь основания бака (бак с прямыми стенками, например — вертикальный цилиндр), — высота уровня воды в баке в начале процесса, — ускорение свободного падения, — плотность воды, — кинематическая вязкость.
— скорость потока через отверстие, вычисляется по формуле Торричелли. В англоязычной литературе, эта формула называется законом Торричелли. Расход — это просто скорость потока , умноженная на площадь отверстия . UnitConvert преобразует единицы расхода в л/мин. Время вытекания воды из бака составило по аналитическим расчетам 1016.8 секунды.
Время истечения жидкости — Модель Simscape Fluids
Теперь, результаты моделирования:
Результаты запуска модели Simscape. Vt — объем воды в баке (л), Q — расход из бака (л/мин).
Результат похож на ожидания. На первом графике отображается объем воды в баке. Первоначальный объем равен 125 л, согласно геометрии бака и высоте уровня. По истечении почти 1000 секунд времени, бак опустошится . Расход остается ненулевым даже при нулевом объеме ввиду специфики математической модели бака. На верхнем графике можно заметить даже отрицательный объем. Стоит учитывать это обстоятельство при моделировании более сложных схем. Начальный же расход вполне точно соответствует полученному при аналитическом расчете.
Коэффициент Pipeline pressure loss coefficient принимается для бака равным единице. Также следует внимательнее относиться к установке начальных значений переменным. На рисунке ниже показана настройка блока Бак. В расчетах за начальную переменную принимается исходный уровень, а не объем. Показаны соответствующие настройки приоритета начальных значений, в данном случае, объем 20 л игнорируется (поэтому крестик). При установке равного приоритета обоим начальным значениям переменных, результаты моделирования данной схемы будут неточными.
Установка начальных значений для переменных блока Tank. Красным крестиком отмечена начальная переменная без приоритета. Объём в начале симуляции не равен 20 литрам, он составляет 125 литров и определяется параметрами бака и начальной переменной с более высоким приоритетом. Она отмечена зеленой галочкой.
Аналитическое уравнение
Решение аналитического уравнения.
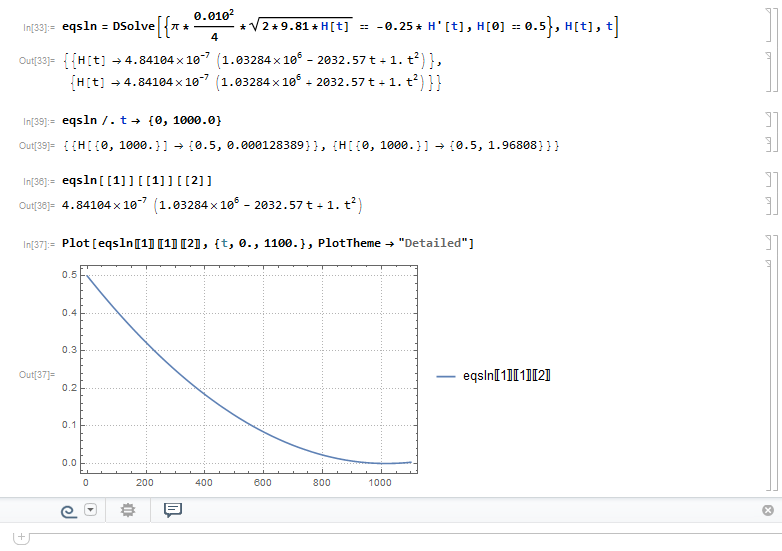Решение ОДУ для определения зависимости уровня от времени по аналитическим выражениям. Кликните для увеличения.
Как видно из рисунка, дифференциальное уравнение представляет собой равенство, в левой части которого расход, полученный при помощи уравнения Торричелли, а в правой части — расход по своему определению. По идее, расход это , но так как стенки бака прямые, площадь мы выносим за производную. Таким образом, уравнение имеет вид:
Его решение показано синей линией на графике уровня от времени. График уровня проходит минимум при .
Источник
Ìåõàíèêà ñïëîøíûõ ñðåä. Ëåêöèè.
Âûòåêàíèå æèäêîñòè ÷åðåç îòâåðñòèå â ñîñóäå.
Ïóñòü æèäêîñòü, çàïîëíÿþùàÿ ñîñóä, ïîä äåéñòâèåì ñèëû òÿæåñòè âûòåêàåò èç íåãî ÷åðåç îòâåðñòèå â áîêîâîé ñòåíêå, ðàñïîëîæåííîå âáëèçè äíà ñîñóäà (ðèñ. 3.6).  îòâåðñòèå âñòàâëåíà ãîðèçîíòàëüíàÿ òðóáêà ñ çàêðóãëåííîé âíóòðåííåé êðîìêîé, íàïðàâëÿþùàÿ âûòåêàþùóþ ñòðóþ âîäû. Çàêðóãëåííàÿ êðîìêà îáåñïå÷èâàåò ïîëíîå çàïîëíåíèå òðóáêè âûòåêàþùåé æèäêîñòüþ.
| Ðèñ. 3.6. |
Ðàçîáüåì òåêóùóþ æèäêîñòü íà òðóáêè òîêà. Îäíà èç òàêèõ òðóáîê èçîáðàæåíà íà ðèñóíêå 3.6. Õîòÿ ìû è íå çíàåì, êàê âûãëÿäÿò ýòè òðóáêè, îäíàêî âñå îíè íà÷èíàþòñÿ íà ñâîáîäíîé ïîâåðõíîñòè æèäêîñòè è çàêàí÷èâàþòñÿ íà âûõîäíîì òîðöå ñëèâíîé òðóáêè. Åñëè ïëîùàäü îòâåðñòèÿ òðóáêè S çíà÷èòåëüíî ìåíüøå ïëîùàäè ñâîáîäíîé ïîâåðõíîñòè S0, òî ïðè èñòå÷åíèè æèäêîñòè åå îïóñêàþùàÿñÿ ñ íåêîòîðîé ñêîðîñòüþ v0 ïîâåðõíîñòü áóäåò îñòàâàòüñÿ ãîðèçîíòàëüíîé. Ýòî îçíà÷àåò. ÷òî êîíñòàíòà, âõîäÿùàÿ â óðàâíåíèå Áåðíóëëè (3.14), áóäåò îäèíàêîâà äëÿ âñåõ òðóáîê òîêà:
Çäåñü H – âûñîòà óðîâíÿ æèäêîñòè â ñîñóäå. Ïîýòîìó ñêîðîñòü èñòå÷åíèÿ æèäêîñòè v îïðåäåëÿåòñÿ èç óðàâíåíèÿ
| (3.17) |
ãäå p0 – àòìîñôåðíîå äàâëåíèå íà ñâîáîäíîé ïîâåðõíîñòè è ó ñëèâíîé òðóáêè. Ïîñêîëüêó SS0, òî èç óñëîâèÿ íåñæèìàåìîñòè (3.2) ñëåäóåò, ÷òî v0v. Ñ ó÷åòîì ýòîãî ñêîðîñòü èñòå÷åíèÿ èç (3.17) ïîëó÷àåòñÿ ðàâíîé
| (3.18) |
Ýòà ôîðìóëà íîñèò íàçâàíèå ôîðìóëû Òîðè÷åëëè, ïîñêîëüêó áûëà ïîëó÷åíà Òîðè÷åëëè, æèâøåì äî Áåðíóëëè. Ñðàçó áðîñàåòñÿ â ãëàçà, ÷òî ñêîðîñòü èñòå÷åíèÿ æèäêîñòè èç ñîñóäà òàêàÿ æå, êàê è ïðè åå ñâîáîäíîì ïàäåíèè ñ âûñîòû H.  ýòîì íåò íè÷åãî óäèâèòåëüíîãî, ïîñêîëüêó âÿçêîñòüþ ìû ïðåíåáðåãëè, à ðàáîòà ñèë àòìîñôåðíîãî äàâëåíèÿ íàä òðóáêîé òîêà ðàâíà íóëþ. Ïîýòîìó, êàê è ïðè ñâîáîäíîì ïàäåíèè òåë â îòñóòñòâèå ñîïðîòèâëåíèÿ âîçäóõà, ïðè ðàùåíèå êèíåòè÷åñêîé ýíåðãèè ðàâíî ðàáîòå ñèëû òÿæåñòè:
Ñïðàâåäëèâîñòü ôîðìóëû Òîðè÷åëëè ìîæíî ëåãêî ïðîâåðèòü, åñëè íà âûõîäíóþ òðóáêó íàäåòü êóñîê ãèáêîãî øëàíãà è âûòåêàþùóþ ñòðóþ âîäû íàïðàâèòü ââåðõ ïîä íåáîëüøèì íàêëîíîì ê âåðòèêàëè (ðèñ. 3.7). Ñòðóÿ ïîäíèìåòñÿ ïðàêòè÷åñêè äî óðîâíÿ ïîâåðõíîñòè æèäêîñòè. Åñëè æå ñòðóþ íàïðàâèòü âåðòèêàëüíî ââåðõ, òî âçëåòàþùèå ââåðõ ÷àñòèöû æèäêîñòè, âçàèìîäåéñòâóÿ ñ ïàäàþùèìè âíèç ÷àñòèöàìè, íå ñìîãóò ïîäíÿòüñÿ íà âûñîòó H.
| Ðèñ. 3.7. |
Èíòåðåñíî îòìåòèòü, ÷òî òðóáêè òîêà æèäêîñòè ðàñïîëîæåíû ïðåèìóùåñòâåííî áëèæå ê ñòåíêå ñîñóäà ñ îòâåðñòèåì, â òî âðåìÿ êàê ó ïðîòèâîïîëîæíîé (ëåâîé íà ðèñ. 3.8) ñòåíêè æèäêîñòü ïðàêòè÷åñêè ìàëîïîäâèæíà. Ýòî îçíà÷àåò, ÷òî íà ëåâóþ ñòåíêó äåéñòâóþò ñèëû äàâëåíèÿ, êîòîðîå ëåãêî ïîñ÷èòàòü, èñïîëüçóÿ ëèíåéíûé çàêîí íàðàñòàíèÿ ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñ ãëóáèíîé, äàâàåìîé ôîðìóëîé (2.11). Ðàñ÷åò ñèë äàâëåíèÿ, äåéñòâóþùèõ íà ïðàâóþ ñòåíêó, òðåáóåò ãèäðîäèíàìè÷åñêîãî ðåøåíèÿ çàäà÷è. Îäíàêî è áåç òàêîãî ðàñ÷åòà ÿñíî, ÷òî â òðóáêå òîêà, ïðèìûêàþùåé ê ïðàâîé ñòåíêå, äàâëåíèå íà êàæäîé ãëóáèíå áóäåò ìåíüøå ñîîòâåòñòâóþùåãî ýòîé ãëóáèíå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ. Ýòî îçíà÷àåò, ÷òî ðàâíîäåéñòâóþùàÿ ñèë äàâëåíèÿ, äåéñòâóþùèõ íà îáå ñòåíêè, íàïðàâëåíà â ñòîðîíó, ïðîòèâîïîëîæíóþ íàïðàâëåíèþ èñòå÷åíèÿ æèäêîñòè. Ïîä äåéñòâèåì ýòîé ñèëû, íàçûâàåìîé òàêæå ðåàêòèâíîé, ñîñóä, ïîñòàâëåííûé íà êîëåñà, ìîæåò ïðèäòè â äâèæåíèå. Âåëè÷èíó ýòîé ñèëû ëåãêî ïîñ÷èòàòü ñ èñïîëüçîâàíèåì ôîðìóëû Òîðè÷åëëè. Ïî 3-ìó çàêîíó Íüþòîíà èñêîìàÿ ðåàêòèâíàÿ ñèëà ðàâíà ïî âåëè÷èíå ñèëå, ñ êîòîðîé ñòåíêè ñîñóäà äåéñòâóþò íà âîäó, ñîîáùàÿ åå (ïî 2-ìó çàêîíó Íüþòîíà) ïðèðàùåíèå èìïóëüñà â íàïðàâëåíèè èñòå÷åíèÿ. Ïîñêîëüêó ìàññà, âûòåêàþùàÿ ÷åðåç îòâåðñòèå ñ ñå÷åíèåì S ðàâíà , òî èçìåíåíèå èìïóëüñà â åäèíèöó âðåìåíè ñîñòàâèò âåëè÷èíó Ïîýòîìó ðåàêòèâíàÿ ñèëà
| (3.19) |
| Ðèñ. 3.8. |
Îòìåòèì, ÷òî åñëè áû ìû îøèáî÷íî ïðèíÿëè, ÷òî ðàñïðåäåëåíèå äàâëåíèé ñ ãëóáèíîé ó ïðàâîé ñòåíêè áûëî òàêîå æå, êàê ó ëåâîé, òî ðåàêòèâíàÿ ñèëà ïîëó÷èëàñü áû âäâîå ìåíüøåé:
| (3.20) |
ãäå – âåëè÷èíà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ íà ãëóáèíå H, S – ïëîùàäü îòâåðñòèÿ â ïðàâîé ñòåíêå.
Îäíàêî ìîæíî äîáèòüñÿ îäèíàêîâîãî (ãèäðîñòàòè÷åñêîãî) ðàñïðåäåëåíèÿ äàâëåíèé ó îáåèõ ñòåíîê, åñëè êîíåö òðóáêè ñ îñòðîé êðîìêîé áóäåò îòñòîÿòü îò ïðàâîé ñòåíêè, êàê ïîêàçàíî íà ðèñ. 3.9.  ýòîì ñëó÷àå ðåàêòèâíàÿ ñèëà ìîæåò îïðåäåëÿòüñÿ ñ ïîìîùüþ ôîðìóëû (3.20). Åñëè æå åå âû÷èñëÿòü ïðè ïîìîùè (3.19), òî â ýòîé ôîðìóëå íàäî âìåñòî ñå÷åíèÿ òðóáêè S ïîäñòàâèòü ñå÷åíèå ñòðóè âîäû â òðóáêå SB=kS, ãäå êîýôôèöèåíò èñòå÷åíèÿ k1/2. Ïðè òàêîì èñòå÷åíèè òðóáêà áóäåò çàïîëíåíà æèäêîñòüþ ïðèáëèçèòåëüíî íàïîëîâèíó.
| Ðèñ. 3.9. |
Ðåàêòèâíóþ ñèëó ìîæíî óâåëè÷èòü, åñëè ïðåæäå âñåãî ïîâûñèòü ñêîðîñòü èñòå÷åíèÿ æèäêîñòè. Äëÿ ýòîãî ñëåäóåò èñïîëüçîâàòü çàìêíóòûé ñîñóä ñ îòâåðñòèåì, ïðè ýòîì íàä ñâîáîäíîé ïîâåðõíîñòüþ æèäêîñòè ñîçäàåòñÿ äàâëåíèå p1>p0. Òîãäà ñêîðîñòü èñòå÷åíèÿ æèäêîñòè èç óðàâíåíèÿ Áåðíóëëè ïîëó÷àåòñÿ ðàâíîé:
| (3.21) |
à ðåàêòèâíàÿ ñèëà âîçðàñòàåò ëèíåéíî ñ ïîâûøåíèåì èçáûòî÷íîãî äàâëåíèÿ íàä ñâîáîäíîé ïîâåðõíîñòüþ æèäêîñòè.
Ãèäðîðåçàíèå.
Åñëè ñîçäàòü î÷åíü âûñîêîå èçáûòî÷íîå äàâëåíèå, íàïðèìåð, 5000 àòì = 5*10 Í/ì2, òî ñêîðîñòü èñòå÷åíèÿ âîäû v = 1000 ì/ñ. Åñëè òàêóþ ñòðóþ íàïðàâèòü íà êàêîé-ëèáî òâåðäûé ìàòåðèàë, òî åãî ïîâåðõíîñòü áóäåò ïîäâåðæåíà ãèäðîäèíàìè÷åñêîìó äàâëåíèþ Òàêîå
îãðîìíîå äàâëåíèå â ðÿäå ñëó÷àåâ ìîæåò ïðåâîñõîäèòü ïðåäåë ïðî÷íîñòè íåêîòîðûõ ìàòåðèàëîâ, è ïîñëåäíèå áóäóò ðàçðóøàòüñÿ ïîä äåéñòâèåì ñòðóè. Ñî âòîðîé ïîëîâèíû 80-õ ãîäîâ ïîëó÷èëî ðàçâèòèå íîâîå íàïðàâëåíèå â îáðàáîòêå ìàòåðèàëîâ – ãèäðîðåçàíèå.  ýòîé òåõíîëîãèè âîäÿíîé íîæ – âûñîêî-ñêîðîñòíàÿ ñòðóÿ âîäû ñ äèàìåòðîì èãëû – ëåãêî ðåæåò ìàòåðèàëû òîëùèíîé â íåñêîëüêî ñàíòèìåòðîâ ñî ñêîðîñòüþ ðåçàíèÿ íåñêîëüêî äåñÿòêîâ ñàíòèìåòðîâ â ìèíóòó. Äëÿ ðåçêè ìåòàëëîâ, òâåðäûõ ñïëàâîâ, áåòîíà è äðóãèõ ìàòåðèàëîâ â ñòðóþ äîáàâëÿþò àáðàçèâíûé ïîðîøîê. Ýòî ïîçâîëÿåò çíà÷èòåëüíî óâåëè÷èòü ãèäðîäèíàìè÷åñêîå äàâëåíèå è ïîâûñèòü ïðîèçâîäèòåëüíîñòü è âîçìîæíîñòè ãèäðîðåçàíèÿ.
Ñîñóä Ìàðèîòòà.
Âåñüìà ïîó÷èòåëüíûì äëÿ ïîíèìàíèÿ äâèæåíèÿ æèäêîñòè ÿâëÿåòñÿ èñòå÷åíèå æèäêîñòè èç ñîñóäà Ìàðèîòòà. Îí ïîçâîëÿåò îáåñïå÷èòü ïîñòîÿííóþ ñêîðîñòü âûòåêàíèÿ æèäêîñòè èç ñîñóäà, íåñìîòðÿ íà ïîíèæåíèÿ åå óðîâíÿ. Äëÿ ýòîãî â ñîñóä ÷åðåç ãåðìåòè÷íóþ ïðîáêó â åãî ãîðëîâèíó ââîäèòñÿ òðóáî÷êà, ñîîáùàþùàÿñÿ ñ àòìîñôåðîé (ðèñ. 3.10). Ñêîðîñòü âûòåêàíèÿ îïðåäåëÿåòñÿ ïî ôîðìóëå Òîðè÷åëëè , ãäå h – âûñîòà íèæíåãî êîíöà òðóáêè íàä îòâåðñòèåì. Ýòî ïðîèñõîäèò ïîòîìó, ÷òî ïðè íåçíà÷èòåëüíîì èñòå÷åíèè æèäêîñòè èç ïîëíîñòüþ çàïîëíåííîãî ñîñóäà äàâëåíèå ïîä ïðîáêîé áóäåò ìåíüøå àòìîñôåðíîãî, à äàâëåíèå â ãîðèçîíòàëüíîé ïëîñêîñòè, ñîâïàäàþùåé è íèæíèì êîíöîì òðóáêè, ðàâíî àòìîñôåðíîìó. Ñêîðîñòü âûòåêàíèÿ ëåãêî ðåãóëèðóåòñÿ âåðòèêàëüíûì ïåðåìåùåíèåì òðóáêè. Åñëè êîíåö òðóáêè íàõîäèòñÿ íà óðîâíå h=0 èëè íèæå îòâåðñòèÿ, òî æèäêîñòü íå âûòåêàåò âîâñå.
| Ðèñ. 3.10. |
Óñëîâèå íåñæèìàåìîñòè äâèæóùåéñÿ æèäêîñòè.
Ðàâåíñòâî (3.2), ÿâëÿþùååñÿ óñëîâèåì íåñæèìàåìîñòè, ñâÿçûâàåò ñêîðîñòè äâèæóùåéñÿ æèäêîñòè â äâóõ ðàçëè÷íûõ ñå÷åíèÿõ. Ìåæäó òåì, êàê íà ýòî íåîäíîêðàòíî îáðàùàëîñü âíèìàíèå â ïðåäûäóùèõ ëåêöèÿõ, â ôèçèêå âàæíî îïåðèðîâàòü ñ ðàâåíñòâàìè èëè óðàâíåíèÿìè, îòíåñåííûìè ê îäíîé òî÷êå ïðîñòðàíñòâà.
Äëÿ ýòîãî ðàññìîòðèì äåôîðìàöèþ äâèæóùåãîñÿ êóáè÷åñêîãî ýëåìåíòà æèäêîñòè. Åñëè åãî îáúåì ÷åðåç ìàëûé îòðåçîê âðåìåíè íå èçìåíÿåòñÿ, òî ñóììà äèàãîíàëüíûõ ýëåìåíòîâ òåíçîðà äåôîðìàöèè ðàâíà íóëþ, ò.å.
Çäåñü ux, uy è uz- ñìåùåíèÿ ãðàíåé êóáèêà â íàïðàâëåíèè ñîîòâåòñòâóþùèõ îñåé êîîðäèíàò. Îäíàêî ýòè ñìåùåíèÿ ñâÿçàíû ñî ñêîðîñòÿìè äâèæåíèÿ ãðàíåé (à òî÷íåå, ÷àñòèö æèäêîñòè, íàõîäÿùèõñÿ â äàííûé ìîìåíò íà ýòèõ ãðàíÿõ):
Ïîäñòàâëÿÿ ýòè ðàâåíñòâà â (3.22), ïîëó÷àåì ëîêàëüíîå (îòíîñÿùååñÿ ê îäíîé òî÷êå ïðîñòðàíñòâà) óñëîâèå íåñæèìàåìîñòè â âèäå
| (3.22) |
 ôèçèêå äëÿ îïèñàíèÿ âåêòîðíûõ ïîëåé, à â íàøåì ñëó÷àå ðå÷ü èäåò î âåêòîðíîì ïîëå ñêîðîñòåé v=v(x,y,z,t), èñïîëüçóåòñÿ ïîíÿòèå äèâåðãåíöèè (èñòîêà) ïîëÿ â äàííîé òî÷êå ïðîñòðàíñòâà.  äåêàðòîâîé ñèñòåìå êîîðäèíàò âûðàæåíèå äëÿ div v èìååò âèä:
| (3.23) |
Äèâåðãåíöèÿ âåêòîðà ÿâëÿåòñÿ ñêàëÿðíîé ôóíêöèåé êîîðäèíàò è âðåìåíè è ëåãêî ðàññ÷èòûâàåòñÿ, åñëè èçâåñòíû êîìïîíåíòû âåêòîðíîãî ïîëÿ (â íàøåì ñëó÷àå vx, vy è vz). Ïîýòîìó óñëîâèå (3.22) ïîñòîÿíñòâà îáúåìà íåñæèìàåìîé æèäêîñòè çàïèñûâàåòñÿ êðàòêî:
| (3.24) |
Îòìåòèì, ÷òî óðàâíåíèå (3.24) ÿâëÿåòñÿ îäíèì èç îñíîâíûõ óðàâíåíèé ãèäðîäèíàìèêè íåñæèìàåìîé æèäêîñòè.
Ñëåäóåò îòìåòèòü, ÷òî èìååòñÿ ìíîæåñòâî âåêòîðíûõ ïîëåé, êàê, íàïðèìåð, ýëåêòðè÷åñêîå E=E(x,y,z,t) è ìàãíèòíîå B=B(x,y,z,t) ïîëÿ è äð., ïðè îïèñàíèè êîòîðûõ òàêæå øèðîêî èñïîëüçóåòñÿ ïîíÿòèå äèâåðãåíöèè: div E èëè div B è ò.ä. Õîòÿ îíà îïðåäåëÿåòñÿ â ñîîòâåòñòâèè ñ (3.23), ââîäèòñÿ, îäíàêî, íåñêîëüêî èç äðóãèõ ñîîáðàæåíèé, ïîñêîëüêó â ýëåêòðîäèíàìèêå íå èäåò ðå÷ü î äâèæåíèè è äåôîðìàöèè ýëåìåíòà ìàòåðèàëüíîé ñðåäû.
Íà ïðèìåðå âåêòîðíîãî ïîëÿ ñêîðîñòåé v=v(x,y,z,t) ïîÿñíèì ôóíäàìåíòàëüíûé ñìûñë ïîíÿòèÿ äèâåðãåíöèè.
Äëÿ ýòîãî ðàññìîòðèì íåïîäâèæíûé ýëåìåíòàðíûé îáúåì ïðîñòðàíñòâà. dV=dxdydx è ïîñ÷èòàåì îáúåì æèäêîñòè, âòåêàþùèé è âûòåêàþùèé èç ýòîãî îáúåìà çà åäèíèöó âðåìåíè.
Ââåäåì ïîíÿòèå ýëåìåíòàðíîãî ïîòîêà âåêòîðà ñêîðîñòè v ÷åðåç ìàëåíüêóþ ïëîùàäêó dS:
| (3.25) |
ãäå dS=ndS – âåêòîð, íàïðàâëåííûé ïî íîðìàëè n ê ýëåìåíòàðíîé ïëîùàäêå. ßñíî, ÷òî ïîòîê (3.25) ðàâåí îáúåìó æèäêîñòè, ïåðåñåêàþùåé ïëîùàäêó dS çà åäèíèöó âðåìåíè (ðèñ. 3.12). Îí äîïóñêàåò òàêæå íàãëÿäíóþ ãåîìåòðè÷åñêóþ èíòåðïðåòàöèþ.  ñàìîì äåëå, â ñîîòâåòñòâèè ñ îïðåäåëåíèåì ëèíèé òîêà, äàííûì â íà÷àëå ýòîé ëåêöèè, èõ ãóñòîòà õàðàêòåðèçóåò ñêîðîñòü òå÷åíèÿ. Ïîýòîìó âåëè÷èíå ñêîðîñòè âñåãäà ìîæíî ïîñòàâèòü â ñîîòâåòñòâèå êîëè÷åñòâî ëèíèé òîêà, ïåðåñåêàþùèõ ïëîùàäêó ñ dS=1 è n || v. Òîãäà ïîòîê dNv â (3.25) áóäåò õàðàêòåðèçîâàòüñÿ ÷èñëîì ëèíèé, ïåðåñåêàþùèõ ïëîùàäêó ïðè åå ïðîèçâîëüíîé îðèåíòàöèè.
| Ðèñ. 3.12. |
Òåïåðü ëåãêî ïîñ÷èòàòü áàëàíñ ìåæäó âòåêàþùåé è âûòåêàþùåé æèäêîñòüþ äëÿ ýëåìåíòàðíîãî îáúåìà, èçîáðàæåííîãî íà ðèñ. 3.12. Äëÿ ýòîãî âîññòàíîâèì âíåøíèå íîðìàëè ïî âñåì 6-òè ãðàíÿì êóáèêà è ïîñ÷èòàåì ïîòîêè æèäêîñòè ÷åðåç åãî ãðàíè. Ëåãêî ïîíÿòü, ÷òî ïîëîæèòåëüíîå çíà÷åíèå ïîòîêà áóäåò äëÿ âûòåêàþùåé æèäêîñòè, à îòðèöàòåëüíîå – äëÿ âòåêàþùåé. Åñëè ñêîðîñòü â öåíòðå êóáèêà v(x,y,z) èçìåíÿåòñÿ ïðè ïðèáëèæåíèè ê ñîîòâåòñòâóþùèì ãðàíÿì, òî ïðè âû÷èñëåíèè òàêîãî ïîòîêà ýòî íåîáõîäèìî ó÷åñòü. Ðåçóëüòèðóþùèé ïîòîê îïðåäåëèòñÿ ñëåäóþùèì îáðàçîì:
| (3.26) |
Ðàçäåëèâ ëåâóþ è ïðàâóþ ÷àñòè (3.26) íà dxdydz è ïåðåõîäÿ ê ïðåäåëó, ïîëó÷àåì
| (3.27) |
Òàêèì îáðàçîì, äèâåðãåíöèÿ âåêòîðà ñêîðîñòè ÷èñëåííî ðàâíà ïîòîêó æèäêîñòè ÷åðåç ïîâåðõíîñòü åäèíè÷íîãî îáúåìà. Åñëè æèäêîñòü íåñæèìàåìà, òî, åñòåñòâåííî, ýòîò ïîòîê äîëæåí áûòü ðàâåí íóëþ. Ãðàôè÷åñêè ïîñëåäíåå èíòåðïðåòèðóåòñÿ êàê ðàâåíñòâî êîëè÷åñòâà âõîäÿùèõ è âûõîäÿùèõ ëèíèé òîêà äëÿ ýòîãî îáúåìà. Ýòî, â ñâîþ î÷åðåäü, îçíà÷àåò, ÷òî â îêðåñòíîñòè òî÷êè, ãäå div v=0, ëèíèè òîêà íå ïðåðûâàþòñÿ. Ïîýòîìó ðàâåíñòâî div v=0 íàçûâàþò óñëîâèåì íåðàçðûâíîñòè.
Èç øêîëüíîãî êóðñà ôèçèêè èçâåñòíî, ÷òî ñèëîâûå ëèíèè ýëåêòðîñòàòè÷åñêîãî ïîëÿ (àíàëîã ëèíèé òîêà) ïðåðûâàþòñÿ òîëüêî íà çàðÿäàõ. Ïîýòîìó äëÿ îáëàñòåé, íå çàíÿòûõ çàðÿäàìè, ìû òàêæå âïðàâå íàïèñàòü . Ñèëîâûå ëèíèè èíäóêöèè ìàãíèòíîãî ïîëÿ B âñåãäà çàìêíóòû, ïîýòîìó âî âñåõ ñëó÷àÿõ div B=0.
Íàçàä | Âïåðåä
Ïîñìîòðåòü êîììåíòàðèè[3]
Источник