Скорость жидкости вытекающей из стенки сосуда автор

Лекция 5. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, НАСАДКОВ И ИЗ-ПОД ЗАТВОРОВ

Рассмотрим различные случаи истечения жидкости из резервуаров, баков, котлов через отверстия и насадки (коротки трубки различной формы) в атмосферу или пространство, заполненное газом или той же жидкость. В процессе такого истечения запас потенциальной энергии, которым обладает жидкость, находящаяся в резервуаре, превращается в кинетическую энергию свободной струи.

Основным вопросом, который интересует в данном случае, является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.

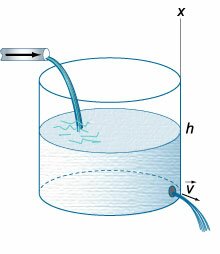
Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис.5.1).

Рис. 5.1. Истечение из резервуара через малое отверстие

Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму, показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.

Рис. 5.2. Истечение через круглое отверстие

Степень сжатия оценивается коэффициентом сжатия.

где Sс и Sо – площади поперечного сечения струи и отверстия соответственно; dс и dо – диаметры струи и отверстия соответственно.

Скорость истечения жидкости через отверстие такое отверстие

где Н – напор жидкости, определяется как

φ- коэффициент скорости

где α – коэффициент Кориолиса;

ζ- коэффициент сопротивления отверстия.

Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:

Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.

В итоге получаем расход

где ΔР – расчетная разность давлений, под действием которой происходит истечение.

При помощи этого выражения решается основная задача – определяется расход.

Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рис.5.3 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости

где ν – кинематическая вязкость.

При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи (рис.5.4). Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.

Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5).

Рис. 5.5. Схема несовершенного сжатия струи

Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, то струя по выходе из отверстия сжимается в меньшей степени, чем из резервуара неограниченных размеров, как это было описано в п.5.1.

При истечении жидкостей из цилиндрического резервуара круглого сечения через круглое отверстие, расположенное в центре торцевой стенки, при больших числах Re коэффициент сжатия для идеальной жидкости можно найти по формуле, представленной Н.Е. Жуковским:

где n – отношение площади отверстия Sо к площади поперечного сечения резервуара S1

Расход жидкости при несовершенном сжатии

где напор Н нужно находить с учетом скоростного напора в резервуаре

Часто приходится иметь дело с истечением жидкости не в атмосферу, а в пространство, заполненное этой же жидкостью (рис.5.6). такой случай называется истечением под уровень, или истечением через затопленное отверстие.

Рис. 5.6. Истечение по уровень

В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.

Скорость истечения в сжатом сечении струи

где φ – коэффициент скорости;

Н – расчетный напор,

Расход жидкости равен

Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.

Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.

Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без закругления входной кромки (рис. 5.7). На практике такой насадок часто получается в тех случаях, когда выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в газовую среду может происходить в двух режимах.

Первый режим – безотрывный режим. При истечении струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров отверстия из насадка выходит полным сечением (рис.5.7).

Рис. 5.7. Истечение через насадок

Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа Рейнольдса, определяется по эмпирической формуле:

Так как на выходе из насадка диаметр струи равен диаметру отверстия, то коэффициент сжатия ε = 1 и, следовательно, μ = φ , а коэффициент сопротивления ζ = 0,5.

Если составить уравнение Бернулли для сжатого сечения 1-1 и сечения за насадком 2-2 и преобразовать его, то можно получить падение давления внутри насадка

P2 – P1 0,75Hgρ

При некотором критическом напоре Нкр абсолютное давление внутри насадка (сечение 1-1) становится равным нулю (P1 = 0), и поэтому

Следовательно, при Н > Нкр давление P1 должно было бы стать отрицательным, но так как в жидкостях отрицательных давлений не бывает, то первый режим движения становится невозможным. Поэтому при Н Нкр происходит изменение режима истечения, переход от первого режима ко второму (рис.5.8).

Рис. 5.8. Второй режим истечения через насадок

Второй режим характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится точно таким же, как и из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, а расход уменьшается благодаря сжатию струи.

При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от описанного выше. Но при Н > Нкр перехода ко второму режиму не происходит, а начинается кавитационный режим.

Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода, а на втором – очень низкий коэффициент расхода. Недостатком также является возможность кавитации при истечении под уровень.

Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки или устройства конического входа. На рис.5.9 даны различные типы насадков и указаны значения соответствующих коэффициентов.

Рис. 5.9. Истечение жидкости через насадки а – расширяющиеся конические; б – сужающиеся конические; в – коноидальные; г – внутренние цилиндрические

Конически сходящиеся и коноидальные насадки применяют там, где необходимо получить хорошую компактную струю сравнительно большой длины при малых потерях энергии (в напорных брандспойтах, гидромониторах и т.д.). Конически сходящиеся насадки используют для увеличения расхода истечения при малых выходных скоростях.

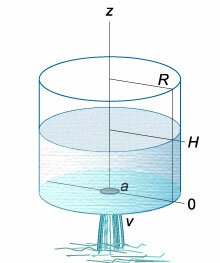
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рис.5.10).

Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.

Рис. 5.10. Схема опорожнения резервуара

Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровнеS, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:

где dh – изменение уровня жидкости за время dt.

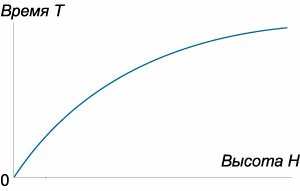
Отсюда время полного опорожнения сосуда высотой Н

Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного опорожнения

Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.

Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 5.12) выразим зависимость переменной площади S от h:

где l – длина цистерны; D – диаметр цистерны.

Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным

Во многих водозаборных и водопропускных гидротехнических сооружениях расходы воды проходят через отверстия, перекрываемые затворами. Затворы поднимают на определенную высоту над дном и пропускают через отверстия необходимые расходы. Чаще всего на гидромелиоративных сооружениях устраивают отверстия прямоугольного сечения, истечение из которых и рассмотрим.

Отверстия могут быть незатопленными (истечение свободное) и затопленными, когда уровень воды за затвором влияет на истечение.

Если отверстие незатопленное, то вытекающая из-под затвора струя находится под атмосферным давлением (рис. 5.13). При истечении через затопленное отверстие струя за затвором находится под некоторым слоем воды (рис. 5.14).

Рис. 5.13. Истечение из-под затвора через незатопленное отверстие

Когда затвор приподнят над дном, вытекающая из-под него струя испытывает сжатие в вертикальной плоскости. На расстоянии, примерно равном высоте отверстия а (высоте поднятия затвора), наблюдается наиболее сжатое сечение. Глубина в сжатом сечении hc связана с высотой отверстия а следующей зависимостью:

hc = ε’a

где ε’ – коэффициент вертикального сжатия струи.

Коэффициент вертикального сжатия ε’ зависит от отношения высоты отверстия а к напору (глубине воды перед затвором) Н. Для ориентировочных расчетов можно принимать ε’ = 0,64.

Если составить уравнение Бернулли для сечений, проведенных перед затвором и в сжатом сечении, после преобразований получим:

где φ – коэффициент скорости,

где Н0 – напор с учетом скорости подхода,

Тогда расход при истечении из-под затвора при незатопленном отверстии определится по формуле:

где S – площадь отверстия, S = ab.

Рис. 5.14. Истечение из-под затвора при затопленном отверстии

При истечении через затопленное отверстие (рис. 5.14) расход определится по формуле:

где hz – глубина в том сечении, где наблюдается максимальное сжатие истекающей из-под затвора струи.

Глубина hz определяется из зависимости

в которой

а hб – глубина в отводящем канале (бытовая глубина).

Если вытекающая из отверстия или насадка струя попадает на неподвижную стенку, то она с определенным давлением воздействует на нее. Основное уравнение, по которому вычисляется давление струи на площадку, имеет вид

На рис. 5.15 приведены наиболее часто встречающиеся в практике ограждающие поверхности (преграды) и уравнения, по которым вычисляется давление струи на соответствующую поверхность.

Величина давления струи, естественно, зависит от расстояния насадка до преграды. С увеличением расстояния струя рассеивается и давление уменьшается. Соответствующие исследования показывают, что в данном случае струя может быть разбита на три характерные части: компактную, раздробленную и распыленную (рис.5.16).

В пределах компактной части сохраняется цилиндрическая форма струи без нарушения сплошности движения. В пределах раздробленной части сплошность потока нарушается, причем струя постепенно расширяется. Наконец, в пределах распыленной части струи происходит окончательный распад потока на отдельные капли.

Рис. 5.15. Взаимодействие струи жидкости с неподвижной поверхностью

Рис. 5.16. Составные части свободной струи

Источник

Рисунок из «Гидродинамики» Д. Бернулли: из-за течения по трубе, компенсирующего расход через правое отверстие О, давление в трубе меньше, чем в сосуде слева.

Зако́н Берну́лли[1] (также уравне́ние Берну́лли[2][3], теоре́ма Берну́лли[4][5] или интегра́л Берну́лли[2][6][7]) устанавливает зависимость между скоростью стационарного потока жидкости и её давлением. Согласно этому закону, если вдоль линии тока давление жидкости возрастает, то скорость течения убывает, и наоборот. Количественное выражение закона в виде интеграла Бернулли является результатом интегрирования уравнений гидродинамики идеальной жидкости[2] (то есть без вязкости и теплопроводности).

История[править | править код]

Для случая несжимаемой жидкости результат, эквивалентный современному уравнению Бернулли, был опубликован в 1738 году Даниилом Бернулли[K 1]. В современном виде интеграл был опубликован Иоганном Бернулли в 1743 году[11] для случая несжимаемой жидкости, а для некоторых случаев течений сжимаемой жидкости – Эйлером в 1757 году[12].

Интеграл Бернулли в несжимаемой жидкости[править | править код]

Для стационарного течения несжимаемой жидкости уравнение Бернулли может быть получено как следствие закона сохранения энергии. Закон Бернулли утверждает, что величина сохраняет постоянное значение вдоль линии тока:

Здесь

– плотность жидкости; – скорость потока; – высота; – давление; – ускорение свободного падения.

Элементарный вывод уравнения Бернулли из закона сохранения энергии

Элементарный вывод уравнения Бернулли из закона сохранения энергии приведён, например, в учебнике Д. В. Сивухина[13]. Рассматривается стационарное движение жидкости вдоль линии тока, изображённое на рисунке. Слева на объем жидкости, первоначально заключённый между двумя сечениями и , действует сила , а справа – противоположного направления сила . Скорость и давление в сечениях 1 и 2, а также их площади обозначены нижними индексами 1 и 2. За бесконечно малое время левая граница этого объёма жидкости сместилась на малое расстояние , а правая – на расстояние . Работа, совершённая силами давления, равна:

В начале интервала времени объем жидкости, заключённый между двумя поверхностями и , состоит из левого голубого элемента и средней синей части, в конце этого интервала сместившийся объём состоит из средней синей части и правого голубого элемента. Так как течение стационарное, вклад синего фрагмента в энергию и массу обсуждаемого объёма жидкости не меняется, а сохранение массы позволяет заключить, что масса левого голубого элемента равна массе правого голубого элемента: Поэтому работа сил, выражение для которой можно преобразовать к виду: равна изменению энергии, равному, в свою очередь, разности энергий правого голубого элемента и левого голубого элемента .

Для несжимаемой жидкости можно, во-первых, в выражении для работы положить и, во-вторых, в выражении для энергии элемента жидкости ограничиться кинетической и потенциальной энергией: После этого равенство даёт: , или .

Константа в правой части (может различаться для различных линий тока) иногда называется полным давлением[2]. Могут также использоваться термины «весовое давление» , «статическое давление» и «динамическое давление» . По словам Д. В. Сивухина[13], нерациональность этих понятий отмечалась многими физиками.

Размерность всех слагаемых – единица энергии на единицу объёма. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Третье слагаемое по своему происхождению является работой сил давления (см. приведённый выше вывод уравнения Бернулли), но в гидравлике может называться «энергией давления» и частью потенциальной энергии[14]).

Вывод формулы Торричелли из закона Бернулли[править | править код]

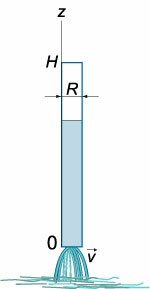
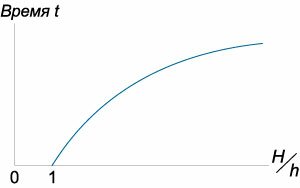
Иллюстрация формулы Торричелли

В применении к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда закон Бернулли даёт равенство полных давлений на свободной поверхности жидкости и на выходе из отверстия:

где

– высота столба жидкости в сосуде, отсчитанная от уровня отверстия, – скорость истечения жидкости, – атмосферное давление.

Отсюда: . Это – формула Торричелли. Она показывает, что при истечении жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты . Или, если истекающую из малого отверстия в сосуде струю направить вверх, в верхней точке (в пренебрежении потерями) струя достигнет уровня свободной поверхности в сосуде[15].

Другие проявления и применения закона Бернулли[править | править код]

Закон Бернулли объясняет эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем в широкой части

Приближение несжимаемой жидкости, а с ним и закон Бернулли справедливы и для ламинарных течений газа, если только скорости течения малы по сравнению со скоростью звука[16].

Вдоль горизонтальной трубы координата постоянна и уравнение Бернулли принимает вид . Отсюда следует, что при уменьшении сечения потока из-за возрастания скорости давление падает. Эффект понижения давления при увеличении скорости потока лежит в основе работы расходомера Вентури[17] и струйного насоса[1].

Закон Бернулли объясняет, почему суда, движущиеся параллельным курсом, могут притягиваться друг к другу (например, такой инцидент произошёл с лайнером «Олимпик»)[18].

Применение в гидравлике[править | править код]

Последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины – гидравлики. Для технических приложений часто уравнение Бернулли записывается в виде, в котором все члены разделены на «удельный вес» :

где имеющие размерность длины члены в этом уравнении могут иметь следующие названия:

– гидравлическая высота[4] или напор[19], – нивелирная высота[4], – пьезометрическая высота[4] или (в сумме с нивелирной высотой) гидростатический напор[19], – скоростная высота[4] или скоростной напор[19].

Закон Бернулли справедлив только для идеальных жидкостей, в которых отсутствуют потери на вязкое трение. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, приближённо учитывающих различные «гидравлические потери напора»[19].

Интеграл Бернулли в баротропных течениях[править | править код]

Уравнение Бернулли может быть выведено и из уравнения движения жидкости[K 2][K 3]. При этом течение предполагается стационарным и баротропным. Последнее означает, что плотность жидкости или газа не обязательно постоянна (как у предполагавшейся ранее несжимаемой жидкости), но является функцией только давления: , что позволяет ввести функцию давления[22] В этих предположениях величина

постоянна вдоль любой линии тока и любой вихревой линии. Соотношение справедливо для течения в любом потенциальном поле, при этом заменяется на потенциал массовой силы .

Вывод интеграла Бернулли для баротропного течения

Для безвихревых баротропных течений, скорость которых может быть выражена в виде градиента потенциала скорости , интеграл Бернулли в виде [K 4] сохраняется также в нестационарных течениях, причём постоянная в правой части имеет одинаковое значение для всего течения[25].

Формула Сен-Венана – Ванцеля[править | править код]

Если в течении совершенного газа выполняется адиабатический закон[26]

то уравнение Бернулли выражается так[27] (вкладом от силы тяжести обычно можно пренебречь):

вдоль линии тока или вихревой линии. Здесь – показатель адиабаты газа, выражающийся через теплоёмкости при постоянном давлении и при постоянном объёме, – давление и плотность газа, – условно выбранные постоянные (одинаковые для всего течения) значения давления и плотности.

С помощью полученной формулы находят скорость газа, вытекающего из сосуда с высоким давлением через малое отверстие. Удобно давление и плотность газа в сосуде, скорость газа в котором равна нулю, принять за тогда скорость истечения выражается через внешнее давление по формуле Сен-Венана – Ванцеля[28]:

Термодинамика закона Бернулли[править | править код]

Из термодинамики следует, что вдоль линии тока любого стационарного течения идеальной жидкости

где – энтальпия единицы массы, – гравитационный потенциал (равный для однородной силы тяжести), – энтропия единицы массы.

Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений

Интеграл Бернулли применяют в инженерных расчётах, в том числе для сред, весьма далёких по своим свойствам от идеального газа, например для водяного пара, используемого в качестве теплоносителя в паровых турбин. При этом могут использоваться так называемые диаграммы Молье, представляющих удельную энтальпию (по оси ординат) как функцию удельной энтропии (по оси абсцисс) и например давления (или температуры) в виде семейства изобар (изотерм). В этом случае последовательность состояний вдоль линии тока лежат на некоторой вертикальной линии (). Длина отрезка этой линии, отсекаемого двумя изобарами, соответствующего начальному и конечному давлению теплоносителя, равен половине изменения квадрата скорости[31].

Обобщения интеграла Бернулли[править | править код]

Интеграл Бернулли также сохраняется при переходе потока через фронт ударной волны, в системе отсчета, в которой ударная волна покоится[32]. Однако при таком переходе энтропия среды не остаётся постоянной (возрастает), поэтому соотношение Бернулли является лишь одним из трёх соотношений Гюгонио, наряду с законами сохранения массы и импульса, связывающих состояние среды за фронтом с состоянием среды перед фронтом и со скоростью ударной волны.

Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений[33]), в магнитной гидродинамике[34], феррогидродинамике[35]. В релятивистской гидродинамике, когда скорости течения становятся сравнимыми со скоростью света , интеграл формулируется в терминах релятивистски инвариантных[36] удельной энтальпии и удельной энтропии[37].

Комментарии[править | править код]

1. ↑ В записи Д.Бернулли в явном виде не фигурировало внутреннее давление в жидкости[8][9][10].
2. ↑ «…[Вывод теоремы Бернулли из уравнения энергии] обедняет содержание теоремы Бернулли … Интеграл Бернулли, вообще говоря, не зависит от уравнения энергии, хотя действительно совпадает с ним для изоэнтропического и адиабатического движения совершенного газа»[20].
3. ↑ «Два … пути получения уравнения Бернулли не эквивалентны. При энергетическом выводе нет необходимости в предположении об изэнтропичности течения. При интегрировании уравнения движения интегралы Бернулли получаются не только вдоль линий тока, но и вдоль вихревых линий»[21].
4. ↑ В русскоязычной литературе интеграл Бернулли для потенциальных течений несжимаемой или баротропной жидкости известен как интеграл Коши – Лагранжа[25]

Примечания[править | править код]

1. ↑ 1 2 Ландсберг Г. С. Закон Бернулли, 1985.
2. ↑ 1 2 3 4 Вишневецкий С. Л. Бернулли уравнение, 1988.
3. ↑ Титьенс О., Прандтль Л. Гидро- и аэромеханика, 1933.
4. ↑ 1 2 3 4 5 Лойцянский Л. Г. Механика жидкости и газа, 2003, §24. Теорема Бернулли.
5. ↑ Милн-Томсон Л. М. Теоретическая гидродинамика, 1964.
6. ↑ Седов Л. И. Механика сплошной среды, 1970.
7. ↑ Чёрный Г. Г. Газовая динамика, 1988.
8. ↑ Трусделл К. Очерки по истории механики, 2002.
9. ↑ Михайлов Г. К., 1999, с. 17.
10. ↑ Darrigol O. A history of hydrodynamics, 2005, с. 9.
11. ↑ Трусделл К. Очерки по истории механики, 2002, с. 255, 257.
12. ↑ Euler L. Continuation des recherches, 1755 (1757), с. 331.
13. ↑ 1 2 Сивухин Д. В. Механика, 1989, §94. Стационарное движение идеальной жидкости. Уравнение Бернулли.
14. ↑ Чугаев Р. Р. Гидравлика. – Л.: Энергия, 1975. – 600 с.
15. ↑ Сивухин Д. В. Механика, 1989, §95. Примеры на применение уравнения Бернулли. Формула Торричелли.
16. ↑ Сивухин Д. В. Механика, 1989, §94, формула (94.6).
17. ↑ Молоканов Ю. К. Процессы и аппараты нефтегазопереработки. – М.: Химия, 1980. – С. 60. – 408 с.
18. ↑ Я. И. Перельман. Отчего притягиваются корабли?. Дата обращения: 27 декабря 2018.
19. ↑ 1 2 3 4 5 Напор, 1992.
20. ↑ Бэтчелор Дж. Введение в динамику жидкости, 1973, Примечание Г. Ю. Степанова, с. 208.
21. ↑ Гольдштейн Р. В., Городцов В. А. Механика сплошных сред, 2000, с. 104.
22. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (9).
23. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (7).
24. ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VIII. §2, уравнение (2.1).
25. ↑ 1 2 Лойцянский Л. Г. Механика жидкости и газа, 2003, §42. Интеграл Лагранжа – Коши.
26. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (29).
27. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (30).
28. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (31).
29. ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (2.4).
30. ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VII. §2. Функция давления.
31. ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 446.
32. ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, §85.
33. ↑ Голубкин В. Н., Сизых Г. Б. О некоторых общих свойствах плоскопараллельных течений вязкой жидкости // Известия АН СССР, серия Механика жидкости и газа : журнал. – 1987. – № 3. – С. 176-178. – doi:10.1007/BF01051932.
34. ↑ Куликовский А. Г., Любимов Г. А. Магнитная гидродинамика. – М.: Физматлит, 1962. – С. 54. – 248 с.
35. ↑ Розенцвейг Р. Феррогидродинамика / Пер. с англ. под ред. В. В. Гогосова. – М.: Мир, 1989. – С. 136. – 359 с. – ISBN 5-03-000997-3.
36. ↑ Зубарев Д. Н., Релятивистская термодинамика, 1994.
37. ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (134.11).

Литература[править | править код]

• Бэтчелор Дж. Введение в динамику жидкости / Пер. с англ. под ред. Г. Ю. Степанова. – М.: Мир, 1973. – 760 с.
• Вишневецкий С. Л. Бернулли уравнение // Физическая энциклопедия / Гл. ред. А. М. Прохоров. – М.: Советская энциклопедия, 1988. – Т. 1: Ааронова-Бома эффект – Длинные линии. – С. 187. – 704 с.
• Гольдштейн Р. В., Городцов В. А. Механика сплошных сред. Часть 1. – М.: Физматлит, 2000. – 256 с. – ISBN 5-02-015555-1.
• Зубарев, Д. Н. Релятивистская термодинамика // Физическая энциклопедия / Гл. ред. А. М. Прохоров. – М.: Большая российская энциклопедия, 1994. – Т. 4: Пойнтинга-Робертсона эффект – Стримеры. – С. 333-334. – 704 с. – ISBN 5-85270-087-8.
• Ландау, Л. Д., Лифшиц, Е. М. Гидродинамика. – Издание 5-е, стереотипное. – М.: Физматлит, 2001. – 736 с. – («Теоретическая физика», том VI). – ISBN 5-9221-0121-8.
• Лойцянский Л. Г. Механика жидкости и газа. – М.: Дрофа, 2003. – 842 с. – ISBN 5-7107-6327-6.
• Милн-Томсон Л. М. Теоретическая гидродинамика. – М.: Мир, 1964. – 656 с.
• Михайлов Г. К. Становление гидравлики и гидродинамики в трудах петербургских академиков (XVIII) // Известия Академии наук, серия Механика жидкости и газа : журнал. – 1999. – Вып. 6. – С. 7-25.
• Напор // Физическая энциклопедия / Гл. ред. А. М. Прохоров. – М.: Большая российская энциклопедия, 1992. – Т. 3: Магнитоплазменный компрессор – Пойнтинга теорема. – С. 242. – 672 с. – ISBN 5-85270-019-3.
• Поль Р. В. Механика, акустика и учение о теплоте. – Рипол Классик, 2013. – 490 с. – ISBN 5458431251, 9785458431255.
• Седов Л. И. Механика сплошной среды. – М.: Наука, 1970. – Т. 2. – 568 с.
• Сивухин Д. В. Общий курс физики. – Издание 3-е, исправленное и дополненное. – М.: Наука, 1989. – Т. I. Механика. – 576 с. – ISBN 5-02-014054-6.
• Титьенс О., Прандтль Л. Гидро- и аэромеханика. – М.-Л.: ГТТИ, 1933. – Т. 1. – 224 с.
• Трусделл К. Очерки по истории механики. – М. – Ижевск: Институт компьютерных исследований, 2002. – 316 с. – ISBN 5-93972-192-3.
• Фабер Т. Е. Гидроаэродинамика / Пер. с англ. под ред. А. А. Павельева. – М.: Постмаркет, 2001. – 560 с. – ISBN 5-901095-04-9.
• Чёрный Г. Г. Газовая динамика. – М.: Наука, 1988. – 424 с. – ISBN 5-02-013814-2.
• §182. Закон Бернулли // Элементарный учебник физики / Под ред. Г. С. Ландсберга. – М.: Наука, 1985. – Т. 1. Механика. Теплота. Молекулярная физика.
• Darrigol O. Worlds of flow. A history of hydrodynamics from the Bernoullis to Prandtl. – Oxford: Oxford University Press, 2005. – 356 с. – ISBN 978-0-19-856843-8.
• Euler L. Continuation des recherches sur la théorie du mouvement des fluides // Mémoires de l’Académie royale des sciences et belles lettres. – Berlin, 1755 (1757). – Т. 11. – С. 316-361.
• Truesdell, Clifford Ambrose. Rational fluid mechanics, 1687-1765. Editor’s duction to Euleri Opera omnia II 12 // Leonardi Euleri. Opera Omnia. – Lausanne: Auctoritate et Impensis, Societas Scientiarum Naturalium Helveticae, 1954. – Т. 12. – С. I-CXXV. – (II).

Ссылки[править | править код]

• Русский перевод трактата Даниила Бернулли, в котором впервые появляется интеграл (закон) Бернулли

Источник