Сообщающие сосуды в быту

Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа с. Киселёвка
Ульчского района Хабаровского края
Проектная работа
«Сообщающиеся сосуды в нашей жизни»
Автор проекта: Стрельников Александр, ученик 7 класса
Руководитель: Ойдуп Елена Баторовна,
учитель физики
с. Киселёвка
2019 год
Содержание
Введение……………………………………………………………….3
Теоретическая часть…………………………………………………4
Сообщающиеся сосуды……………………………………….4
Применение сообщающихся сосудов……………………….4
2.2.1. В природе……………………………………………….4
2.2.2. В медицине………………………………………………5
2.2.3. В быту……………………………………………………6
История создания фонтанов……………………………………7
Практическая часть……………………………………………………10
Изготовление фонтана………………………………………….10
Заключение……………………………………………………………..12
Список литературы…………………………………………………….13
Введение.
Актуальность.
При изучении темы «Сообщающиеся сосуды» на уроке физики учитель продемонстрировал опыт – вода наливается в сообщающиеся сосуды различных форм. По итогам демонстрации мы сделали вывод, что независимо от формы сосудов, жидкость устанавливается на одном уровне. К сообщающимся сосудам относятся нами известные лейка, чайник, сифон под раковиной, водопровод с водонапорной башней, а больше всего меня заинтересовал фонтан. Его устройство основано на принципе сообщающихся сосудов.
Проблемный вопрос: Можно ли в домашних условиях сделать сообщающиеся сосуды?
Гипотеза: Если я самостоятельно изготовлю сообщающиеся сосуды, то лучше пойму принцип их действия.
Цель моего проекта: создать сообщающиеся сосуды (фонтан) из подручных средств.
Задачи:
– изучить источники информации по теме работы;
– изучить свойства сообщающихся сосудов;
– показать широкое применение сообщающихся сосудов в быту, технике и природе.
Практическая значимость – полученные результаты помогут в изучении данной темы в школе, привлечет внимание школьников к этому физическому процессу.
Объект – сообщающиеся сосуды
Предмет – фонтан.
Методы:
– поиск и изучение литературы
-анализ и систематизация полученной информации;
– обобщение полученной (в ходе исследования) информации.
Ожидаемый результат: изготовлен фонтан.
2. Теоретическая часть.
2.1. Сообщающиеся сосуды.
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха на воздух над жидкостью одинаково). Это можно обосновать следующим образом. Жидкость покоится, не перемещаясь из одного сосуда в другой, значит, давление в обоих сосудов на любом уровне одинаковое. Жидкость в обоих сосудах одна и та же, т.е. имеет одинаковую плотность. Следовательно, должны быть одинаковы и её высоты. Когда мы поднимаем один сосуд или доливаем в него жидкость, то давление в нём увеличивается и жидкость перемешается в другой сосуд до тех пор, пока давления не станут одинаковыми. Примером сообщающихся сосуд могут служить шлюзы, которые воздвигают для прохода судов в обход плотин гидроэлектростанций, или каналы, соединяющие реки. Если в один из сообщающихся сосудов налить жидкость одной плотности, а во второй- другой, то при равновесии уровни этих жидкостей не будут одинаковыми. И это понятно. Мы ведь знаем, что давление жидкости на дно сосуда прямо пропорционально высоте столба и плотности жидкости. А в этом случае плотность жидкостей различна, поэтому высоты столбов этих жидкостей будут различны. При равенстве давлений высота столба жидкости с большой плотностью будет меньше высоты столба жидкости с меньшей плотностью.
2.2. Применение сообщающихся сосудов.
2.2.1. В природе.
Все моря и океаны мира являются сообщающимися сосудами. Ведь они соединены между собой проливами (рис.1)
Акведук – это водяной желоб, поддерживаемый мостами. Вода бежит по акведуку над впадинами, холмами под действием собственного веса – от горных потоков к городам, расположенных в долине (рис. 2)
Артезианская скважина. Такая скважина работает по принципу сообщающихся сосудов. Под слоем почвы в низких местах скапливается вода. После бурения скважины вода поднимается вверх до уровня верхних горизонтов грунтовых вод (рис. 3)
Кровеносно-сосудистая система человека или животного состоит из сообщающихся сосудов (рис. 4)


Рис. 1 Рис. 2


Рис. 3 Рис. 4
2.2.2. В медицине.
Капельница, разновидность клизмы (рис5)
Рис. 5
2.2.3.В быту.
Использование всех виде сифонов в бытовых устройствах, где используется вода (рис.6) 

Современный водопровод ( рис. 7)

Рис. 7
Поливка из самодельного устройства: бак, стоящий на возвышении, заполняют водой и подключают ( рис. 8)

Рис. 8
Система нагревания и охлаждения (радиатор и расширительный бачок)
(рис. 9)
Рис. 9
Шлюзовые камеры, разного рода доки на судоремонтных предприятиях, гидравлические домкраты, чернильцы – непроливашки, некоторые картриджи струйных принтеров (рис. 10)


Рис. 10
Водонапорная башня. Кроме уже упомянутых леек и чайников, вода в наши дома поступает именно благодаря этому закону. Как мы добываем чистую воду из-под земли? Выкачиваем насосом. Но нельзя же подключить по насосу к каждому крану и к каждой квартире. Поэтому придумали следующую Рис. 11
схему – воду накачивают в водонапорную башню, представляющую из себя, по сути, огромный бак на большой высоте. А оттуда по закону сообщающихся сосудов вода под давлением течет в наши дома и льется их кранов, стоит только их открыть
История создания фонтана.
Фонтан (от ит. fontana, от лат. Fontis- источник) –струя жидкости или газа, выбрасываемая под давлением. (Словарь иностранных слов. – М.: Русский язык, 1990).
Фонтан – это не просто бьющий источник воды, но и традиционное украшение городских парков и площадей – известен человечеству со времен древней Греции.
Первые фонтаны (VI в до н.э.) имели очень простое устройство, и совсем не были похожи на пышные фонтаны современности .
Постепенно греки начинали украшать их, обкладывать плиткой, строить статуи, добивались высоких струй.
Вслед за древними Греками, фонтаны начали строить в Риме фонтаны сооружались как источники питьевой воды и для того, чтобы освежить воздух в жару. Римляне значительно усовершенствовали устройство фонтанов. Для фонтанов римляне делали трубы из обожженной глины или свинца. В эпоху расцвета Рима, фонтан стал обязательным атрибутом всех богатых домов. Струи воды били изо рта красивых рыб или экзотических животных.
После падения древнего мира, фонтан вновь превращается лишь в источник воды. Возрождение фонтанов как искусства начинается лишь во времена Ренессанса. Наиболее известными являются фонтаны Версаля во Франции и Петергофа в России.
По первоначальному замыслу Петра Первого в Петергофе в честь победы над Швецией должен был быть создан фонтан с изображением Геракла, побеждающего Лернейскую гидру, но этот план не был осуществлён. К идее установки памятного фонтана вернулись в царствование императрицы Анны Иоанновны, когда в 1734 году шла подготовка к празднованию 25-летия Полтавской победы. Считается, что фигура Самсона появилась в связи с тем, что Полтавская битва состоялась в день Самсония Странноприимца. Лев же связывается со Швецией, так как именно этот символ присутствует на гербе страны и до наших дней.
За всю историю существования Петергофа перед Большим каскадом было три фонтана «Самсон». Но фонтан, который находится там на сегодняшний день создал Козловский Михаил Иванович.
Современным фонтанам придаётся декоративный характер, который усиливается электрической подсветкой и музыкой в вечерние часы.
Как правильно сконструировать фонтан, чтобы он хорошо служил людям? С античных времён сохранились работы греческого механика Герона Александрийского, жившего в I – II в. н.э., исследовавшего от чего зависит расход воды, необходимый для хорошей работы фонтана. Герон выяснил, что расход воды зависит от её уровня в водохранилище, от поперечного сечения канала и скорости воды в нём.
Практическая часть
Изготовление фонтана
Устройство фонтана основано на принципе сообщающихся сосудов.
Для изготовления фонтана я взял пластиковую бутылку емкостью 5 литров, сделал отверстие в крышке (рис.12). Вторым сосудом мне послужил пластмассовый тазик, который поставил на пол (рис. 13). Два сосуда соединил капроновыми трубками от медицинской системы переливания растворов. Верхний сосуд заполнил водой, а в нижнем сосуде, чтобы трубка стояла устойчиво, вдел в воронку и обложил камнями.
На высоте 50 см вода не переливалась, поэтому сосуд поднял еще на 50 см. (рис. 14). Вывод: чем больше разница высот, тем сильнее давление и выше струя фонтана.
Так же попробовал 2 трубки с разным диаметром. Из трубки с меньшим диаметров струя била выше. Вывод: чем меньше диаметр, тем выше бьет фонтан.
Когда вся вода из верхнего сосуда перельется в сосуд, стоящий ниже, фонтан перестает действовать.



Рис. 12 Рис. 13


Рис. 14

Заключение
В ходе изучения материала различных источников, узнал, что сообщающихся сосудов нас окружают очень много; они встречаются в быту, природе, медицине. Из всех сообщающихся сосудов меня заинтересовало устройство фонтана.
Исследовав, от чего зависит высота струи фонтана, я пришел к выводу:
Струя фонтана бьет выше, если:
– выше уровень воды в водяном хранилище (сосуде с водой);
– меньше диаметр пластиковой трубки.
Я совершенствовал свои умения в оформлении презентации, учился отбирать нужную информацию из различных источников.
Список литературы:
Перышкин А.В. Физика. 7 кл. – 3-е изд.,доп. – М.: Дрофа, 2014-224с
https://www.mirfontanov.ru/fountain_history.html
https://kuznica.com/velikie-mastera/140-chudesnye-izobreteniya-gerona-aleksandrijskogo
https://www.mediaterra.ru/materials/inner/interior/fountains
15
Источник
Всем известно, что нужно сделать с чайником, чтобы из его носика полилась вода, – просто наклонить. А вот вопрос, можно ли перевести корабль через гору в море или другой водоем, вызовет у нас сомнение. Чтобы ответить на него, сначала следует узнать, что из себя представляют сообщающиеся сосуды.

Закон сообщающихся сосудов
Сообщающиеся сосуды – это взаимодействующие друг с другом сосуды, которые имеют общее дно.
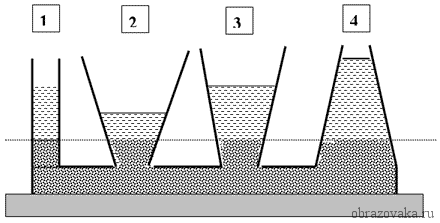
Рис. 1. Сообщающиеся сосуды
Закон сообщающихся сосудов гласит, что в таких сосудах, какую бы форму они не имели, поверхности однородных жидкостей в состоянии покоя находятся на одном уровне, то есть давление, оказываемое на стенки на любом горизонтальном уровне является одинаковым.
Если же в сосуде жидкости разные, то уровень выше в сосуде, в котором жидкость обладает меньшей плотностью. То есть, если в один сосуд налить жидкость, обладающую одной плотностью, а во второй – другой, то при равновесии их уровни не будут одинаковыми. Следовательно отсюда можно вывести формулу:
ρ1/ρ2=h2/h1
Где:
- ρ – плотность жидкости;
- h – высота столба.
Также для сообщающихся сосудов важной является формула:
p=gρh
Где:
- g – ускорение свободного падения;
- ρ – плотность жидкости (кг/куб.м);
- h – глубина (высота столба жидкости).
Этой формулой определяется давление жидкости на дно сосуда.
Древним римлянам было неизвестно определение сообщающихся сосудов, поэтому их акведуки – водопроводы занимали огромную протяженность над поверхностью земли и строились с равномерным уклоном вниз.
Свойства сообщающихся сосудов
В сообщающихся сосудах уровень жидкости одинаковый. Это происходит потому, что жидкость производит одинаковое давление на стенки сосуда. Достичь разного уровня однородной жидкости в сообщающихся сосудах можно с помощью перегородки между ними.
Перегородка перекроет сообщение между сосудами, и тогда можно в один из них долить жидкость, чтобы уровень изменился. В данной ситуации возникает напор – давление, производимое весом столба жидкости высотой, равной разности уровней. И если убрать перегородку, то именно это давление станет причиной тому, что жидкость будет перетекать в тот сосуд, где ее уровень ниже, до тех пор, пока уровни не станут одинаковыми.
В жизни очень часто можно встретить естественный напор. И таких примеров довольно много. Например, им обладает вода в горных реках, когда падает с высоты. Плотина также является примером естественного напора. Чем она выше, тем больше будет напор воды, поднятой плотиной.
Применение закона о сообщающихся сосудах
Принцип действия сообщающихся сосудов используется при сооружении фонтанов, водопроводов, шлюзов. Чайник и его носик тоже являются сообщающимися сосудами, так как вода, налитая в чайник, заполняет носик и всю остальную часть до одинаковой высоты. Применение свойств таких сосудов, могут даже помочь провести корабль через гору. И для этого как раз понадобиться шлюз. Шлюз – это лифт для судов. Если водное пространство перегорожено плотиной, то уровень воды в водохранилище выше, чем в реке ниже по течению. И чтобы добраться до этого уровня, судно должно зайти в шлюз, который отгорожен двумя водными непроницаемыми воротами. Когда шлюз полностью заполняется водой, судно выходит из шлюза и продолжает свой путь (уровень воды в шлюзе и водохранилище выравнивается по закону сообщающихся сосудов).

Рис. 2. Шлюз
Что мы узнали?
Из этой темы по физики за 7 класс можно ясно понять, какие сосуды называются сообщающимися. Ими могут называться лишь те сосуды, обладающие общим дном, где жидкость может свободно перетекать из одного сосуда в другой. Также сообщающиеся сосуды играют огромную роль в нашей повседневной жизни, облегчая ее и помогая выходить из трудных ситуаций. Принципы сообщающихся сосудов лежат в основе различных чайников, кофейников, водомерных стекол на паровых котлах.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-

Алика Квегмайр
10/10

Яна Василькова
10/10

Елена Куренкова
9/10

Мария Егорова
8/10

Тимофей Черный
10/10

Максим Скарнович
10/10

Люба Музыченко
10/10

Владимир Шитов
9/10

Константин Никитич
9/10

Катя Пу
10/10
Оценка доклада
Средняя оценка: 4.2. Всего получено оценок: 836.
Источник

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики

P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.

Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов

Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов

На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.

В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов

Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.

Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.

Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
