Сообщающиеся сосуды площадь поршня

Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
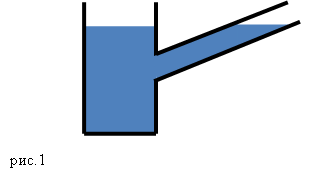
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
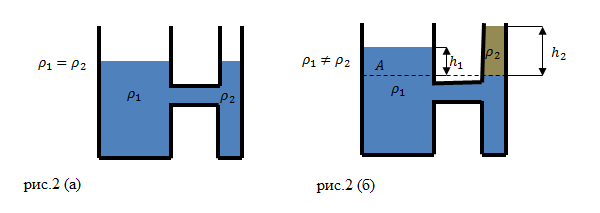
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
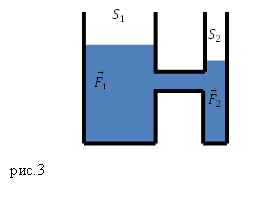
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
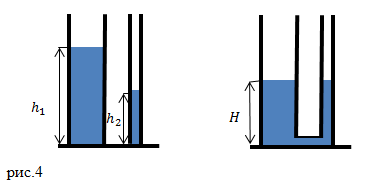
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.
Источник

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики

P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.

Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов

Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов

На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.

В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов

Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.

Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.

Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
№ 16611
Два высоких цилиндра, сообщающихся с атмосферой, соединены одинаковыми тонкими трубками AB и CD и заполнены водой (рис. ). Расстояние между трубками равно h0 = 1 м. Температуры воды в цилиндрах поддерживаются постоянными и равными t1 = 100 °С и t2 = 40 °С. Плотность воды зависит от температуры по закону ρ = ρ0·[1 – β·(t – t0)], где t0 – комнатная температура, ρ0 = 1,0×103 кг/м3 – плотность воды при комнатной температуре, коэффициент β = 2,1×10-6 град-1. В такой системе возникает круговая циркуляция воды по трубкам между цилиндрами. Известно, что масса воды, перетекающей по трубкам в единицу времени, пропорциональна разности давлений на их концах. Определите разность давлений ∆pAB и ∆pCD на концах трубок AB и CD.
№ 16705
В двух вертикальных сообщающихся цилиндрах (рис. ) под поршнями массами 2m и m находится один моль идеального одноатомного газа. Над поршнями – вакуум. На рисунке показаны геометрические размеры: S – площадь поршня, V ΄ – объем трубы, соединяющей сосуды. Поршень 2m закреплен, а поршень m свободен. Затем поршень 2m освобождают. Оба поршня начинают перемещаться без трения. Удар поршня m о верхнюю крышку цилиндра происходит абсолютно упруго. Найдите максимально большое отношение Tк/T0, которое можно достигнуть, изменяя расстояние b (Tк – конечная равновесная температура газа, а T0 – начальная). Принять, что стенки цилиндров и поршни теплом с газом не обмениваются.
№ 16936
Три сообщающихся сосуда с водой, центры которых находятся на одинаковом расстоянии a друг от друга, прикрыты поршнями одинаковой толщины, сделанными из одного и того же материала (рис.). К поршням прикреплены вертикальные одинаковые штоки, которые шарнирно соединены со стержнем AB. В какой точке стержня можно прикрепить к нему груз, чтобы в положении равновесия стержень оставался горизонтальным, если массы стержня и штоков пренебрежимо малы по сравнению с массами поршней и груза? Диаметры сосудов указаны на рисунке.
№ 16954
Форма сообщающихся сосудов показана на рисунке. Куда потечет вода по трубке, соединяющей сосуды, если нагреть воду в одном из сосудов?
№ 16984
U-образная трубка заполнена водой. Из одного колена воздух удален; давление воздуха в другом колене при температуре 20 °С равно атмосферному. Оба конца трубки запаяны. Разность между уровнями воды в коленах равна 15 м. Какой будет разность уровней воды в коленах, если трубку нагреть до 100 °С?
№ 17324
Два запаянных сообщающихся сосуда цилиндрической формы разных диаметров частично заполнены водой (ртутью) (рис.). Воздух из сосудов откачан, так что над жидкостью имеются только ее пары. Как распределится количество жидкости в сосудах: а) на земле? б) в невесомости?
№ 19205
Два сообщающихся цилиндрических сосуда высотой 5h, частично заполненные жидкостью плотностью ρ до высот 4h и 2h соответственно, смещены по вертикали на высоту 2h (рис.). Кран в трубке изначально закрыт. В правый сосуд добавляют жидкости плотностью 0,8ρ столько, что она занимает объем высотой 3h. Какой по высоте столб жидкости плотностью 0,8ρ останется в правом сосуде после того, как кран откроют и установится равновесие? Сверху все сосуды открыты. Объемом соединительной трубки можно пренебречь. Площади горизонтальных поперечных сечений сосудов одинаковые.
№ 19314
Вертикальные сообщающиеся сосуды с площадями сечения S и 2S соединены горизонтальным каналом площадью сечения S (см. рисунок). Сосуды перекрыты невесомыми подвижными поршнями, а весь объем под поршнями заполнен несжимаемой жидкостью. К поршням прикреплена крепкая нерастяжимая нить, перекинутая через блок. Ось блока начинают перемещать вверх с постоянной скоростью υ. С какой средней скоростью начинает двигаться жидкость в горизонтальном канале? Сами сосуды неподвижны, а поршни от жидкости не отрываются.
№ 19349
Имеются четыре одинаковых цилиндрических сосуда, в которые налито некоторое количество воды. Поверх воды в первый, второй и третий сосуды (рис.) аккуратно наливают слой масла толщиной h, 2h и 3h соответственно. На сколько изменится уровень жидкости в каждом сосуде по сравнению с первоначальным положением после установления равновесия? Известно, что при наливании масла вода ни из одного сосуда полностью маслом не вытесняется. Плотность масла ρ0, плотность воды ρ1 (ρ1 > ρ0).
№ 19600
Система из двух сообщающихся вертикальных цилиндров, заполненных жидкостью плотностью ρ, закрыта поршнями массами M1 и M2. В положении равновесия поршни находятся на одной высоте. Если на поршень массой M1 положить груз массой m, то поршень массой M2 поднимется после установления равновесия на высоту h относительно начального положения. На какую высоту относительно начального положения равновесия поднимется поршень массой M1, если груз массой m положить на поршень массой M2? Трения нет.
№ 19605
Два одинаковых сообщающихся сосуда наполнены жидкостью плотностью ρ0 и установлены на горизонтальном столе. В один из сосудов кладут маленький груз массой m и плотностью ρ. На сколько будут после этого отличаться силы давления сосудов на стол? Массой гибкой соединительной трубки с жидкостью можно пренебречь.
№ 19707
В два одинаковых сообщающихся сосуда налита вода (см. рисунок). В один их них кладут ледяной шарик объёмом V = 100 см3, который через небольшое время, после установления уровня воды в сосудах, оказался погруженным в воду ровно наполовину. Какая масса воды перетекла при этом во второй сосуд, и какая перетечёт потом, в процессе таяния льда? Плотность воды ρв = 1000 кг/м3, плотность льда ρл = 900 кг/м3.
№ 19948
В сообщающиеся сосуды налита вода. Площадь дна правого сосуда S = 100 см2, площадь дна левого — в три раза больше. Первоначально расстояние от поверхности воды до краев сосудов составляет H = 20 см. В сосуды медленно доливают жидкости: в левый воду, а в правый — масло. При этом за час в сосуды поступает V = 400 см3 воды и V = 400 см3 масла, жидкости не смешиваются. Через какое время жидкость начнет выливаться через край? Плотность воды ρ = 1 г/см3, плотность масла в 2 раза меньше, сосуды глубокие.
№ 20028
2. Имеются два цилиндрических сообщающихся сосуда, левый накрыт сверху легким поршнем (см. рис.). Площадь сечения левого сосуда равна 400 см2, площадь правого в два раза больше. Как поменяется положение поршня, если на него положить деревянный брусок массы 600 г, и такой же брусок запустить плавать в правый сосуд? В эксперименте вода из системы не выливается. Плотность воды 1 г/см3.
№ 20038
На рисунке изображены сообщающиеся сосуды с площадями сечения S1, S2 = 2S1 и рычаг с плечами l1, l2 = 3l1. Поршень в левом сосуде привязан веревкой к левому концу рычага. В правом сосуде на поршне находится гном массы M = 0,5 кг. В левом на поршне лежит груз такой же массы. С какой силой F гном тянет за веревку, привязанную к правому концу рычага, если вся конструкция пребывает в равновесии? Поршни находятся на одинаковой высоте, и их массой можно пренебречь.
№ 20075
Агрегат состоит из сообщающихся сосудов А и Б, и легкого поршня П, который может двигаться вертикально, не нарушая герметичность Агрегата. В сосуды и внутрь поршня Агрегата налита вода (см. рис.), система находится в равновесии. Насколько сдвинется поршень, если в сосуд А и внутрь поршня П аккуратно долить по 3 килограмма масла? Известно, что масло не выльется из сосуда А. Площади дна сосудов А и Б равны S = 200 см2, площадь поршня Sп = 300 см2. Плотность масла 0,8 г/см3, воды 1 г/см3.
№ 20167
5. Два сообщающихся сосуда, площади дна которых S и 2S, соединены трубкой L с большим резервуаром воды R. На воду в каждый сосуд положили по невесомому поршню, плотно прилегающему к стенкам. Первый поршень отвели на Δx вверх, второй на Δx вниз, и закрепили. Затем к поршням подсоединили систему нитей и блоков (см. рис.). На поршни положили грузы массами m и 2m, за нить потянули с силой T = mg/2. Поршни отпустили, и оказалось, что в начальный момент оба они поехали вниз. В какую сторону поехали бы поршни, если бы нить тянули с силой m·g? Нити нерастяжимы, блоки невесомы, трением пренебречь. При движении воды по трубке, уровень воды в резервуаре R практически не изменяется.
№ 20349
5. В высокие стеклянные сообщающиеся сосуды с металлическим дном на расстоянии 2 и 4 см от дна встроены горизонтальные проволочные сетки. Сетки, находящиеся на одном уровне, соединены проводами А и В. В систему залили ртуть до уровня 5 см. Затем в левый сосуд залили 5 см жидкого изолятора (его плотность меньше чем у ртути на Δρ), а сверху – 1 см еще более легкой жидкости с удельным сопротивлением в k раз больше, чем у ртути. Поверх жидкости поместили легкие проводящие поршни. Система пришла в равновесие, при этом ртуть в правом сосуде достигла уровня 7 см. К дну сосудов и поршням подключили батарейку (см. рис.: серым изображены обе проводящие жидкости, белым – изолятор). На левый поршень собираются ставить груз. Найдите электрическое сопротивление системы в зависимости от массы груза; постройте график этой зависимости. Плотность ртути ρ, ее удельное сопротивление r, площадь дна обоих сосудов S. Сопротивлением проводов и поршней, трением и тепловым расширением ртути пренебречь. Объем соединяющей сосуды трубки мал.
№ 20634
Изогнутая трубка состоит из одного горизонтального колена и двух вертикальных колен. Трубка укреплена на платформе, вращающейся с постоянной угловой скоростью вокруг вертикальной оси (рис.). Вертикальные колена находятся на расстояниях R и 3R от оси вращения. Установившаяся разность уровней (по высоте) налитой в трубку жидкости в вертикальных коленах равна H. Найдите угловую скорость вращения платформы. Диаметр трубки значительно меньше ее длины.
Источник
