Сообщающиеся сосуды с сосудом с газом

Закон сообщающихся сосудов

Сообщающиеся сосуды – это взаимодействующие друг с другом сосуды, которые имеют общее дно.

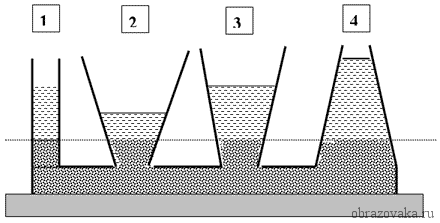
Рис. 1. Сообщающиеся сосуды

Закон сообщающихся сосудов гласит, что в таких сосудах, какую бы форму они не имели, поверхности однородных жидкостей в состоянии покоя находятся на одном уровне, то есть давление, оказываемое на стенки на любом горизонтальном уровне является одинаковым.

Если же в сосуде жидкости разные, то уровень выше в сосуде, в котором жидкость обладает меньшей плотностью. То есть, если в один сосуд налить жидкость, обладающую одной плотностью, а во второй – другой, то при равновесии их уровни не будут одинаковыми. Следовательно отсюда можно вывести формулу:

ρ1/ρ2=h2/h1

Где:

• ρ – плотность жидкости;
• h – высота столба.

Также для сообщающихся сосудов важной является формула:

p=gρh

Где:

• g – ускорение свободного падения;
• ρ – плотность жидкости (кг/куб.м);
• h – глубина (высота столба жидкости).

Этой формулой определяется давление жидкости на дно сосуда.

Свойства сообщающихся сосудов

В сообщающихся сосудах уровень жидкости одинаковый. Это происходит потому, что жидкость производит одинаковое давление на стенки сосуда. Достичь разного уровня однородной жидкости в сообщающихся сосудах можно с помощью перегородки между ними.

Перегородка перекроет сообщение между сосудами, и тогда можно в один из них долить жидкость, чтобы уровень изменился. В данной ситуации возникает напор – давление, производимое весом столба жидкости высотой, равной разности уровней. И если убрать перегородку, то именно это давление станет причиной тому, что жидкость будет перетекать в тот сосуд, где ее уровень ниже, до тех пор, пока уровни не станут одинаковыми.

Применение закона о сообщающихся сосудах

Принцип действия сообщающихся сосудов используется при сооружении фонтанов, водопроводов, шлюзов. Чайник и его носик тоже являются сообщающимися сосудами, так как вода, налитая в чайник, заполняет носик и всю остальную часть до одинаковой высоты. Применение свойств таких сосудов, могут даже помочь провести корабль через гору. И для этого как раз понадобиться шлюз. Шлюз – это лифт для судов. Если водное пространство перегорожено плотиной, то уровень воды в водохранилище выше, чем в реке ниже по течению. И чтобы добраться до этого уровня, судно должно зайти в шлюз, который отгорожен двумя водными непроницаемыми воротами. Когда шлюз полностью заполняется водой, судно выходит из шлюза и продолжает свой путь (уровень воды в шлюзе и водохранилище выравнивается по закону сообщающихся сосудов).

Рис. 2. Шлюз

Тест по теме

Статьи

Основное общее образование

Линия УМК А. В. Перышкина. Физика (7-9)

Физика

1.5. Гидростатика

Давление. Сила давления

Давление равно отношению силы давления к площади. Это универсальное определение относится к твердым телам, жидкости, газу.

Способы увеличения давления: увеличить силу; уменьшить площадь. Давление в твердых телах передается в том же направлении, в котором действует сила. При решении задач (например, тело на наклонной плоскости) рассматриваются проекции сил — давление тела на плоскость и реакция опоры — на оси координат. Направление движения тела, при действии несколкиз сил, не совпадает с направлением силы давления на тело.

Гидростатика. Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково. Это связано с подвижностью молекул в жидком и газообразном состояниях.

Давление столба жидкости:

(ро же аш), где ρ — плотность жидкости, g — ускорение свободного падения.
h – высота столба жидкости или глубина, на котороей измеряется давление.

Сила давления: F = p S . Используя две формулы, находим силу давления на дно сосуда, на боковую грань аквариума и т.п. Экзаменационные задачи на эту тему простые; вычисляйте всё в системе СИ.

Гидростатический парадокс (следствие закона Паскаля): давление на дно сосуда определяется только высотой столба жидкости. И не только на дно, но и вообще на данной глуибне. Независимо от фомы сосуда и его размеров (см. формулу выше).

Поэтому в трех сосудах давление на дно одинаково.

Но сила давления разная — не путаем понятия!

Сообщающиеся сосуды

Сообщающиеся сосуды – сосуды, соединенные между собой (трубкой) или имеющие общее дно.

Уровень жидкости в сообщающихся сосудах располагается горизонтально, если:

• поверхности жидкости открыты;

• в сосуды налита однородная жидкость;

• ни один из сосудов не является капилляром;

• в жидкостях нет пузырьков с воздухом.

Давление столбов жидкости на одном горизонтальном уровне одинаково:

Гидравлический пресс – простой механизм, дающий выигрыш в силе. Он представляет собой сообщающиеся сосуды разного сечения. В основе его действия лежит закон Паскаля.

Внешняя сила, действующая на малый поршень, совершает работу. Давление в жидкости одинаково. (Высота столбов жидкостей в цилиндрах пресса меняется, но в задачах это не учитывается.
Такой пресс может работать в любом положении и в невесомости.)

Сила давления жидкости, действующая на большой поршень совершает полезную работу. Из меньшего цилиндра в больший перемещается некоторый объем жидкости — при этом перемещение меньшего поршня больше. Выигрыш в силе аналогичен действию рычага. Затрачиваемая и совершаемая работы одинаковы (если КПД 100%).

Источник

II. Молекулярная физика

Тестирование онлайн

Давление

Это физическая скалярная величина, которая определяется по формуле

Атмосферное давление

Атмосфера — это воздушная оболочка Земли, которая удерживается гравитационными силами. Атмосфера имеет вес и давит на все тела на Земле. Давление атмосферы составляет около 760 мм.рт.ст. или 1 атм., или 101325Па. Миллиметр ртутного столба, атмосфера — это различные внесистемные единицы измерения давления. Атмосферное давление уменьшается на 1 мм.рт.ст. при поднятии над Землей на каждые 11м.

Что такое давление в 1 атм? Рукопожатие крепкого мужчины составляет 0,1 атм, удар боксера составляет несколько атмосферных единиц. Давление каблука-шпильки составляет 100 атмосфер. Если на ладонь положить гирю в 100 кг, то получим неравномерное давление в одну атмосферу, при погружении на 10 м под воду получим равномерное давление в 1 атмосферу. Равномерное давление легко переносится человеческим организмом. Нормальное атмосферное давление, которое действует на каждого человека, компенсируется внутренним давлением, поэтому его мы совершенно не замечаем, несмотря на то, что оно является достаточно существенным.

Закон Паскаля

Давление на жидкость или газ передается во всех направлениях одинаково.

Давление внутри жидкости (газа) на одной и той же глубине одинаково во всех направлениях (влево вправо, вниз и вверх!)

Гидростатическое давление

Это давления столбика жидкости на дно сосуда. Какая сила создает давление? Жидкость обладает весом, который давит на дно.

Давление жидкости на дно

Давление на дно сосуда не зависит от формы сосуда, но зависит от площади его дна. При этом сила давления на дно может быть и больше и меньше силы тяжести жидкости в сосуде. В этом заключается «гидростатический парадокс».

На стенку сосуда гидростатическое давление распределено неравномерно: у поверхности жидкости оно равно нулю (без учета атмосферного давления), внутри жидкости изменяется прямо пропорционально глубине и на уровне дна достигает значения

. Это переменное давление можно заменить средним давлением

Сообщающиеся сосуды

Это сосуды, которые имеют общий канал внизу.

Однородная жидкость устанавливается в сообщающихся сосудах на одном уровне независимо от формы сосудов, как видно на фотографии.

Разнородные жидкости устанавливаются в сообщающихся сосудах согласно формуле

Гидравлический пресс

Гидравлический пресс состоит из двух сообщающихся сосудов цилиндрической формы. В сосудах двигаются поршни с площадями S1 и S2. Цилиндры заполнены техническим маслом.

Объем жидкости, вытесненный малым поршнем поступает в большой цилиндр.

Гидравлический пресс дает выигрыш в силе во столько раз, во сколько площадь большего поршня больше площади меньшего. Выигрыша в работе гидравлический пресс не дает.

На практике вследствие наличия трения:

Давление не перпендикулярной к поверхности силы

Если сила направлена под углом к нормали (перпендикуляру), то давление определяется по формуле

Практическое применение

Газы и жидкости, находящиеся под давлением, нашли широкое применение в промышленной технике. Например, пневматический отбойный молоток. При помощи сжатого воздуха работают также двери в автобусах и метро, тормоза поездов и грузовых автомобилей.

Встречаются также механизмы, работающие при помощи сжатой жидкости. Они называются гидравлическими. Например, устройство гидравлического пресса.

Атмосферное давление открытие и измерение

Численное значение атмосферного давления было определено опытным путем в 1643 году итальянским ученым Э.Торричелли.

Стеклянную трубку длиной около метра, запаянную с одного конца, наполняют доверху ртутью. Затем, плотно закрыв отверстие пальцем, трубку переворачивают и опускают в чашу со ртутью, после чего палец убирают. Ртуть из трубки начинает выливаться, но не вся: остаётся «столб» » 76 см высотой, считая от уровня в чаше. Примечательно, что эта высота не зависит ни от длины трубки, ни от глубины её погружения.

Атмосферное давление уравновешивает гидростатическое давление столбика ртути. Согласно закону Паскаля давление атмосферы давит вверх на столбик ртути. А столбик ртути давит вниз своим весом. Ртуть перестает опускаться, когда эти давления одинаковые. Вычислив гидростатическое давление ртути известной высоты, определили давление атмосферы.

Трубка Торричелли с линейкой является простейшим барометром – прибором для измерения атмосферного давления

Для измерения атмосферного давления используют также барометр-анероид.

Поскольку атмосферное давление уменьшается по мере удаления от поверхности Земли, то шкалу анероида можно проградуировать в метрах. В этом случае он называется альтиметром.

Возникновение силы Архимеда

Пусть прямоугольный металлический брусок площадью основания S и высотой h лежит на дне сосуда, в который налита вода до высоты H, H>h. Как определить силу давления бруска на дно сосуда?

Возможны два случая! Пусть брусок неплотно прилегает ко дну сосуда, тогда снизу на брусок действует сила давления жидкости. Эта сила больше силы давления жидкости сверху, поэтому возникает сила Архимеда. Сила Архимеда — результат разницы силы гидростатического давления на нижнюю грань бруска и верхнюю грань, зависит от высоты бруска и площади основания.

Используем 2 закон Ньютона:

Рассмотрим второй возможный случай. Пусть брусок прилегает ко дну так плотно, что жидкость под него не подтекает. Снизу отсутствует давление жидкости, следовательно сила Архимеда равна нулю. Сверху же на брусок действует сила давления жидкости и атмосферы.

Используем 2 закон Ньютона для этого случая:

p — атмосферное давление,
p — гидростатическое давление столба жидкости высотой H-h.

Источник

Закон сообщающихся сосудов и его применение.

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.

Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.

Содержание статьи

Закон сообщающихся сосудов

Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:

Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.

Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.

Основное уравнение гидростатики

где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.

ρgh – сила тяжести (вес призмы).

Звучит уравнение так:

Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.

Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости

Доказательство закона сообщающихся сосудов

Возвращаемся к разговору про сообщающиеся сосуды.

Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.

Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.

Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики

если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.

Это давление можно определить следующим образом

где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2

P1 + ρ1gh1 = P2 + ρ2gh2

В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем

т.е. закон сообщающихся сосудов состоит в следующем.

В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.

Свойства сообщающихся сосудов

Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.

Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.

Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.

В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.

Приборы основанные на законе сообщающихся сосудов

На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.

Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.

В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.

Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.

Применение сообщающихся сосудов

Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.

Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.

Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.

Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.

В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.

Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.

В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.

Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.

Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.

Видео по теме

Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.

Источник