Сообщающиеся сосуды в вакууме

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики
P = P1 + ρgh
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.
Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
P = P1 + ρgh1
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
P = P2 + ρgh2
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем
ρ1h1 = ρ2h2
или
ρ1 / ρ2 = h2 / h1
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов
Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.
В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.
Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.
Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:
Источник
Рассмотрим сообщающиеся сосуды (рис. 1.6), заполненные не- смешивающимися жидкостями с разными удельными весами—у, и у2
(например, вода и ртуть, вода и масло). Давления на свободные поверхности жидкостей в сосудахр’ ир” соответственно.
Рис. 1.6. Сообщающиеся сосуды
Рассмотрим давления, создаваемые первой и второй жидкостями на поверхности а—а — границе раздела двух жидкостей. Давление первой жидкости: Ра6с = Р0+У А- Давление второй жидкости: Лбе =Ро + • Так как Давления равны, то р’0 + У А = Ро + ЧгК •
Для случая когда давления на свободные поверхности жидкостей
одинаковы р’0 = р», получим у А = УАг или — т.е. высоты раз-
К Y.
нородных жидкостей, покоящихся в сообщающихся сосудах, отсчитываемые от плоскости их раздела, обратно пропорциональны удельным весам этих жидкостей.
Для случая когда в сообщающихся сосудах находится одна и та же жидкость у = у2 и давления на свободные поверхности одинаковы Ро = Ро’ уровень жидкости в сосудах будет одинаков h= hr
На принципе сообщающихся сосудов основано действие жидкостных приборов, служащих для измерения избыточного давления и вакуума — пьезометров и вакуумметров.
Пьезометр (рис. 1.7) — это открытая сверху стеклянная трубка, присоединяемая к сосуду. Давление в точке присоединения в плоскости a-a равно рабс = раш +уh. Избыточное давление рнъЪ =Рабс~Рати = = Л™+УЛ-Лтм=Уй илиhp=^.
Следовательно, измерив высоту hp, можно определить избыточное давление в точке присоединения пьезометра. Высота hp =^~ называется пьезометрической высотой избыточного давления. ^
Рис. 1.7. Схема пьезометра, измеряющего избыточное давление
Если в плоскости присоединения прибора имеет место вакуум, то применяется вакуумметр (рис. 1.8).
Рис. 1.8. Схема жидкостного вакуумметра, измеряющего вакуумметрическое давление
Давление в плоскости п—п, совпадающей со свободной поверхностью жидкости в вакуумметре, равно рп = рятм. С другой стороны, давление рп можно определить по основному уравнению гидростатики (1.20) в виде
откуда следует
Раскрывая скобки, получим
Давление в плоскости присоединения вакуумметра т—т Po+Y^/W
Подставляя значение этого давления в предыдущее выражение, получимрабс + уАвак=раш, откуда /гвак = Разность в числителе представляет собой вакуум в плоскости т—т, следовательно, /гвак = Эта высота называется вакуумметрической высотой всасы- Y
вания.
Пьезометр и вакуумметр могут быть использованы для измерения избыточного давления и вакуума не только в плоскости своего присоединения, но и в любой другой плоскости, если измерить расстояния между этими плоскостями.
Жидкостные приборы, использующие воду, могут применяться для измерения избыточных давлений и вакуума в пределах 15…20 кПа. При избыточном давлении 19,62 кПа высота столба жидкости в пьезометре будет равна 2 м водяного столба. Поэтому чаще применяют ртутные приборы. Удельный вес ртути в 13,6 раза больше воды, значит, при одном и том же давлении высота h в 13,6 раза меньше, чем у водяного пьезометра.
Рассмотрим ртутные манометр и вакуумметр (рис. 1.9).
Рис. 1.9. Определение давления в сосуде с помощью ртутного дифманометра
Для плоскости б—б (см. рис. 1.9, а) имеем
Для вакуума (см. рис. 1.9, б) в плоскости б—б имеем
При более значительных давлениях используются пружинные манометры и вакуумметры (трубчатые или мембранные).
Вернемся к выделенному ранее выражению давления, имеющему вид
Представим его в другом виде
т.е. сумма величин z и для данной покоящейся жидкости — вели-
У
чина постоянная. Ее называют гидростатическим напором (#ст).
Величина ? называется геодезической высотой, или геодезическим напором, и измеряется от плоскости сравнения N— TV (рис. 1.10) до
данной точки или данной горизонтальной плоскости; — этопье-
У
зометрическая высота, или пьезометрический напор (соответствующий абсолютному давлению в точке подключения пьезометра).
Рис. 1.10. Схема к определению гидростатического напора
Выражение для статического напора означает, что в жидкости, находящейся в состоянии абсолютного равновесия, сумма геодезической и пьезометрической высот есть величина постоянная, равная гидростатическому напору. А уровни в пьезометрах, присоединенных к сосуду с покоящейся жидкостью в любом месте, установятся в одной горизонтальной плоскости на расстоянии, равном от плоскости сравнения.
Источник
ВАКУУМ
Акуум, который удавалось получить при помощи поршневого воздушного насоса, был невысок. Современная техника позволяет получить во много раз большие разрежения.
Как же будут изменяться свойства газов с увеличением разрежения? Начнем постепенно откачивать газ из какого – либо сосуда. Число молекул газа в нем будет постепенно уменьшаться. А раз уменьшится число ударов молекул о стенки, давление газа понизится. Будет уменьшаться и число столкновений молекул между собой, увеличится длина их свободного пробега. Все это будет отражаться на многих свойствах газа.
Величину вакуума обычно характеризуют давлением газа, оставшегося в откачиваемом объеме. Это давление выражают в миллиметрах ртутного столба. В настоящее время вакуумная техника позволяет достигнуть весьма высокой степени разрежения; теперь остаточное давление газа измеряется тысячными и миллионными долями миллиметра ртутного столба. Обозначая величину вакуума, для удобства десятичные дроби заменяют множителем 10 в отрицательной степени, который показывает число знаков после запятой; например 0,001 или 1/1000 обозначается 1 • 10~3; 0,000001—1 • 10~6 и т. д. При уменьшении давления в сотни и тысячи раз по сравнению с обычным давлением воздуха свойства газов не изменяются. Но когда давление газа уменьшается до сотых и тысячных долей миллиметра ртутного столба, в свойствах газов, находящихся в обычных лабораторных приборах или производственных аппаратах, происходят качественные изменения.
Обычное давление от высокого вакуума различают по длине свободного пробега молекул газа. При обычном дав
Лении длина свободного пробега молекул весьма невелика, например для воздуха она составляет около шести сотых микрона. Когда же вакуум достигает 0,01—0,001 (1 • 10 ”2— 1 • 10 -3) мм ртутного столба, длина свободного пробега молекул увеличивается и может стать больше размеров сосуда, в котором создается разрежение. При вакууме свыше 1 • 10 ~^мм ртутного столба длина свободного пробега молекул достигает нескольких метров.
При наиболее высоком достигнутом ныне вакууме
1 – 10 “11 мм ртутного столба длина свободного пробега молекул для воздуха (азота и кислорода) приближается к 5000 км. Состояние газа, когда длина свободного пробега молекул превышает размеры сосуда, в котором заключен газ, называется высоким вакуумом. Для обычной аппаратуры и приборов такое состояние достигается при давлении газа ниже 1 • 10 мм ртутного столба, когда длина свободного пробега молекул различных газов измеряется десятками сантиметров. Для наглядности представления о насыщении объема молекулами при различном вакууме приведем следующее сравнение. Увеличим размер одной молекулы до размера песчинки. Тогда одна песчинка при обычном состоянии газа будет приходиться на 40 кубических сантиметров пространства; это значит, что в объеме одного стакана будет находиться всего лишь 5 песчинок. А в высоком вакууме (при остаточном давлении 10~8 мм ртутного столба) одна песчинка будет приходиться в том же масштабе уже на три миллиона кубических метров пространства. В первом случае свободный пробег молекулы будет равен 60 см, а во втором 200 км.
Понятно, что свойства пространства, заполненного молекулами с такой различной плотностью, резко различаются.
Газ, находящийся в состоянии высокого вакуума, обладает необычными свойствами. Его физические свойства зависят от размеров сосуда, в котором он находится.
В состоянии высокого вакуума изменяется прежде всего характер передачи тепла и электричества в газе.
В чем же особенности этого удивительного состояния газа? При высоком вакууме в сообщающихся сосудах, имеющих разную температуру, давление будет не одинаковое. Чтобы доказать это, возьмем два сосуда с воздухом и соединим их трубкой. При обычных условиях давление в них будет одинаковым. Нагреем один из них; движение молекул в нем усилится и давление повысится; через некоторое время
то же произойдет и во втором сосуде. В результате давление в обоих сосудах снова будет одинаковым. А вот в таких же сосудах, где создан «высокий вакуум, при различной температуре давление будет разное. Это объясняется тем, что свойства газа в состоянии высокого вакуума в большой степени определяются состоянием стенок сосуда, в котором газ находится. Молекулы газа, ударяясь о стенки более горячего сосуда, приобретают большую энергию, чем в холодном, и, следовательно, их удары о стенки будут более сильными
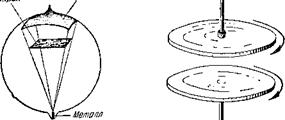
Рис. 9. В высоком вакууме молекулы движутся прямолинейно. |
Рис. 10. Вращение нижнего диска передается верхнему. |
И давление большим. Это давление не будет передаваться в соседний более холодный сосуд, так как число столкновений между молекулами мало и увеличение энергии молекул в другом сосуде будет незначительно.
Если в высоком вакууме между двумя стенками, имеющими различную температуру, поместить пластинку, то пластинка будет испытывать избыточное давление со стороны более нагретой стенки. Молекулы газа, ударившись о поверхность с более высокой температурой, приобретают большую скорость и с большей силой ударяют в пластинку. На этом принципе может быть основано измерение величины вакуума.
Прямолинейность движения молекул в высоком вакууме может быть показана на следующем опыте (рис. 9). Укрепим в стеклянном сосуде металлическую или слюдяную пластинку (экран). В углублении нижней части сосуда поместим небольшое количество легкоплавкого металла, например висмута. Откачаем воздух и запаяем сосуд. После этого нагреем металл. Молекулы металла, испаряясь, летят пря
молинейно и покрывают стенки сосуда тонким слоем. Лишь за пластинкой (экраном) остается «тень», то есть поверхность, не покрытая металлом.
При обычном давлении газы обладают определенной вязкостью, то есть если придать молекулам газа в какой-то части сосуда движение, то оно будет передаваться другим молекулам. Это видно на простом опыте. На рис. 10 показано два диска, способных свободно вращаться вокруг своей оси. Если привести во вращение нижний диск, то его движение передастся прилегающему к диску слою молекул газа и дальше распространится по объему газа и приведет во вращение верхний диск. Происходит это в результате взаимодействия движущихся молекул. В высоком вакууме вращение диска передаваться не будет, так как молекулы движутся, не «задевая» одна другую.
При высоком вакууме изменяется и прохождение электрического тока в газах. Подробнее об электрических явлениях в вакууме мы расскажем ниже.
М Ы познакомились с многочисленными свойствами «пустого» пространства и убедились, что оно далеко не пустое. Однако свойства многих веществ, направление ряда важных технических процессов в большой степени изменяются в разреженном …
И Спользование вакуума в повседневной жизни распространено так широко, что мы этого подчас и не замечаем. Зайдем на колхозную молочную ферму — идет доение коров. К вымени каждой из них …
В Елико давление воздуха на все, находящееся на дне воздушного океана. На каждый квадратный сантиметр поверхности любого тела давит сила, равная примерно 1 кг. С тех пор как была определена …
Источник
