Сосуд мариотта бойля мариотта

Воздух (или инертный газ), находящийся в запечатанном пакете с печеньем, расширяется, когда продукт поднят на значительную высоту над уровнем моря (ок. 2000 м)

Зако́н Бо́йля – Марио́тта – один из основных газовых законов, экспериментально установленный в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в 1676 году[1]. Описывает поведение газа в изотермическом процессе. С точки зрения современной физики закон представляет собой следствие уравнения Клапейрона – Менделеева[2].

Формулировки[править | править код]

Утверждение закона Бойля – Мариотта состоит в следующем[3][4][5]:

При постоянных температуре и массе газа произведение давления газа на его объём постоянно.

В математической форме это утверждение записывается в виде формулы

где – давление газа; – объём газа, а – постоянная в оговоренных условиях величина. В общем случае значение определяется химической природой, массой и температурой газа.

Очевидно, что если индексом 1 обозначить величины, относящиеся к начальному состоянию газа, а индексом 2 – к конечному, то приведённую формулу можно записать в виде

Из сказанного и приведённых формул следует вид зависимости давления газа от его объёма в изотермическом процессе:

Эта зависимость представляет собой другое, эквивалентное первому, выражение содержания закона Бойля – Мариотта[4][5] . Она означает, что

Давление некоторой массы газа, находящегося при постоянной температуре, обратно пропорционально его объёму.

Тогда связь начального и конечного состояний газа, участвовавшего в изотермическом процессе, можно выразить в виде:

Следует отметить, что применимость этой и приведённой выше формулы, связывающей начальные и конечные давления и объёмы газа друг с другом, не ограничивается случаем изотермических процессов. Формулы остаются справедливыми и в тех случаях, когда в ходе процесса температура изменяется, но в результате процесса конечная температура оказывается равной начальной.

Важно уточнить, что данный закон справедлив только в тех случаях, когда рассматриваемый газ можно считать идеальным. В частности, с высокой точностью закон Бойля – Мариотта выполняется применительно к разреженным газам. Если же газ сильно сжат, то наблюдаются существенные отступления от этого закона.

Закон Бойля – Мариотта, закон Шарля и закон Гей-Люссака, дополненные законом Авогадро, являются достаточной основой для получения уравнения состояния идеального газа.

Следствия[править | править код]

Закон Бойля – Мариотта утверждает, что давление газа в изотермическом процессе обратно пропорционально занимаемому газом объёму. Если учесть, что плотность газа[6] также обратно пропорциональна занимаемому им объёму, то мы придём к заключению:

При изотермическом процессе давление газа изменяется прямо пропорционально его плотности.

Известно, что сжимаемость, то есть способность газа изменять свой объём под действием давления, характеризуется коэффициентом сжимаемости[7]. В случае изотермического процесса говорят об изотермическом коэффициенте сжимаемости, который определяется формулой

где индекс T означает, что частная производная берётся при постоянной температуре. Подставляя в эту формулу выражение для связи давления и объёма из закона Бойля – Мариотта, получаем[5]:

Таким образом, приходим к выводу:

Изотермический коэффициент сжимаемости идеального газа равен обратной величине его давления.

См. также[править | править код]

Закон Гей-Люссака
Закон Шарля
Закон Авогадро
Идеальный газ
Уравнение состояния идеального газа

Примечания[править | править код]

Литература[править | править код]

Петрушевский Ф. Ф. Бойля-Мариотта закон // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). – СПб., 1890-1907.

Источник

В уроке 25 «Закон Бойля-Мариотта» из курса «Химия для чайников» рассмотрим закон, связывающий давление и объем газа, а также графики зависимости давления от объема и объема от давления. Напомню, что в прошлом уроке «Давление газа» мы рассмотрели устройство и принцип действия ртутного барометра, а также дали определение давлению и рассмотрели его единицы измерения.

Роберт Бойль (1627-1691), которому мы обязаны первым практически правильным определением химического элемента (узнаем в гл. 6), интересовался также явлениями, происходящими в сосудах с разреженным воздухом. Изобретая вакуумные насосы для выкачивания воздуха из закрытых сосудов, он обратил внимание на свойство, знакомое каждому, кому случалось накачивать камеру футбольного мяча или осторожно сжимать воздушный шарик: чем сильнее сжимают воздух в закрытом сосуде, тем сильнее он сопротивляется сжатию. Бойль называл это свойство «пружинистостью» воздуха и измерял его при помощи простого устройства, показанного на рис. 3.2, а и б.

Бойль запирал ртутью немного воздуха в закрытом конце изогнутой трубки (рис. 3-2, а) а затем сжимал этот воздух, понемногу добавляя ртуть в открытый конец трубки (рис. 3-2, б). Давление, испытываемое воздухом в закрытой части трубки, равно сумме атмосферного давления и давления столбика ртути высотой h (h – высота, на которую уровень ртути в открытом конце трубки превышает уровень ртути в закрытом конце). Полученные Бойлем данные измерения давления и объема приведены в табл. 3-1. Хотя Бойль не предпринимал специальных мер для поддержания постоянной температуры газа, по-видимому, в его опытах она менялась лишь незначительно. Тем не менее Бойль заметил, что тепло от пламени свечи вызывало значительные изменения свойств воздуха.

Анализ данных о давлении и объеме воздуха при его сжатии

Таблица 3-1, которая содержит экспериментальные данные Бойля о взаимосвязи давления и объема для атмосферного воздуха, расположена под спойлером.

После того как исследователь получает данные, подобные приведенным в табл. 3-1, он пытается найти математическое уравнение, связывающее между собой две зависящие друг от друга величины, которые он измерял. Один из способов получения такого уравнения заключается в графическом построении зависимости различных степеней одной величины от другой в надежде получить прямолинейный график. Общее уравнение прямой линии имеет вид:

y = ах + b (3-2)

где х и у – связанные между собой переменные, а a и b – постоянные числа. Если b равно нулю, прямая линия проходит через начало координат.

На рис. 3-3 показаны различные способы графического представления данных для давления Р и объема V, приведенных в табл. 3-1. Графики зависимости Р от 1/К и зависимости V от 1/Р представляют собой прямые линии, проходящие через начало координат. График зависимости логарифма Р от логарифма V также является прямой линией с отрицательным наклоном, тангенс угла которого равен – 1. Все эти три графика приводят к эквивалентным уравнениям:

P = a / V (3-3а)
V = a / P (3-3б)

lg V = lg а – lg Р (3-3в)

Каждое из этих уравнений представляет собой один из вариантов закона Бойля-Мариотта, который обычно формулируется так: для заданного числа молей газа его давление пропорционально объему, при условии что температура газа остается постоянной.

Кстати, наверняка вам стало интересно, почему закон Бойля-Мариотта назван двойным именем. Это произошло так, потому что этот закон независимо от Роберта Бойля, который открыл его в 1662 году, был переоткрыт Эдмом Мариоттом в 1676 году. Вот так вот.

Когда взаимосвязь между двумя измеряемыми величинами проста до такой степени, как в данном случае, ее можно установить и численным способом. Если каждое значение давления Р умножить на соответствующее значение объема V, нетрудно убедиться, что все произведения для заданного образца газа при постоянной температуре оказываются приблизительно одинаковыми (см. табл. 3-1). Таким образом, можно записать, что

P·V = а ≈ 1410 (3-3г)

Уравнение (З-Зг) описывает гиперболическую зависимость между величинами Р и V (см. рис. 3-3,а). Для проверки того, что построенный по экспериментальным данным график зависимости Р от V действительно соответствует гиперболе, построим еще дополнительный график зависимости произведения P·V от Р и убедимся, что он представляет собой горизонтальную прямую линию (см. рис. 3-3,д).

Бойль установил, что для заданного количества любого газа при постоянной температуре взаимосвязь между давлением Р и объемом V вполне удовлетворительно описывается соотношением

P·V = const (при постоянных Т и n) (3-4)

Формула из закона Бойля-Мариотта

Для сопоставления объемов и давлений одного и того же образца газа при различных условиях (но постоянной температуре) удобно представить закон Бойля-Мариотта в следующей формуле:

P1·V1 = Р2·V2 (3-5)

где индексы 1 и 2 соответствуют двум различным условиям.

Пример 4. Доставляемые на плато Колорадо пластмассовые мешочки с пищевыми продуктами (см. пример 3) часто лопаются, потому что воздух, находящийся в них, при подъеме от уровня моря на высоту 2500 м, в условиях пониженного атмосферного давления, расширяется. Если предположить, что внутри мешочка при атмосферном давлении, соответствующем уровню моря, заключено 100 см3 воздуха, какой объем должен занимать этот воздух при той же температуре на плато Колорадо? (Допустим, что для доставки продуктов используются сморщенные мешочки, не ограничивающие расширение воздуха; недостающие данные следует взять из примера 3.)

Решение

Воспользуемся законом Бойля в форме уравнения (3-5), где индекс 1 будем относить к условиям на уровне моря, а индекс 2 – к условиям на высоте 2500 м над уровнем моря. Тогда Р1 = 1,000 атм, V1 = 100 см3, Р2 = 0,750 атм, а V2 следует вычислить. Итак,

P1·V1 = Р2·V2
1,000 атм · 100 см3 = 0,750 атм · V2

откуда

V2 = 133 см3

Надеюсь, что после изучения урока 25 «Закон Бойля-Мариотта» вы запомните зависимость объема и давления газа друг от друга.. Если у вас возникли вопросы, пишите их в комментарии. Если вопросов нет, то переходите к следующему уроку.

Хотите ещё проще? Мы создали новый курс, где максимум за 7 дней вы овладете химией с нуля. Подробннее по ссылке

Источник

★ Сосуд Мариотта

Сосуд Мариота – это устройство, которое обеспечивает равномерное истечение струи жидкости за счет постоянного давления. он был изобретен французским физиком XVII Admom века Марриотт.

1. Принцип работы. (The principle of operation)

Сифон отель Marriott представляет собой герметически закрытый сосуд, в который вставлен крышку открытой с обоих концов трубки один конец погружен в жидкость, а другая, сообщающаяся с атмосферой.

Изначально, когда все клапаны и сообщающимся с атмосферой отверстия в трубе закрыты, уровень жидкости в трубке совпадает с уровнем жидкости в сосуде. если вы заполняете сосуд с жидкостью не полностью над ее поверхностью будет иметь определенное количество воздуха и давление P {свойства стиль отображения значение Р,} в нижней части трубы рассчитывается по формуле:

P = ρ g h 0 (г ч 0) + p 0 {displaystyle P=rho gh_{0}+p_{0}}, где:

Ρ {свойства стиль отображения значение РО } – плотность жидкости.
G {свойства стиль отображения значение g} (g {the style property display the value of g}) – ускорение свободного падения.
P 0 {свойства стиль отображения значение p_{0}} (p 0 {the style property display the value of p_{0}}) – давление в пространстве над водой атмосферном давлении.
H 0 {свойства стиль отображения значение h_{0}} (h 0 {the style property display the value of h_{0}}) – расстояние между поверхностью жидкости и нижней части трубы.

Если открыть клапан 3, а затем в трубу, вытесняя жидкость в нем будет наполняют воздух, и давление над поверхностью будет равна p 0 − ρ g h 0 (г ч 0) {свойства стиль отображения значение Р{0}-РО gh_{0}}. в конце трубы устанавливают в атмосферном давлении p 0 {свойства стиль отображения значение p_{0}}. жидкости из отверстия начнут появляться только под давлением столба жидкости между клапанами 2 и 3 на Рис., которая остается постоянной все время, пока конец трубки остается погруженным в жидкость. Через патрубок в верхней части сосуда будет поступать воздух.

Скорость движения жидкости может быть определена по формуле Торричелли:

v = 2 g h (в = 2 г) {displaystyle v={sqrt {2gh}}}, где h {displaystyle h} – расстояние между нижним концом трубки и клапаном или между клапанами 2 и 3 на рис.

Если когда клапан открыт 3, чтобы открыть клапан 2, расположенном на нижнем конце трубки, жидкость из него вытекать не будет из-за равенства давления с обеих сторон клапана. если клапан открыт 3, чтобы открыть клапан 1, жидкости не вытекают, а не через клапан 1 в судно войдет воздух, и давление на клапан 3 и скорость струи потока от него будет увеличиваться.

2. Приложение. (App)

Основное свойство судна Marriott-это то, что он позволяет регулировать скорость потока жидкости. он используется в системах непрерывной подачи чернил СНПЧ, дозирования жидкостей в лабораторных условиях, в топливные баки для горелки испарительного типа в малых котлов.

картриджи СНПЧ. Посредством этого, а также устройства доноров в виде сосудов Мариотта достигается необходимое постоянное наличие чернил в печатающей головке
1787 года данных Шарля Закон Гей – Люссака, закон Шарля и закон Бойля – Мариотта все вместе образуют объединённый газовый закон. В сочетании с законом Авогадро
изолированного сердца и одновременной его электростимуляции. Сфигмограф Маре Сосуд Мариотта – используется для подачи перфузионного раствора при исследованиях
взрывной декомпрессии, а также в некоторых других случаях. Закон Бойля – Мариотта определяет отношение между объёмом воздушного пространства и окружающего
содержалась ошибка, так как он предполагал скорость вытекания жидкости из сосуда пропорциональной расстоянию отверстия до поверхности воды. Торричелли заметил
закона, названного впоследствии законом Бойля – Мариотта в связи с тем, что французский физик Эдм Мариотт в 1679 г. провёл аналогичное независимое исследование
проанализировав причины отклонения свойств реальных газов от закона Бойля – Мариотта вывел уравнение состояния реального газа, в котором были учтены собственный
молекулярной физикой, в частности, изучал отклонения от закона Бойля – Мариотта Эрстед обладал не только научным, но и педагогическим талантом, вёл просветительскую
что и Дальтон. Впоследствии он же объединил свой закон с законом Бойля – Мариотта что позволило описывать в том числе и изохорный процесс. Из определения
растворенного вещества, моль м3. Это уравнение по форме совпадает с законом Бойля – Мариотта для идеальных газов. Поэтому осмотическое давление разведенных растворов
объёме давление с уменьшением объёма увеличивается согласно закону Бойля – Мариотта В конце концов, начиная с какого – то значения, давление не будет изменяться
времени нужно считать одним из самых трудных, и установление закона Бойля – Мариотта около 1676 года – одним из самых важных завоеваний человеческого ума того

он поместил её в стеклянный сосуд особого устройства, который был после того герметически закупорен и взвешен. Вес сосуда без воды был определён ранее
1662 году данные опыты позволили прийти к формулировке закона Бойля – Мариотта В 1779 году в Пирометрии Ламберта был описан опыт повышения и понижения
объёмом и абсолютной температурой идеального газа, обобщает законы Бойля – Мариотта Шарля и Гей – Люссака. В том же году вместе с Л. Тенаром разработал способ
дочь Азазеля использует девушку по имени Мэг Мастерс Никки Эйкокс как сосуд В премьерной серии второго сезона тело, которое занял Азазель, сыграл Фредрик
демонстрирует зависимость между объёмом и упругостью воздуха см. закон Бойля – Мариотта одновременно он указывает на то, что эта закономерность не распространяется
демонстрирует зависимость между объёмом и упругостью воздуха см. закон Бойля – Мариотта тут же указывает на дискретность её для воздуха при сильном его сжатии
механики закон всемирного тяготения и газовой динамики закон Бойля – Мариотта Статью рассматривал профессор Иван Боргман. По мнению Циолковского, она
открытий, включая связь между объёмом и давлением газа закон Бойля – Мариотта В других трудах Бойль утверждает, что материя состоит из мелких частиц

Источник

, ; , , .
, : “, “; , .
. 1:9-10

, . . , . .

– , , , .

, XX . «» 1974 ,

” , , 1 () 10^−9 . «» .”

, 1959 :

, “.

, « » .

, , , 1857 , .

, , . , , … . 5 .

/, V-IV (: ). .

: V .. I .. ( 1940- .)

: 20 .

: .

. , «» – . , . – . , III , , , , .

. , , 1838-1839 . , , .

, , . V . .. III .., .

1940- .

( ἄσβεστος, ) hrysotile (Mg3Si2O5(OH)4) . JEOL.

3 1 (, ) . ( ) , , (~ 600-700°C) . , , ( , ) . , , .

, . , , .

The fascinating world of nanoparticle re, Materials Today, 2013.

The ideal ceramic-fibre/oxide-matrix composite: How to reconcile antagonist physical and chemical requirements? Annales de Chimie Science des Matériaux, 2005.

The Use of l Nanoparticles to Produce Yellow, Red and Iridescent Colour, from Bronze Age to Present s in Lustre Pottery and Glass: Solid e Chemistry, Spectroscopy and Nanostructure. Journal of Nano Re, 2009.

Techological approach of ceramic production at the end of the iron age at I Palazzi (North-Eastern Corsica). The Old Potters Almanack, 2015.

( ), 2000 . .

: I

: PbS 5 .

: .

4000 . , . , , , , , . , 614 . , . , , , – . , , .

, , – . L’Oreal . , . , ” ” , (PbS), , . , I .

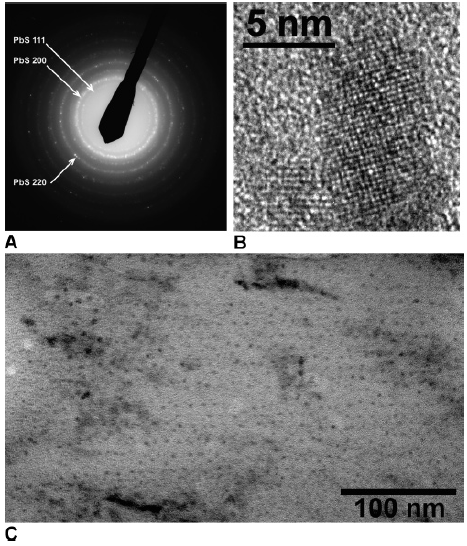
(HRTEM) PbS . (A) : d PbS. (B) PbS. (C) 3 . .

: PbO Ca(OH)2 . . , – (PbS) . , , , , . PbS 5 , 200 .

TEM ( ) , PbS . 8-10 , «» . , , .

, .

Hair in Egypt, Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, 2008.

Early Use of PbS Nanotechnology for an Ancient Hair Dyeing Formula, Nano Lett., 2006.

Ancient Hair-Dyeing A Nanoscience? Phys.org.

() () . .

: IV ..

: , .

: 50-100 .

: .

, IV . . : , .

, . , , , . -, . . , , , .

. XIX , . 1958 20 000 .

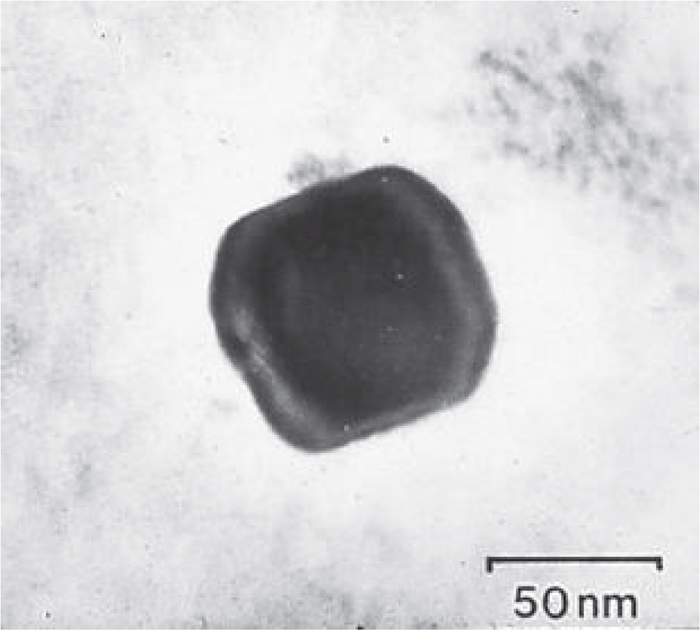
, — , ( ). 0,5% , 0,3% 0,04% . (0,3% ), .

, . 70 . , .

. , , , , «» .

Nanotechnology: from the ancient to nowadays, Foundations of Chemistry, 2015.

-, , 2017.

The Lycurgus Cup A Roman nanotechnology, Gold Bulletin, 2007.

The Rothschild Lycurgus Cup, The Antiquaries Journal, 1959 .

, , , XIII .

: IX-XVI

: , .

: 5-10

: .

, – . ( , ), .

, , (/ ?) VI VII . IX . , ( X ), (XXIV ). , XIV XVI , Paterna Manises, , XV XVI , Deruta Gubbio.

, X , XII . (1301 ). – -, .

Cipriano Piccolpasso «Li tre libri dell’arte del vasajo» ( , 1557 ). , .

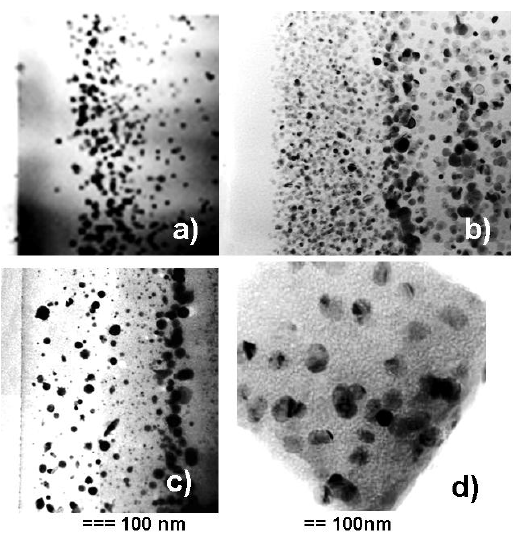
TEM ( ) : ) ( , IX , Ph. Sciau), b) c ( ) ) Eva Hundum, d) , . .

, / , (, ), , . 600◦C , . .

, – . , . .

(TEM) (510 ) (520 ) . 430 , . , , , , , , -.

. .

XAFS study of copper and silver nanoparticles in glazes of medieval middle-east lustreware (10th13th century), Applied Physics A, 2006.

5. Assadullah Isfahani

( ), XVII . , , , ( ). Mohammeds ladder wootz , «kirk narduban». : عمل اسد الله اصفهانی « ». : بنده شاه ولایت عباس « Trusteeship Abbas». Runjeet Singh.

: 1600-1628 .

: , .

: 40-50 .

: .

, , . , , , . , , , . . .

2004 XVII (HR TEM). , (Fe3C) . .

. XVII (1587- 1628) . , «wootz». , wootz, , XVIII . , .

0,349 , , . .

, . , , , , . , , , , . , . , . , , , , .

Nanowires in ancient Damascus steel, Journal of Alloys and Compounds, 2004.

Microstructure of a Damascene sabre after annealing, International Journal of Materials Re, 2006

Structure of several historic blades at nanoscale, Crystal Re and Technology, 2009

Discovery of Nanotubes in Ancient Damascus Steel, Physics and Engineering of New Materials, 2009

Carbon nanotechnology in an 17th century Damascus sword, National Geographic, 2008.

Assad Ullah ( , XVII .)

Sabre or shamshir by Assad Ullah.

, XVII , .

6. Cacaxtla

Mural del Templo Rojo, Cacaxtla, 3D .

: 650-900 ..

: , .

: . 50 ;

4.0+-0.6 .

: ;

? !

. . , .

, . , (, , .) ( , , .) , , , . , , , , , , .

, !

, , , .

Источник