Сосуд объема разделен на две равные

Молекулы разных газов отличаются по размеру. Поэтому один газ можно запереть в некотором объеме, а другой проникнет через ячею и займет пространство за перегородкой. А значит, его давление изменится, потому что теперь он занимает больший объем. В то же время давление в сосуде, где находятся два газа, является суммой их парциальных (частных) давлений. На этих соображениях и построим решение следующих задач.
Задача 1. Для приготовления газовой смеси с общим давлением 0,5 кПа к сосуду с объемом 10 дм присоединили баллон объемом 1 дм, в котором находится гелий под давлением 4 кПа, и баллон с неоном под давлением 1 кПа. Найдите объем баллона с неоном. Температура постоянна.
Каждый из газов создает парциальное давление. И, так как температура постоянна, мы можем воспользоваться законом Бойля-Мариотта для определения этих парциальных давлений. Сначала гелий находится в сосуде объемом , а потом клапаны открывают и он занимает весь предоставленный объем:
Пусть – объем сосуда с неоном, а дм – объем, в котором готовят смесь.
Тогда для неона запишем аналогично:
Найдем парциальные давления газов:
Тогда давление в баллоне для смеси – это сумма парциальных давлений:
Откуда определяем :
Ответ: 3 дм.

К задачам 2 и 3
Задача 2. Одинаковые по массе количества водорода и гелия находятся в сосуде объемом , который отделен от пустого сосуда объемом полупроницаемой перегородкой, свободно пропускающей молекулы водорода и не пропускающей гелий. После установления равновесия давление в первом сосуде упало в 2 раза. Определите отношение . Температура постоянна. Молярная масса водорода 2 г/моль, гелия 4 г/моль.
Так как молекулы водорода могут проникать через перегородку, то ее как бы и нет для водорода. То есть его давление будет совершенно одинаковым в обеих частях сосуда, и в первой, и во второй. Но во второй части нет атомов гелия, поэтому давление в ней определяется только наличием водорода и равно давлению водорода. В первой же части гелий есть, и в этой части давление будет складываться из парциальных давлений гелия и водорода. Тогда согласно уравнению Менделеева-Клапейрона давления (парциальные) газов изначально равны:
Суммарное давление:
После того, как молекулы водорода проникнут через перегородку, его давление станет равно:
Теперь суммарное давление в первой части сосуда
И оно в два раза меньше прежнего:
Тогда:
Сократим все, что можно:
Так как массы газов равны, то еще упрощаем:
Домножим на :
Теперь упростим правую часть:
Разделим на :
Ответ: .
Задача 3. Сосуд объемом 2 дм разделен на две равные части полупроницаемой перегородкой. В первую половину сосуда введена смесь аргона массой 20 г и водорода массой 2 г, во второй половине – вакуум. Через перегородку может диффундировать только водород. Какое давление установится в первой половине сосуда после окончания процесса диффузии? Во время процесса поддерживалась температура С. Перегородка неподвижна.
Суммарное давление газов в первой половине в начале процесса:
Где
Затем водород проникнет через перегородку, и его давление упадет, станет равным:
Тогда давление в той половине, где есть аргон, станет равно:
Ответ: Па.
Источник
1. Так как сосуд теплоизолирован и начальные температуры газов одинаковы, то после установления равновесия температура в сосуде будет равна первоначальной, а гелий равномерно распределится по всему сосуду. После установления равновесия в системе в каждой части сосуда окажется по моль гелия: В результате в сосуде с аргоном окажется моль смеси:
2. Внутренняя энергия одноатомного идеального газа пропорциональна температуре и количеству молей:
3. Запишем условие термодинамического равновесия:
4.
Ответ:
Порядок назначения третьего эксперта
В соответствии с Порядком проведения государственной итоговой
аттестации по образовательным программам среднего общего образования
(приказ Минобрнауки России от
зарегистрирован
Минюстом России
)
« По результатам первой
и второй проверок эксперты независимо
друг от друга выставляют баллы за каждый ответ на задания
экзаменационной работы ЕГЭ с развёрнутым ответом…
В случае существенного расхождения в баллах, выставленных
двумя экспертами, назначается третья проверка. Существенное расхождение
в баллах определено в критериях оценивания по соответствующему
учебному предмету.
Эксперту, осуществляющему третью проверку, предоставляется
информация о баллах, выставленных экспертами, ранее проверявшими
экзаменационную работу».
Если расхождение составляет
и более балла за выполнение задания, то третий эксперт проверяет ответы только на то задание, которое
вызвало столь существенное расхождение.
Критерии оценки
3 баллаПриведено полное решение, включающее следующие элементы:
I. записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: формула для внутренней энергии одноатомного идеального газа, условие
термодинамического равновесия);
II. описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов);
III. проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
IV. представлен правильный ответ
2 баллаПравильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в
записи единиц измерения величины)
1 баллПредставлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения данной задачи (или утверждение, лежащее в основе
решения), но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения
данной задачи (или в утверждении, лежащем в основе решения),
допущена ошибка, но присутствуют логически верные
преобразования с имеющимися формулами, направленные на
решение задачи
0 балловВсе случаи решения, которые не соответствуют вышеуказанным
критериям выставления оценок в балла
Источник
11. МКТ и Термодинамика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
На рисунке показана зависимость давления газа (p) от его плотности (rho) в циклическом процессе, совершаемом 2 моль идеального газа в идеальном тепловом двигателе. Цикл состоит из двух отрезков прямых и четверти окружности.
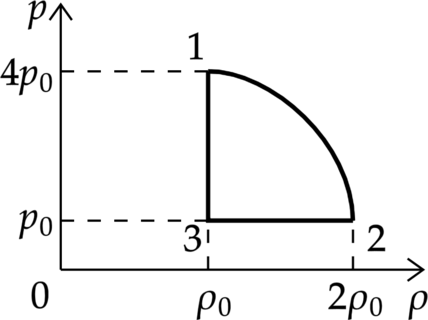
На основании анализа этого циклического процесса выберите два верных утверждения.
1) В процессе 1−2 температура газа уменьшается.
2) В состоянии 3 температура газа максимальна.
3) В процессе 2−3 объём газа уменьшается.
4) Отношение максимальной температуры к минимальной температуре в цикле равно 8.
5) Работа газа в процессе 3−1 положительна.
“Демоверсия 2017”
1) По уравнению Клапейрона – Менделеева: [p=dfrac{rho}{mu}RT,] где (T) – температура, (mu) – молярная масса газа.
Давление уменьшилось в 4 раза, а плотность увеличилась в 2 раза, следовательно, температура уменьшилась в 8 раз.
Утверждение 1 – (color{green}{small text{Верно}})
2) Аналогично предыдущему пункту [p=dfrac{rho}{mu}RT] Максимальная температура будет в состоянии 1 (давление максимально, плотность минимальна)
Утверждение 2 – (color{red}{small text{Неверно}})
3) В процессе 2 – 3 плотность меньшается, а по формуле: [rho =dfrac{m}{V}] Объем увеличивается
Утверждение 3 – (color{red}{small text{Неверно}})
4) Аналогично пункту 2, минимальность температуры будет достигнута в точке с наименьшим давлением и наибольшей плотностью (т. 2), а отношение температур действительно равно 8
Утверждение 4 – (color{green}{small text{Верно}})
5) В процессе 2 – 3 плотность постоянна, следовательно, объем постоянен и газ не совершает работу.
Утверждение 5 – (color{red}{small text{Неверно}})
Ответ: 14
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В начальный момент времени в левой части сосуда содержится 4 моль гелия, в правой – 40 г аргона. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул аргона. Температура газов одинаковая и остаётся постоянной. Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Концентрация гелия в правой части сосуда в 2 раза меньше, чем аргона.
2) Отношение давления газов в правой части сосуда к давлению газа в левой части равно 1,5.
3) В правой части сосуда общее число молекул газов меньше, чем в левой части.
4) Внутренняя энергия гелия и аргона одинакова.
5) В результате установления равновесия давление в правой части сосуда увеличилось в 3 раза.
“Демоверсия 2020”
Перегородка проницаема только для молекул гелия, поэтому в результате установления равновесия парциальное давление гелия в левой части будет равно парциальному давлению гелия в правой части. Давление газа можно вычислить по формуле: [p=dfrac{nu R T}{V}] Парциальные давления гелия в левой и правой части одинаковы, одинаковы температуры и объёмы частей, следовательно, одинаковы и количества вещества гелия в левой и правой частях сосуда, то есть в левой и правой части сосуда будет содержаться по 2 моля гелия.
Найдём связь концентрации и количества вещества: [n=dfrac{N}{V}=dfrac{nu N_A}{V}] То есть концентрации и количества вещества зависят прямо пропорционально друг от друга, также заметим, что чем больше количество вещества, тем больше и количество молекул.
Найдём количество вещества аргона: [nu_{Ar}=dfrac{m_{Ar}}{mu_{Ar}}=dfrac{40text{ г}}{40text{ г/моль}}=1text{ моль}]
Используя полученное выше, рассмотрим данные в задании утверждения.
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
1) (color{red}{small text{Неверно}})
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
2) (color{green}{small text{Верно}})
Отношение давлений: [dfrac{p_text{ п}}{p_text{ л}}=dfrac{nu_text{ г.п}+nu_{Ar}}{nu_text{ г.л}}=dfrac{2text{ моль}+1text{ моль}}{2text{ моль}}=1,5] Где (nu_{text{ г.п.}},nu_{text{ г.л.}}) – количество вещества гелия в правой части, количество вещества гелия в левой части соответственно.
3) (color{red}{small text{Неверно}})
Количество вещества газов в правой части сосуда больше количества вещества газа в левой части сосуда, следовательно, в правой части сосуда общее число молекул газа больше, чем в левой части сосуда.
4) (color{red}{small text{Неверно}})
Внутренняя энергия одноатомного идеального газа может быть вычислена по формуле: [U=dfrac{3}{2}nu R T] Температура газов одинакова. Количество вещества гелия больше количества вещества аргона, следовательно, внутренняя энергия гелия больше внутренней энергии аргона.
5) (color{green}{small text{Верно}})
айдём отношение конечного давления в правой части сосуда к начальному давлению в правой части сосуда: [dfrac{p_{k}}{p_text{ н}}=dfrac{nu_{text{ г.п.}}+nu_{Ar}}{nu_{Ar}}=dfrac{2text{ моль}+1text{ моль}}{1text{ моль}}=3]
Ответ: 25
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ нагревают.
Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Объём газа в этом процессе остаётся неизменным.
2) Давление газа в сосуде остаётся неизменным.
3) Плотность газа в этом процессе увеличивается.
4) Сила Архимеда, действующая на шарик, уменьшается.
5) Концентрация молекул газа в сосуде увеличивается.
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлениии.
Уравнение состояния газа: [pV=nu RT] где (nu) — количество вещества, (T) — температура в Кельвинах, (p) — давление газа, (V) — объем, занимаемый газом, (R) — универсальная газовая постоянная. Выразим объем [V=dfrac{nu RT}{p}] При нагревании газа объем увеличивается.
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Утверждение 2 — (color{green}{smalltext{Верно }})
3) Плотность газа: [rho=dfrac{m}{V}] При нагревании объем увеличивается, значит плотность уменьшается.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Сила Архимеда: [F_{text{Арх}}=rho gV] где (rho) — плотность газа, (V) — объем шарика, (g) — ускорение свободного падения. Плотность уменьшается, значит, сила Архимеда уменьшается.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Концентрация: [n=dfrac{N}{V}] При нагревании газа объем увеличивается, концентрация уменьшается.
Утверждение 5 — (color{red}{smalltext{Неверно }})
Ответ: 24
На (pV)—диаграмме отображена последовательность трёх процессов (1 — 2 — 3) изменения состояния 2 моль идеального газа. 
Из предложенного перечня утверждений выберите два правильных и укажите их номера.
1) В процессе 1 газ отдаёт положительное количество теплоты.
2) Процесс 2 является изотермическим.
3) В процессе 3 газ совершает работу.
4) В процессе 2 происходит расширение газа при постоянной температуре.
5) В процессе 1 происходит сжатие газа при постоянной температуре.
Работа газа находится как площадь под графиком 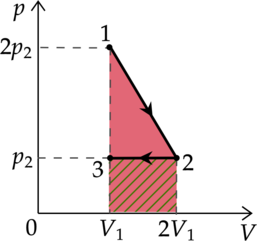
1) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. (Delta U=0), так как температура в процессе 1 не изменяется. При увеличении давления в изотермическом процессе объём уменьшается. (Delta V<0), следоватлеьно, (A<0). Таким образом, (Q<0), то есть газ отдает кол-во теплоты в данном процессе.
Утверждение 1 — (color{green}{smalltext{Верно }})
2) В процессе 2 температура увеличивается.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) (p=const), следовательно (Vsim T)
Температура уменьшается, то есть объем тоже уменьшается, (Delta V<0), (A<0)
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В процессе 2 температура увеличивается.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Температура в процессе 1 не изменяется. По закону Бойля-Мариотта (p V=const) так как давление увеличивается объём уменьшается.
Утверждение 5 —(color{green}{smalltext{Верно }})
Ответ: 15
На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах (V-T), где (V) — объём газа, (T) — абсолютная температура газа. Количество вещества газа постоянно. 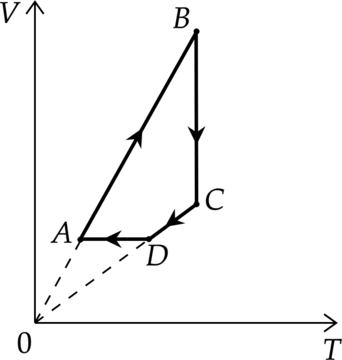
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.
1) В состоянии (B) концентрация газа максимальна.
2) В процессе (AB) газ отдаёт некоторое количество теплоты.
3) В процессе (BC) внутренняя энергия газа увеличивается.
4) Давление газа в процессе (CD) постоянно, при этом внешние силы совершают над газом положительную работу.
5) В процессе (DA) давление газа изохорно уменьшается.
1) В точке (B) объем максимален, а концентрация минимальна:
Утверждение 1 —(color{red}{smalltext{Неверно }})
2) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. В процессе (AB) работа равна (0), температура увеличивается, то есть (Delta U>0), значит (Q>0), то есть газ получает тепло
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс (BC) — изотермический. Внутренняя энергия не меняется.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Процесс (СD) — изобарное сжатие. При уменьшении объема внешние силы совершают положительную работу.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Процесс (DA) — изохорное охлаждение ((psim T)). Следовательно, при уменьшении температуры давление уменьшается.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Идеальный газ перевели из состояния 1 в состояние 3 так, как показано на графике зависимости давления р газа от объёма V. Количество вещества газа при этом не менялось. 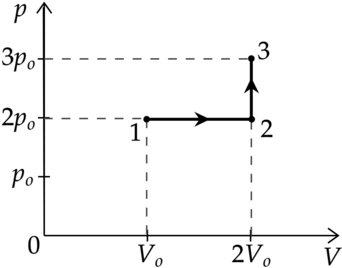
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике.
1)Абсолютная температура газа минимальна в состоянии 2.
2)В процессе 1-2 абсолютная температура газа уменьшилась в 2 раза.
3)В процессе 2-3 абсолютная температура газа уменьшилась в 1,5 раза.
4)Плотность газа максимальна в состоянии 1.
5)В ходе процесса 1-2-3 средняя квадратичная скорость теплового движения молекул газа увеличилась в (sqrt{3}) раза.
1) Уравнение состояния газа: [pV=nu RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещеста, (R) — универасальная газовая постоянная, (T) — температура. Температура максимальна там, где максимально произведение (pV), поэтому из графика видно, что (T_1 – min), (T_3 – max), (T_1<T_2<T_3)
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Процесс 1-2 — изобарное расширение ((Vsim T)). Объем увеличился в 2 раза, то есть температура тоже увеличилась в 2 раза.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс 2-3 — изохорное нагревание. (V=const), следовательно (psim T) Давление увеличивается в 1,5 раза, то есть температура тоже увеличивается в 1,5 раза.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В точке 1 — объем минимален, следовательно, плотность там максимальна.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) [E_{k}=dfrac{3}{2}kT] [dfrac{m_0 v^2}{2}=dfrac{3}{2}kT] где (m_0) — масса газа, (v^2) средняя квадратичная скорость [v^2sim T] [vsim sqrt{T}] Температура в процессе 1-2-3 увеличилась в 3 раза, значит средняя квадратичная скорость увеличилась в (sqrt{3}) раз
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В левой части сосуда содержится 40 г неона, в правой — 2 моль гелия. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул неона. Температура газов одинакова и остаётся постоянной.
Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Внутренняя энергия гелия в сосуде меньше, чем внутренняя энергия неона.
2) Концентрация гелия в левой части сосуда в 2 раза больше концентрации неона.
3) В левой части сосуда общее число молекул газов в 3 раза больше, чем в правой части.
4) Внутренняя энергия гелия в сосуде в конечном состоянии меньше, чем в начальном.
5) В конечном состоянии давление в левой части сосуда в 3 раза больше, чем в правой.
1) Молярная масса неона (M=20) г/моль. Количество неона: [nu=dfrac{m}{M}=dfrac{40text{ г}}{20text{ г/моль}}=2 text{ моль}] Гелий займет все пространство сосуда, значит в левой части будет 3 моля вещества (1 моль гелия и 2 моль неона).
В правой части будет тоже 1 моль гелия.
Внутренняя энергия газа: [U=dfrac{i}{2}nu RT] Газы находятся при одинаковой температуре, количество гелия равно количеству неона. Внутренняя энергия гелия равна внутренней энергии неона
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) В левой части сосуда количество гелия в два раза меньше количества неона. Следовательно, концентрация гелия в два раза меньше концентрации неона.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Так как количество вещества в левой части сосуда больше в 3 раза, чем в правой, то и количество молекул также больше в 3 раза.
Утверждение 3 — (color{green}{smalltext{Верно }})
4) Так как температура гелия и общее количество гелия в сосуде не изменилось, то и внутреннняяя энергия не поменялась.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Давление газа: [p=nkT] Так как кол-во вещества в левой части сосуда больше в 3 раза, чем в правой, температуры одинаковые, то давление в конечном состоянии больше в левой части в 3 раза, чем в правой.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 35
Источник
