Сосуд объемом 20 л содержит воздух
В данной работе предлагается определенный подход к классификации и способам решения задач на газовые законы. Такой подход позволит быстро сориентироваться в большом количестве задач на свойства газов и применить к ним те или иные приемы решения.
Основные теоретические сведения
Состояние газа характеризуется совокупностью трех физических величин или термодинамических параметров:объемом газа V, давлением Р и температурой Т. Состояние газа, при котором эти параметры остаются постоянными считают равновесным состоянием.В этом состоянии параметры газа связаны между собой уравнением состояния. Самый простой вид уравнение состояния имеет для идеального газа. Идеальным газом называют газ, молекулы которого не имеют размеров (материальные точки) и взаимодействуют друг с другом лишь при абсолютно упругих соударениях (отсутствует межмолекулярное притяжение и отталкивание). Реальные газы тем точнее подчиняются законам идеальных газов, чем меньше размеры их молекул (т.е. газ одноатомный), и чем больше он разряжен.
Уравнение состояния идеального газа или уравнение Менделеева-Клапейрона имеет вид:
– универсальная газовая постоянная
Из этого закона вытекает, что для двух произвольных состояний газа справедливо равенство, называемое уравнением Клапейрона:
Так же для идеальных газов имеют место следующие экспериментальные законы:
Закон Бойля — Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, то результирующее давление определяется по закону Дальтона: давление смеси равно сумме давлений, производимых каждым газом в отдельности, как если бы он один занимал весь сосуд.
Р = Р1 + Р2 +… + РN
Задачи, решение которых основывается на данных уравнениях, можно разделить на две группы:
§ задачи на применение уравнения Менделеева-Клапейрона.
- задачи на газовые законы.
ЗАДАЧИ НА ПРИМЕНЕНИЕ УРАВНЕНИЯ МЕНДЕЛЕЕВА-КЛАПЕЙРОНА.
Уравнение Менделеева-Клапейрона применяют тогда, когда
I. дано только одно состояние газа изадана масса газа (или вместо массы используют количество вещества или плотность газа).
II. масса газа не задана, но она меняется, то есть утечка газа или накачка.
При решении задач на применение равнения состояния идеального газа надо помнить:
1.если дана смесь газов, то уравнение Менделеева-Клапейрона записывают для каждого компонента в отдельности.Связь между парциальными давлениями газов, входящих в смесь и результирующим давлением смеси, устанавливается законом Дальтона.
2.если газ меняет свои термодинамические параметры или массу, уравнение Менделеева-Клапейрона записывают для каждого состояния газа в отдельности и полученную систему уравнений решают относительно искомой величины.
P.S.
§ Необходимо пользоваться только абсолютной температурой и сразу же переводить значения температуры по шкале Цельсия в значения по шкале Кельвина.
§ В задачах, где рассматривается движение сосуда с газом (пузырька воздуха, воздушного шара) к уравнению газового состояния добавляют уравнения механики.
§ если между газами происходит реакция, то надо составить уравнение реакции и определить продукты реакции
ПЕРВЫЙ ТИП ЗАДАЧ: НЕТ ИЗМЕНЕНИЯ МАССЫ
Определить давление кислорода в баллоне объемом V = 1 м3 при температуре t=27 °С. Масса кислорода m = 0,2 кг.
| V = 1 м3 μ = 0,032кг/моль m = 0,2 кг t=27 °С | Т=300К | Записываем уравнение Менделеева-Клапейрона и находим из него давление, производимое газом: |
| Р-? |
Баллон емкостью V= 12 л содержит углекислый газ. Давление газа Р = 1 МПа, температура Т = 300 К. Определить массу газа.
| V = 12 л μ =0,044кг/моль Т=300К Р =1 МПа | 0,012м3 1∙106Па | Записываем уравнение Менделеева-Клапейрона и находим массу газа |
| m -? |
При температуре Т = 309 К и давлении Р = 0,7 МПа плотность газа ρ = 12 кг/м3. Определить молярную массу газа.
| V = 12 л Т=309К Р =0,7 МПа ρ = 12 кг/м3 | 0,012м3 0,7∙106Па | Записываем уравнение Менделеева-Клапейрона Так как масса газа может быть определена через плотность газа и его объем имеем: |
| μ -? | ||
Отсюда находим молярную массу газа: | ||
Какова плотность водорода при нормальном атмосферном давлении и температуре 20°С.
| V = 12 л t=20°C Р =105 Па μ =0,002кг/моль | 0,012м3 T=293К | Нормальное атмосферное давление – это давление, равное 105 Па. И эту информацию запишем как данные задачи. Записываем уравнение Менделеева-Клапейрона |
| ρ -? | ||
Так как масса газа может быть определена через плотность газа и его объем имеем: Отсюда находим плотность газа: | ||
До какой температуры Т1 надо нагреть кислород, чтобы его плотность стала равна плотности водорода при том же давлении ,но при температуре Т2 = 200 К?
| Т2=200К ρ1 = ρ2 μ1 =0,032кг/моль μ2 =0,002кг/моль | Записываем уравнение Менделеева-Клапейрона для кислорода и для водорода через плотности газов: Так как по условию давление у двух газов одинаковое, то можно приравнять правые части данных уравнений: Сократим на R и на плотность ρ (по условию плотности газов равны) и найдем Т1 |
| Т1 -? | |
В сосуде объемом 4·10-3 м3 находится 0,012 кг газа при температуре 177°С. При какой температуре плотность этого газа будет равна 6·10-6 кг /см3, если давление газа остается неизменным.
Смесь газов
В баллоне объемом 25 литров находится 20г азота и 2 г гелия при 301К. Найдите давление в баллоне.
Определить плотность смеси, состоящей из 4 граммов водорода и 32 граммов кислорода при давлении 7°С и давлении 93кПа?
Сосуд емкостью 2V разделен пополам полупроницаемой перегородкой. В одной половине находится водород массой mВ и азот массой mА. В другой половине вакуум. Во время процесса поддерживается постоянная температура Т. Через перегородку может диффундировать только водород. Какое давление установиться в обеих частях сосуда?
| μа m1 = m2 = m3 = m μв μк Т | отсек №1 отсек №2 отсек №3 Диффундирует только водород. Следовательно, после завершения установочных процессов, в отсеке I будет водород, массой на |
| РI-? РII-? | |
половину меньшей, чем была, и весь азот. А во втором отсеке только половина массы водорода. Тогда для первого отсека установившееся давление равно: Для отсека II можно так же определить установившееся давление: | |
Вакуумированный сосуд разделен перегородками на три равных отсека, каждый объемом V. В средний отсек ввели одинаковые массы кислорода, азота и водорода. В результате чего давление в этом отсеке стало равно Р. Перегородка I проницаема только для молекул водорода, перегородка II проницаема для молекул всех газов. Найти давления Р1 Р2 и Р3, установившиеся в каждом отсеке, если температура газа поддерживается постоянной и равной Т.
| μа m1 = m2 = m3 = m μв μк Р | отсек №1 отсек №2 отсек №3 После диффундирования газов через перегородки в первом отсеке окажется треть массы водорода. Во втором и в третьем отсеках будет треть водорода, половина массы кислорода и половина всей массы азота. Тогда для первого отсека установившееся давление равно: |
| Р1-? Р2-? Р3-? | |
Если до диффундирования первоначальное давление во втором отсеке было Р, то можно записать: Отсюда можно найти Находим выражение для давления во втором и в третьем отсеках | |
И тогда давление в первом отсеке равно: | |
С химическими реакциями
В сосуде находится смесь азота и водорода. При температуре Т, когда азот полностью диссоциирован на атомы, давление равно Р (диссоциацией водорода можно пренебречь). При температуре 2Т, когда оба газа полностью диссоциированы, давление в сосуде 3Р. Каково отношение масс азота и водорода в смеси?
| μа μв Т1 =Т Т2 =2Т Р1=Р Р2=3Р | mв μвmа При температуре Т параметры газов в сосуде следующие: И результирующее давление в сосуде по закону Дальтона равно: |
2Т 2Т При температуре 2Т параметры газов в сосуде следующие: И результирующее давление в сосуде по закону Дальтона равно: | |
В герметично закрытом сосуде находится 1 моль неона и 2 моля водорода. При температуре Т1=300К, когда весь водород молекулярный, атмосферное давление в сосуде Р1=105 Па. При температуре Т2=3000К давление возросло до Р2=1,5∙105 Па. Какая часть молекул водорода диссоциировала на атомы?
| ν1=1 моль ν2=2 моль Т1 =300К Т2 =3000К Р1=105 Па Р2=1,5∙105 Па | При температуре Т1 давление газа в сосуде складывается из парциальных давлений двух газов и равно: При температуре Т2 давление газа равно: |
Из уравнения (1): Из первого находим объем V: | |
В закрытом баллоне находится смесь из m1= 0,50 г водорода и m2 = 8,0 г кислорода при давлении Р1= 2,35∙105 Па. Между газами происходит реакция с образованием водяного пара. Какое давление Р установится в баллоне после охлаждения до первоначальной температуры? Конденсации пара не происходит.
| V = 25 л μ1 = 2г/моль m1 = 0,5 г μ2 = 32г/моль m2 = 8 г | В сосуде будет происходить реакция водорода с кислородом с образованием воды:
|
| Р-? | Из уравнения реакции видно, что если в реакцию вступит весь водород, то кислорода только половина |
В результате образуется ν3=0,25 молей водяного пара и останется ν4= 0,125молей кислорода. По закону Дальтона результирующее давление в сосуде равно сумме парциальных давлений Так как известно, что до реакции давление в сосуде было Р1, то для этого момента можно так же применить закон Дальтона: Решаем полученные уравнение в системе относительно неизвестного: Дата добавления: 2018-04-04; просмотров: 2754; | |
Источник
Задача
№1.
В
автомобильн6ой
шине
находится
воздух под
давлением 5,9·105
Па при
температуре
293 К. Во время
движения автомобиля
температура
воздуха
повышается
до 308 К. На
сколько
увеличится
давление воздуха
внутри шины?
Объём шины
считать
постоянным.
Р1 = 5,9·105 Па; Т1 = 293 К; Т2 = 308 К. |
ΔР – ? |
Решение:
объём шины
остаётся
постоянным, следовательно
применим
закон Шарля:
где Р2
– давление,
при котором
находится
воздух в шине
при
температуре
Т2.
Из закона
Шарля:
Увеличение
давления
определим
как разность
давлений при
температурах
Т2 и Т1:
;
Ответ:
давление в
шине
увеличится
на 3,02·104 Па.
Задача
№2.
Плотность
газа при
давлении 2·105
Па и
температуре
27°С равна 2,4 кг/м3.
Какова
молярная
масса этого
газа? Универсальная
газовая
постоянная 8,32
Дж/моль·К.
ρ1 = 2,4 кг/м3; Р = 2·105 Па; Т = 27°С = 300 К; R = 8,32 Дж/моль·К. |
μ – ? |
Решение:
запишем
уравнение
Менделеева-Клапейрона:
По
определению
плотность где m –
масса газа, V – его
объём.
Тогда откуда
Размерность: .
Ответ:
молярная
масса газа
равна
примерно 3·10-2
кг/моль.
Задача
№3.
Определить
плотность
насыщенного
водяного
пара при 27°С,
если
известно, что
его давление
при этой
температуре
равно 26,7 мм.рт.ст.
Молярная
масса пара 18·10-3
кг/моль.
Газовая
постоянная
8,З1 Дж/моль·К.
Т = 27°С = 300 К; Р = 26,7 μ = 18·10-3 R = 8,31 Дж/моль·К. |
ρ |
Решение:
запишем
уравнение
Менделеева-Клапейрона:
.
Плотность
вещества где m –
масса пара,
тогда:
откуда
.
Размерность: .
Ответ:
плотность
водяного
пара при 27°С
равна 2,6·10-2
кг/м3.
Задача
№4.
Из сосуда
откачивают
воздух. Объём
сосуда 3·10-3 м-3,
объём
цилиндра
насоса 0,5·10-3 м-3.
Каким будет
давление
воздуха в
сосуде после
пяти рабочих
ходов поршня,
если сосуд в
начале
содержал
воздух при
давлении 1,013·105
Па, а
температура
– постоянная.
V1 V2 P0 = 1,013·105Па; t° = const. |
P5 – ? |
Решение:
температура
в процессе
откачки воздуха
остаётся
постоянной,
следовательно,
при решении
задачи
необходимо
использовать
закон
Бойля-Мариотта.
Если
первоначально
воздух
занимал
объём V1, то в
конце
первого хода
поршня
воздух будет
занимать
объём V1 + V2 и
иметь
давление P1. По
закону
Бойля-Мариотта:
P0V1 = P1·(V1 + V2);
.
В начале
второго
рабочего
хода поршня
объём и
давление
воздуха
равны
соответственно
V1 и P1, в
конце V1 + V2 и P2.
Применив ещё
раз
соотношение
Бойля-Мариотта
получим:
P0V1 = P1·(V1 + V2);
.
Вообще к
концу n-го
рабочего
хода:
.
Приведём
размерность: .
Подставляя
числовые
значения:
.
Ответ:
давление
установится
равным 0,469·105
Па.
Задача
№5.
Некоторую
массу газа
при постоянной
температуре
сжимают так,
что его объём
уменьшается
в 4 раза. После
этого при постоянном
объёме
охлаждают с
77°С до 7°С.
Определите,
во сколько
раз
изменилось
давление газа.
; t1 t3 = 7°С, Т3 = 280 К. |
Решение: в
описанном
процессе
имеются три состояния,
характеризующиеся
параметрами:
|P1; V1; T1|, |P2; V2; T2| и |P3; V3; T3|.
Согласно
уравнению
Менделеева –
Клапейрона:
Так как Т1
= Т2 и , то ,
откуда
Ответ:
давление
возросло в 3,2
раза.
Задача
№6.
Открытый
сосуд нагрет
до
температуры
450°С. Какая
часть массы
воздуха
осталась в
нём, по
сравнения с
тем
количеством,
какое в нём было
при 27°С? Расширением
сосуда
пренебречь.
t1 = 27°С, Т1 = 300 К; t2 = 450°С, Т2 = 723 К. |
Решение:
термодинамическое
состояние газа
описывается
уравнением
Менделеева-Клапейрона.
Так как масса
воздуха в
сосуде меняется,
то применим
уравнение Менделеева-Клапейрона
для каждой
массы до и
после
нагревания:
1) –
до
нагревания;
2) –
после
нагревания,
где m1 и m2 –
массы
воздуха в
сосуде,
соответственно,
до и после
нагревания.
Поделив
второе уравнение
на первое,
получим:
.
Подставив
значения: .
Ответ:
после
нагревания
осталась 0,415-я
часть воздуха.
Задача
№7.
Определить
плотность
смеси,
состоящей из
4·10-3 кг
водорода и 32·10-3
кг
кислорода
при
температуре
280 К и давлении
9,3·104 Па.
m1 = 4·10-3 кг; m2 = 32·10-3 кг; μ1 = 2·10-3 μ2 = 32·10-3 T = 280 К; Рсм R = 8,31 Дж/моль·К. |
ρсм |
Решение:
плотность
смеси
определяется
как
отношение
всей массы
газа к
объёму,
занимаемому
газом:
,
где m1 –
масса
водорода; m2 –
масса
кислорода; V –
объём
занимаемый
смесью.
Объём
занимаемый
смесью можно
определить,
используя
закон
Дальтона,
закон
Менделеева-Клапейрона:
,
где P1 –
парциальное
давление
воздуха в
смеси;
P2 –
парциальное
давление
кислорода в
смеси.
Из
полученного
уравнения
определяем
объём,
занимаемый
смесью
водорода и
кислорода:
Таким
образом,
плотность
смеси
определяется
соотношением:
Проверка
единиц
измерения:
Ответ:
плотность
смеси равна 0,48
кг/м3.
Задача
№8.
Из
кислородного
баллона
емкостью 25 л
при
температуре
17°С
израсходовали
часть кислорода,
причем
давление в
баллоне
понизилось
на 0,4 МПа.
Определить массу
израсходованного
кислорода.
V = 25 л T = 17°С = 290 К; ΔP = 0,4 МПа = 4·105 μ = 32·10-3 | |
Δm – ? |
Решение:
кислород
имеет два
состояния.
Для первого
состояния
параметры
газа:
,
для
второго
состояния: .
Записываем
уравнения
для этих
состояний, имея
в виду, что
если в первом
состоянии
масса m1, то во
втором она
равна:
m2 = m1 – Δm,
где Δm –
масса израсходованного
кислорода.
; P2 = P1
– ΔP;
; m2 = m1
– Δm.
Решаем
систему,
определяя Δm:
;
;
.
Подставим
числовые
значения:
Проверим
размерность:
Ответ:
масса
израсходованного
кислорода Δm = 0,133 кг.
Задача
№9.
Какие
изменения
происходят с
параметрами
состояния
идеального
газа при
переходе из
состояния 1 в
состояние 2?
Масса газа
постоянна.
Ответ:
изохорное
охлаждение
(т.к. V =
const, а P
падает).
Задача
№10.
Резиновый
мяч содержит 2 л
воздуха,
находящегося
при
температуре
20°С и под
давлением 780 мм.рт.ст.
Какой объем
займет
воздух, если
мяч будет
опущен в воду
на глубину 10м?
Температура
воды 4°С.
t1 = 20°С, Т1 = 293 К; V1 = 2 Р1 t2 = 4°С, Т2 = 277 К; ρ = h = 10 м. |
V1 – ? |
Решение:
давление
воздуха под
упругой оболочкой
мяча,
находящегося
на глубине h,
равно
давлению в
воде на этой
глубине:
P2 = P1 + ρgh.
Подставляя
это
соотношение
в уравнение состояния,
получим:
.
Откуда ; V2 = 9,8·10-4 м3.
Ответ:
воздух
займёт объём
9,8·10-4 м3.
Задача
№11.
Баллон
содержит
сжатый
воздух при 27°С
и давлении 40
ат. Каково
будет давление,
когда из
баллона
будет
выпущена половина
массы газа и
температура
понизится до
12°С?
t1 = 27°С, Т1 = 300 К; t2 = 12°С, Т2 = 285 К; Р1 |
Р2 – ? |
Решение:
уравнение
Менделеева-Клапейрона
для каждого
состояния
газа имеет
вид:
,
По
условию: .
Из этих
уравнений: ; Р2
= 1,9·105 Па.
Ответ:
установится
давление 1,9·105
Па.
Задача
№12. На рис. а,
дан график
изменения
состояния
идеального
газа в
координатах
P, V.
Представить
этот цикл в
координатах
Р, Т,
обозначив
соответствующие
точки.
Решение:
при решении
этих задач
используются
газовые
законы.
Обозначим
параметры
каждого
состояния:
1 – P1, V1, T1; 2
– P1, V2, T2;
3
– P2, V2, T3; 4 – P2, V1, T4.
Процесс
1 – 2: P = const,
.
С учетом
этого
процесс 1 – 2 в
координатах P, T
изображаем
следующим
образом:
указываем координаты
точки 1 (T1 – произвольно;
P1 – из
рис. а),
координаты
точки 2 ( , где V1, V2 из
рис. а); затем
эти точки
соединяем
(рис. б).
Процесс 2 –
3: V =
const, .
Координаты
точки 3: T3 – на
пересечении
изохоры 2 – 3
(прямая через
начало 0) и
горизонтальной
изобары P1; P2 – из
рис. а.
Процесс 3 –
4: P =
const, .
Процесс 4 –
1: V =
const, .
Координаты
точки 4: T4 – на
пересечении
изохоры 1 – 4
(прямая через
начало 0) и
изобары P1; P2 – из
рис. а.
Источник
Влажность воздуха
Насыщенный пар
Парциальное давление
Абсолютная влажность
Относительная влажность
Водяные пары
Точка росы
Максимальная влажность
Туман
Теория
В воздухе, как мы знаем, существуют расстояния между молекулами. Возьмем гипотетический шар 1м³ с температурой 40 °С и заполним его 4 молекулами воды.
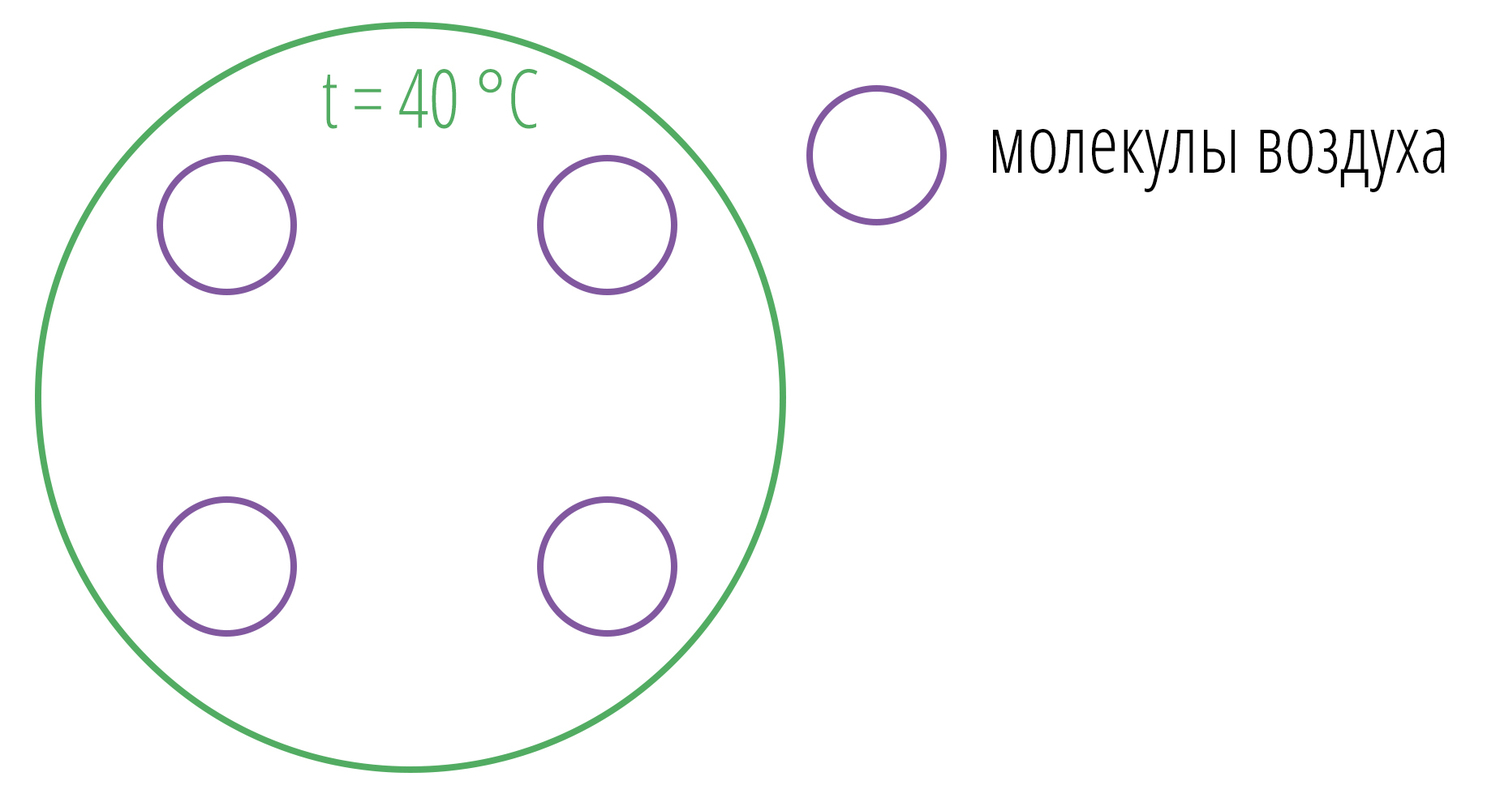
Между молекулами остается пространство, которое заполняется молекулами воды, пусть остается 5 свободных мест.
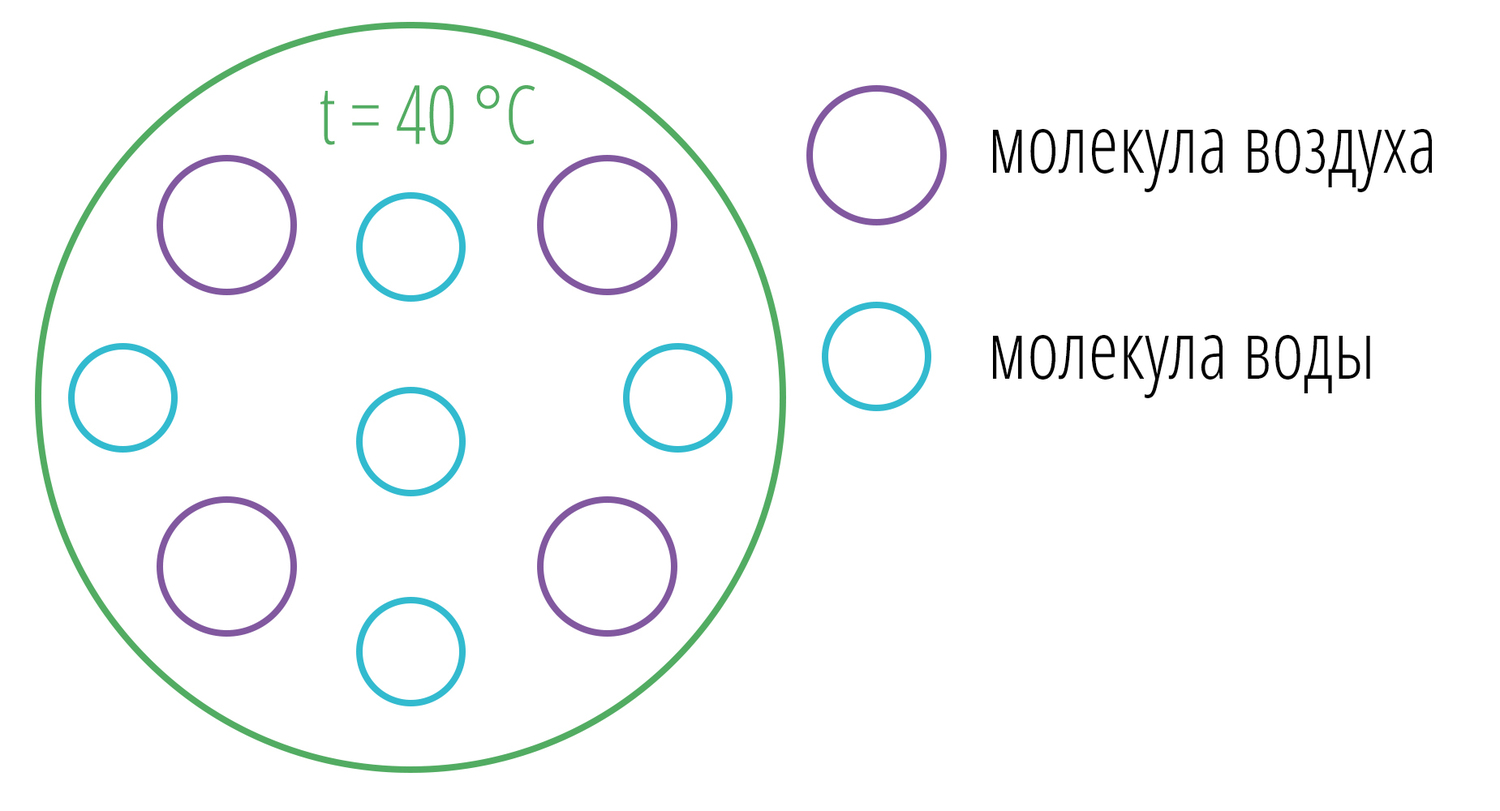
Если все 5 «вакатных» мест заняты, то относительная влажность составляет 100% (5 из 5). Такое состояние еще называют насыщенным паром.
Если нашлось только 3 молекулы воды, то относительная влажность составляет 60% (3 из 5).
Относительная влажность — величина, показывающая насколько далек пар от насыщения (сколько молекул воды могут занять свободные места).
Если же теперь взвесить первоначальный шар только с воздухом, а затем с воздухом и водой, то изменение массы и будет абсолютной влажностью
Абсолютная влажность — масса молекул воды при данной температуре.
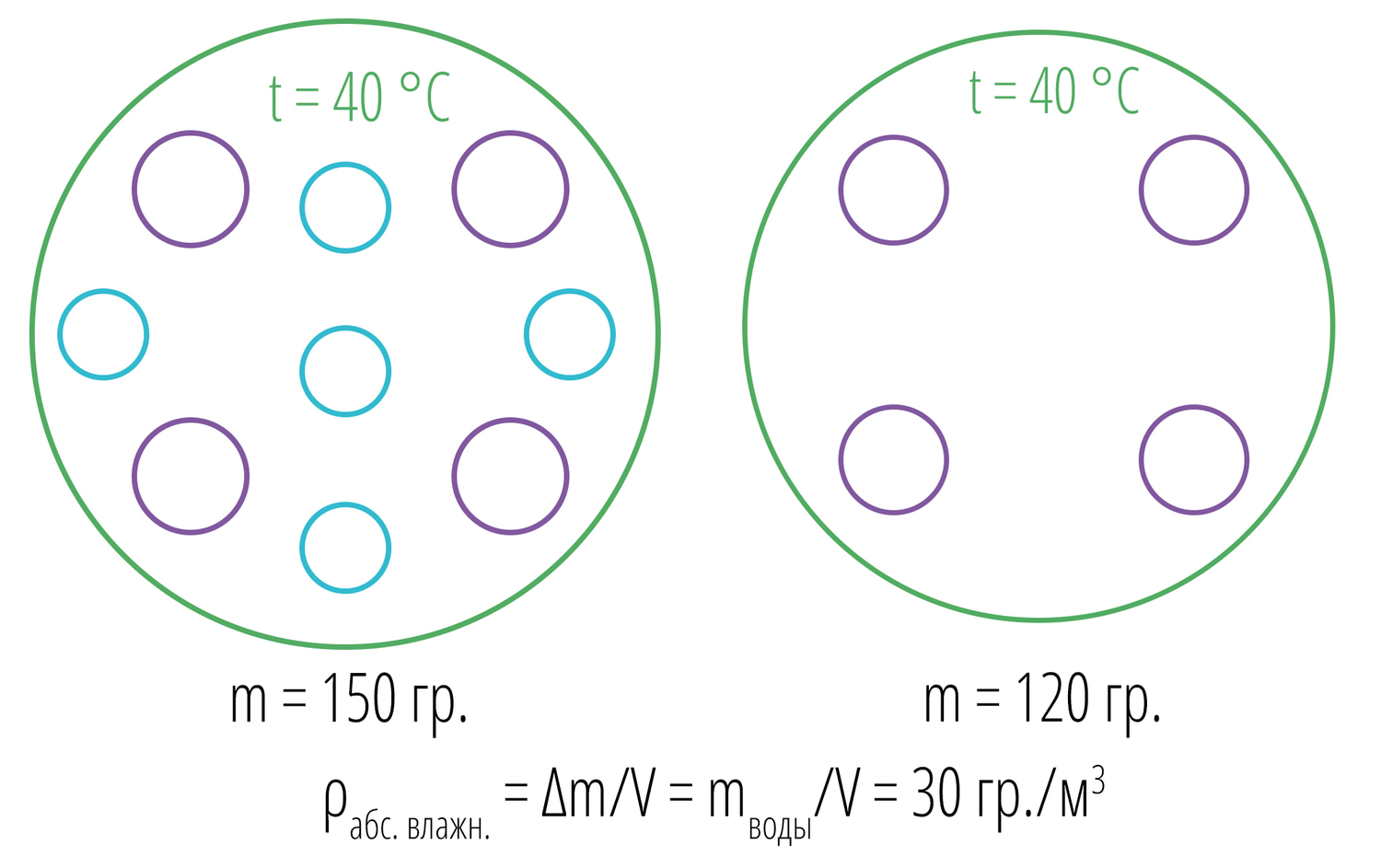
Точка росы — это температура, при которой водяной пар становится насыщенным (не осталось свободного места для молекул воды).
Надеюсь, ты читал внимательно и заметил, что все сравнения мы проводили при одной температуре. Можно находить относительную и абсолютную влажность только при одинаковой температуре!
При увеличении температуры растет абсолютная влажность. При T↑ Eк↑, значит, расстояние между молекулами воздуха увеличивается, тогда для молекул воды места будет больше. С ростом температуры увеличивается максимальная влажность.
Максимальная влажность — максимальное количество газообразной воды, которое может поместиться в заданном объеме.
Туман
Тума́н — атмосферное явление, скопление воды в воздухе, когда образуются мельчайшие продукты конденсации водяного пара.
Почему слева на фото есть туман, справа его нет?
Туман возникает не всегда при низких температурах. Если на улице температура низкая, это не значит, что там появится туман. Туман возникает при резком спаде температур. Днем, например, температура была высокой, поэтому много влаги испарилось в воздух. Ночью температура быстро опустилась — той влаги, что содержалась в воздухе до падения температуры (и была незаметна), становится слишком много — воздух становится перенасыщенным водой, и часть ее оседает в виде росы, а часть находится во взвешенном состоянии в воздухе. Это и есть сам туман.
Задачи
Для решения задач требуется две дополнительные формулы, помимо основных формул МКТ:
Плотность пара делим на плотность насыщенного пара при данной температуре или давление пара делим на давление насыщенного пара при данной температуре.
В скобочках написаны советы, когда какой формулой пользоваться:
Задача №1 Плотность водяного пара при температуре 25 °С равна 23 г/м³. Насыщенная это пар или ненасыщенный?
Насыщенный пар имеет относительную влажность φ = 100%. Для того, чтобы определить это, нужно открыть таблицу зависимости плотности насыщенного пара от температуры:
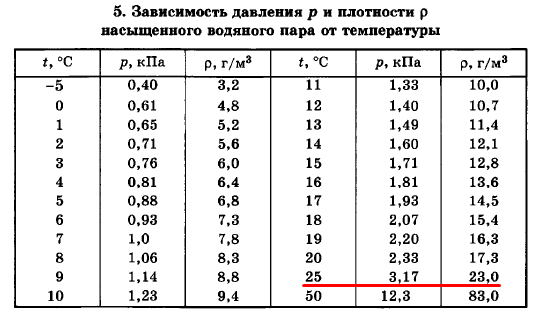Ответ: насыщенный.
Задача №2 Относительная влажность воздуха равна 42 %, парциальное давление пара при температуре 20 °С равно 980 Па. Каково давление насыщенного пара при заданной температуре?
Парциа́льное давление — давление отдельно взятого компонента газовой смеси. Воздух состоит из множества газов, давление одного из газов равно 980 Па.
Нужно найти давление насыщенного пара, значит, воспользуемся формулой относительной влажности через давления:
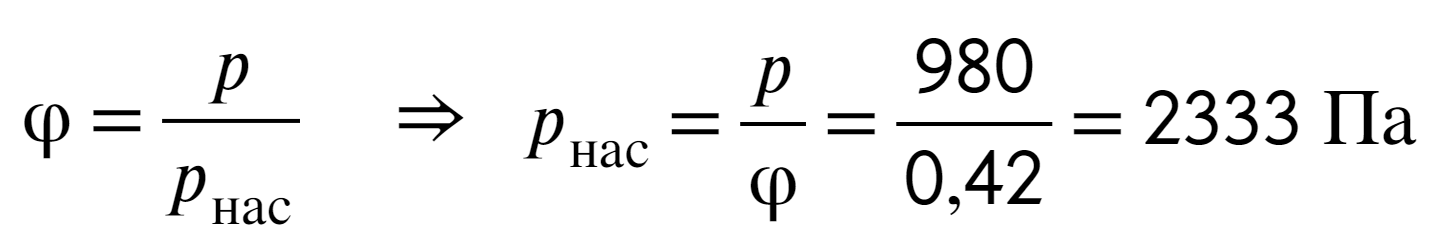
Температура не меняется, значит, ее никак использовать не нужно.
Ответ: 2333 Па.
Задача №3 На рисунке изображена зависимость давления p насыщенного водяного пара от температуры t. Точкой A на этом графике обозначено состояние пара, находящегося в закрытом сосуде. Чему равна относительная влажность воздуха в этом сосуде?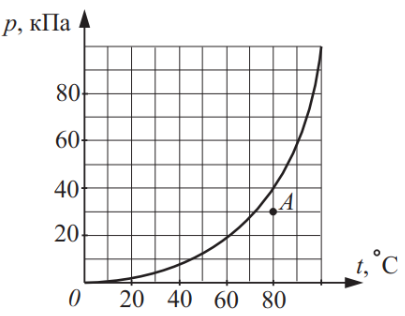
О том, что показано на графике: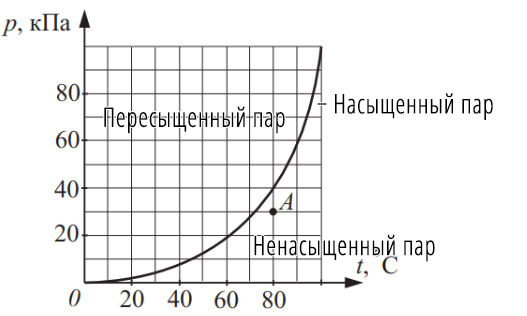 
Что самое главное при нахождение относительной влажности? Конечно, одинаковая температура!
Сравниваем давления только при одинаковой температуре:
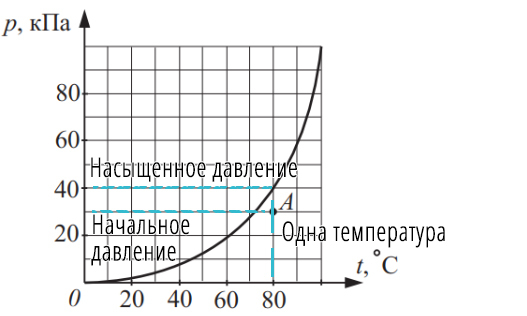
Начальная температура 80 °С и начальное давление 30 кПа, а давленые насыщенного пара при 80 °С 40 кПа, тогда:
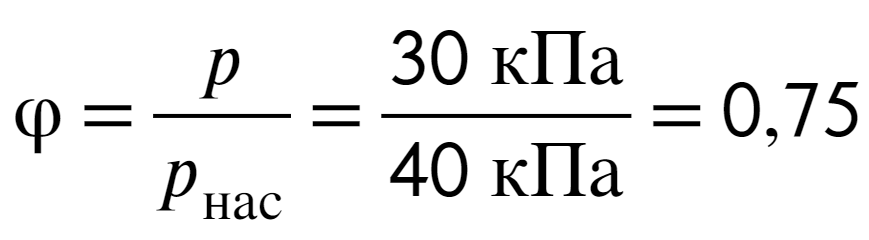Ответ: 0,75
Задача №4 При температуре t = 20 °С относительная влажность в комнате φ1 = 20%. Какую массу воды нужно испарить для увеличения влажности до φ2 = 50%, если объем комнаты V = 40 м³? Плотность насыщенных паров воды при температуре t = 20 °С равна ρ₀ = 1,73⋅10⁻² кг/м
Комнату можно представить в виде закрытого сосуда, значит, для нахождения относительной влажности воспользуемся формулой через плотность:
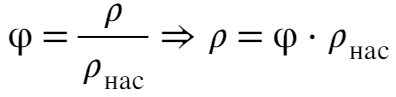Изменение массы (сколько нужно испарить) найдем по определению:
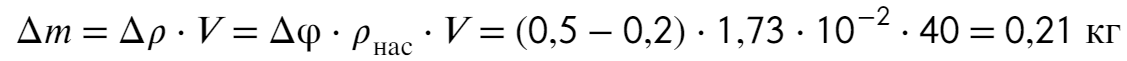Ответ: 0,21 кг
Задача №5 В сосуде объёмом 3 л при температуре +70 °C находится смесь воздуха с водяными парами. Давление в сосуде равно 99,2 кПа, относительная влажность воздуха 50 %. Давление насыщенного водяного пара при данной температуре равно 31,1 кПа. Какое количество воздуха находится в сосуде?
Как вещи постепенно все труднее упаковывать в чемодан, так и давление все труднее и труднее повышать.
По закону Дальтона давление смеси газов равно сумме всех отдельных газов (Как объем полностью забитого чемодана равен сумме объемов всех вещей в нем).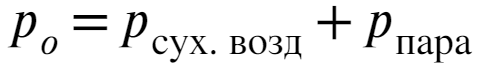
Давление насыщенных водяных паров и относительная влажность известны, тогда можно найти давление паров: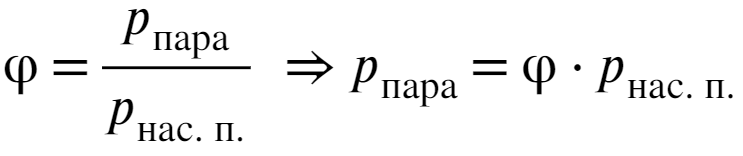
Выразим давление сухого воздуха и представим его через уравнениеие Менделеева-Клапейрона: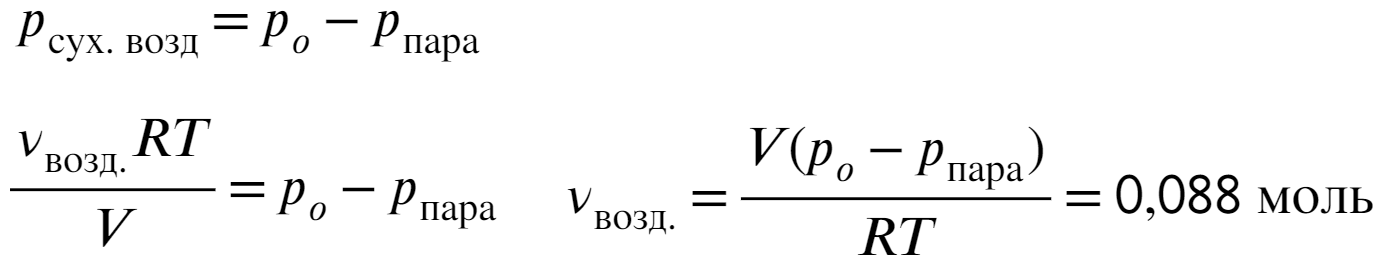
Ответ: 88 милимоль
Задача №6 В закрытом сосуде объёмом 6 л при температуре +17 °C находится воздух, имеющий влажность 25%. Давление насыщенных паров воды при этой температуре равно 1875 Па. Какую массу воды надо испарить в сосуде при данной температуре для того, чтобы влажность воздуха стала равна 100%? Ответ выразите в миллиграммах и округлите до целого числа.
25% влажности уже есть, нам осталось добавить еще 75% и найти, сколько нужно добавить давления:
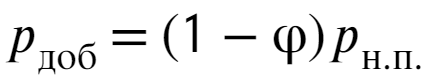
Остается выразить массу из уравнения Менд.-Кл. и подставить числа:
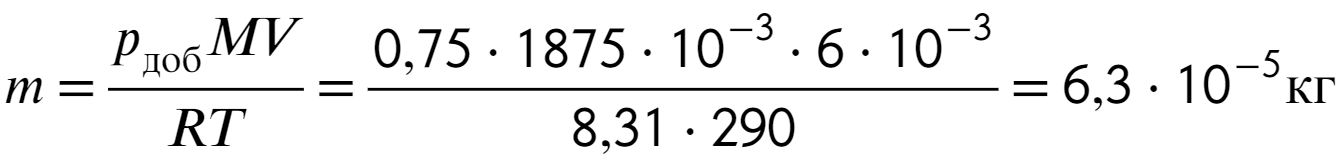
Ответ: 63 мг
Задача №7 В комнате размерами 4×5×3 м, в которой воздух имеет температуру 10 °C и относительную влажность 30 %, включили увлажнитель воздуха производительностью 0,2 л/ч. Чему станет равна относительная влажность воздуха в комнате через 1,5 ч? Давление насыщенного водяного пара при температуре 10 °C равно 1,23 кПа. Комнату считать герметичным сосудом. (ЕГЭ 2019)
Для начала найдем, сколько обрзовалось воды за 1,5 часа с мощностью 0,2 л/ч.
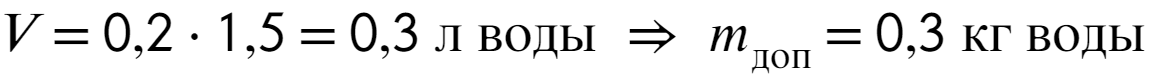Начальное давление в комнате можно найти уже по известной нам формуле:
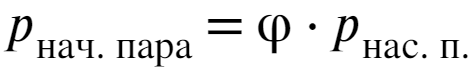
С этими знаниями через уравнение Менд.-Кл. найдем начальную массу воды в газообразном состоянии:
Через 1,5 часа в воздухе окажется почти полкило воды, найдем давление:
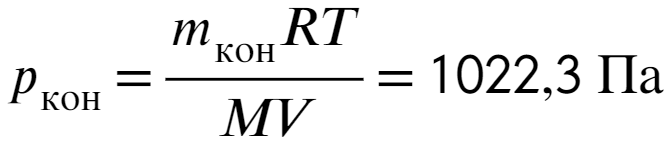
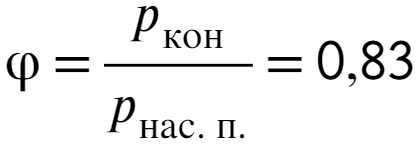Ответ: 83%
Задача №8 Два сосуда объёмами 20 л и 30 л, соединённые трубкой с краном, содержат влажный воздух при комнатной температуре. Относительная влажность в сосудах равна соответственно 30% и 40%. Если кран открыть, то какой будет относительная влажность воздуха в сосудах после установления теплового равновесия, считая температуру постоянной? (ЕГЭ 2015)
В данной задаче говорится о закрытых сосудах, значит, через какую формулу будем выражать относительную влажность? Да, через плотность!
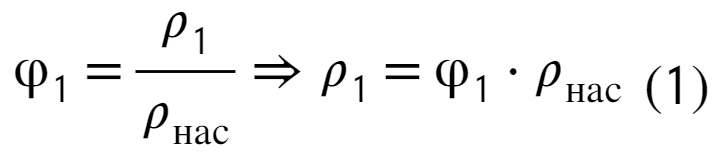
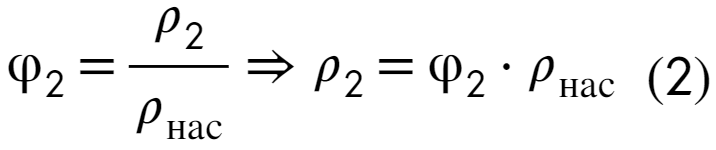
Плотность можно найти через отношение массы к объему, а дальше расписываем как сумму масс и объемов:
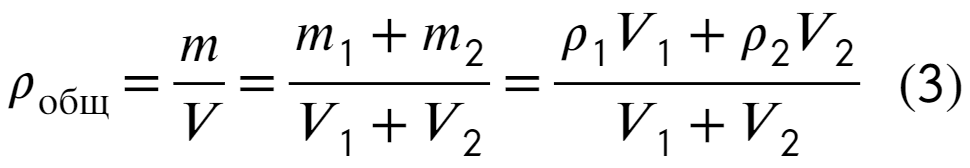
Остается соединить выведенные соотношения (1), (2), (3), сократить плотность насыщенных паров и получить ответ: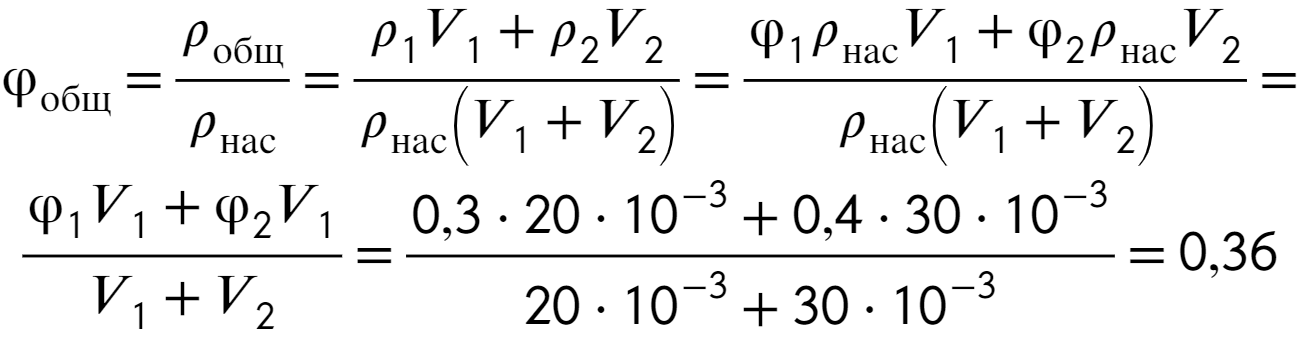
Ответ: 36%
Задача №9 После тёплого летнего дождя относительная влажность воздуха уповерхности земли достигла 100%. При этом плотность влажного воздуха (масса пара и воздухав 1 м³) оказалась равной ρ = 1171 г/м³, его давление p = 100 кПа и температура 22 °C. Найти по этим данным давление насыщенного водяного пара при температуре 22 °C. Молярная массавоздуха Mв = 29 г/моль. (МФТИ 1999)
По закону Дальтона запишем, что плотность и давление влажного воздуха находятся как сумма сухового воздуха и пара:
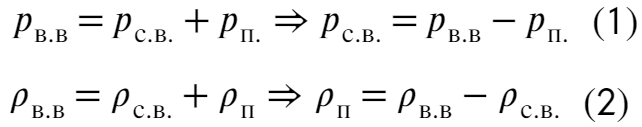Выразим через уравнение Менд.-Кл. плотность сухового воздуха через давление:
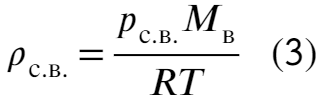
А теперь наоборот выразим давление пара через плотность:
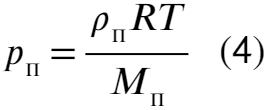
Подставляя теперь в ур-ие (4) ур-ие (2), ур-ие (3) и затем ур-ие (1) получим уравнение относительно давления пара: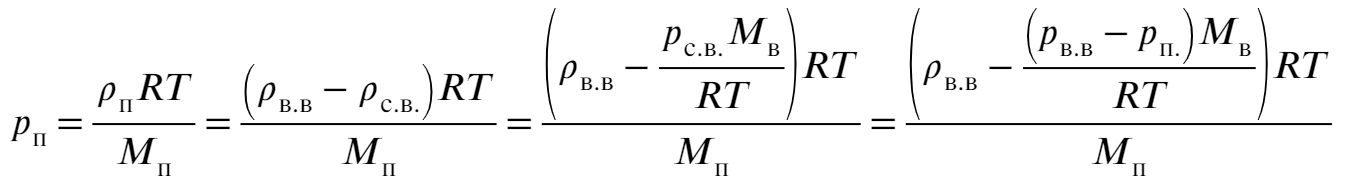
Остается выразить и подставить значения:
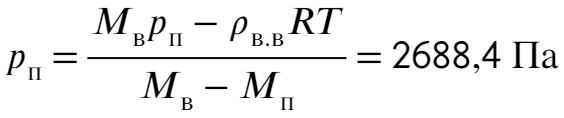Ответ: 2,7 кПа
Хорошая тема, и в баньку с ней сходить можно, и с туманом познакомиться. Не знаю, чего она так вам не нравится. Помни, какую формулу и где лучше применить — это на порядок упростит решение задач!
В качестве закрепления материала решите несколько похожих задач с ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
Источник