Сосуд обманувший силу тяжести

История открытия
В древних Сиракузах жил инженер, математик и физик по имени Архимед. Образование он получил отличное, изобретения его ценились и в средствах он не нуждался. И периодически к нему обращались сильные мира для решения всяких сложных задач. И одной из таких задач было определить подлинность короны царя Гиерона.
Казалось бы, что в этом сложного?
Используй формулу
ρт = mт / Vт (1).
Раздели mт массу слитка, что был выдан ювелиру на объем короны Vт, получишь плотность короны ρт. Сравни полученный результат с известной плотностью золота, и дело в шляпе. А ювелир получит либо плату за работу, либо близкое знакомство с придворным палачом.
Однако эта формула хорошо работает с объектами простой формы: шар, куб, параллелепипед. А мы то помним, что исследуем корону, у которой множество зубцов, выпуклостей и ажурных плетений.
Как можно определить объем предмета столь сложной формы? Не знаете? Вот и Архимед тоже не знал.

Физика. 7 класс. Учебник
Учебник соответствует Федеральному государственному образовательному стандарту основного общего образования. Большое количество красочных иллюстраций, разнообразные вопросы и задания, а также дополнительные сведения и любопытные факты способствуют эффективному усвоению учебного материала.
Купить
Долгое время ученый думал над задачей, и в один из дней, в задумчивости опускаясь в наполненную водой ванну, обратил внимание, что часть воды выплеснулась через край. Современники рассказывают, что именно в этот момент Архимед закричал: «Эврика!», что по-гречески значит «Нашел!» и, даже не одеваясь, побежал в царский дворец.
Еще пару дней понадобилось исследователю, чтобы изобрести прибор, с помощью которого он мог бы измерить объем воды, вылившейся при погружении короны. Этот прибор, названный впоследствии ведерком Архимеда, можно увидеть на странице 145 учебника «Физика 7 класс» под редакцией А.В.Перышкина.
Затем, с помощью опытов с золотыми и серебряными слитками, доказать, что объем жидкости равен объему слитка, а следовательно будет равен и объему короны. И последним этапом определить плотность короны.
Говорят, что царь был прав в своих подозрениях, и ювелир был нечист на руку. А всю плату, что причиталась за корону мастеру, получил Архимед.
Действие жидкости и газа на погруженное в них тело
Что же открыл Архимед благодаря своим опытам?
Ученый определил некую силу, которая действую в обратном направлении силе притяжения и позволяет предметам плавать в воде и воздухе. Эту силу по праву назвали силой Архимеда или выталкивающей силой.
Определение закона Архимеда: тело погруженное в жидкость, теряет в своем весе столько, сколько весит вытесненная им жидкость.
Формулы
На планете Земля на все предметы действует сила земного притяжения. Для объектов на земной поверхности силу притяжения можно рассчитать по формуле:
Fт = mтg, (2)
где mт — масса тела, а g — ускорение свободного падения, равное 9,8 м/с2.
Когда же объект погружается в жидкость или газ, на него начинает действовать выталкивающая сила или сила Архимеда, которая рассчитывается по формуле:
FА = mжg, (3)
где mж — масса жидкости, вытесненной целым объектом или его частью, находящейся в жидкости.
Массу вытесненной жидкости в свою очередь можно определить используя формулу:
mж = ρжVж, (4)
и соответственно преобразовать формулу закона Архимеда:
FА = ρжVжg. (5)
Как же соотносятся между собой сила тяжести и сила выталкивания. Все просто:
- если сила притяжения больше силы выталкивания, предмет утонет;
- если силы примерно равны — предмет будет плавать в толще жидкости или газа;
- а если сила выталкивания больше силы притяжения, предмет всплывет.
Многочисленные опыты, благодаря которым мы можем пользоваться формулами силы выталкивания, подробно разобраны в § 50 учебника «Физика 7 класс» под редакцией А.В.Перышкина.
Несмотря на то, что Архимед впервые открыл силу выталкивания в воде, сила Архимеда характерна также и для газов, и именно благодаря ей смог подняться в воздух первый воздушный шар, а вдохновленный и восхищенный этим событием писатель Жюль Верн написал свой роман «Вокруг света за 80 дней».
А теперь давайте поможем царю решить его задачу с короной.
Предположим, что корона царя Гиерона в воздухе весит 22 Н, а в воде 19,75 Н, вычислите плотность вещества короны.
Как мы узнали в начале статьи, плотность вещества находится по формуле:
ρт = mт/Vт. (1)
Глядя на формулу, понимаем, что для решения задачи нам не известны ни масса короны, ни ее объем.
Из предыдущего курса физики (§ 27 учебника «Физика 7 класс» под редакцией А.В.Перышкина.), помним, что для неподвижного тела вес P равен силе тяжести Fт и рассчитывается по формуле:
P = Fт = mтg, (2)
где g — ускорение свободного падения и его значение равно g = 9,8 Н/кг. Однако, если не требуется большая точность в расчетах, значение можно округлить до 10 Н/кг
Зная вес короны в воздухе, мы используя формулу (2) можем найти массу короны.
Pт = Fт = mтg,
Мы также знаем, что вес тела в воде отличается от веса тела в воздухе на силу Архимеда.
FA = 22 — 19,75 Н = 2,25 Н
Согласно формуле (5) сила Архимеда равна FА = ρжVжg
где ρж = ρводы = 1000 кг/м3
Из нее находим объем вытесненной жидкости и соответственно объем короны
Остается финальный штрих: рассчитать плотность.
ρт = mт/Vт
ρт = 2,2 кг / 0,000225 м3 = 9778 кг/м3 или 9,8 г/см3
Зная, что плотность золота 19,3 г/см3 или 19 300 кг/м3, можем сказать, что корона царя Гиерона сделана из какого-то сплава, но не из чистого золота. Увы, царь был прав, подозревая мастера в нечестности. И мне даже немного жаль нерадивого ювелира. Ведь никто не любит, когда воруют его собственность, а цари особенно.
Теперь попробуйте самостоятельно решить задачу № 5 на странице 147 учебника «Физика 7 класс» под редакцией А.В.Перышкина.
Методические советы
Тест «Закон Архимеда»
1. Сила Архимеда это:
- сила, с которой Архимед передвигал ванну;
- сила, которая поднимает вверх тело находящееся в жидкости или газе; (+)
- сила мышц Архимеда;
- сила, с которой твердое тело действует на поверхность.
2. Сила Архимеда действует:
- на тела погруженные только в газ;
- на тела погруженные только в жидкость;
- на тела погруженные в газ или в жидкость; (+)
- на тела находящиеся в невесомости.
3. Чему равно ускорение свободного падения g?
- 9,8 м/с3;
- 9,8 Н/кг; +
- 9,8 км/ч;
- 8,9 м/с2.
4. К пружине подвешено некое тело. Если тело погрузить в емкость с жидкостью, что произойдет с пружиной?
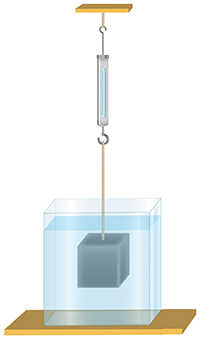
- растянется больше;
- сожмется; (+)
- не изменится;
- зависит от веса тела.
5. Два друга пошли плавать в реке. Один из них при погружении вытесняет объем 60 дм3, второй 40 дм3. На кого из ребят будет действовать большая сила Архимеда?
- на того, кто лучше умеет плавать;
- на того, кто вытеснил больше воды; (+)
- на того, то не умеет плавать;
- на того, кто вытеснил меньше воды.
6. Формула силы выталкивания это:
- FА = ρжVжg; (+)
- FА = ρтVжg;
- FА = ρжVтg;
- FА = mтg.
7. Если сила тяжести больше силы Архимеда, тело:
- взлетит;
- всплывет;
- утонет; (+)
- поплывет.
8. 4 одинаковых стальных шарика погрузили в 4 разные жидкости: чистая вода, вода мертвого моря, бензин, оливковое масло. В какой жидкости сила выталкивания будет наименьшей?
Плотность масла 915 кг/м3, плотность бензина 750 кг/м3.
- бензин; (+)
- вода Мертвого моря;
- оливковое масло;
- чистая вода.
9. Сила тяжести зависит:
- от плотности жидкости;
- от вытесненного объема жидкости;
- от массы тела; +
- от времени нахождения тела в жидкости.
10. В двух емкостях плавают два шарика равного объема. Одинакова ли сила выталкивания?
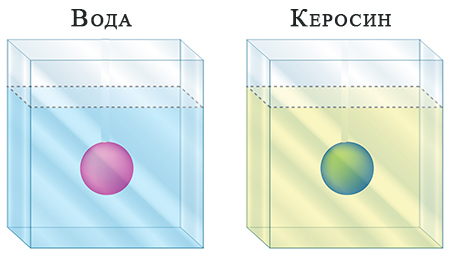
- одинакова, т.к. объем шариков одинаков;
- сила выталкивания больше в емкости с керосином, потому что плотность меньше воды;
- сила выталкивания больше в емкости с водой, потому что ее плотность больше керосина. (+)
#ADVERTISING_INSERT#
Источник
#хакнем_физика ???? рубрика, содержащая интересный, познавательный контент по физике как для школьников, так и для взрослых ????
Если решая математические задачи, следует руководствоваться только условиями, в том числе и неявно заданными (например: находя градусную меру одного из смежных углов в случаях, когда известна градусная мера другого, непременной частью условия является значение суммы градусных мер смежных углов, равной 180 град.), то при решении физических задач следует учитывать ВСЕ физические явления и процессы, влияющие на результат рассматриваемой в задаче ситуации.
Вот для примера известная и часто встречающаяся во многих учебниках и сборниках задач, в том числе и олимпиадных (и не только для семиклассников) по физике.
ЗАДАЧА
В стакане с водой плавает кусок льда. Изменится ли уровень воды, когда лёд растает?
Прежде чем продолжить чтение, предлагаю читателю дать (хотя бы для себя) обоснованный ответ на вопрос задачи…
В «Сборнике вопросов и задач по физике» [Н.И. Гольдфарб, изд. 2, «Высшая школа», М.: 1969] эта задача, помещённая как часть № 10.7 на стр. 48, на стр.193 приводится ответ:
«Лёд вытесняет воду, вес которой равен весу льда. Когда лёд растает, образуется такое же количество воды, поэтому уровень не изменится».
Такой же ответ приводится и во многих других сборниках…
А вот в популярнейшем и по сей день, выдержавшим множество изданий трёхтомнике «Элементарный учебник физики» под редакцией академика Г.С. Ландсберга [т. I, изд. 7, стереотипное, «Наука», М.: 1971] ответа на эту задачу (№ 162.2, стр. 351) не приводится. И это не случайно!
Что же не учтено в вышеприведённом ответе? Правильно! Не учтено, что при таянии льда вода в стакане охлаждается — именно поэтому мы и бросаем туда кусочек льда!
Вот как должен выглядеть правильный ответ:
«При таянии льда вода в стакане охлаждается. При охлаждении все вещества уменьшаются в объёме. Однако вода, единственная из всех известных веществ, имеет наибольшую плотность при температуре +4 град. С, а это значит, что при дальнейшем охлаждении данная масса воды увеличивается в объёме, что, как мне это было известно из курса природоведения в 5 классе (1961/1962 учебный год), является условием сохранения жизни на Земле, поскольку позволяет достаточно глубоким водоёмам не промерзать до самого дна!).
При этом возможно три варианта развития ситуации:
I. Если температура воды до начала таяния льда была выше 4 град. С и, хотя и понизилась после таяния льда, но осталась выше этой температуры, то уровень воды в стакане уменьшится.
II. Если температура воды до начала таяния льда была ниже 4 град. С, а после таяния льда ещё и уменьшилась, то уровень воды в стакане увеличится.
III. В случае, когда начальная температура воды была выше 4 град. С, а после того как лёд растаял, оказалась ниже этой температуры, то об уровне ничего определённого сказать нельзя — нужны конкретные данные о температуре и массе воды и льда, чтобы дать точный ответ на вопрос задачи!».
С этой задачей связана для меня одна интересная история.
Лет 15 назад во дворе дома, в котором я живу, ко мне с грустным выражением лица подошёл паренёк по имени Серёжа и попросил помочь подготовиться к предстоящей ему завтра апелляции по физике в нашем Политехническом институте (ныне Технический университет).
Поскольку времени было слишком мало, то я ограничился советом: если, по его мнению, апелляция пройдёт не очень удачно, и надежды исправить тройку на вступительном экзамене не будет, то попросить экзаменатора ответить на вопрос этой задачи и заставил его дословно вызубрить приведённый выше ответ и даже отработал с ним интонацию изложения этого ответа. На следующий вечер он подошёл ко мне с достаточно счастливым видом.
Вот его рассказ, каким я его запомнил:
«Всё получилось так, как Вы и хотели. Апелляцию проводили два человека: профессор и ассистент кафедры общей физики института. Мне выпало общаться с ассистентом, а профессор в это время общался с другим абитуриентом.
В ответ на мою просьбу ответить на мой вопрос ассистент слегка улыбнувшись сказал: «Пожалуйста…».
«После того, как я проговорил условие задачи, ассистент, широко улыбнувшись, произнёс: «Ну, это известная задача. Уровень воды не изменится — это следует из закона Архимеда: плавающий лёд вытесняет массу воды, равную массе льда. Образовавшаяся при таянии льда вода заполнит тот объём, который занимал в воде плавающий лёд…».
«Позвольте с Вами не согласиться», — начал я и затем совершенно спокойно слово в слово пересказал заготовленный нами ответ…
В это время профессор жестом остановил своего абитуриента и стал внимательно меня слушать…
Когда я закончил, возникла небольшая пауза…Профессор, обращаясь к ассистенту спросил: «Что скажешь?».
«Кажется, всё верно», — неуверенно ответил тот, на что профессор сказал, что никогда ещё не слышал столь аргументированного ответа, после чего, уже обращаясь ко мне, добавил: «Молодой человек, мы, к сожалению, не можем поднять Вам оценку сразу на два балла, но четвёрку Вы очевидно заслужили!»».
Мне остаётся лишь добавить, что Серёжа был зачислен студентом!…
Наши читатели могут поделиться своим мнением по поводу решения задачи. Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_физика
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Другие статьи автора:
Вы читаете контент канала “Хакнем Школа”. Подпишитесь на наш канал, чтобы не терять его из виду.
Источник
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Закон Архимеда
На погружённое в жидкость или газ тело действует выталкивающая сила, и равная весу среды, объём которой равен объёму тела.
Выталкивающая сила (сила Архимеда) равна
[F_A=rho_text{ж} g V_text{пчт}] где (displaystyle V_text{пчт}) — объём погружённой части тела, (displaystyle rho_text{ж}) — плотность жидкости.
Плавание тел
Рассмотрим тело плотности (rho) и жидкость плотности (rho_0). Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести (mg) и архимедова сила (F_A). Если объём тела равен V, то
[mg=rho g V,] [F_A=rho_0 g V]
Имеются три возможности дальнейшего движения тела.
Сила тяжести больше архимедовой силы: (displaystyle mg > F_A), или (displaystyle rho>rho_0). В этом случае тело тонет.
Сила тяжести равна архимедовой силе: (displaystyle mg = F_A), или (displaystyle rho=rho_0). В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
Сила тяжести меньше архимедовой силы: (displaystyle mg < F_A), или (displaystyle rho<rho_0). В этом случае тело всплывает, достигая поверхности жидкости.
Таким образом, условие плавания тела можно записать в виде неравенства (displaystyle rholeq rho_0).
Два жестко связанные друг с другом одинаковых бруска, имеющие толщину (h=5) см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.)
Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
(displaystylerho_1) – плотность материала, из которого изготовлены бруски, а (displaystyle V) – объем двух брусков. Тогда масса этих брусков будет равна [displaystyle m=rho_1V] Сила, с которой льдинки действуют на воду, равна силе тяжести [displaystyle F=mg=rho_1Vg] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда [F_text{Арх}=rho gfrac{V}2,] где (displaystyle rho) – плотность воды, (displaystyle frac{V}2) – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: [rho_1Vg=rho gfrac{V}2,] откуда (displaystyle rho_1=dfrac{rho}2,) то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину [frac72h=3,5cdot5text{ см}=17,5 text{ см}.] Глубина увеличится на (displaystyle 17,5 -5=12,5) см.
Ответ: 12,5
Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна (displaystyle rho_text{ ал}=2700 text{ кг}/text{м}^3. ) Какова длина ребра куба, если выталкивающая сила равна (displaystyle F_text{Арх}=33,75text{ Н}?) (Ответ дайте в сантиметрах.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV,] где (displaystyle rho_text{в}) – плотность жидкости, в которую погружен кубик, (displaystyle V) – объем погруженной части тела. Так как куб погружен целиком, то (displaystyle V=a^3), получим: [F_text{Арх}=rho_text{в} ga^3] Выразив из этой формулы сторону (displaystyle a), получаем [a=sqrt[3]{frac{F_text{Арх}}{rho_text{в}g }}] Подставив значения в формулу, получим: [a=sqrt[3]{frac{33,75text{ Н}}{10text{ м}/{c^2}cdot1000text{ кг}/text{м}^3}}=0,15text{ м}=15text{ cм }]
Ответ: 15
Однородный цилиндр, изготовленный из материала плотностью (displaystyle rho=600) кг/м(^3), с радиусом основания (displaystyle R=25) см и высотой (displaystyle H=20) см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)

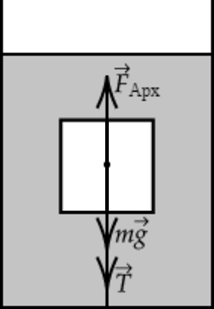
Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: [vec T+vec F_text{Арх}+mvec g=mvec a,] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [T- F_text{Арх}+mg=0, quad(1)] массу цилиндра можно рассчитать, исходя из формулы (displaystyle rho=frac {m}{V} Rightarrow m=rho V,) где V – объем цилиндра, который можно вычислить по формуле [V=pi R^2 H] Из формулы (1) выразим силу натяжения нити T:[T=F_text{Арх}-mg=rho_text{в}gV-rho gV=Vg(rho_text{в}-rho)=pi R^2 Hg(rho_text{в}-rho),] где (displaystyle rho_text{в}) – плотность воды, подставим в получившееся выражение численные значения:[T=3,14cdot0,25^2text{ м}cdot0,2text{ м}cdot 10text{ м}/text{с}^2 cdot (1000text{ кг}/text{м}^3-600text{ кг}/text{м}^3)=157text{ Н }]
Ответ: 157
Однородный кубический предмет с ребром (displaystyle a=18) см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна (displaystyle rho_text{др}=340) кг/м(^3), плотность эфира (displaystyle rho_text{э}=720) кг/м(^3). (Ответ дайте в сантиметрах.)
Запишем условие равновесия кубика на поверхности эфира: [F_text{ Арх}=mg, quad(1)] где (F_text{ Арх}) – выталкивающая сила, действующая на брусок, (displaystyle m) – масса кубика, которую можно рассчитать, исходя из формулы (displaystyle rho_text{др}=frac {m}{V} Rightarrow m=rho_text{др} V,) где V – объем кубика, который можно вычислить по формуле [V=a^3.] Выталкивающая сила равна: [F_text{ Арх}=rho_text{э}gV_text{пчт},] где (displaystyle V_text{пчт}) – объем погруженной части кубика,[V_text{пчт}=xa^2,] где (displaystyle x) – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: [rho_text{э}gxa^2=rho_text{др}a^3] [rho_text{э}x=rho_text{др}a, text{ выразим } x=frac{rho_text{др}a}{rho_text{э}}.] Пусть (displaystyle y) – длина части стороны, находящейся над эфиром, можем записать: [y=a-x,] искомая разница длин (displaystyle delta=y-x=a-2x=a-2cdot dfrac{rho_text{др}a}{rho_text{э}}=a(1-2cdot dfrac{rho_text{др}}{rho_text{э}})) подставим в получившееся выражение численные значения: [displaystyle delta=0,18text{ м}(1-2cdot dfrac{340text{ кг}/text{м}^3}{720text{ кг}/text{м}^3})=0,01text{ м}=1text{ см}]
Ответ: 1
В некий резервуар было налито 1000 литров жидкости плотностью (displaystyle rho_1=1500) кг/м(^3). В этой жидкости в равновесии плавает кубик, погруженный в воду на (displaystyle x=130) см. Длина стороны кубика равна (displaystyle a=200) см. В сосуд доливают ещё 1000 литров жидкости плотностью (displaystyle rho_2=1100) кг/м(^3) и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)
В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. [rho_text{нов}=dfrac{rho_1+rho_2}{2}] Так как кубик плавает на поверхности, то можно записать: [mg=F_text{Арх},] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна:[F_text{Арх1}=rho_1 g V_text{пчт1},] где (displaystyle V_text{пчт1}=a^2x) – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: [F_text{Арх2}=rho_text{нов} g V_text{пчт2}=dfrac{rho_1+rho_2}{2}g V_text{пчт2},]где (displaystyle V_text{пчт2}=a^2y) – объем погруженной части куба до смешивания, (displaystyle y) – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим [rho_1 g a^2x=dfrac{rho_1+rho_2}{2} g a^2y] [rho_1x=dfrac{rho_1+rho_2}{2}y,] выразим отсюда y: [y=frac{2rho_1 x}{rho_1+rho_2},] подставим в получившееся выражение численные значения: [y=frac{2cdot1500text{ кг}/text{м}^3 cdot1,3text{ м}}{1500text{ кг}/text{м}^3+1100text{ кг}/text{м}^3}=1,5text{ м}]
Ответ: 1,5
Стеклянный шарик опускается в воде с ускорением (displaystyle a=6) м/с(^2). Найти плотность стекла. Плотность воды (displaystyle rho_text{в}=1000) кг/м(^3). Силами вязкого трения пренебречь. (Ответ дайте в кг/м(^3).)
При движении шарика в воде на него действует сила тяжести (displaystyle mvec g) и сила Архимеда (displaystyle F_text{Арх}). Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: [vec F_text{Арх}+mvec g=mvec a,] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [mg- F_text{Арх}=ma,] Отсюда с учетом выражения для силы Архимеда (displaystyle F_text{Арх}=rho_text{в} g V), где V – объем шарика, а
(displaystyle rho_text{в}) – плотность воды, получим: [mg- rho_text{в} g V=ma,] Выразим массу шарика:[m=frac{rho_text{в} g V}{g-a}.] Исходя из формулы, плотность стекла равна [displaystyle rho_text{ст}=frac {m}{V}=frac{rho_text{в} g V}{(g-a)V}=frac{rho_text{в} g }{g-a},] подставим в получившееся выражение численные значения: [rho_text{ст}=frac{1000 text{ кг}/text{м}^3cdot 10text{ м}/text{с}^2 }{10text{ м}/text{с}^2-6text{ м}/text{с}^2}=2500text{ кг}/text{м}^3]
Ответ: 2500
Однородный шарик, изготовленный из материала плотностью (displaystyle rho=2000) кг/м(^3) погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
(displaystyle F_text{Арх}=100) Н? (Ответ дайте в сантиметрах и округлите до целых.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV_text{пчт},] где (displaystyle rho_text{в}) – плотность воды, (displaystyle V_text{пчт}) – объем погруженной части тела. Так как шар полностью опущен в воду, то [V_text{пчт}=frac43pi R^3,] где (displaystyle R) – радиус шара, получим: [F_text{Арх}=rho_text{в} gfrac43pi R^3, (1)] выразим из формулы R: [R=sqrt[3]{frac{3F_text{Арх}}{4rho_text{в}gpi}}] Подставив значения в формулу, получим: [R=sqrt[3]{frac{3 cdot100text{ Н}} {4 cdot1000 text{ кг}/text{м}^3cdot10text{ м}/{c^2}cdot3,14}} approx0,13text{ м}=13text{ см }]
Ответ: 13
Источник
