Сосуд разделен адиабатной перегородкой
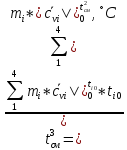
МГТУ им. Н. Э. Баумана
Домашнее задание №1
по термодинамике:
«Газовые смеси»
Вариант №15
Студент: Романов А.С.
Группа: Э7-52
Преподаватель: Чирков А.Ю.
-2012-
Условие задания:
Сосуд разделен адиабатной перегородкой на четыре части, в каждой из которых содержатся различные газы. После того как перегородка убрана, происходит «смешение в объеме» без теплообмена с окружающей средой. Состояния газов до смешения характеризуются следующими параметрами: массой mi0, кг; объемом Vi0, м3; температурой ti0, ˚С.
Необходимо определить:
температуру смеси после завершения процесса смешения t;
давление смеси Р, МПа;
газовую постоянную R, Дж/(кг*К);
среднюю молярную массу смеси µ, кг/моль;
объемный состав смеси {ri};
молярный состав смеси {ni};
парциальное давление компонентов смеси {pi}, МПа;
приведенные объемы компонентов смеси {Vi}, МПа;
истинную молярную теплоемкость смеси при р=const для температуры смеси, которая устанавливается после окончания процессов смешения ср ,Дж/(кмоль*К);
истинную объемную теплоемкость смеси при р=const после окончания процесса смешения C , Дж/(м *К);
истинную массовую теплоемкость смеси при р=const после окончания процесса смешения с, Дж/(кг*К);
количество теплоты Q (Дж), которое необходимо отвести от 3 кмоль смеси для охлаждения их при р=const до температуры смеси 300 К;
количество теплоты Q (Дж), которое необходимо отвести от 4 м смеси для охлаждения их при р=const до температуры смеси 300 К;
количество теплоты Q (Дж), которое необходимо отвести от 5 кг смеси для охлаждения их при р=const до температуры смеси 300 К.
Исходные данные:
Газ | mi0, кг | Vi0, м3 | ti0, ˚С |
O2 | 13 | 2,1 | 160 |
N2 | 16 | 1,6 | 260 |
H2 | 11 | 3,1 | 860 |
CO | 6 | 3,6 | 1060 |
Молярные массы газов:
; ; ;
Решение:
При получении значений из таблицы используется линейная интерполяция:
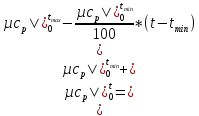 (1.1)
(1.1)
Температура смеси после завершения процесса смешения.
Нулевое приближение:
Первое приближение:
(1.2)
Вычислим теплоемкости, входящие формулу (1.2), необходимые для расчета суммарной внутренней энергии газов до смешения, а также температуры смеси в первом приближении:
O2:
СО2:
SO2:
H2O:
Подставим полученные значения:
кДж – суммарная внутренняя энергия газов до смешения (остаётся постоянной для всех последующих приближений).
Второе приближение:
(1.3)
Вычислим теплоемкости, входящие формулу (1.3):
O2:
СО2
SO2:
H2O:
Подставим полученные значения:
Третье приближение:
(1.3)
Вычислим теплоемкости, входящие формулу (1.3):
O2:
СО2
SO2:
H2O:
Подставим полученные значения:
Принимаем:
Давление смеси , МПа.
Для определения давления используем формулу:
где
– масса смеси;
– объем смеси;
– газовая постоянная смеси (см. пункт 3).
Тогда:
Постоянная газовая смеси .
где – массовая доля i-го газа.
Тогда:
,
Средняя молярная масса смеси – .
Состав смеси в объемных долях –
При одинаковых температуре и давлении всех газов одинаково, поэтому:
(см. пункт 6)
O2:
СО2:
SO2:
H2O:
Состав смеси в молярных долях – .
O2:
СО2:
SO2:
H2O:
Проверка: , верно.
Парциальные давления компонентов смеси – .
O2:
СО2:
SO2:
H2O:
Парциальные объемы компонентов смеси – .
O2:
СО2:
SO2:
H2O:
Истинная молярная теплоемкость смеси при , установившеюся после смешения .
O2:
СО2
SO2:
H2O:
Истинная объемная теплоемкость смеси при , установившеюся после смешения .
.
Истинная массовая теплоемкость смеси при , установившеюся после смешения .
.
Количество теплоты, которое необходимо отвести от 3 кмоль смеси для ее охлаждения при от температуры смеси до температуры .
Определим среднюю молярную теплоемкость смеси при процессе:
O2:
СО2
SO2:
H2O:
.
Кол-во теплоты, которое необходимо отвести от 4 м3 (н. у.) смеси для ее охлаждения при от температуры смеси до температуры
.
Определим среднюю объемную теплоемкость смеси при процессе:
.
.
Кол-во теплоты, которое необходимо отвести от 5кг смеси для ее охлаждения при от температуры смеси до температуры .
Определим среднюю массовую теплоемкость смеси при процессе:
Знак минус указывает на то, что теплота отводится от смеси.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Сосуд, теплоизолированный от окружающей среды, разделен адиабатными перегородками на четыре объема, в каждом из которых содержится определенный газ. После того как перегородки убраны, происходит смешение в постоянном объеме, равным сумме объемов четырех частей с разными газами. Состояние газов до смешения характеризуются параметрами: массой 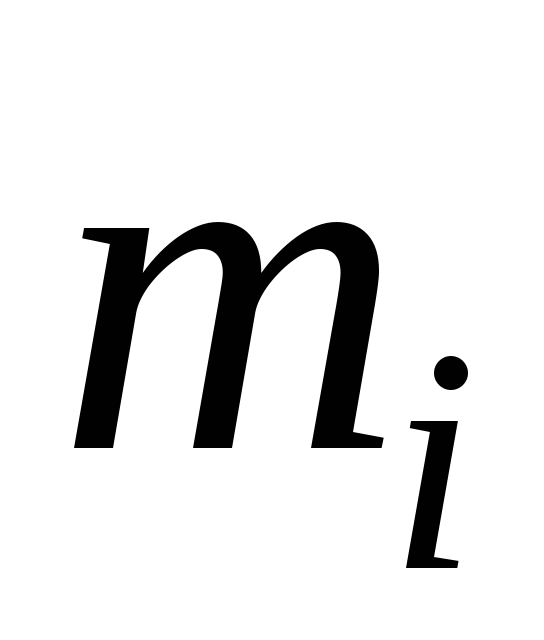 , кг, объемом
, кг, объемом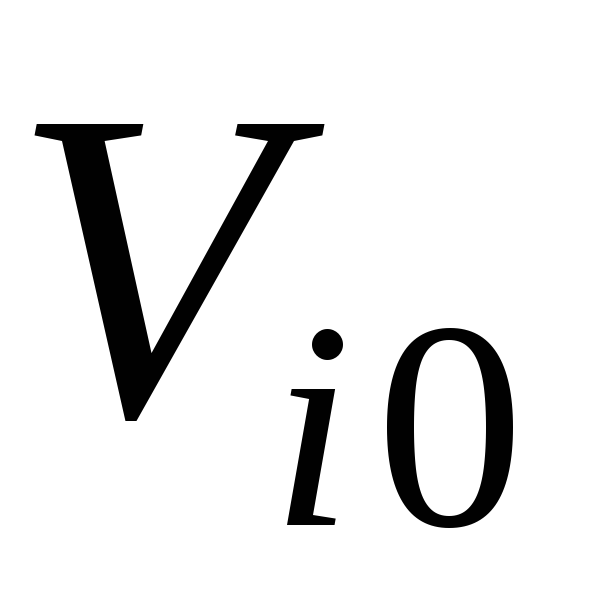 , м3; температурой
, м3; температурой 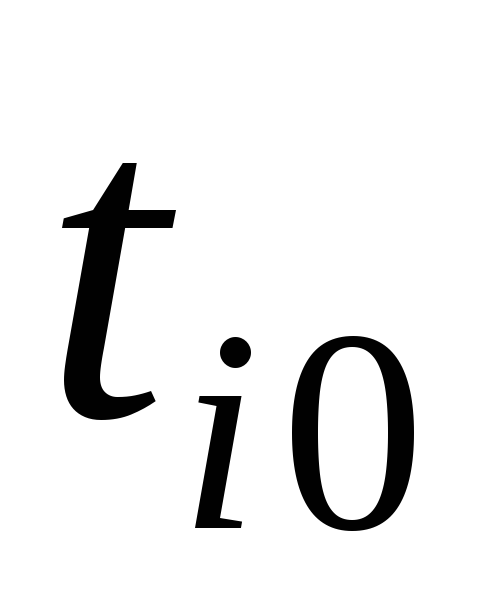 ,°С, где (
,°С, где (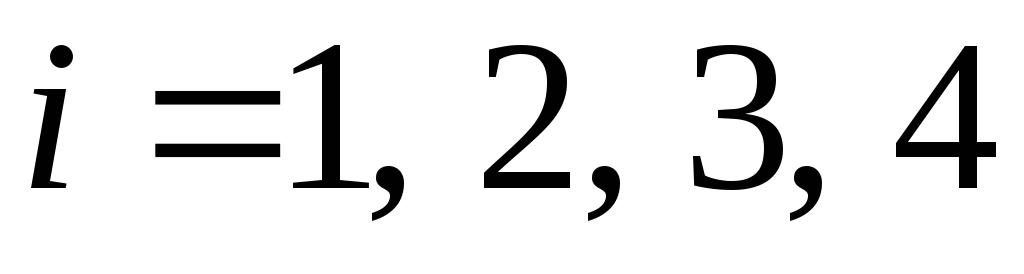 ). Данные для расчета необходимо брать в табл. 2 Приложения 1 в соответствии с заданным номером варианта.
). Данные для расчета необходимо брать в табл. 2 Приложения 1 в соответствии с заданным номером варианта.
В процессе работы над индивидуальным домашнем заданием необходимо определить:
– температуру смеси после завершения процесса смешения –  ,°С;
,°С;
– давление газовой смеси – 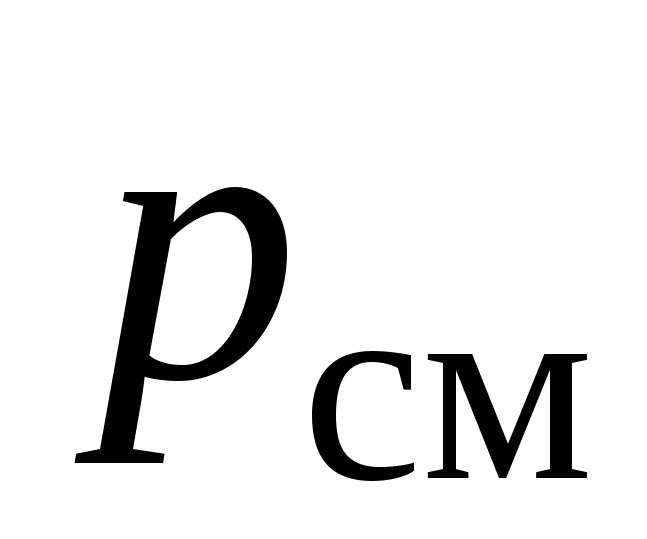 , МПа;
, МПа;
– газовую постоянную газовой смеси, кДж/(кг·К);
– кажущуюся молярную массу смеси – 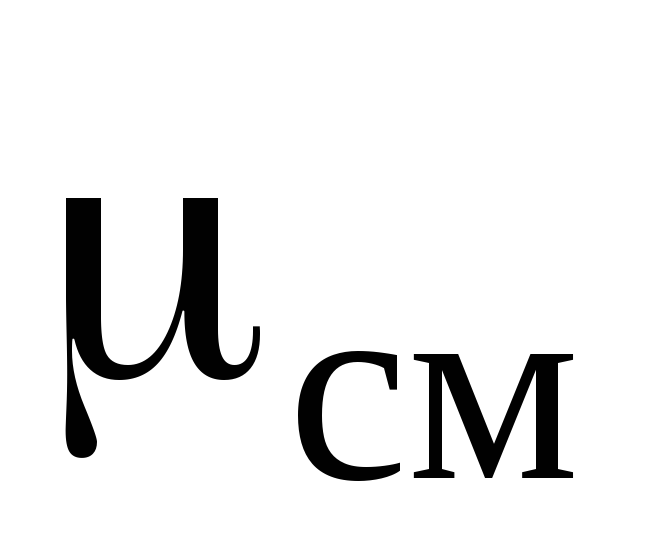 , кг/моль;
, кг/моль;
– состав газовой смеси в массовых долях;
– парциальные давления компонентов смеси – 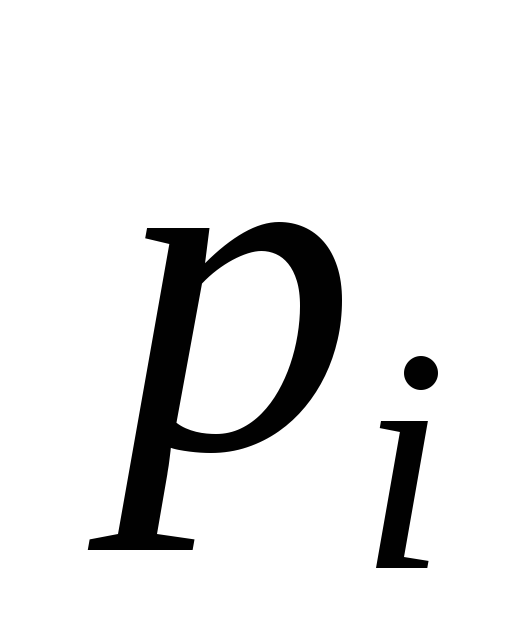 , МПа;
, МПа;
– истинную мольную теплоемкость смеси при 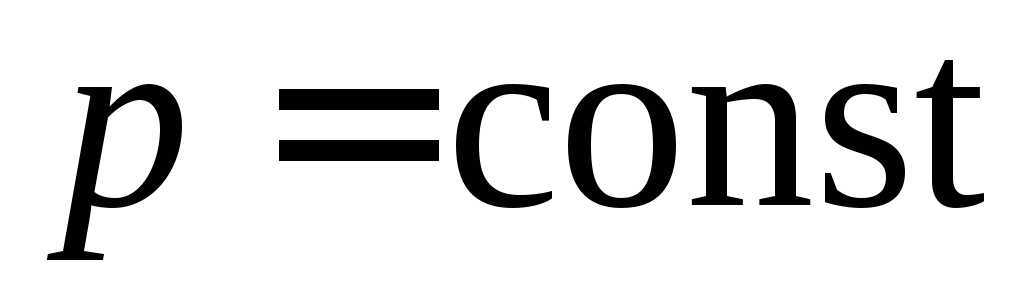 для температуры установившейся после смешения
для температуры установившейся после смешения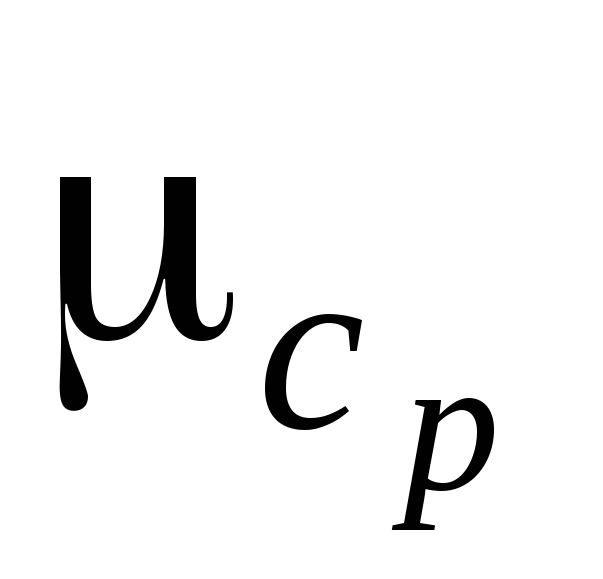 , кДж/(кг·К);
, кДж/(кг·К);
– найти приращение энтропии системы в процессе необратимого смешения, кДж/К;
– рассчитать эксергию компонентов, газовой смеси и потери эксергии в процессе смешения: 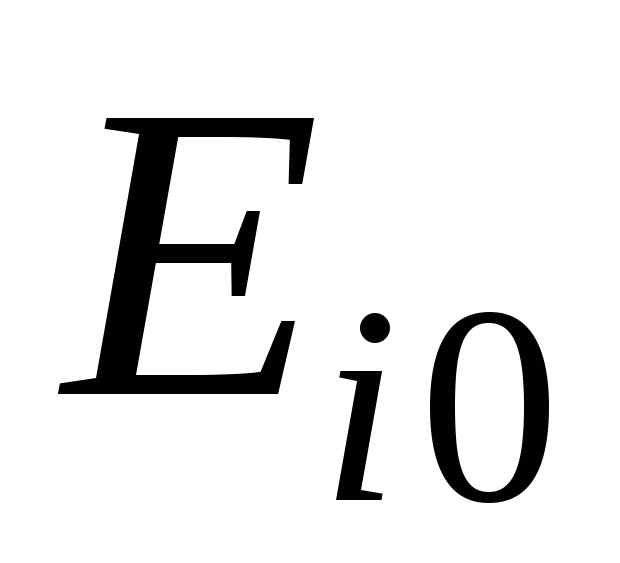 ,
, ,
,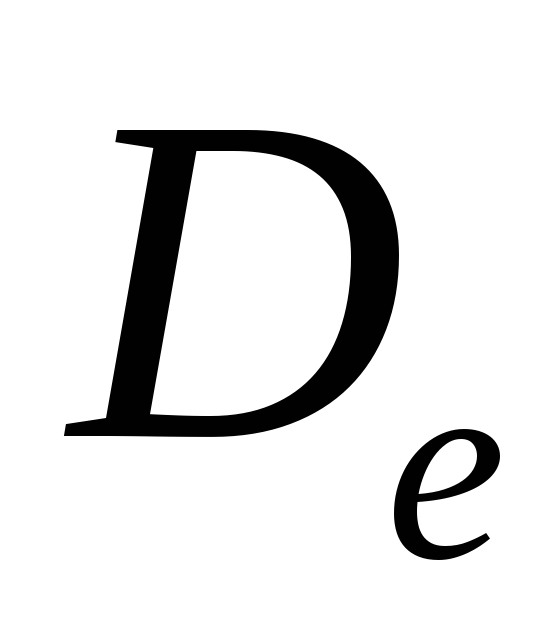 , кДж/К;
, кДж/К;
– построить эксергетическую диаграмму процесса смешения в постоянном объеме.
При выполнении расчета процесса смешения счить компоненты смеси идеальными газами. При определении истинной и средней теплоемкостей, данные брать по табл. 1-5 Приложения 2. При вычислении воспользоваться линейной интерполяцией.
Температуру смеси после окончания процесса смешения найти графически или методом последовательных приближений. При этом начальное приближение для температуры смеси можно вычислить, пологая теплоемкости компонентов смеси равными, по следующей зависимости:
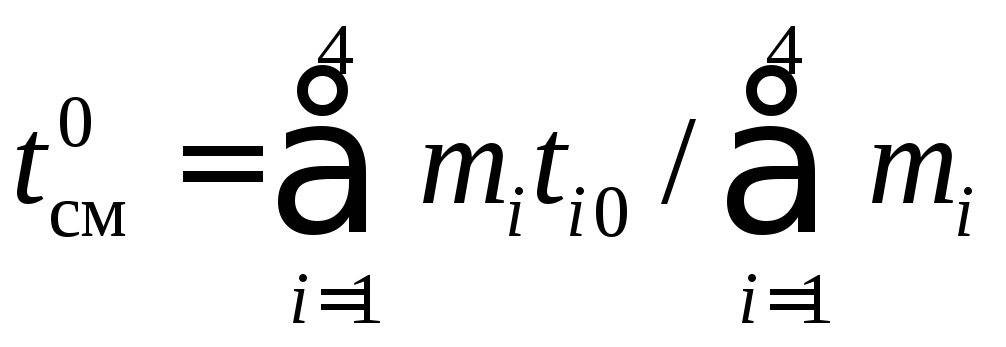 .
.
Точность вычисления температуры смеси должна быть не менее 1 К. В расчетах использовать систему СИ единиц.
2.3. Пример выполнения расчета
Сосуд разделен перегородкой на две части, объемы которых
V1 = 1,5 м3 и V2 = 1 м3. В первой части содержится азот массой m1 = 10 кг при температуре t1 = 120 °C; в другой части – гелий массой m2 = 5 кг при
t2 = 860 °C. Найти давление, температуру и энтропию смеси после того, как перегородка будет убрана и процесс смешения закончится.
Решение.
Воспользуемся законом сохранения энергии (2.1) и запишем:
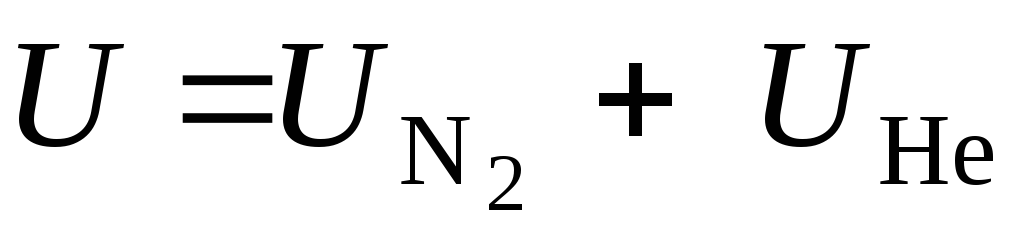
или через удельные энтальпии с учетом выклада каждого из компонентов
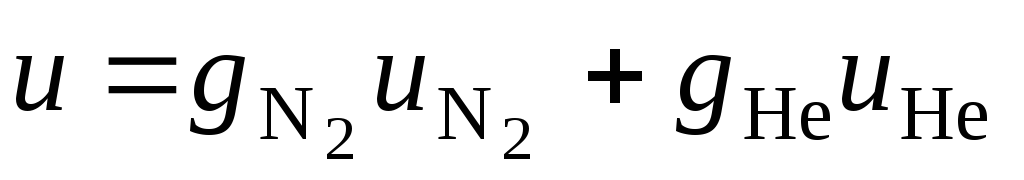 ,
,
где массовые доли азота и гелия найдем из выражения
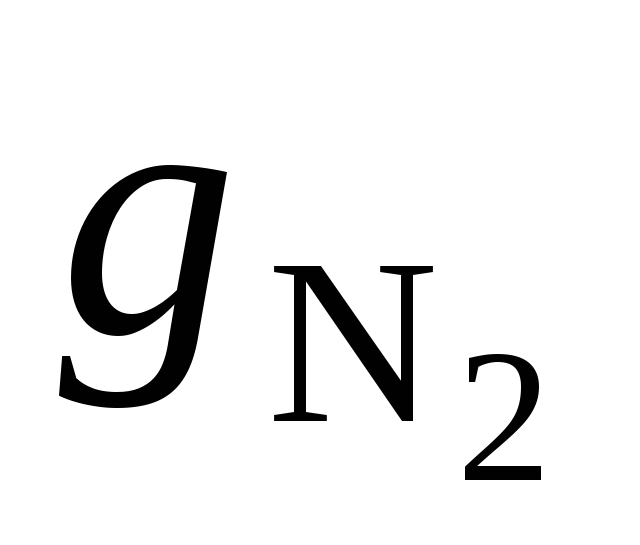 =
= 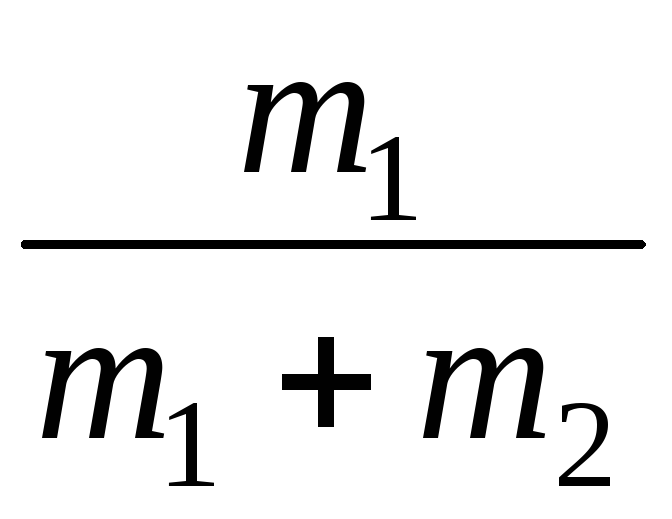 ;gHe =
;gHe = 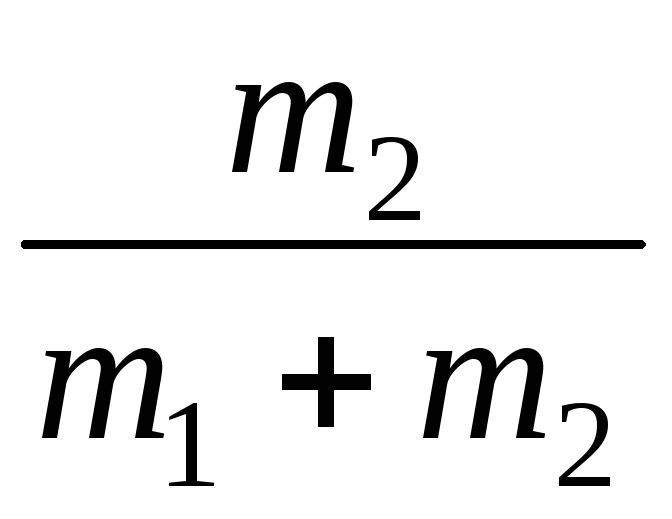 .
.
Удельную внутреннюю энергию азота находим по табл. 1 Приложения 2, а удельную внутреннюю энергию гелия uHe воспользовавшись положениями молекулярно-кинетической теории. Гелий – одноатомный газ, у которого, имеются три степени свободы. Тогда выражение для удельной внутренней энергии может быть записано в виде
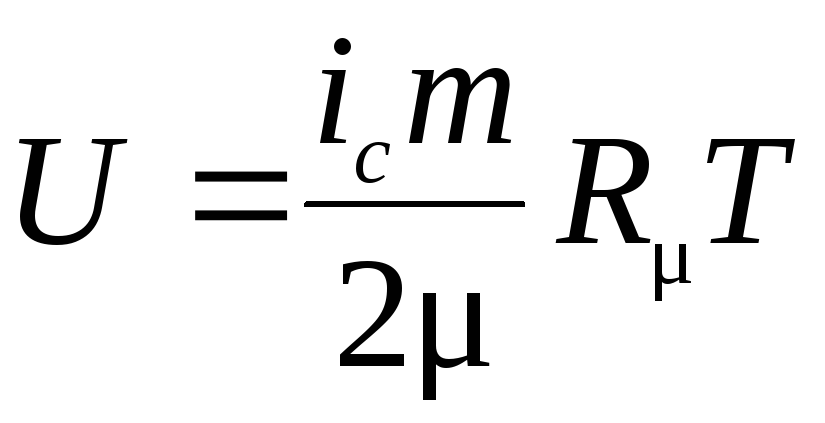 ;
; 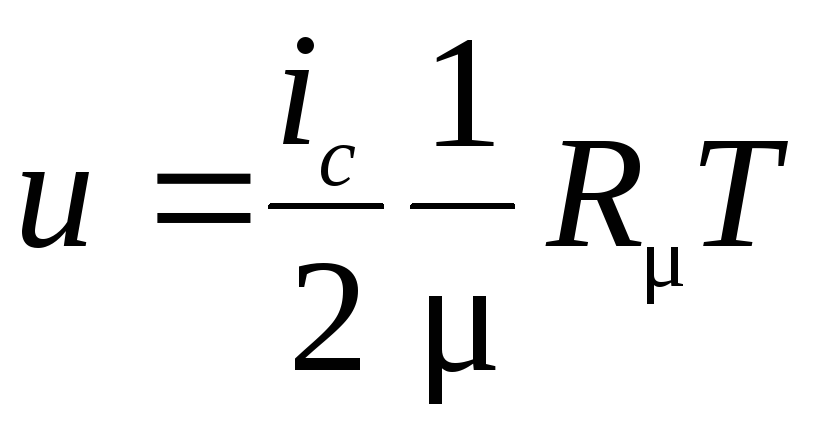
или после подстановки численных значений величин, входящих в зависимость
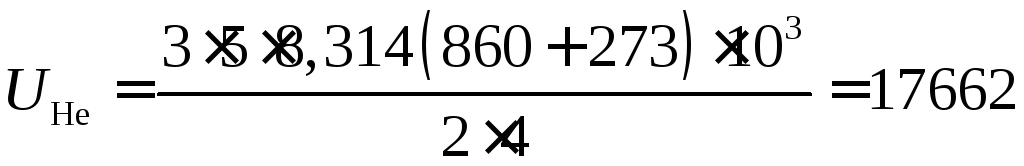 кДж;
кДж;
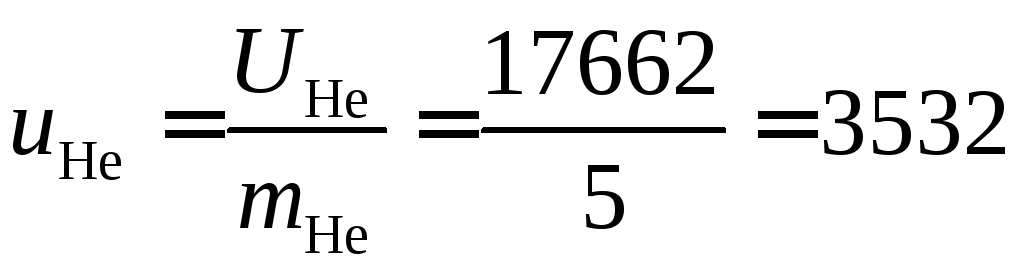 кДж/кг.
кДж/кг.
Удельная внутренняя энергия азота из таблиц 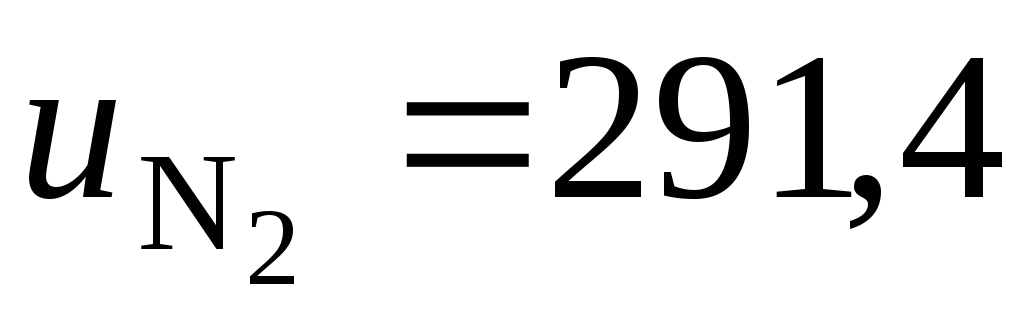 кДж/кг
кДж/кг
или если рассчитать по изложенной методике
 кДж;
кДж;
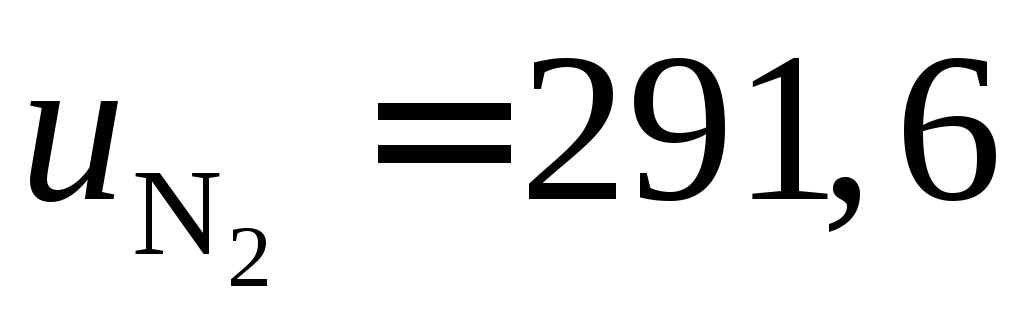 кДж/кг.
кДж/кг.
Рассчитаем удельную внутреннюю энергию заданной смеси азота и аргона:
 кДж/кг.
кДж/кг.
Для определения средней температуры, используя отмеченную методику, рассчитаем внутреннюю энергию смеси при температурах, находящихся в области предполагаемого численного значения искомой величины. Результаты внесем в табл. 2.1.
По полученным данным, пользуясь интерполяцией или графиком t= f(u), построенным с использованием результатов расчета находим температуру газовой смеси.
По графику  (рис. 2.3) находим, что температура смеси составляет ~611°С.
(рис. 2.3) находим, что температура смеси составляет ~611°С.
t, °C | T, К |
| uHe= | gN2 uN2, кДж/кг | gHeuHe, кДж/кг | u = = кДж/кг |
400 500 600 700 800 | 500 571 648 722 796 | 2098 2412 2724 3036 3348 | 333 383 432 481 531 | 699 804 908 1012 1016 | 1032 1187 1340 1493 1647 |
Таблица 2.1
Воспользуемся уравнением состояния Клапейрона-Менделеева и найдем парциальные давления компонентов смеси
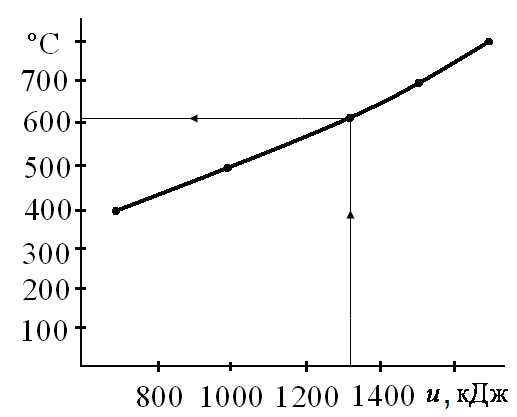
Рис. 2.3. Зависимость температуры смеси от ее удельной внутренней энергии
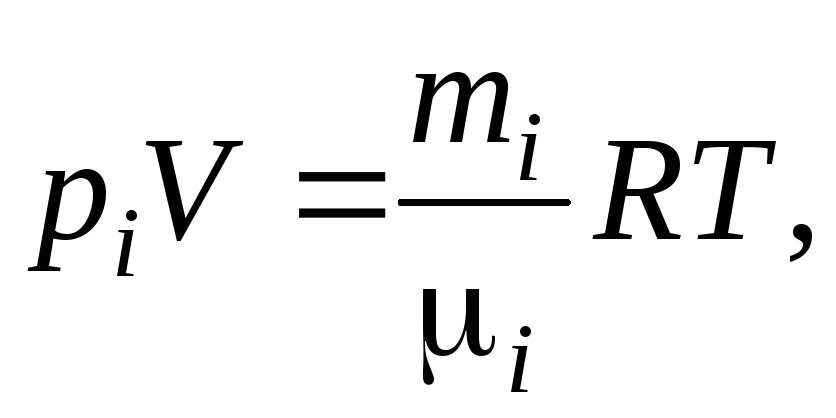
где V – объем газовой смеси 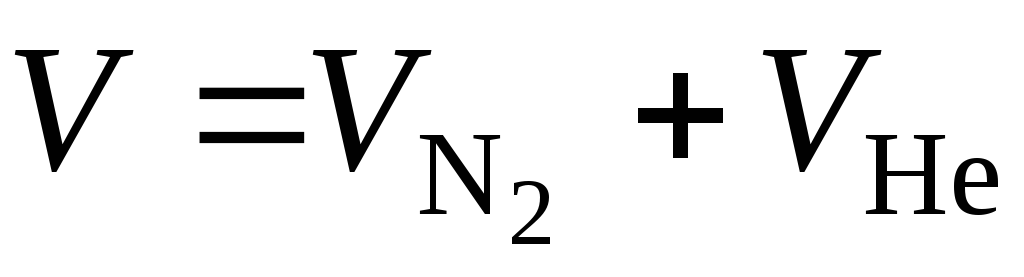 .
.
Парциальное давление азота:
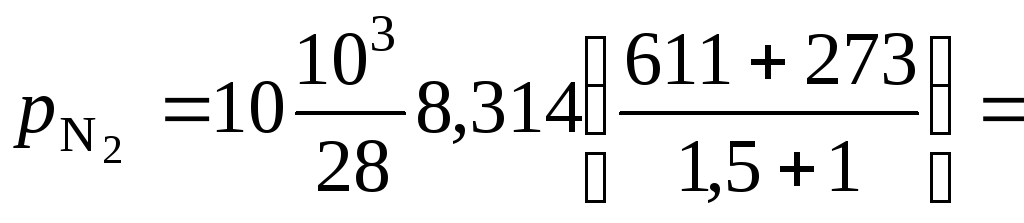
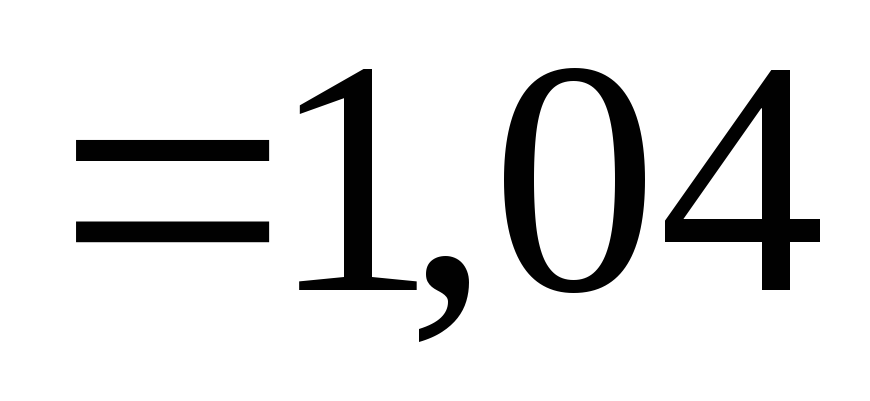 МПа.
МПа.
Парциальное давление гелия:
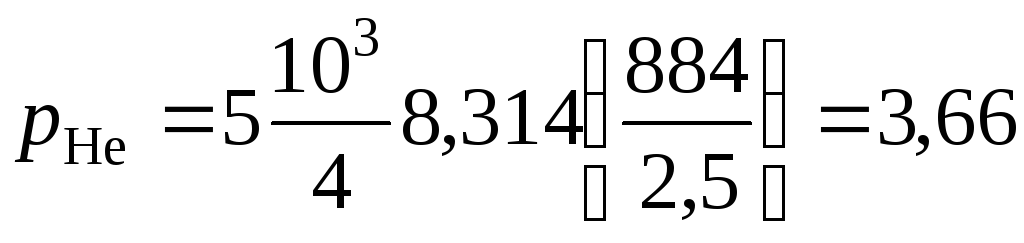 МПа.
МПа.
Давление газовой смеси в соответствии с законом Дальтона найдем как сумму парциальных давлений
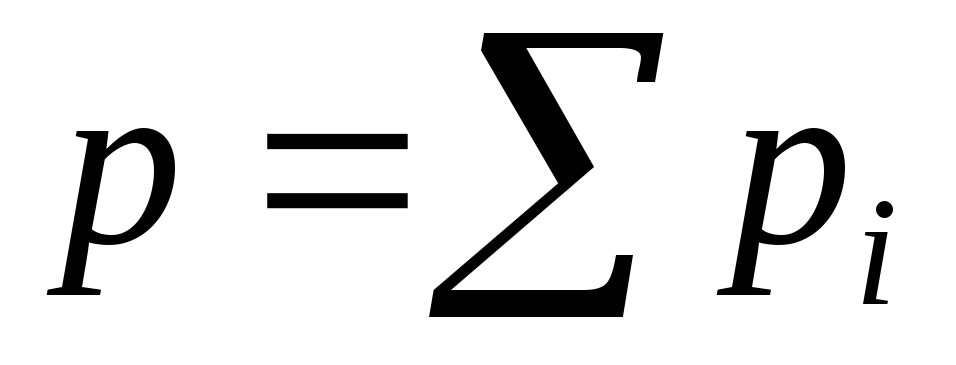 или
или 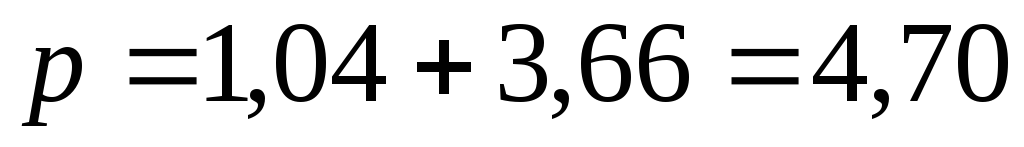 МПа.
МПа.
Массовые доли компонентов
;
;
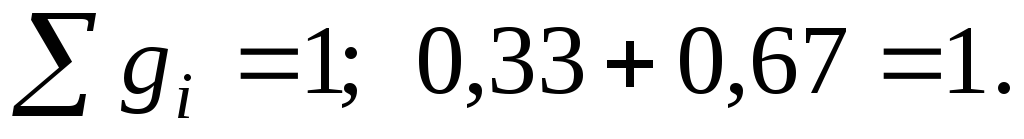
Газовая постоянная смеси
Кажущая молярная масса газовой смеси
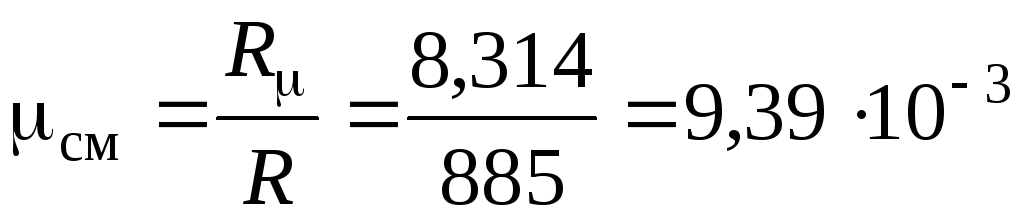 кг/моль.
кг/моль.
Объемные доли компонентов
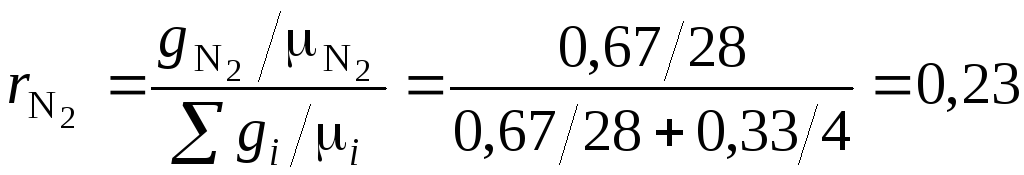 ;
;
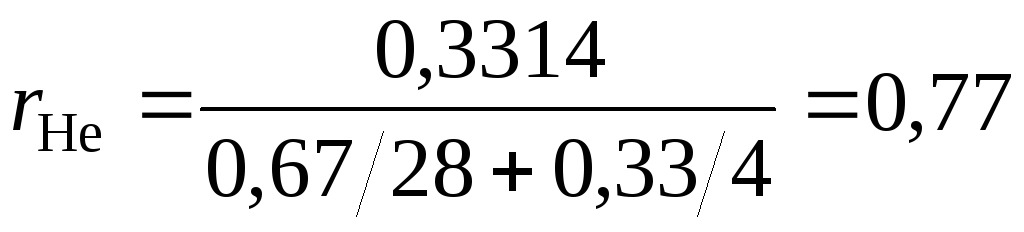 .
.
Рассчитаем давление смеси
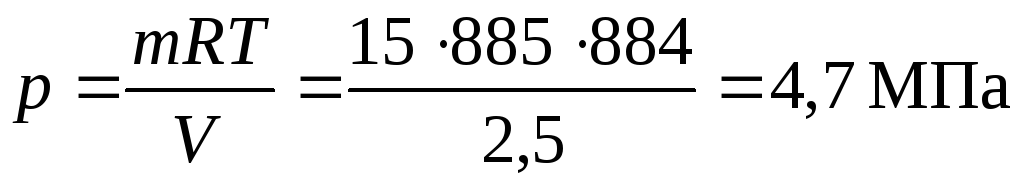 .
.
Парциальные давления компонентов
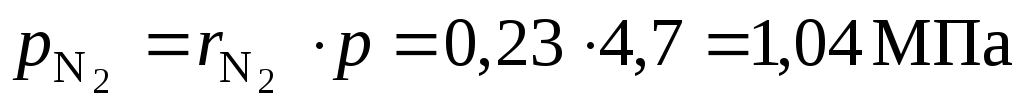 ;
;
Давление смеси
Рассчитывая энтропию смеси сделаем предположение о том, что при  МПа и
МПа и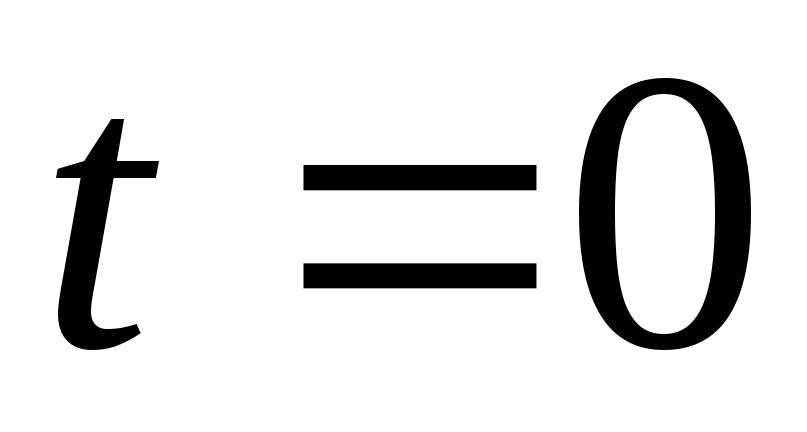 °С, т. е. при нормальных физических условиях, энтропия газов (
°С, т. е. при нормальных физических условиях, энтропия газов (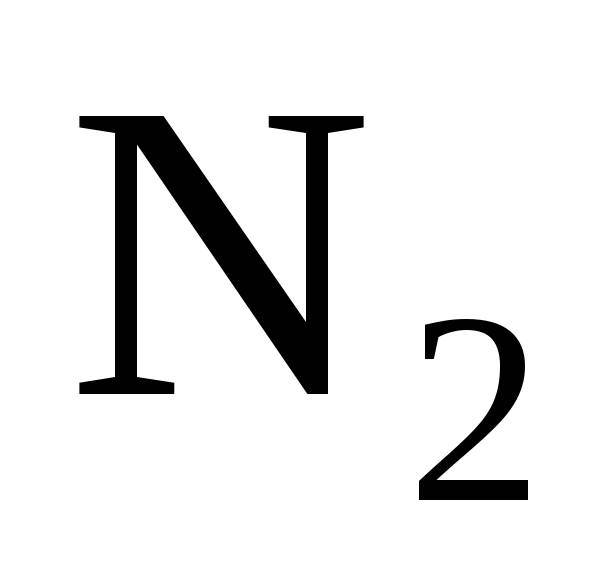 и
и ) равна нулю. Такое допущение правомочно, т. к. нас интересует не абсолютная величина энтропии, а ее отклонение от некоторого уровня, выбранного в осуществляемом расчете за нулевой. Энтропия газов до смешения равна сумме энтропии 10 кг азота и 5 кг гелия. Для их определения по известным начальным состояниям азота и гелия выпишем из таблиц Приложения 2 необходимые при расчете значения теплоемкостей.
) равна нулю. Такое допущение правомочно, т. к. нас интересует не абсолютная величина энтропии, а ее отклонение от некоторого уровня, выбранного в осуществляемом расчете за нулевой. Энтропия газов до смешения равна сумме энтропии 10 кг азота и 5 кг гелия. Для их определения по известным начальным состояниям азота и гелия выпишем из таблиц Приложения 2 необходимые при расчете значения теплоемкостей.
Найдем давления компонентов до смешения, воспользовавшись уравнением Клапейрона-Менделеева
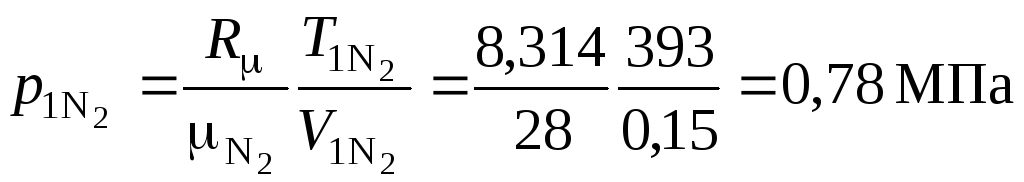 ;
;
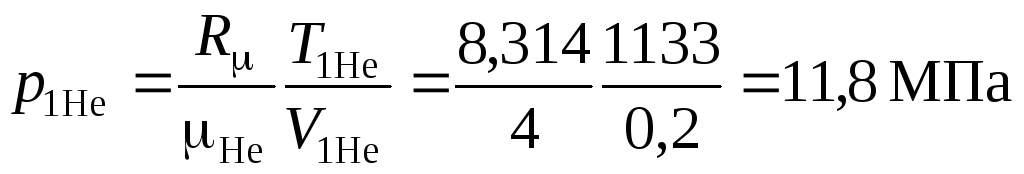 .
.
Теплоемкости компонентов из табл. Приложения 2:
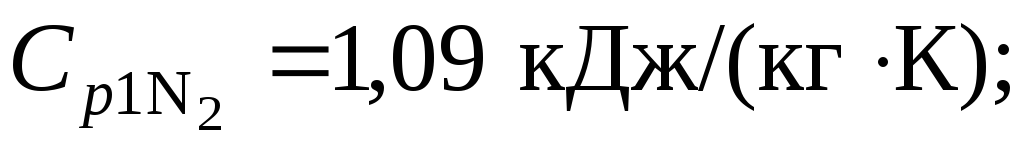
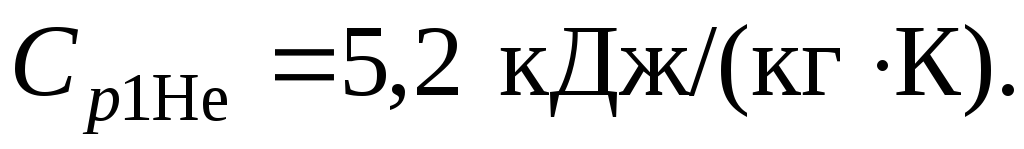
Удельная энтропия азота в начальном состоянии
Удельная энтропия гелия до смешения
Энтропия системы азот гелий до смешения равна сумме энтропий подсистем в соответствии с аддитивностью энтропии
 ;
;
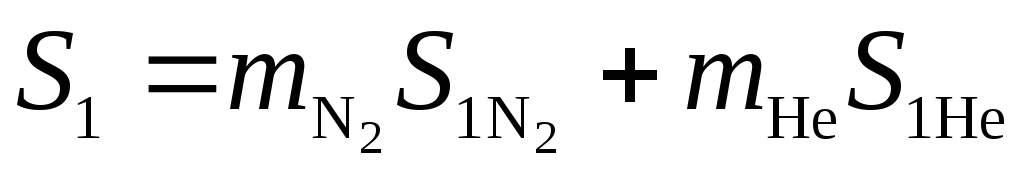 ;
;
Рассчитаем энтропию газовой смеси
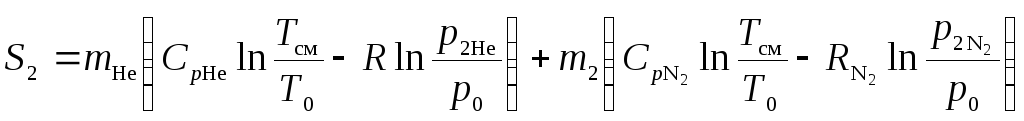 .
.
Подставим численные значения
В расчете не учитывалась зависимость теплоемкости от температуры.
Рассчитаем приращение энтропии за счет необратимости процесса смешения

Потери эксергии в процессе смешения найдем, воспользовавшись уравнением Гюи-Стодолы:
Эксергия термодинамической системы из 10 кг азота и 5 кг гелия до смешения
.
Энтропию компонентов при параметрах окружающей среды, как было ранее отмечено, будем считать равной нулю. Тогда для начального состояния гелия и азота рассчитаем численные значения внутренней энергии и удельных объемов. Предполагая газы идеальными, воспользуемся зависимостью внутренней энергии от температуры и удельной изохорной теплоемкости
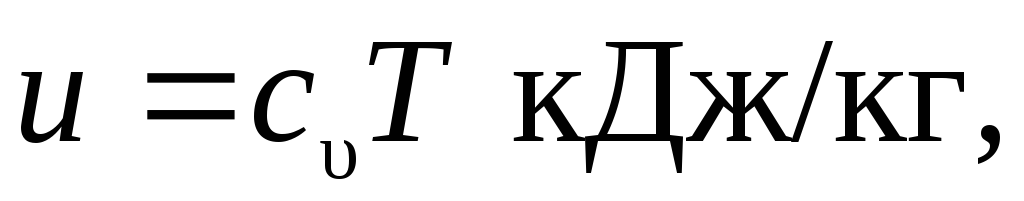
где массовая теплоемкость может быть выражена через мольную теплоемкость и молярную массу газа  .
.
Мольная теплоемкость газа с использованием молекулярно кинетических основ в рамках классической термодинамики равна:
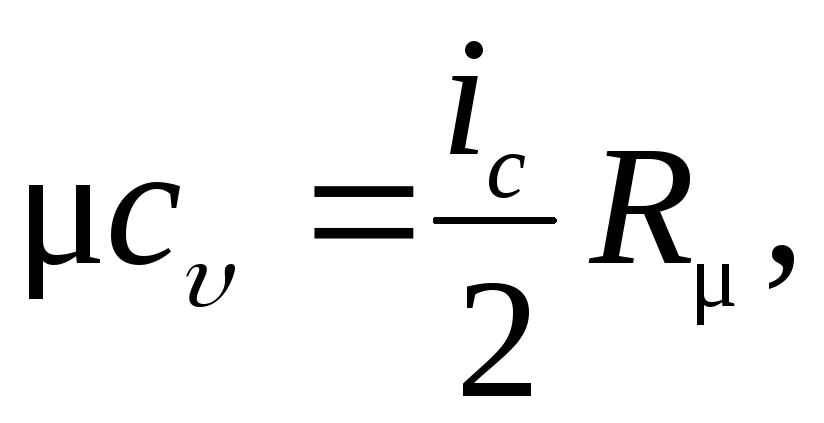
где iс – число степеней свободы молекулы газа.
Для гелия как одноатомного газа 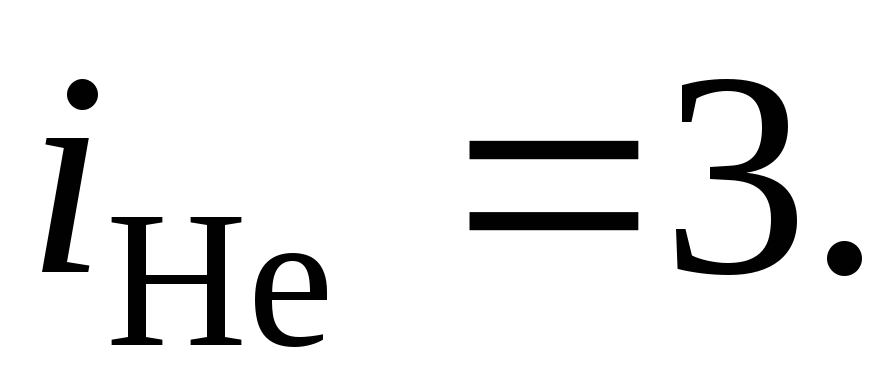
Для двухатомного азота 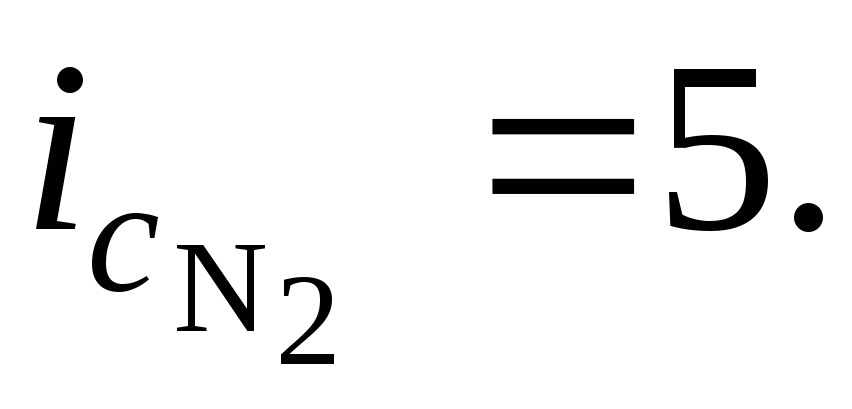
Тогда удельная внутренняя энергия гелия равна:
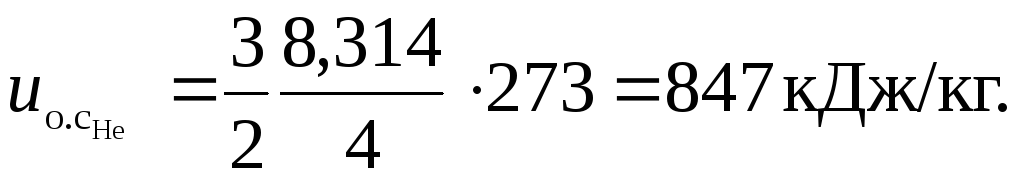
Для азота
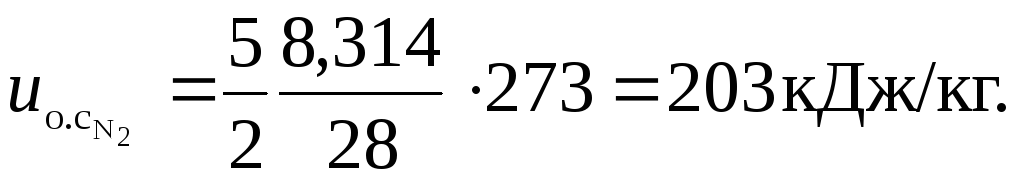
Удельные объемы компонентов до смешения найдем, воспользовавшись исходными данными
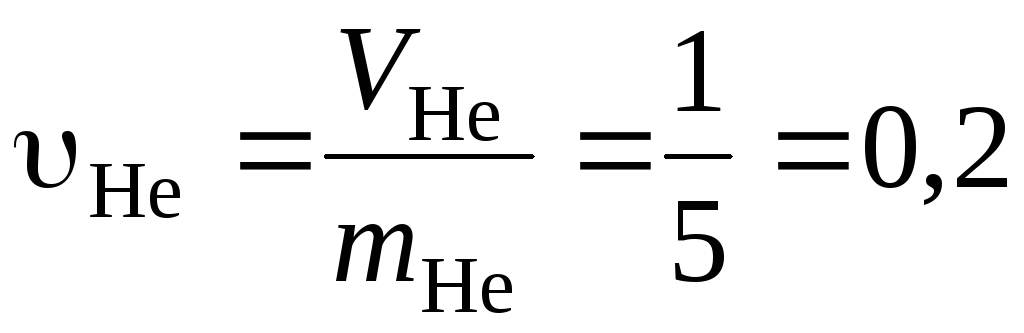 м3/кг;
м3/кг;
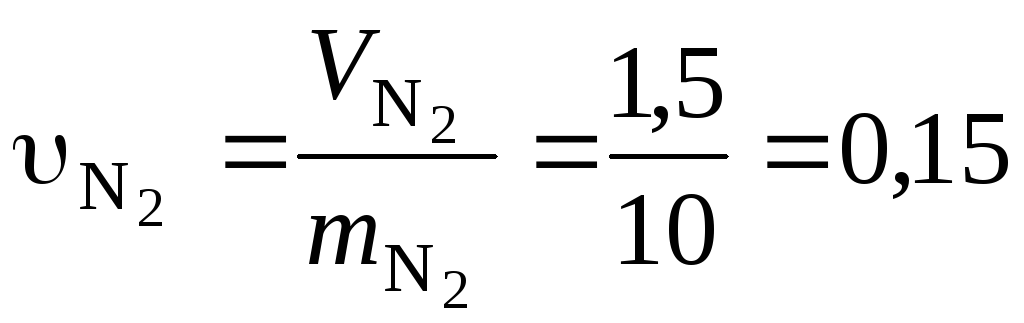 м3/кг.
м3/кг.
Удельные объемы компонентов при нормальных условиях найдем, воспользовавшись уравнением Клапейрона-Менделеева
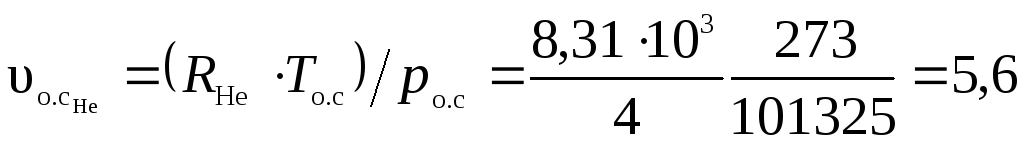 м3/кг;
м3/кг;
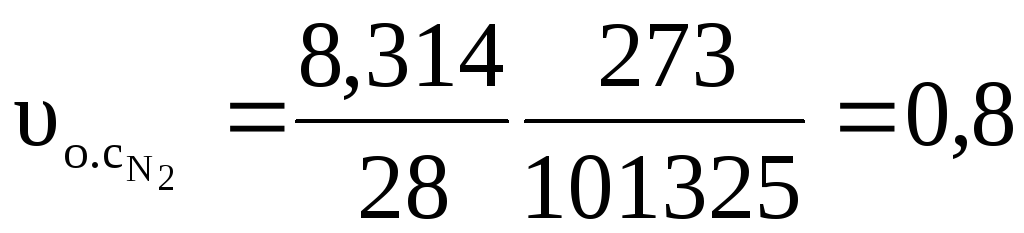 м3/кг.
м3/кг.
Рассчитаем суммарную эксергию азота и гелия до процесса смешения
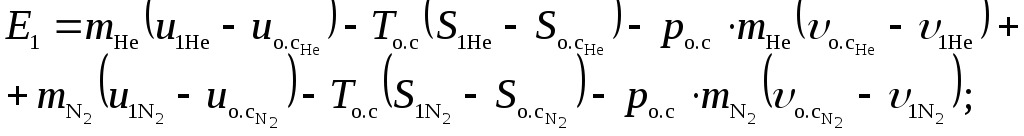
Подставим численные значения
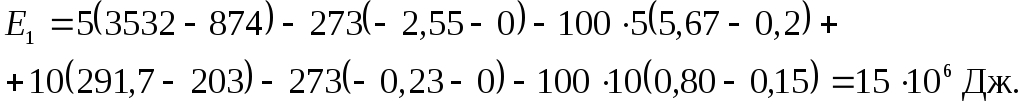
Удельные внутренние энергии гелия 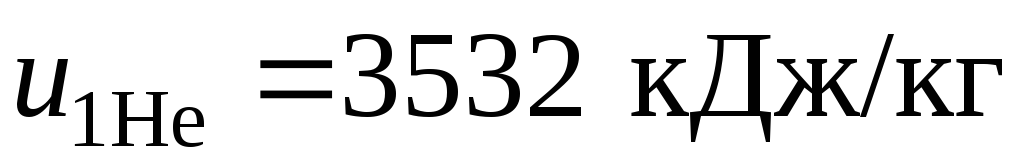 и
и
азота  взяты из таблиц Приложения 2.
взяты из таблиц Приложения 2.
Определим эксергию образовавшейся газовой смеси
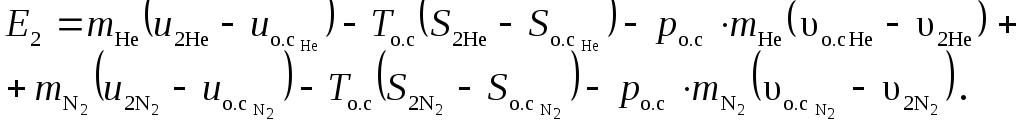
Из таблиц Приложения 2 найдем удельную внутреннюю энергию гелия и азота в состоянии соответствующим газовой смеси.
 ;
; 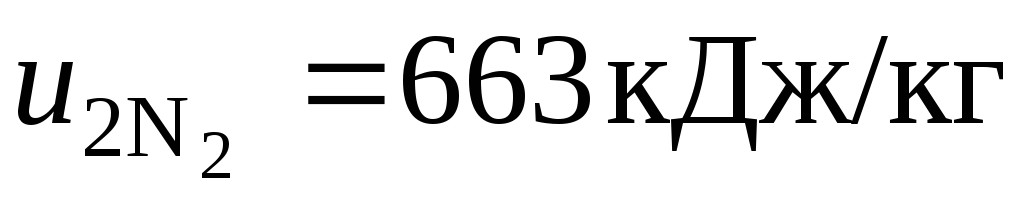 .
.
После подстановки рассчитаем численное значение эксергии газовой смеси:
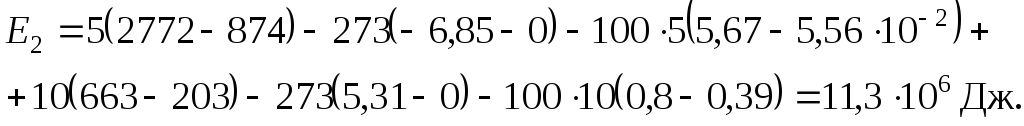
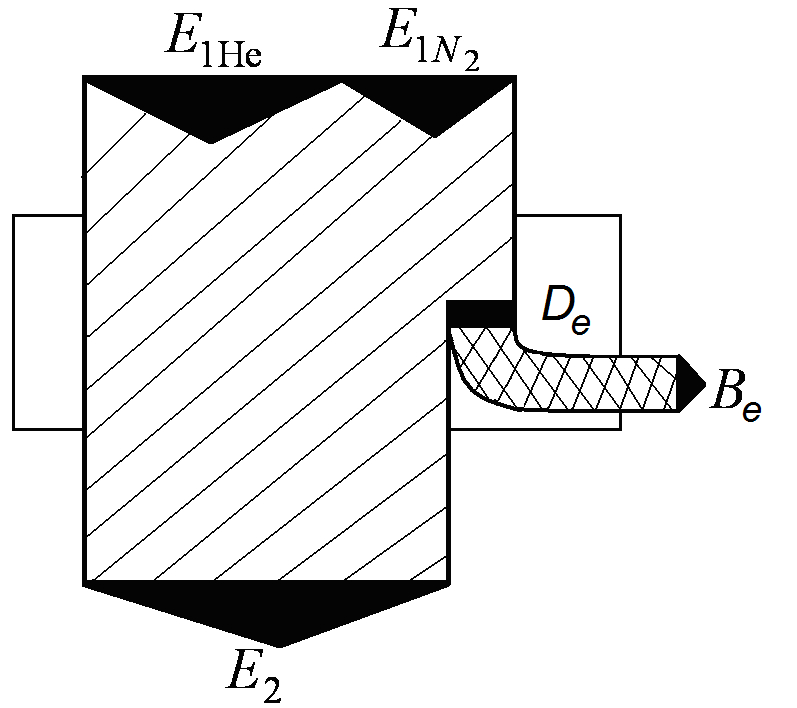
Рис. 2.4. Эксергическая диаграмма смешения газов
в постоянном объеме
Проверим правильность решения, рассчитав потери эксергии смешения и сравнив полученные значения с ранее рассчитанным результатом.
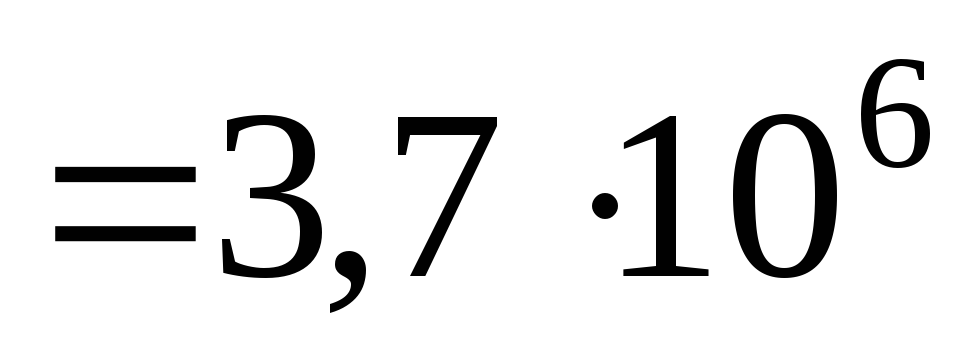 Дж.
Дж.
Сопоставим результаты
 ≈
≈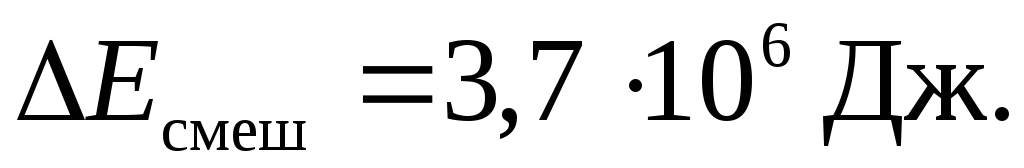
Полученная точность расчетов вполне удовлетворительна. По рассчитанным значениям построим эксергетическую диаграмму процесса смешения в объеме.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Сообщение от -=ЮрА=-
Во-первых каких газов?По условию в обоих перегородках азот
Во-вторых уже не будет газов из первой и 2-й перегородок, т.к. они станут единой равновесной системой.
Спасибо, кэп)
Сообщение от -=ЮрА=-
– по этому поводу имеется другой?
Только не заставляйте меня напрягаться с рисованием)
Сообщение от -=ЮрА=-
В третьих Причём тут парциальное давление, о нём можно было бы говорить если газы были разные например аргон и водород, метан и кислород, уже даже формулами показал что после адиабатной теплопередачи газ из перегородок станет одним целым
А ща про парциальное давление поговорим. Это давление газов смеси, это вы конечно знаете. Газ номер один – частицы азота из первой камеры, газ номер два – частицы азота из второй камеры. И по вашему графику следует, что в конце давление, которое будет оказывать частицы каждого из газов, будет равно друг другу – это есть неправда. Представьте в первой камере находится 1 частица, в другой – 10^23 частиц. По вашему графику следует, что когда будет равновесие, то одна частица будет оказываться такое же давление на стенки сосуда как 10^23 частиц. А правильный график это такой, где они не сойдутся в одну точку.
Сообщение от -=ЮрА=-
PS:KuKu, Не начинаем очередной холивор, предлагаю вдуматься в мои слова…
Да там я и не холиварил, можете если хотите, покажите хоть одну цитату в той теме, где я ошибался, с удовольствием о ней подумаю.
Сообщение от -=ЮрА=-
KuKu, если имеются свои соображения, ну как минимум надо привести выкладки,
Тут ручку даже брать лень, пишите уравнения Менделеева-Клайперона и уравнения адиабаты. Далее получаете столько же уравнений, сколько и неизвестных. Далее усиленно хлопаете в ладоши и радуетесь, что решили задачу.
Сообщение от -=ЮрА=-
утверждать же как paskal, что вконце концов став единой системой с давлением p3 азот и 1-й перегородки(с большим давлением) не изменил своей внутренней энергии которая пошла на расширение азота из второй перегородки просто глупо!В системе была работа вот только внешне на друге тела она никак не отразилась т.к. система изначально была замкнутой, вот и всё..
Открою вам страшную тайну … Он сказал, что в систему из вне не закачивают энергию и над системой внешние тела не совершают работу(перечитайте пост, где вам говорят про запятую) в остальные ваши перепалки не особо вчитывался, но думаю там тоже самое. Один про Фому, второй про Ерему.
Добавлено через 7 минут
По поводу графиков, может не так понял, что вы хотели написать. Поясните, что такое первая и вторая линия и тогда, если вы правы, думаю все разрешится.
Источник
Презентация на тему: ” Анализ и решение задачи по теме: «Явление осмоса в газах». Сосуд вместимостью 100л разделен полупроницаемой перегородкой на две равные части. В одной половине.” – Транскрипт:
1 Анализ и решение задачи по теме: «Явление осмоса в газах». Сосуд вместимостью 100л разделен полупроницаемой перегородкой на две равные части. В одной половине сосуда находиться водород массой 2г, в другой азот в количестве 1 моль. Определить давление по обе стороны от перегородки, если она может пропускать только водород. Температура в обоих половинах одинакова и равна 127ºС. Температура не меняется.
2 «Явление осмоса в газах» P 1 -? P 2 -? V=100·10 -3 м 3 m 1 = 2·10 -3 кг = 1моль T=( )K M 1 =2·10 -3 кг/моль T=( )K Подсказка 1 Подсказка2 Решение
3 «Явление осмоса в газах» Закон Дальтона Если в сосуде находится смесь газов, то каждый из них вносит свой вклад в общее давление. Парциальным давлением называют давление одного из газов при условии, что все остальные удалены из сосуда. Экспериментально установленный закон Дальтона утверждает : давление в смеси химически невзаимодействующих газов равно сумме их парциальных давлений P=P 1 +P 2 +…+P n При этом парциальное давление каждого из газов подчиняется в случае достаточно разреженных газов уравнению состояния идеального газа: где V – объем смеси, T – абсолютная температура, m 1 и m 2 – массы различных газов в смеси, а M 1 и M 2 – их молярные массы. Примером газовой смеси является воздух, состоящий из азота, кислорода, углекислого газа и других газов. Начало
4 «Явление осмоса в газах» Полупроницаемая мембрана Иллюстрацией закона Дальтона может служить процесс диффузии газа через полупроницаемую перегородку (мембрану). Пусть в начальный момент два разных газа занимают две половины сосуда, разделенные полупроницаемой мембраной. Температуры обоих газов и их начальные давления одинаковы. Мембрана полностью непроницаема для одного из газов и частично прозрачна для другого. В процессе диффузии газа через полупроницаемую перегородку давление в одной половине сосуда возрастает в соответствии с законом Дальтона, а в другой – падает. Это явление носит название осмоса. Начало
5 «Явление осмоса в газах» В начальный момент времени газы оказывают давление на стенки сосудов в соответствии с формулами: P 1 -? P 2 -? V=100·10 -3 м 3 m 1 = 2·10 -3 кг = 1моль T=( )K M 1 =2·10 -3 кг/моль
6 «Явление осмоса в газах» P 1 -? P 2 -? V=100·10 -3 м 3 m 1 = 2·10 -3 кг = 1моль T=( )K M 1 =2·10 -3 кг/моль После проникновения молекул водорода через мембрану и равномерное их распределение по всему объему давление в левом сосуде равно: Давление азота в правом сосуде:
7 «Явление осмоса в газах» P 1 -? P 2 -? V=100·10 -3 м 3 m 1 = 2·10 -3 кг = 1моль T=( )K M 1 =2·10 -3 кг/моль Таким образом в левом сосуде давление водорода равно: А в правом сосуде давление равно сумме парциальных давлений азота и водорода
Источник

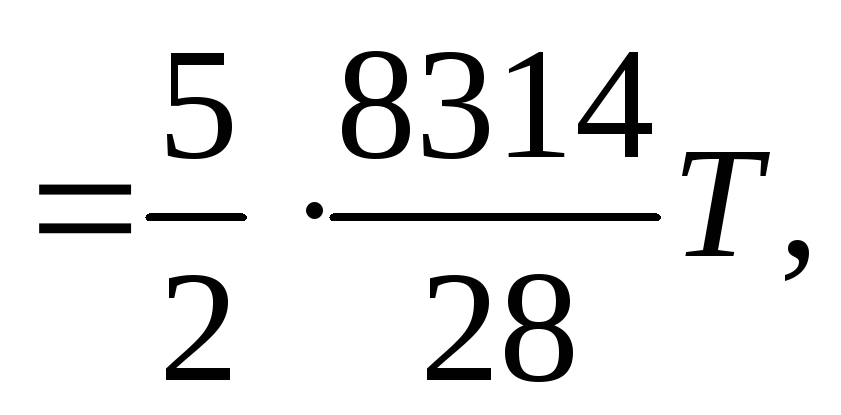 кДж/кг
кДж/кг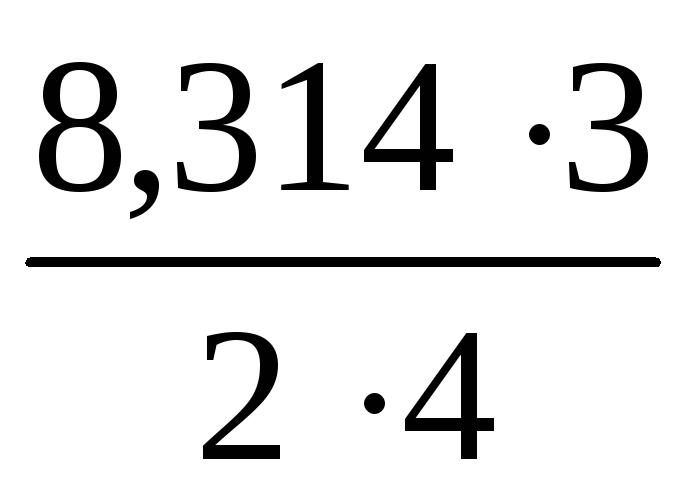 T, кДж/кг
T, кДж/кг giui
giui