Сосуд разделен адиабатной перегородкой на четыре части
МГТУ
им. Н. Э. Баумана
Домашнее
задание №1
по
термодинамике:
«Газовые
смеси»
Вариант
№15
Студент: Романов
А.С.
Группа: Э7-52
Преподаватель:
Чирков А.Ю.
-2012-
Условие
задания:
Сосуд
разделен адиабатной перегородкой на
четыре части, в каждой из которых
содержатся различные газы. После того
как перегородка убрана, происходит
«смешение в объеме» без теплообмена с
окружающей средой. Состояния газов до
смешения характеризуются следующими
параметрами: массой mi0,
кг; объемом Vi0,
м3;
температурой ti0,
˚С.
Необходимо
определить:
температуру
смеси после завершения процесса смешения
t;давление
смеси Р, МПа;газовую
постоянную R,
Дж/(кг*К);среднюю
молярную массу смеси µ, кг/моль;объемный
состав смеси {ri};молярный
состав смеси {ni};парциальное
давление компонентов смеси {pi},
МПа;приведенные
объемы компонентов смеси {Vi},
МПа;истинную
молярную теплоемкость смеси при р=const
для температуры смеси, которая
устанавливается после окончания
процессов смешения ср
,Дж/(кмоль*К);истинную
объемную теплоемкость смеси при р=const
после окончания процесса смешения C
, Дж/(м *К);истинную
массовую теплоемкость смеси при р=const
после окончания процесса смешения с,
Дж/(кг*К);количество
теплоты Q
(Дж), которое необходимо отвести от 3
кмоль смеси для охлаждения их при
р=const
до температуры смеси 300 К;количество
теплоты Q
(Дж), которое необходимо отвести от 4 м
смеси для охлаждения их при р=const
до температуры смеси 300 К;количество
теплоты Q
(Дж), которое необходимо отвести от 5
кг смеси для охлаждения их при р=const
до температуры смеси 300 К.
Исходные данные:
Газ | mi0, | Vi0, | ti0, |
O2 | 13 | 2,1 | 160 |
N2 | 16 | 1,6 | 260 |
H2 | 11 | 3,1 | 860 |
CO | 6 | 3,6 | 1060 |
Молярные
массы газов:
;
;
;
Решение:
При получении
значений из таблицы используется
линейная интерполяция:
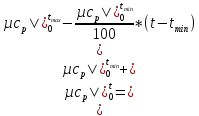 (1.1)
(1.1)
Температура
смеси после завершения процесса
смешения.
Нулевое приближение:
Первое приближение:
(1.2)
Вычислим
теплоемкости, входящие формулу (1.2),
необходимые для расчета суммарной
внутренней энергии газов до смешения,
а также температуры смеси в первом
приближении:
O2:
СО2:
SO2:
H2O:
Подставим полученные
значения:
кДж – суммарная
внутренняя энергия газов до смешения
(остаётся постоянной для всех последующих
приближений).
Второе
приближение:
(1.3)
Вычислим
теплоемкости, входящие формулу (1.3):
O2:
СО2
SO2:
H2O:
Подставим полученные
значения:
Третье
приближение:
(1.3)
Вычислим
теплоемкости, входящие формулу (1.3):
O2:
СО2
SO2:
H2O:
Подставим полученные
значения:
Принимаем:
Давление
смеси
,
МПа.
Для определения
давления используем формулу:
где
– масса смеси;
– объем смеси;
– газовая постоянная
смеси (см. пункт 3).
Тогда:
Постоянная
газовая смеси.
где
– массовая доля i-го
газа.
Тогда:
,
Средняя
молярная масса смеси –
.
Состав
смеси в объемных долях –
При одинаковых
температуре и давлении
всех газов одинаково, поэтому:
(см. пункт 6)
O2:
СО2:
SO2:
H2O:
Состав
смеси в молярных долях –
.
O2:
СО2:
SO2:
H2O:
Проверка:
,
верно.
Парциальные
давления компонентов смеси –
.
O2:
СО2:
SO2:
H2O:
Парциальные
объемы компонентов смеси –
.
O2:
СО2:
SO2:
H2O:
Истинная
молярная теплоемкость смеси при
,
установившеюся после смешения
.
O2:
СО2
SO2:
H2O:
Истинная
объемная теплоемкость смеси при
,
установившеюся после смешения
.
.
Истинная
массовая теплоемкость смеси при
,
установившеюся после смешения
.
.
Количество
теплоты, которое необходимо отвести
от 3 кмоль смеси для ее охлаждения приот температуры смеси до температуры
.
Определим среднюю
молярную теплоемкость смеси при процессе:
O2:
СО2
SO2:
H2O:
.
Кол-во
теплоты, которое необходимо отвести
от 4 м3 (н.
у.) смеси для ее охлаждения приот температуры смеси до температуры
.
Определим среднюю
объемную теплоемкость смеси при процессе:
.
.
Кол-во
теплоты, которое необходимо отвести
от 5кг смеси для ее охлаждения приот температуры смеси до температуры
.
Определим среднюю
массовую теплоемкость смеси при процессе:
Знак минус указывает
на то, что теплота отводится от смеси.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Срочно решить контрольную работу по физике из 6 задач в двух вариантах. Все решения нужно подробно расписать.
Фрагмент выполненной работы:
№ 2
Сосуд разделен адиабатными перегородками на четыре части, в каждой из которых содержатся различные газы. После того как перегородки убраны, без теплообмена с окружающей средой происходит образование горючей смеси. Состояние газов до смешения задано параметрами: масса mi, кг; объём Vi0, м3; температура t0, оС, одинаковая для всех газов. Данные находятся в таблице.
Требуется определить:
состав смеси в массовых долях;
исходные давления компонентов;
среднюю молярную массу смеси;
состав смеси в объёмных (мольных) долях;
парциальные объёмы компонентов;
давление смеси;
парциальные давления компонентов;
среднюю мольную теплоёмкость сv см при температуре t0;
количество тепла для изохорного нагрева смеси от t0 до t2.
Исходные данные:
№ варианта Газ mi, кг Vi0, м3 t0, 0С t2, 0С
е O2
N2
SO2
H2O 31
16
11
6 2,7
3,2
1,7
1,2 120 650
Решение:
1. (работа была выполнена специалистами Автор 24) Находим состав смеси в массовых долях
Определим массу смеси как сумму масс компонентов:
m=31+16+11+6=64 кг
Находим массовые доли компонентов по формуле:
gi=mim (1)
gO2=3164=0,484
gN2=1664=0,25
gSO2=1164=0,172
gH2O=664=0,094
Проверим правильность вычислений, найдя сумму долей:
gi=0,484+0,25+0,172+0,094=1
Сумма равна единице, доли вычислены верно.
2. Определим исходные давления компонентов.
Используем уравнения состояния газа:
pVT=mR (2)
где р – давление газа, Па
V – объем, м3;
m – масса, кг.
R – газовая постоянная, Дж/(кг∙К);
Давление компонента:
p=mRTV (3)
Выпишем значение газовых постоянных компонентов.
RO2=260 Дж/(кг∙К); RN2=297 Дж/(кг∙К);
RSO2=130 Дж/(кг∙К); RH2O=461 Дж/(кг∙К);
Абсолютная начальная температура:
T0=120+273=393 K
Вычисляем исходные давление компонентов по (3):
р0 O2=31∙260∙3932,7=1,17∙106 Па
р0 N2=16∙297∙3933,2=0,583∙106 Па
р0 SO2=11∙130∙3931,7=0,330∙106 Па
р0 H2O=6∙461∙3931,2=0,905∙106 Па
3. Находим среднюю молярную массу смеси.
Выпишем молекулярные массы компонентов смеси.
μО2=32 кг/кмоль; μN2=28 кг/кмоль;
μSO2=64 кг/кмоль; μH2O=18 кг/кмоль;
Средняя молярная масса смеси:
μсм=1i=1ngiμi=1gО2μО2+gN2μN2+gSO2μSO2+gH2OμH2O (4)
μсм=10,48432+0,2528+0,17264+0,09418=31,3 кг/кмоль
4. Находим состав смеси в объёмных (мольных) долях
Определим объем смеси как сумму объемов компонентов:
V=2,7+3,2+1,7+1,2=8,8 м3
Находим массовые доли компонентов по формуле:
ri=ViV (5)
rO2=2,78,8=0,307
rN2=3,28,8=0,364
rSO2=1,78,8=0,194
rH2O=1,28,8=0,136
Проверим правильность вычислений, найдя сумму долей:
ri=0,307+0,364+0,194+0,136=1
Сумма равна единице, доли вычислены верно.
5. Находим давление смеси.
Используем формулу (3).
Газовую постоянную R смеси ищем по формуле:
R=8314μсм
R=831431,3=265,6 Дж/(кг∙К)
p=64∙265,6∙3938,8=0,759∙106 Па
6. Находим парциальные давления компонентов.
Используем формулу:
pi=rip
рO2=0,307∙0,759=0,233∙106 Па
рN2=0,364∙0,759=0,276∙106 Па
рSO2=0,194∙0,759=0,147∙106 Па
рH2O=0,136∙0,759=0,103∙106 Па
7…
Посмотреть предложения по расчету стоимости
Зарегистрируйся, чтобы получить больше информации по этой работе
Источник
Сообщение от -=ЮрА=-
Во-первых каких газов?По условию в обоих перегородках азот
Во-вторых уже не будет газов из первой и 2-й перегородок, т.к. они станут единой равновесной системой.
Спасибо, кэп)
Сообщение от -=ЮрА=-
– по этому поводу имеется другой?
Только не заставляйте меня напрягаться с рисованием)
Сообщение от -=ЮрА=-
В третьих Причём тут парциальное давление, о нём можно было бы говорить если газы были разные например аргон и водород, метан и кислород, уже даже формулами показал что после адиабатной теплопередачи газ из перегородок станет одним целым
А ща про парциальное давление поговорим. Это давление газов смеси, это вы конечно знаете. Газ номер один – частицы азота из первой камеры, газ номер два – частицы азота из второй камеры. И по вашему графику следует, что в конце давление, которое будет оказывать частицы каждого из газов, будет равно друг другу – это есть неправда. Представьте в первой камере находится 1 частица, в другой – 10^23 частиц. По вашему графику следует, что когда будет равновесие, то одна частица будет оказываться такое же давление на стенки сосуда как 10^23 частиц. А правильный график это такой, где они не сойдутся в одну точку.
Сообщение от -=ЮрА=-
PS:KuKu, Не начинаем очередной холивор, предлагаю вдуматься в мои слова…
Да там я и не холиварил, можете если хотите, покажите хоть одну цитату в той теме, где я ошибался, с удовольствием о ней подумаю.
Сообщение от -=ЮрА=-
KuKu, если имеются свои соображения, ну как минимум надо привести выкладки,
Тут ручку даже брать лень, пишите уравнения Менделеева-Клайперона и уравнения адиабаты. Далее получаете столько же уравнений, сколько и неизвестных. Далее усиленно хлопаете в ладоши и радуетесь, что решили задачу.
Сообщение от -=ЮрА=-
утверждать же как paskal, что вконце концов став единой системой с давлением p3 азот и 1-й перегородки(с большим давлением) не изменил своей внутренней энергии которая пошла на расширение азота из второй перегородки просто глупо!В системе была работа вот только внешне на друге тела она никак не отразилась т.к. система изначально была замкнутой, вот и всё..
Открою вам страшную тайну … Он сказал, что в систему из вне не закачивают энергию и над системой внешние тела не совершают работу(перечитайте пост, где вам говорят про запятую) в остальные ваши перепалки не особо вчитывался, но думаю там тоже самое. Один про Фому, второй про Ерему.
Добавлено через 7 минут
По поводу графиков, может не так понял, что вы хотели написать. Поясните, что такое первая и вторая линия и тогда, если вы правы, думаю все разрешится.
Источник
Презентация на тему: ” Анализ и решение задачи по теме: «Явление осмоса в газах». Сосуд вместимостью 100л разделен полупроницаемой перегородкой на две равные части. В одной половине.” — Транскрипт:
1
Анализ и решение задачи по теме: «Явление осмоса в газах». Сосуд вместимостью 100л разделен полупроницаемой перегородкой на две равные части. В одной половине сосуда находиться водород массой 2г, в другой азот в количестве 1 моль. Определить давление по обе стороны от перегородки, если она может пропускать только водород. Температура в обоих половинах одинакова и равна 127ºС. Температура не меняется.
2
«Явление осмоса в газах» P 1 -? P 2 -? V=100·10 -3 м 3 m 1 = 2·10 -3 кг = 1моль T=( )K M 1 =2·10 -3 кг/моль T=( )K Подсказка 1 Подсказка2 Решение
3
«Явление осмоса в газах» Закон Дальтона Если в сосуде находится смесь газов, то каждый из них вносит свой вклад в общее давление. Парциальным давлением называют давление одного из газов при условии, что все остальные удалены из сосуда. Экспериментально установленный закон Дальтона утверждает : давление в смеси химически невзаимодействующих газов равно сумме их парциальных давлений P=P 1 +P 2 +…+P n При этом парциальное давление каждого из газов подчиняется в случае достаточно разреженных газов уравнению состояния идеального газа: где V – объем смеси, T – абсолютная температура, m 1 и m 2 – массы различных газов в смеси, а M 1 и M 2 – их молярные массы. Примером газовой смеси является воздух, состоящий из азота, кислорода, углекислого газа и других газов. Начало
4
«Явление осмоса в газах» Полупроницаемая мембрана Иллюстрацией закона Дальтона может служить процесс диффузии газа через полупроницаемую перегородку (мембрану). Пусть в начальный момент два разных газа занимают две половины сосуда, разделенные полупроницаемой мембраной. Температуры обоих газов и их начальные давления одинаковы. Мембрана полностью непроницаема для одного из газов и частично прозрачна для другого. В процессе диффузии газа через полупроницаемую перегородку давление в одной половине сосуда возрастает в соответствии с законом Дальтона, а в другой – падает. Это явление носит название осмоса. Начало
5
«Явление осмоса в газах» В начальный момент времени газы оказывают давление на стенки сосудов в соответствии с формулами: P 1 -? P 2 -? V=100·10 -3 м 3 m 1 = 2·10 -3 кг = 1моль T=( )K M 1 =2·10 -3 кг/моль
6
«Явление осмоса в газах» P 1 -? P 2 -? V=100·10 -3 м 3 m 1 = 2·10 -3 кг = 1моль T=( )K M 1 =2·10 -3 кг/моль После проникновения молекул водорода через мембрану и равномерное их распределение по всему объему давление в левом сосуде равно: Давление азота в правом сосуде:
7
«Явление осмоса в газах» P 1 -? P 2 -? V=100·10 -3 м 3 m 1 = 2·10 -3 кг = 1моль T=( )K M 1 =2·10 -3 кг/моль Таким образом в левом сосуде давление водорода равно: А в правом сосуде давление равно сумме парциальных давлений азота и водорода
Источник
2017-10-05
Сосуд с разреженным газом разделен на две части тонкой перегородкой, в которой имеется отверстие, размер которого мал по сравнению со средней длиной свободного пробега (рис. 1). Найти отношение концентрации газа в разных частях сосуда, если в одной из них поддерживается температура $T_{1}$, в другой $T_{2}$.

Решение:
Будем считать, что газ в сосуде идеальный, т. е. его молекулы взаимодействуют между собой только при столкновениях. По условию задачи газ разрежен настолько, что средняя длина свободного пробега молекул между столкновениями много больше размеров отверстия. В этом случае молекулы свободно проходят через отверстие, причем каждая молекула приходит в другую половину сосуда с той же энергией, которой она обладала до этого. Средняя энергия молекул при термодинамическом равновесии определяется температурой. Поэтому переход молекул из одной части сосуда в другую должен приводить к выравниванию температур.
Говорить об определенной температуре газа каждой части сосуда можно только в том случае, когда отверстие в перегородке достаточно маленькое, так что установление термодинамического равновесия в каждой части сосуда происходит гораздо быстрее, чем выравнивание температур этих частей.
Сколько же молекул проходит в единицу времени через отверстие из одной половины сосуда в другую? Нетрудно сообразить, что среднее число таких молекул $N$ пропорционально концентрации $n$ и средней скорости $langle v rangle$ молекул в той половине сосуда, из которой они переходят, а также площади отверстия $S$:
$N = Cn langle v rangle S$. (1)
Для вычисления числового значения безразмерного коэффициента $C$ нужно знать закон распределения молекул по направлениям скорости. Однако для решения этой задачи значение $C$ нам не потребуется.
В стационарном состоянии полное число молекул в каждой половине сосуда не меняется со временем. Поэтому среднее число молекул, проходящих через отверстие слева направо и справа налево, должно быть одинаковым. Отсюда с помощью соотношения (1) получаем
$n_{1} langle v_{1} rangle = n_{2} langle v_{2} rangle$. (2)
Средние скорости молекул в каждой половине пропорциональны квадратному корню из соответствующей температуры. Поэтому из равенства (2) находим
$n_{1}/n_{2} = sqrt{T_{2}/T_{1}}$. (3)
В горячей части сосуда концентрация молекул меньше. Однако давление газа там больше, чем в холодной части. Учитывая, что давление выражается формулой $p = nkT$, с помощью равенства (3) получаем для отношения давлений в разных половинах сосуда
$p_{1}/p_{2} = sqrt{T_{1}/T_{2}}$. (4)

рис.2
Рассмотренные в этой задаче закономерности, связанные с прохождением молекул газа через отверстие, соединяющее сосуды с разной температурой, позволяют объяснить следующий простой, но очень эффектный опыт. Керамический сосуд с пористыми стенками опускается открытым концом в воду (рис. 2). Внутри сосуда находится спираль, при пропускании тока через которую можно нагревать находящийся в сосуде воздух. При включении спирали температура воздуха повышается, он расширяется и начинает выходить пузырями из находящегося подводой отверстия сосуда. При достижении стационарного состояния , когда подводимая спиралью теплота станет равной теплоте, отдаваемой поверхностью сосуда в окружающую среду, в сосуде установится определенная температура. Казалось бы, что при этом выход пузырей воздуха должен прекратиться. Так бы и произошло, если бы стенки сосуда были непроницаемыми для молекул воздуха, например стеклянными или металлическими.
Но если стенки сосуда пористые, то пузырьки воздуха будут выходить все время, даже тогда, когда температура воздуха в сосуде перестанет повышаться! В чем же здесь дело?
Температура воздуха внутри пористого сосуда выше, чем снаружи, в атмосфере. Давление же воздуха там и там практически одинаково: внутри сосуда оно больше атмосферного всего на несколько сантиметров водяного столба, что соответствует глубине погружения отверстия сосуда код воду. Через поры в стенках сосуда происходит непрерывный обмен молекулами между воздухом внутри сосуда и в атмосфере, так же как это происходит в сосуде с отверстием в перегородке, рассмотренным в данной задаче. В замкнутом сосуде в стационарном состоянии число молекул, проходящих через отверстие в обе стороны, одинаково. В результате, как видно из формулы (3), в частях сосуда устанавливались такие концентрации, что произведение концентрации на корень из термодинамической температуры было одинаково: $n sqrt{T} = const$.
В рассматриваемом случае одинаковыми по обе стороны пористой перегородки будут давления воздуха. Так как $p = nkT$, то теперь $nT = const$. Но это означает, что потоки молекул воздуха через поры в стенках из атмосферы в сосуд и обратно неодинаковы. Какой же из них больше? Так как поток молекул пропорционален произведению $n sqrt{T}$ в той части, откуда он идет, то при выполнении условия $nT = const$ он будет больше оттуда, где температура ниже. Это и дает объяснение описанному опыту: поток воздуха через поры внутрь сосуда больше, чем наружу. В результате в стационарном состоянии входящий через поры в сосуд избыточный воздух нагревается, расширяется и выходит в виде пузырей через отверстие.
Источник
