Сосуд разделен перегородкой на две части объемы которых равны
Задача по физике – 14089
Сосуд разделен перегородкой на две равные части объемом $V$ каждая. В одной части находится азот, а в другой кислород при одинаковых давлениях $P$ и температурах $T$. Газы в сосуде сильно разрежены (средняя длина свободного пробега велика по сравнению с размерами сосуда). В момент $t = 0$ в перегородке открывается небольшое отверстие площади $S$. Найти давление в обеих частях сосуда в зависимости от времени. Температуру газа во все время процесса считать неизменной. Результат выразить через средние скорости молекул азота и кислорода $bar{v}_{a}$ и $bar{v}_{к}$.
Подробнее
Задача по физике – 14090
Полностью эвакуированный герметический сосуд помещен в атмосферу, состоящую из смеси двух газов, молекулярные массы которых относятся как 1 : 4, а отношение концентраций (т. е. чисел молекул в единице объема) равно $alpha$. Смесь газов вне сосуда поддерживается при постоянных давлении и температуре. В стенке сосуда оказалось малое отверстие, через которое оба газа стали очень медленно натекать в сосуд. Определить максимальное и минимальное значения отношения концентраций легкой и тяжелой компонент газовой смеси в сосуде и моменты времени, когда достигаются эти значения.
Подробнее
Задача по физике – 14091
Тонкостенный сосуд объема $V$, наполненный идеальным газом, поддерживается при постоянной температуре $T$. В стенке сосуда имеется маленькое отверстие площади $S$, через которое молекулы газа вылетают в вакуум. Какое количество тепла $Q = Q(t)$ надо подводить к сосуду в единицу времени для поддержания в нем постоянной температуры?
Подробнее
Задача по физике – 14092
Вольфрамовая нить, испаряясь в высокий вакуум при температуре $T = 2000 К$, уменьшается в массе, как показали измерения, со скоростью $q = 1,14 cdot 10^{-13} г/(с cdot см^{2})$. Вычислить давление насыщенного пара вольфрама при этой температуре.
Подробнее
Задача по физике – 14093
Идеально упругий шарик движется вверх и вниз в поле силы тяжести, отражаясь от пола по законам упругого удара. Найти связь между его средними по времени значениями кинетической и потенциальной энергий. Результат использовать для установления связи между средними значениями кинетической и потенциальной энергий молекулы воздуха в поле земного тяготения. Пользуясь этим результатом, получить формулу для разности молярных теплоемкостей $C_{P} – C_{V}$.
Подробнее
Задача по физике – 14094
Доказать, что гравитационное поле планеты не может удерживать неограниченно долго планетную атмосферу. Последняя должна рассеяться в окружающее пространство.
Подробнее
Задача по физике – 14095
Скорость рассеяния планетной атмосферы в мировое пространство можно характеризовать временем рассеяния атмосферы $tau$. Так называют время, по истечении которого число частиц в атмосфере убывает в $e$ раз. Оценить время рассеяния планетной атмосферы $tau$, предполагая, что атмосфера изотермическая и состоит из одинаковых частиц. Атмосферу считать бесконечно разреженной. В этих условиях взаимными столкновениями молекул можно пренебречь – максвелловское распределение скоростей устанавливается в результате столкновений молекул с поверхностью планеты. Молекулы выбывают из атмосферы и улетают в межпланетное пространство, если в результате столкновений с поверхностью планеты они получают скорости, превышающие вторую космическую скорость. (В проблеме рассеяния планетных атмосфер вторая космическая скорость называется скоростью убегания $v_{уб}$.) Найти время $tau$ для атомарного и молекулярного водорода земной атмосферы, предполагая, что температура последней $T = 300 К$.
Подробнее
Задача по физике – 14096
По одной из старых теорий (Гельмгольц, 1854 г.; лорд Кельвин, 1861 г.) солнечное излучение поддерживается за счет тепла, образующегося при сжатии Солнца. Предполагая, что Солнце представляет собой однородный шар, плотность вещества которого на любых расстояниях от центра одна и та же, подсчитать, какое количество тепла $Q$ образуется, если радиус Солнца уменьшится от $R_{1}$ до $R_{2}$. На сколько лет хватит выделившегося тепла, если предположить, что интенсивность солнечного излучения постоянна во времени и если радиус Солнца уменьшится на 1/10 своей первоначальной величины ($R_{2} = 0,9R_{1}$)? Масса Солнца $M = 2 cdot 10^{33} г$, средний радиус $R_{1} = 6,95 cdot 10^{10} см$, гравитационная постоянная $G = 6,67 cdot 10^{-8} дин cdot см^{2}/г^{2}$, солнечная постоянная $A = 1,39 cdot 10^{6} эрг/(с cdot см^{2})$, среднее расстояние Земли от Солнца $1,5 cdot 10^{13} см$. Оценить также, насколько повысилась бы температура Солнца, если бы сжатие произошло внезапно. Теплоемкость солнечного вещества можно грубо оценить, предполагая, что Солнце целиком состоит из водорода. (Это дает завышенное значение для теплоемкости. По современным данным масса Солнца состоит приблизительно на 70-80% из водорода.)
Подробнее
Задача по физике – 14097
По классической теории молярная теплоемость водорода $C = frac{5}{2} R$. Какие отклонения от этого значения нужно ожидать при достаточно низких температурах?
Подробнее
Задача по физике – 14098
Вычислить по квантовой теории молярные теплоемкости $C_{V}$ и $C_{P}$ углекислого газа $CO_{2}$ при $0^{ circ} С$. Молекула $CO_{2}$ является линейной ($O-C-O$), т. е. три атома, из которых она состоит (точнее, их положения равновесия), расположены на одной прямой. Момент инерции молекулы $I = 7,2 cdot 10^{-39} г cdot см^{2}$. Частоты нормальных колебаний молекулы по спектроскопическим данным: $tilde{ nu}_{1} = bar{ nu}_{2} = 667,3 см^{-1}, tilde{ nu}_{3} = 1388,3 см^{-1}, tilde{ nu}_{4} = 2349,3 см^{-1}$. Частотам $tilde{ nu}_{1}$ и $tilde{ nu}_{2}$ соответствуют поперечные колебания, совершающиеся во взаимно перпендикулярных плоскостях; частоте $tilde{ nu}_{3}$ – продольные колебания, в которых атомы кислорода колеблются синфазно; частоте $tilde{ nu}_{4}$ – также продольные колебания, нов них атомы кислорода колеблются в противоположных фазах (рис.).
Примечание. Под $tilde{ nu}$ здесь понимается так называемая спектроскопическая частота, т. е. $tilde{ nu} = frac{1}{ lambda}$, где $lambda$ – длина волны. Величина $tilde{ nu}$ связана с обычной частотой $nu$ соотношением $nu = c tilde{ nu}$, где $c$ – скорость света.
Подробнее
Задача по физике – 14099
Пусть $F$ – какая-либо аддитивная физическая величина, характеризующая систему $N$ молекул идеального газа, так что $F = sum f_{i}$ где величины $f_{i}$ характеризуют $i$-ю молекулу того же газа. Выразить средний квадрат флуктуации величины $F$ через средний квадрат флуктуации величины $f$, а также найти относительную флуктуацию той же величины.
Подробнее
Задача по физике – 14100
В закрытом сосуде объема $V$ в отсутствие силовых полей находятся N молекул идеального газа. Определить среднее число молекул и его флуктуации в объеме $v$, являющемся малой частью объема $V$.
Подробнее
Задача по физике – 14101
Сосуд с $N$ молекулами идеального газа разделен перегородкой на две части с объемами $V_{1}$ и $V_{2}$. Найти вероятность того, что в первой части будет содержаться $N_{1}$ а во второй $N_{2}$ молекул.
Подробнее
Задача по физике – 14102
Два одинаковых сосуда, в которых находится по молю одного и того же идеального газа при одинаковых условиях, сообщаются между собой через отверстие. Какое число молекул $n$ должно перейти из одного сосуда в другой, чтобы возникшее состояние стало в $alpha = e$ раз менее вероятным, чем исходное?
Подробнее
Задача по физике – 14103
Решить задачу 14102, используя формулу Больцмана $S = k ln P$ и термодинамическое выражение для энтропии идеального газа. Сравнить результат с предыдущим решением и объяснить расхождение.
Подробнее
Источник
1. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой 200 кг? Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
2. Воздушный шар объемом 2500 м3 с массой оболочки 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Рассчитайте максимальную массу груза, который может поднять шар, если воздух в нем нагреть до температуры 77°С. Температура окружающего воздуха 7°С, его плотность 1,2 кг/м3. Оболочку шара считать нерастяжимой. (Решение)
3.
Воздушный шар объемом 2500 м3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха 7°С, а его плотность 1,2 кг/м3, то при нагревании воздуха в шаре до температуры 77°С шар поднимает груз с максимальной массой 200 кг. Какова масса оболочки шара? Оболочку шара считать нерастяжимой. (Решение)
4.
Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
5.
Воздушный шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием. Он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па, груз массой 225 кг. Какова масса гелия в оболочке шара? Считать, что оболочка шара не оказывает сопротивления изменению объема шара. (Решение)
6. При исследовании уравнения состояния газа ученик соединил сосуд (1) объемом 150 мл с манометром (2) тонкой трубкой и опустил сосуд в горячую воду (см. рисунок). Чему равна плотность воздуха в сосуде? Начальные показания манометра равны 0 мм рт. ст. Шкала манометра и нижняя шкала барометра (3) проградуированы в мм рт. ст. Верхняя шкала барометра проградуирована в кПа. Объем измерительного механизма манометра и соединительной трубки значительно меньше 150 мл. (Решение)
7. Теплоизолированный сосуд объемом V = 2 м3 разделен пористой неподвижной перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона — нет. В начальный момент в одной части сосуда находится νHe = 2 моль гелия, а в другой — νAr = 1 моль аргона. Температура гелия TНe = 300 К, а температура аргона ТAr = 600 К. Определите температуру гелия после установления равновесия в системе. (Решение)
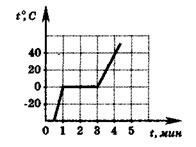
8. На рисунке представлен график изменения температуры вещества в калориметре с течением времени. Теплоемкостью калориметра и тепловыми потерями можно пренебречь и считать, что подводимая к сосуду мощность постоянна. Рассчитайте удельную теплоемкость вещества в жидком состоянии. Удельная теплота плавления вещества равна 100 кДж/кг. В начальный момент времени вещество находилось в твердом состоянии. (Решение)
9. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом масса
пара в сосуде? Ответ поясните.
(Решение)
10. В цилиндрическом сосуде под поршнем длительное время находятся вода
и ее пар. Поршень начинают вдвигать в сосуд. При этом температура
воды и пара остается неизменной. Как будет меняться при этом
отношение массы пара к массе жидкости в сосуде? Ответ поясните. (Решение)
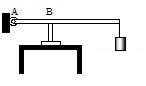11. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину стержня, если его можно считать невесомым.
(Решение)
12. В цилиндр объемом 0,5 м3 насосом закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А (см. рисунок к зад. 11). К свободному концу стержня подвешен груз массой 2 кг. Клапан открывается через 580 с работы насоса, если в начальный момент времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном отверстия 5·10-4 м2, расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите длину AB. (Решение)
13. Воздушный шар имеет газонепроницаемую оболочку массой 400 кг и содержит 100 кг гелия. Какой груз он может удерживать в воздухе на высоте, где температура воздуха 17°С, а давление 105 Па? Считать, что оболочка шара не оказывает сопротивления изменению объема шара.
(Решение)
14. Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м3, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t0 = 0°C. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.
(Решение)
15. В высоком вертикальном цилиндрическом сосуде под тяжелым поршнем, способным перемещаться вдоль стенок сосуда практически без трения, находится некоторое количество воздуха под давлением p = 1,5 атм. Поршень находится в равновесии на высоте H1 = 20 см над дном сосуда. Определите, на какое расстояние ΔH сместится поршень, если сосуд перевернуть открытым концом вниз и дождаться установления равновесия. Считать температуру воздуха и атмосферное давление p0 = 1 атм постоянными. Массой воздуха в сосуде по сравнению с массой поршня можно пренебречь.
(Решение)
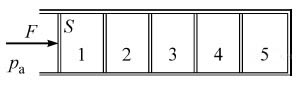16. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 100 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 2 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Какого значения достигнет F, когда объём газа в самом правом, 5-м отсеке цилиндра уменьшится в n = 2 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
17. Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению pа = 105 Па окружающей цилиндр атмосферы (см. рисунок к зад 16). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения Fтр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. Когда давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.
(Решение)
18. Газ в цилиндрическом сосуде разделен на две равные части подвижным поршнем, имеющим массу m и площадь сечения S. При горизонтальном положении цилиндра давление газа в каждой половине сосуда равно p. Определить давление p1 газа над поршнем при вертикальном положении цилиндра. Температуру газа считать постоянной.
(Решение)
19. Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу 1 кг. Шар наполняют гелием при атмосферном давлении 105 Па. Определите минимальную массу оболочки, при которой шар начнет поднимать сам себя. Температура гелия и окружающего воздуха одинакова и равна 0°С. (Площадь сферы S= 4πr2, объем шара V = 4/3πr3.)
(Решение)
20. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Площадь поперечного сечения поршня S = 30 см2. Давление окружающего воздуха p = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. Какое количество теплоты нужно отвести от газа при его медленном охлаждении, чтобы поршень передвинулся на расстояние х = 10 см?
(Решение)
21. В горизонтальном цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный идеальный газ. Давление окружающего воздуха р = 105 Па. Трение между поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения от газа отведено количество теплоты |Q| = 75 Дж. При этом поршень передвинулся на расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?
(Решение)
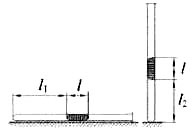22. В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23.8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст.
(Решение)
23. В водонепроницаемым мешок, лежащий на дне моря на глубине 73,1 м. закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и. когда объём воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикреплённым к нему грузом массой 25,0 тонн. Определите массу воздуха в мешке в момент начала его всплывания. Температура воды раина 7°С. атмосферное давление па уровне моря равно 105 Па. Объёмом груза и стенок мешка пренебречь. Масса оболочки мешка неизвестна.
(Решение)
24. Сосуд разделен тонкой перегородкой на две части, отношение объёмов у которых V2/V1 = 3. В первой и второй частях сосуда находится воздух с относительной влажностью соответственно φ1 = 60% и φ2 = 70%. Какой будет влажность воздуха в сосуде, если перегородку убрать? Считать, что температура воздуха постоянна.(Решение)
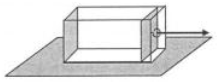25. В металлическом сосуде под поршнем находится воздух при атмосферном давлении (см. рисунок). Сосуд имеет массу 10 кг и расположен в горизонтальном положении на поверхности стола. Поршень может скользить без трения со стенками сосуда. Массон поршня и воздуха, заключённого в сосуде, можно пренебречь. За привязанный к нему шнур поршень очень медленно тянут в горизонтальном направлении. На сколько процентов возрастёт объём воздуха под поршнем к моменту, когда сосуд начнёт скользить по столу? Коэффициент трения покоя между сосудом и поверхностью стола равен 0,5. Площадь дна поршня 105 см2. Атмосферное давление 105 Па.
(Решение)
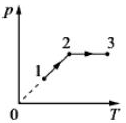26.Один моль одноатомного идеального газа совершает процесс 1-2-3, график которого показан на рисунке в координатах р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К?
(Решение)
27. Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К,. а аргона – 900 К. Объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемешается без трения? Теплоёмкостью цилиндра н поршня пренебречь.
(Решение)
Источник